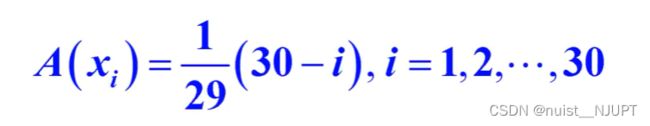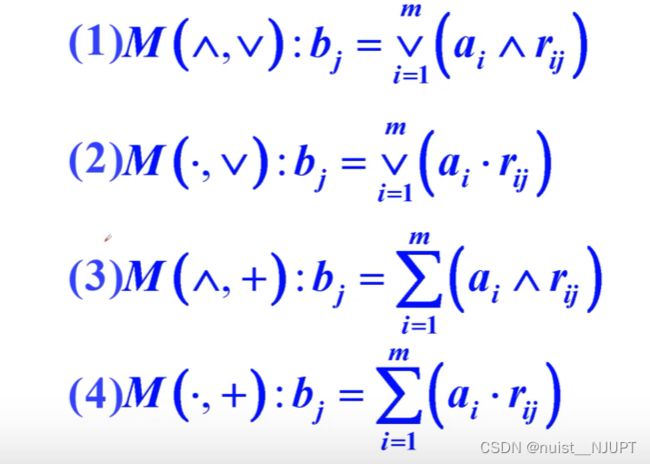备战数学建模12-模糊综合评价模型

目录

一、概述

1-数学归纳法与秃子悖论

2-数学中研究量的划分

3-生活中处处的存在模糊性(和确定性相对应)

4-模糊数学的概念

二、经典集合和模糊集合的基本概念

1-经典集合和特征函数

2-模糊集合和隶属函数

三、隶属函数的构建与模糊集的运算

1-隶属函数的确定

2-模糊集的运算

四、模糊综合评价的应用

1-模糊综合评价的方法和步骤

2-模糊综合评价的MATLAB编程实现

---

一、概述

1-数学归纳法与秃子悖论

先思考一下数学归纳法：假设n=1,问题成立，再假设n=k时问题成立，那么只需验证n=k+1时，问题成立，则可以得出结论：对于所有的n，问题均成立。

我们再看一下秃子悖论，假设博主满头秀发。

首先减少一根，那么博主肯定不是秃子，假设减少k根博主也不是秃子，那么根据数学归纳法，减少k+1根博主不是秃子的话，则得出结论减少n根博主都不是秃子。

这样的话：就变成了光头也不是秃子。

从文学上解释：压死骆驼的最后一根稻草。

从哲学上解释：量变引起质变。

从数学上解释：就是模糊的概念。

2-数学中研究量的划分

对于量划分为确定性的量和不确定性的量。

确定性的量：经典代数，比如几何，数学。

不确定性的量：概率论，随机过程，灰色系统，模糊数学。

3-生活中处处的存在模糊性(和确定性相对应)

确定性的：性别，年龄，天气，身高，体重等等

模糊性的：帅，美，白，高等等

4-模糊数学的概念

模糊数学又称fuzzy数学，1956美国控制论专家扎德发表了一篇论文'Fuzzy sets'，标志着模糊数学的诞生。

二、经典集合和模糊集合的基本概念

1-经典集合和特征函数

集合：具有相同属性事务的集体，例如：颜色，性别，手机品牌。

集合的基本属性：互斥性：集合中任意两个元素不相等，确定性：属于和不属于只能发生一个。

数学中经典函数的刻画：特征函数。

fA作用于U上面，把U中的每一个元素映射到集合中，

2-模糊集合和隶属函数

模糊集合的隶属函数如下所示，A是年轻，但是年轻是个概念，具体多少岁属于年轻呢？

给定论域U，所谓U上的一个模糊集A是指对于任意一个x属于U，都能找到一个正数UA，

给出了一个隶属函数UA属度介于0和1，UA的值称为x对A的隶属度，隶属度越大表述越是属于这个集合。每个元素都有隶属度的集合即为模糊集，确定模糊集的关键是构造隶属函数。

三、隶属函数的构建与模糊集的运算

1-隶属函数的确定

由模糊集的概念可知，模糊数学的基本思想是隶属度，所以应用模糊数学方法建立数学模型的关键是建立符合实际的隶属函数，然而如何确定一个模糊集的隶属函数至今还是尚未解决的问题。

确定隶属度的常用方法是模糊分布法。

下面看一下常用的模糊分布：

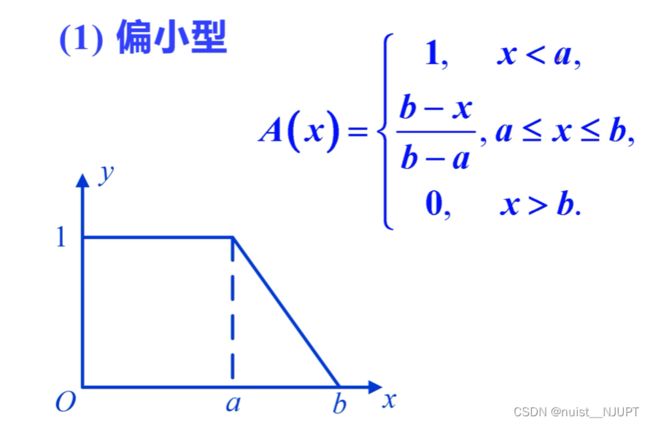
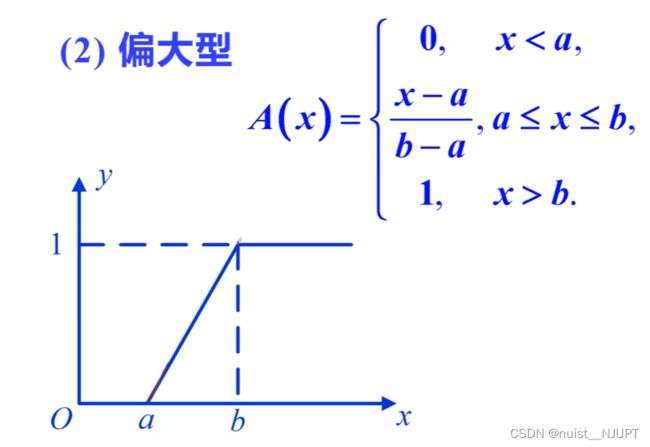
第一种是偏小型：xb的时候，隶属函数为0.

 第二种偏大型，和偏小性相反，具体如下：

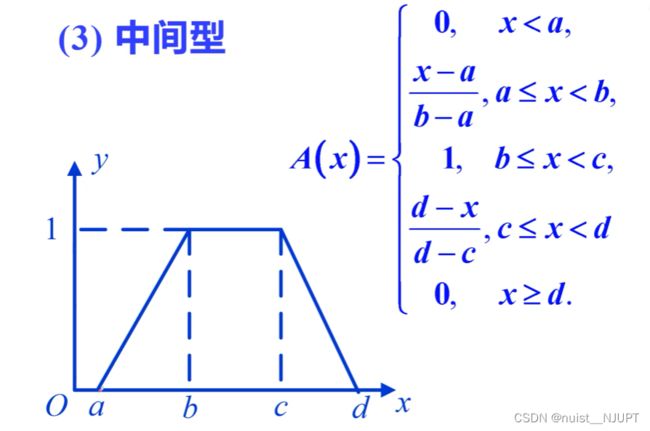
第三种是中间型：一个梯形计算，具体如下所示：

我们看一下上面的例子1，对隶属函数的确定，具体如下：

我们发现长就是一个模糊的概念，到底多长是属于长呢？我们可以使用模糊集来表示：

 若A为长线段的集合，则线段xi作为集合A的成员资格，就是xi对A的隶属度。

下面建立A的一种隶属函数，因为线段越长，属于A的程度越大，所以线段的长短可以作为A的隶属度。

我们令A(1)=1,A(30)=0,可以作直线：

 从而得到第i条线段xi属于长线段集合A的隶属函数：

2-模糊集的运算

由于模糊集中没有元素和集合间的绝对隶属关系，所以模糊集的运算是通过隶属函数完成的。

 

还有并，交，补，内积等 运算。

四、模糊综合评价的应用

1-模糊综合评价的方法和步骤

综合评价的方法很多，常用的有：灰色评价法，模糊综合评价法，层次分析法，数据包络分析法，人工神经网络分析法，理想解法等等，有时候还可以两种或者多种评价方法的组合。

第1步：确定评级指标和评价等级

这里m是评价因素的个数，通常由具体指标体系决定，n为评语个数，一般划分3-5个等级。

 

 第2步：构造模糊综合评价矩阵

模糊评价矩阵R中每行元素的和为1.

 

 

 第3步：评价指标权重的确定

 尽量不要使用主观法，使用客观法确定权重系数更好，最好使用变异系数法。

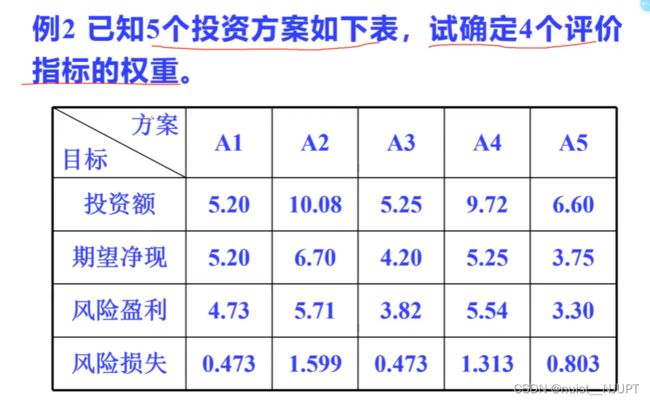
 我们看一下使用变异系数法确定如下指标的权重，例子2具体如下：

 在确定权重之前我们可以先学习一下变异系数法的基本原理，具体如下：

方差是反应数据分辨能力的重要因素。

 指标的分辨能力定义为：标准差除以均值的绝对值，具体如下：

 上述例子2的具体解法如下：

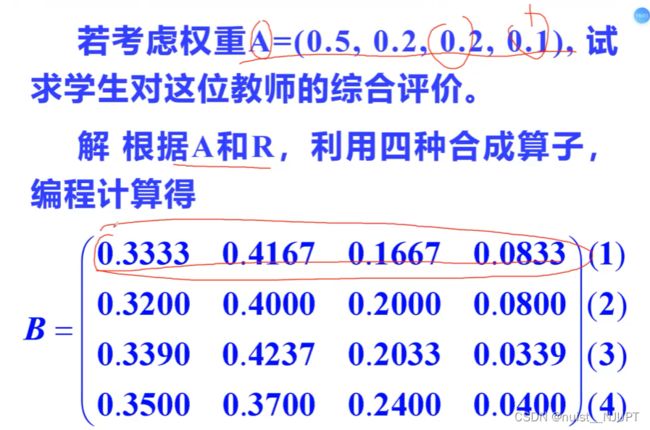
计算结果如下所示：

第4步：模糊合成和综合评价

 

评价矩阵R和权向量A的合成不是简单的相乘，常用的合成方法有如下几种：

 

 

 我们看一下下面的例子3，感受一下： 

 比如第一种方案计算出的分别为0.4，0.5，0.2，0.1.通过分别除以1.2得到第一行的结果。

 

 我们学习一下相对偏差模糊矩阵评价法，具体如下：6.

 相对偏差评价法具体的步骤如下所示：

（1）虚拟理想方案

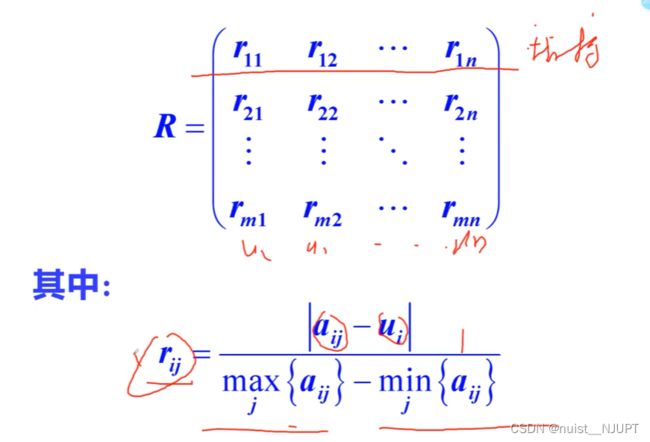
（2） 建立相对偏差模糊矩阵R

R中行代表指标，列代表评价集

 相对偏差法得到的值越小越好。

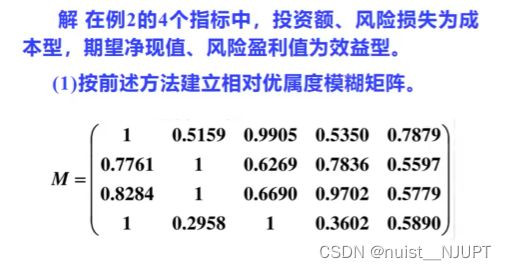
接下来我们学习另外一种，相对优属度模糊矩阵评价法，具体如下：

 相对优属度评价法的步骤如下：

下面讨论比较一下评价类方法，具体如下：

 

2-模糊综合评价的MATLAB编程实现

  我们可以看一下下面的例子4，对各方案的优劣进行评价。

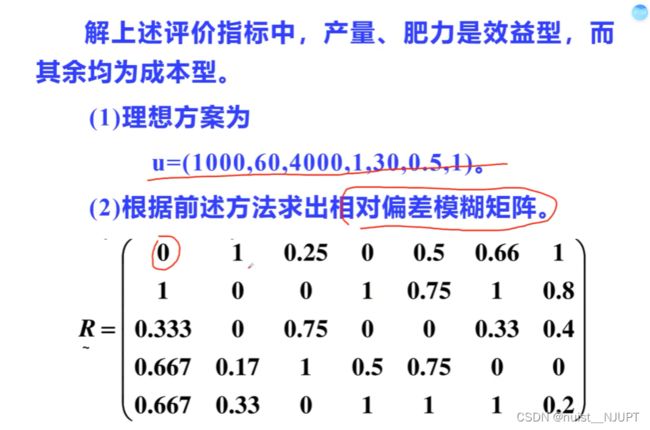
其中，产量和肥力属于效益型指标，其它的属于成本型指标。对于效益型理想型指标取最大值，对于成本型指标理想值取最小值。

下面思路对的，但是算错了，肥力应该越大越好，所有u的最后一个值是6，而不是1.

 根据理想方案和上述公式求出相对偏差模糊矩阵，具体如下所示：

 

 这个答案是错误的，因为理想方案中最后一个值是6，而不是1.

正确的各方案加权平均方差为： 0.5844   0.5950   0.4041   0.2887   0.4473

故各方案的优劣次序为4，3，5，1，2

对于上面的例子4，具体的编程实现如下所示，代码已加注释。

A = [1000, 120, 5000, 1, 50, 1.5, 1; 
      700, 60, 4000, 2, 40, 2, 2;
      900, 60, 7000, 1, 70, 1, 4;
      800, 70, 8000, 1.5, 40, 0.5, 6;
      800, 80, 4000, 2, 30, 2, 5] ;
  [m,n] = size(A) ; %找出矩阵A的行数和列数
  maxA = max(A) ; %找出每列的最大值，形成一个行向量
  minA = min(A) ; %找出每列的最小值，形成一个行向量
  G = maxA - minA ; %每列最大值减去最小值形成的行向量
  A1 = max(A(:,1)) ; %A1为效益型
  A2 = min(A(:,2:6)) ; %A2-A6为成本型
  A3 = max(A(:,7)) ; %A7为效益型
  u = [A1, A2, A3];  %得到理想型矩阵u
  %求出模糊综合矩阵R
  R = zeros(m, n) ;
  for i = 1 : m 
      for j = 1 : n 
          R(i,j) = abs(A(i,j) - u(j)) / G(j) ;
      end
  end
  
  %使用变异系数法求权重向量
  x = mean(A) ; %求均值
  s = std(A) ; %求标准差
  v = s./x ;
  v2 = sum(v) ;
  c = zeros(1,7) ; %得到各个指标的权重
  
  for i =  1 : 7
      c(i) = v(i) / v2 ;
  end
  
  FF = R * c' ;
  disp(FF) ;
  

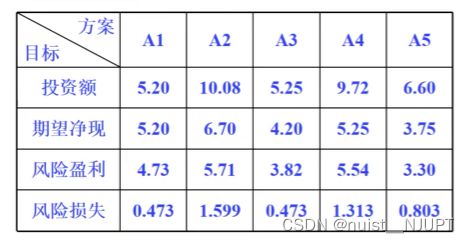
假如我们对如下5个方案进行优劣评价，具体如下：

 

 

对于上面的例子，具体的编程实现如下所示，代码已加注释。

A = [5.2, 5.2, 4.73, 0.473;
    10.08, 6.7, 5.71, 1.599; 
    5.25, 4.2, 3.82, 0.473;
    9.72, 5.25, 5.54, 1.313;
    6.6, 3.75, 3.3, 0.803] ;
[m,n] = size(A) ;
maxA = max(A) ;
minA = min(A) ;


%建立相对优属度模糊矩阵
R = zeros(m,n) ;

for i = 1 : m 
    for j = 1 : n 
        if (j==1 || j==4)
            R(i,j) = minA(j) / A(i,j) ;
        end
        if (j == 2 || j ==3)
            R(i,j) = A(i,j) / maxA(j) ;
        end
    end
end

x = mean(A) ;
s = std(A) ;
v = s ./ x ;
v2 = sum(v) ;
w = zeros(1,4) ;

for i = 1 : 4 
    w(i) = v(i) / v2 ;
end

  FF = R * w' ;
  disp(FF) ;

写的有点点混乱，总结一下吧：

模糊综合评价用于解决数学建模中的评价类问题，具体的步骤如下：

第1步：确定评级指标和评价等级。

第2步：构造模糊综合评价矩阵(主观打分法，客观的相对偏差法和相对优属度法)

第3步：确定评价指标的权重(不区分重要性:变量系数法，区分重要性：层次分析法)

第4步：模糊合成和综合评价