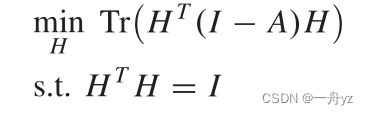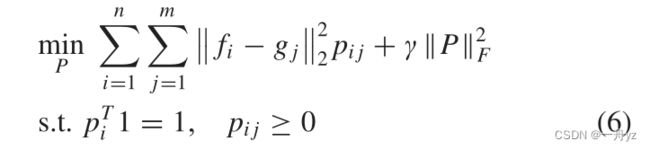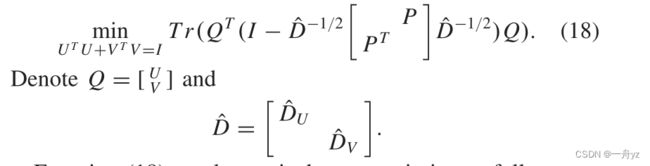基于结构图学习的大规模高光谱图像快速光谱嵌入聚类,FSECSGL
Fast Spectral Embedded Clustering Based on Structured Graph Learning for Large-Scale Hyperspectral Image
基于结构图学习的大规模高光谱图像快速光谱嵌入聚类
首先,通过快速光谱嵌入方法获得数据的低维表示,降低尺度;然后,我们利用嵌入的数据通过结构化图学习来学习最优的相似矩阵。此外,学习结构图对原始二部图进行反馈,生成更好的光谱嵌入数据。通过迭代可以得到更好的相似矩阵和聚类结果,克服了k均值初始化的局限性。
该方法的优点可以描述为三个部分:
- 提出了一种新的具有快速光谱嵌入和结构化图学习的联合聚类模型。该方法基于快速光谱嵌入的低维表示,在HSI图像中具有更好的性能和更小的计算复杂度。
- 该方法通过迭代可以同时学习到较好的相似矩阵和聚类结果,避免了K-means的初始化限制。
- 将学习相似度矩阵作为修改二部图的反馈,可以改进二部图的结构。
算法实现
快速光谱嵌入表示
采用快速光谱嵌入的方法来获得二部图结构。
使用kmeans方法生成m个聚类中心作为锚,比随机选择的锚更有代表性。
锚点: U = [ u 1 , … , u m ] T ∈ R m × d U = [u_1,\dots,u_m]^T \in R^{m \times d} U=[u1,…,um]T∈Rm×d
数据点: X = [ x 1 , … , x n ] T ∈ R n × d X = [x_1,\dots,x_n]^T \in R^{n \times d} X=[x1,…,xn]T∈Rn×d
通过解决以下问题获得二部图:
该方法使用无参数策略,无需设置 μ \mu μ。
令 d i j = ∥ x i − u j ∥ 2 2 d_{ij} = \lVert x_i - u_j \rVert _2^2 dij=∥xi−uj∥22 d i ∈ R m × 1 d_i \in R^{m \times 1} di∈Rm×1 Z 1 ∈ R n × m 的解可表示为: Z_1 \in R^{n \times m} 的解可表示为: Z1∈Rn×m的解可表示为:
锚点之间图结构的获取过程类似于数据点和锚点的图构造。由此,我们可以得到 Z 2 ∈ R m × m Z_2 ∈R^{m \times m} Z2∈Rm×m ,为锚点之间的二部矩阵。
此时,我们获得从原始数据中提取的特征映射 Z = [ Z 1 Z 2 ] Z=\begin{bmatrix} Z_1 \\ Z_2 \end{bmatrix} Z=[Z1Z2] ,相似矩阵可以通过对角矩阵 Λ ∈ R m × m \Lambda \in R^{m \times m} Λ∈Rm×m
A = Z Λ − 1 Z T (3) A = Z \Lambda ^{-1} Z^T \tag{3} A=ZΛ−1ZT(3)
H = [ F G ] H = \begin{bmatrix} F \\ G \end{bmatrix} H=[FG]是新的指标矩阵,目标函数可以定义为:
其中 F ∈ R n × c F ∈ R^{n×c} F∈Rn×c和 G ∈ R m × c G ∈ R^{m×c} G∈Rm×c是数据点和锚点的谱嵌入表示。因此,H的最优解是对A进行特征值分解
基于结构化学习的聚类
在本节中,我们的目标是通过在数据嵌入空间中迭代来获得聚类结果。因此,我们能够从嵌入的数据F和G中学习优化的相似性矩阵。因此,我们可以得到:
P是相似矩阵, p i p_i pi是行向量
fi是F的第i个样本,gj是G的第j个样本
应用先验知识来平衡样本和任务之间的关系以免获得平凡解:
矩阵P不能直接用于聚类,因为在大多数情况下,数据都与P相关联。
定理1:拉普拉斯矩阵L的特征值0的重数c等于具有相似矩阵s的图中连通分量的个数。
如果拉普拉斯矩阵的秩等于n+m-c,则聚类结果将具有精确的c聚类。因此,我们将秩约束添加到(6)中,即:
事实上,秩约束的求解是一个非常困难的问题。因此,我们将 σ k ( L P ) \sigma _k(LP) σk(LP)表示为LP的第k个最小特征值。秩约束可以转化为解决特征值问题:
其中 λ \lambda λ是一个足够大的参数,根据kyfans定理:
在这种情况下,可以控制概率邻居的分配过程,从而将数据准确地划分为c个簇。因此,在邻域分配中获得的矩阵P可以直接用于聚类
联系
为了生成更好的谱嵌入数据,我们观察到相似矩阵和二部图具有相同的结构,因此相似矩阵P可以作为更新原始二部图的反馈。更新后的规则可以描述为:
为了保持相同的形式,我们对更新后的矩阵进行规范化,得到新的二部图
当二部矩阵 Z = [ Z 1 ^ Z ] Z = \begin{bmatrix} \hat{Z_1} \\ Z \end{bmatrix} Z=[Z1^Z]更新时,可以将其代入(4)中,以生成更好的图嵌入数据
优化
我们使用两个过程来学习优化的相似矩阵。第一步是求解(4),这与对矩阵A进行特征值分解相同,来得到嵌入数据。在这种情况下,我们主要求解(9),而优化过程如下所示。
当Q固定,有表达式:
对于不同的i,问题是相互独立的,因此我们可以如下优化每个子问题:
当P固定时,Q的优化可以是:
等式(18)可以等价于优化如下:
其中U和V分别是对应于 红色划线部分 的最大c奇异值的左奇异向量和右奇异向量