哈工大机器学习实验二逻辑回归(牛顿法、梯度下降)
一、实验目的
- 理解逻辑回归模型
- 掌握逻辑回归模型的参数估计算法(带正则项和不带正则项)
二、实验要求及环境
实验要求:
- 实现两种损失函数的参数估计(1,无惩罚项;2.加入对参数的惩罚),可以采用梯度下降、共轭梯度或者牛顿法等。
- 验证:1.可以手工生成两个分别类别数据(可以用高斯分布),验证你的算法。考察类条件分布不满足朴素贝叶斯假设,会得到什么样的结果。 2. 逻辑回归有广泛的用处,例如广告预测。可以到UCI网站上,找一实际数据加以测试。
实验环境
- x86-64,Win 10
- Pycharm 2019.1
- python 3.7
三、设计思想
3.1算法原理
-
二项逻辑回归模型:
P ( Y = 0 ∣ x ) = 1 1 + e ω ⋅ x + b P(Y=0|x)=\frac{1}{1+e^{\omega · x+b}} P(Y=0∣x)=1+eω⋅x+b1
P ( Y = 1 ∣ x ) = e ω ⋅ x + b 1 + e ω ⋅ x + b P(Y=1|x)=\frac{e^{\omega · x +b}}{1+e^{\omega · x+b }} P(Y=1∣x)=1+eω⋅x+beω⋅x+b
其中 x ∈ R n x\in R^n x∈Rn是输入,Y ∈ \in ∈{0,1}是输出, ω ∈ R n \omega \in R^n ω∈Rn和 b ∈ R b\in R b∈R是参数, ω \omega ω称为权值向量,b称为偏置, ω ⋅ x \omega · x ω⋅x为 ω \omega ω和x的内积。有时为了方便,将权值向量和输入向量加以扩充,仍然记为 ω \omega ω和 x x x,但是 ω = ( ω 1 , ω 2 , . . . , ω n , b ) T \omega = (\omega^1,\omega^2,...,\omega^n,b)^T ω=(ω1,ω2,...,ωn,b)T, x = ( x 1 , x 2 , . . . , x n , 1 ) T x=(x^1,x^2,...,x^n,1)^T x=(x1,x2,...,xn,1)T。在这种情况下,二项逻辑回归模型如下:
P ( Y = 0 ∣ x ) = 1 1 + e ω ⋅ x P(Y=0|x)=\frac{1}{1+e^{\omega · x}} P(Y=0∣x)=1+eω⋅x1
P ( Y = 1 ∣ x ) = e ω ⋅ x 1 + e ω ⋅ x P(Y=1|x)=\frac{e^{\omega · x }}{1+e^{\omega · x }} P(Y=1∣x)=1+eω⋅xeω⋅x
定义sigmoid函数为 s i g m o i d ( z ) = 1 1 + e − z sigmoid(z)=\frac{1}{1+e^{-z}} sigmoid(z)=1+e−z1 -
似然函数法估计模型参数 ω \omega ω
设 P ( Y = 1 ∣ x ) = π ( x ) P(Y=1|x)=\pi(x) P(Y=1∣x)=π(x), P ( Y = 0 ∣ x ) = 1 − π ( x ) P(Y=0|x) = 1-\pi(x) P(Y=0∣x)=1−π(x),则似然函数为
∏ [ π ( x i ) ] y i [ 1 − π ( x i ) ] 1 − y i \prod [\pi(x_i)]^{y_i}[1-\pi(x_i)]^{1-y_i} ∏[π(xi)]yi[1−π(xi)]1−yi
对数似然函数为
L ( ω ) = ∑ i = 1 N [ y i l o g π ( x i ) + ( 1 − y i ) l o g ( 1 − π ( x i ) ) ] L(\omega) = \sum_{i=1}^{N}[y_ilog\pi(x_i)+(1-y_i)log(1-\pi(x_i))] L(ω)=i=1∑N[yilogπ(xi)+(1−yi)log(1−π(xi))]
= ∑ i = 1 N [ y i ( ω ⋅ x i ) − l o g ( 1 + e ω ⋅ x i ) ] =\sum_{i=1}^{N}[y_i(\omega · x_i)-log(1+e^{\omega·x_i})] =i=1∑N[yi(ω⋅xi)−log(1+eω⋅xi)]
不加正则项的损失函数为
L ( ω ) = ∑ i = 1 N [ − y i ( ω ⋅ x i ) + l o g ( 1 + e ω ⋅ x i ) ] L(\omega) = \sum_{i=1}^{N}[-y_i(\omega · x_i)+log(1+e^{\omega·x_i})] L(ω)=i=1∑N[−yi(ω⋅xi)+log(1+eω⋅xi)]
加入正则项的损失函数
L ( ω ) = − 1 N ∑ i = 1 N [ y i l o g π ( x i ) + ( 1 − y i ) l o g ( 1 − π ( x i ) ) ] + λ 2 N ∣ ∣ ω ∣ ∣ 2 2 L(\omega) =-\frac{1}{N} \sum_{i=1}^{N}[y_ilog\pi(x_i)+(1-y_i)log(1-\pi(x_i))] +\frac{\lambda}{2N}||\omega||_2^2 L(ω)=−N1i=1∑N[yilogπ(xi)+(1−yi)log(1−π(xi))]+2Nλ∣∣ω∣∣22
= 1 N ∑ i = 1 N [ − y i ( ω ⋅ x ) + l o g ( 1 + e ω ⋅ x i ) ] + λ 2 N ∣ ∣ ω ∣ ∣ 2 2 =\frac{1}{N}\sum_{i=1}^{N}[-y_i(\omega · x)+log(1+e^{\omega·x_i})]+\frac{\lambda}{2N}||\omega||_2^2 =N1i=1∑N[−yi(ω⋅x)+log(1+eω⋅xi)]+2Nλ∣∣ω∣∣22
求L ( ω ) 的 极 大 值 (\omega)的极大值 (ω)的极大值,得到 ω \omega ω的估计值
不加正则项求 ω \omega ω
∂ L ∂ w j = x i j ( − y i + s i g m o i d ( w x i ) ) \frac{\partial L}{\partial w_j}=x_{ij}(-y_i + sigmoid(wx_i)) ∂wj∂L=xij(−yi+sigmoid(wxi))
接下来可以由随机梯度下降法求解 ω \omega ω
同理加入正则项的梯度为
∂ L ∂ w j = 1 N [ x i j ( − y i + s i g m o i d ( w x i ) ) + λ ⋅ ω ] \frac{\partial L}{\partial w_j}=\frac{1}{N}[x_{ij}(-y_i + sigmoid(wx_i))+\lambda · \omega] ∂wj∂L=N1[xij(−yi+sigmoid(wxi))+λ⋅ω]
- 牛顿法
假设 L ( ω ) L(\omega ) L(ω)具有二阶连续偏导数,若第k次的迭代值为 ω ( k ) \omega ^{(k)} ω(k),则可将 L ( ω ) L(\omega ) L(ω)在 ω ( k ) \omega ^{(k)} ω(k)附近进行二阶泰勒展开:
L ( ω ) = L ( ω ( k ) ) + g k T ( ω − ω ( k ) ) + 1 2 ( ω − ω ( k ) ) T H ( ω ( k ) ) ( ω − ω ( k ) ) L(\omega)=L(\omega^{(k)})+g_k^{T}(\omega-\omega^{(k)})+\frac{1}{2}(\omega-\omega^{(k)})^TH(\omega^{(k)})(\omega-\omega^{(k)}) L(ω)=L(ω(k))+gkT(ω−ω(k))+21(ω−ω(k))TH(ω(k))(ω−ω(k))
这里, g k = g ( ω ( k ) ) = ▽ L ( ω ( k ) ) g_k=g(\omega^{(k)})=\triangledown L(\omega^{(k)}) gk=g(ω(k))=▽L(ω(k))是 L ( ω ) L(\omega) L(ω)的梯度向量在 ω ( k ) \omega^{(k)} ω(k)处的值, H ( ω ( k ) ) H(\omega^{(k)}) H(ω(k))是 L ( ω ) L(\omega) L(ω)的黑塞矩阵
H ( ω ) = [ ∂ 2 L ∂ ω i ∂ ω j ] n × n H(\omega)=[\frac{\partial ^{2}L}{\partial \omega_i\partial \omega_j}]_{n\times n} H(ω)=[∂ωi∂ωj∂2L]n×n
在 ω ( k ) \omega^{(k)} ω(k)处的值。函数 L ( ω ) L(\omega) L(ω)取得极值的必要条件是一阶导数为0(即梯度为0) ▽ L ( ω ) = 0 \triangledown L(\omega) = 0 ▽L(ω)=0
假设在迭代过程中第k+1次迭代使得 ▽ L ( ω ) = 0 \triangledown L(\omega)=0 ▽L(ω)=0,则有
▽ L ( ω ) = g k + H k ( ω − ω ( k ) ) \triangledown L(\omega) = g_k + H_k(\omega-\omega^{(k)}) ▽L(ω)=gk+Hk(ω−ω(k))将 H k = H ( ω ( k ) ) H_k=H(\omega^{(k)}) Hk=H(ω(k))代入,有
g k + H k ( ω ( k + 1 ) − ω ( k ) ) = 0 g_k+H_k(\omega^{(k+1)-\omega^{(k)}})=0 gk+Hk(ω(k+1)−ω(k))=0
因此可得迭代式 ω ( k + 1 ) = ω ( k ) − H k − 1 g k \omega^{(k+1)}=\omega^{(k)}-H_k^{-1}g_k ω(k+1)=ω(k)−Hk−1gk
3.2算法的实现
3.2.0.变量:
- matrix = () # 读入数据矩阵
- test_matrix = () # 测试数据矩阵
- y = () # 分类情况,y[i]表示第i组数据的分类情况
- test_y = () # 测试数据集的分类情况
- x = () # 特征矩阵,其中x[i]表示第i个实例的特征取值情况,最后一维为1
- test_x = () # 测试数据集的特征矩阵
- w = () # 对应扩充特征后的w
- n = 0 # 特征数的个数,其中w是n+1维的
- dataSum = 0 # 数据量
- testSum = 0 # 测试数据集大小
3.2.1.生成数据(2维)
满足贝叶斯:协方差矩阵半正定,例如 c o v = ( 1 0 0 1 ) cov=(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}) cov=(1001)
不满足贝叶斯:当协方差不等于0时,两个参数相关,则不独立,例如,2维数据均相关,不独立 c o v = ( 2 1 1 2 ) cov=(\begin{array}{cc} 2 & 1 \\ 1 & 2 \end{array}) cov=(2112)
可以调用numpy.random.multivariate_normal生成多维高斯分布数据
3.2.2.读取数据
使用pandas.read_csv读取csv格式的数据,然后再将读入的DataFrame结构使用.valus转化为ndarray,然后使用矩阵切片和扩充生成x,y
3.2.3.随机梯度下降法
自行设置迭代次数door,每次选取一组数据,根据以下公式进行求解,观察不同迭代次数的收敛情况
∂ L ∂ w j = x i j ( − y i + s i g m o i d ( w x i ) ) \frac{\partial L}{\partial w_j}=x_{ij}(-y_i + sigmoid(wx_i)) ∂wj∂L=xij(−yi+sigmoid(wxi))
3.2.4 牛顿法
每迭代一次计算一次黑塞矩阵设置迭代次数,按次数迭代可得 ω \omega ω。
3.2.5. 计算正确率
计算 ω ⋅ x \omega·x ω⋅x的值,与0比较,若大于或者等于零预测为1;小于0预测为0.统计预测正确的样本数,计算预测的正确率。
四、实验结果与分析
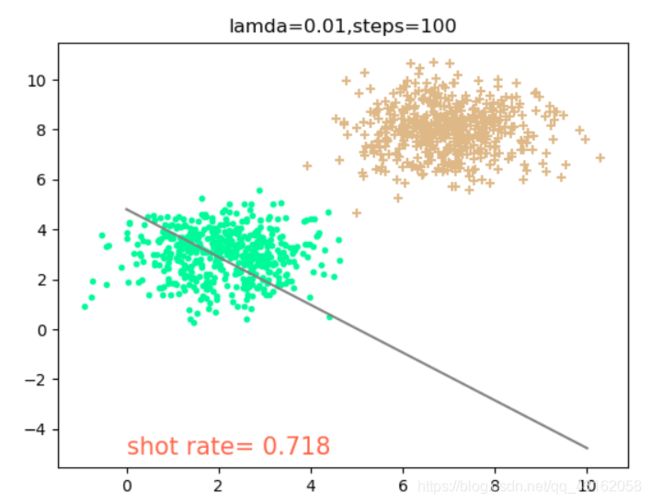
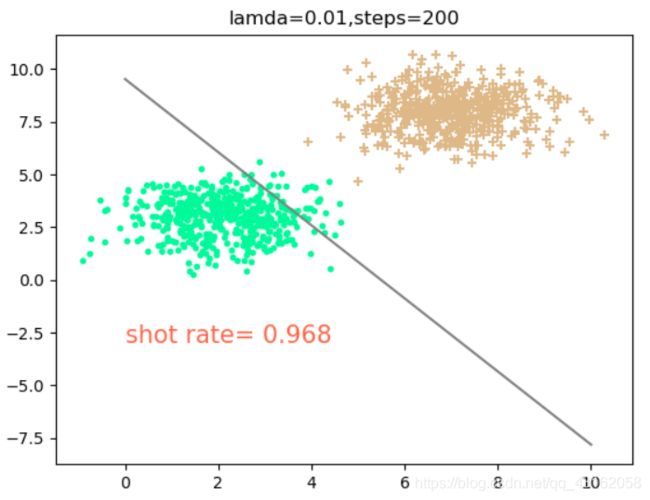
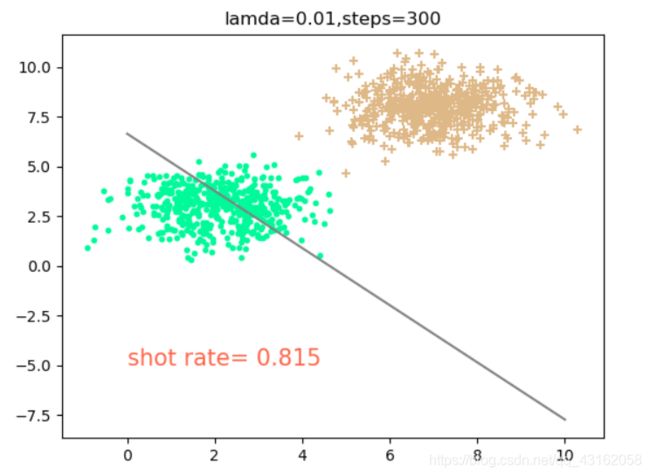
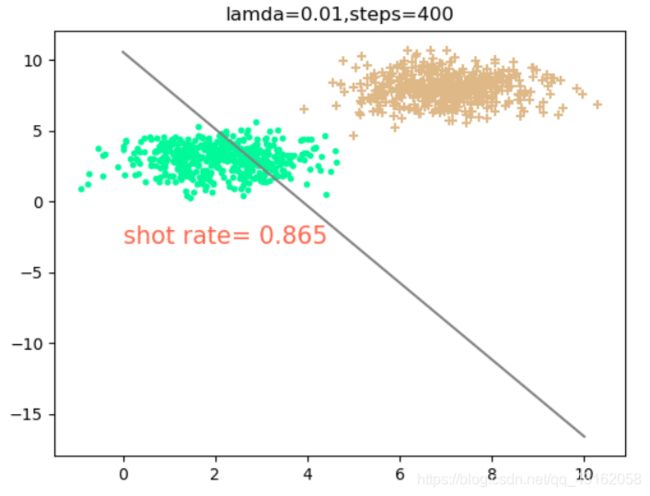
4.1 讨论不同的学习率下,需要的随机梯度下降次数

可以得出,当lamda=0.01时,学习率比较大(这里不讨论过拟合),因此所需迭代的步数比较小,大约在100-200次能够拟合得比较好,当大于200次以后出现震荡现象,反而使得正确率下降。但是随机梯度下降法由于每次选择样本是随机的,所以不一定每次分类效果都很好。
4.2 相同步数和学习率,讨论不同正则因子对分类效果的影响
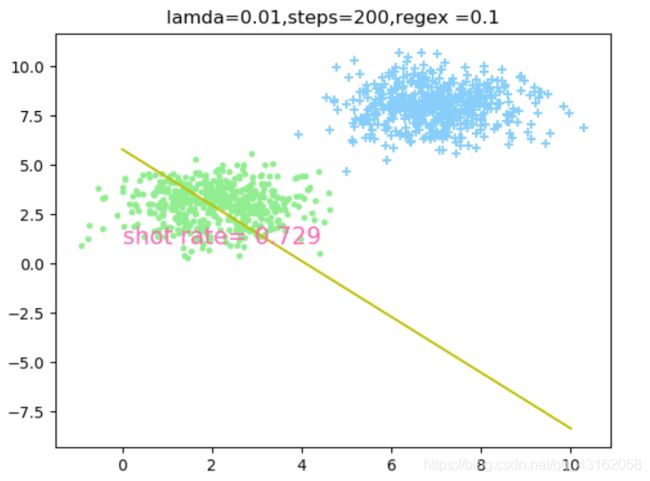
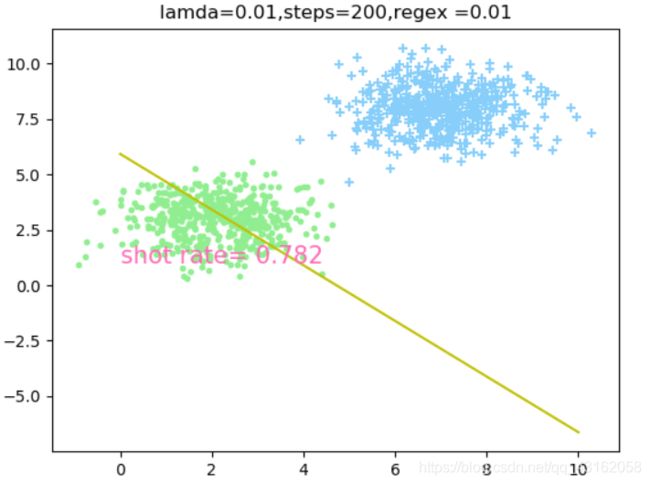

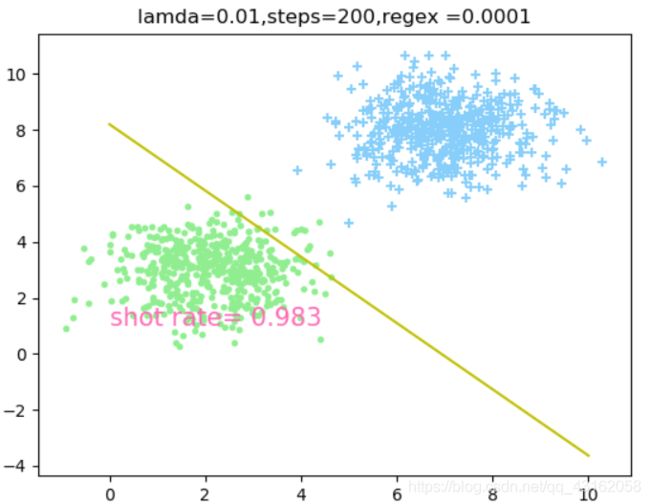
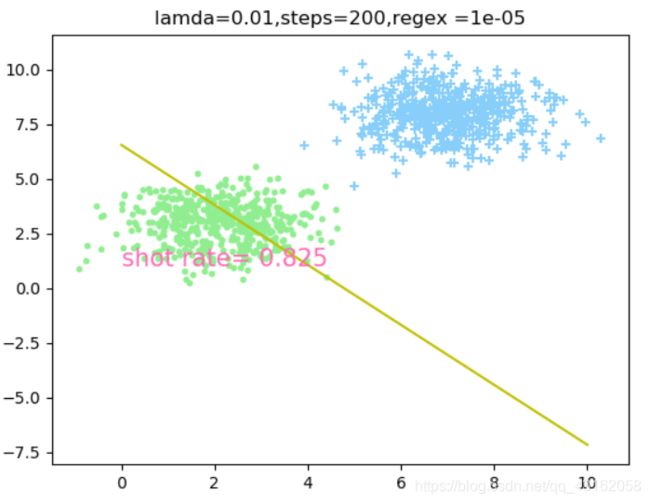
由此可以得出当lamda = 0.01,steps = 200时,正则因子regex = 0.0001时分类效果最好。
4.3生成数据验证
不加正则项
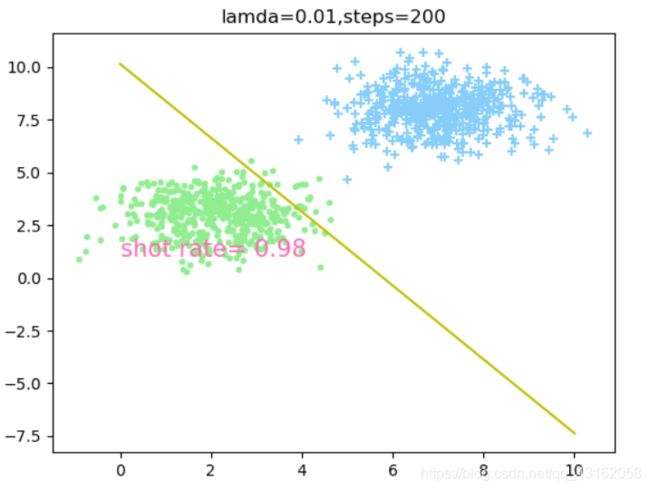
加入正则项

使用随机梯度下降法优化,由于样本选择是随机的,因此每次的正确率不一定相同,但大多数时候正确率都超过0.85,有时候甚至能到达0.95以上。
4.4 数据满足贝叶斯假设和不满足贝叶斯假设进行对比
4.4.1不加正则项
4.4.2 加入正则项
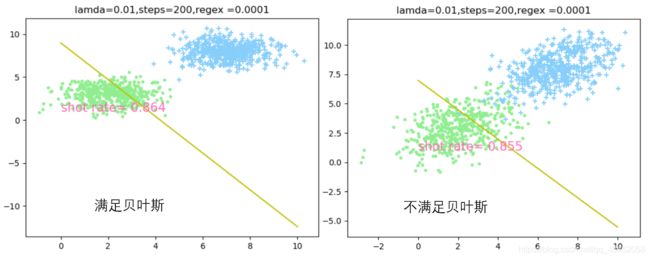
由图片可知,无论加不加正则项,满足贝叶斯假设与否对逻辑回归的正确率的影响不大,但是满足贝叶斯假设的数据分类效果略胜一筹。
4.5 使用UCI数据集测试
在UCI上寻找了一个判断是否会税务欺诈的数据集,筛选特征后只剩四维数据,使用正则和非正则观察分类效果
4.6 牛顿法优化
牛顿法相比梯度下降法,需要的迭代次数更少,而且更容易得到最优解,因此正确率很容易超过0.98,有时候甚至可以达到1.0
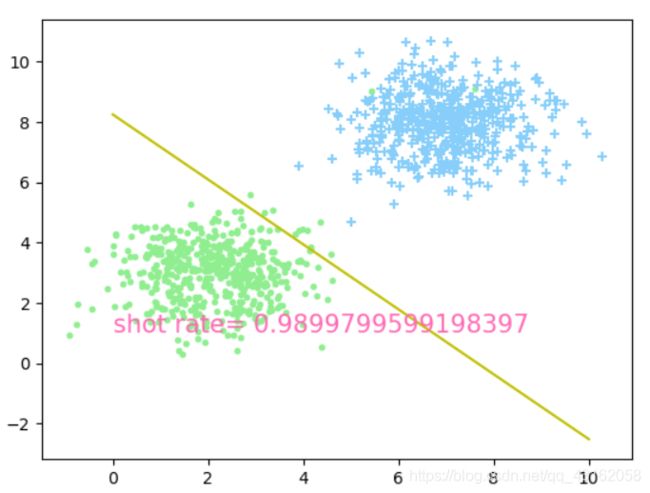
4.7 在实验过程中发现的问题
- 实验中sigmoid函数很容易溢出,可以对自变量进行讨论,如果自变量z的值小于20,则认为sigmoid为0.
- 计算加入正则因子的 ω \omega ω时,如果数据量过大(约1000以上),而且采用float32来进行计算,会因为精度丢失而无法成功分类。解决方法有两种,一是将loss乘以数据量,这样可以避免精度丢失,但是会有上溢出的风险;而是所有相关数据均使用float64类型,但是float64占用内存较大,运行速度相对缓慢。本实验中我使用的数据可以直接采用乘数据量解决,因此使用的这个办法解决了精度丢失的问题。
五、结论
- 关于惩罚项: 对于逻辑回归而言,带正则项和不带正则项的差别没有多项式拟合函数那么大。尤其是当使用随机梯度下降法时,由于随机梯度下降法选择样本的不确定性,在相同迭代次数和相同参数条件下,基本无法看出显著差异。但是使用牛顿法进行优化时,由于比较容易找到最小值,所以如果不加正则项会发生过拟合。
- 关于牛顿法:牛顿法每次迭代的时间代价为O( N ⋅ ∣ w ∣ 2 N·|w|^2 N⋅∣w∣2),相比梯度下降法,每次的时间开销和空间占用会更大。但是牛顿法仅需大约10-15次就能找到最小值,比梯度下降法快得多(200次左右)。但是牛顿法的计算过程中涉及求黑塞矩阵的逆,如果矩阵奇异,则牛顿法不再适用。
- 关于精度:python编译器默认浮点数为float32,有时候精度丢失会比较严重,如果需要使用float64表示数据,需要自己手动设置
- 关于sigmoid函数,sigmoid函数可能会发生溢出,主要是当z<<0时时 e z e^z ez>>0,会发生溢出。
六、参考文献
【统计学习方法】李航
【机器学习】周志华
七、源代码(含注释)
import numpy as np
import math
import matplotlib.pyplot as plt
import pandas as pd
import random
"""
by xiaoyi
"""
class Logistic:
matrix = () # 读入数据矩阵
test_matrix = () # 测试数据矩阵
y = () # 分类情况,y[i]表示第i组数据的分类情况
test_y = () # 测试数据集的分类情况
x = () # 特征矩阵,其中x[i]表示第i个实例的特征取值情况,最后一维为1
test_x = () # 测试数据集的特征矩阵
w = () # 对应扩充特征后的w
n = 0 # 特征数的个数,其中w是n+1维的
dataSum = 0 # 数据量
testSum = 0 # 测试数据集大小
# sigmoid函数
@staticmethod
def sig(wx):
if wx < -10:
return 0
else:
return 1 / (1 + math.exp(-wx))
# 计算对数似然的值,不加正则,梯度上升法,没有加负号
def cal_loss1(self):
loss = 0
for i in range(self.dataSum):
w_multi_x = np.dot(self.x[i], self.w)
# print(w_multi_x)
loss -= np.dot(self.y[i], w_multi_x)
# 防止溢出,所以对wx进行讨论
if w_multi_x > 0:
loss += w_multi_x + math.log(1 + math.exp(-w_multi_x))
else:
loss += math.log(1 + math.exp(w_multi_x))
return loss
# 计算损失函数的值,加正则,梯度下降法,加负号
def cal_loss2(self, regex):
loss = 0
for i in range(self.dataSum):
# print(self.x[i])
w_multi_x = np.dot(np.mat(self.x[i]), self.w)
# print(w_multi_x)
loss -= np.dot(self.y[i], w_multi_x)
# 防止溢出,所以对wx进行讨论
if w_multi_x > 0:
loss += w_multi_x + math.log(1 + math.exp(-w_multi_x))
else:
loss += math.log(1 + math.exp(w_multi_x))
loss += regex * np.dot(self.w.T, self.w)[0, 0]
# loss /= self.dataSum
return loss
下降法
def cal_gradient1(self):
gradient = np.zeros((self.n + 1, 1))
i = random.randint(0, self.dataSum - 1)
wx = np.dot(np.mat(self.x[i]), self.w)
for j in range(self.n + 1):
gradient[j][0] += self.x[i][j] * (-self.y[i] + Logistic.sig(wx))
return gradient
# 计算梯度,带正则,损失函数的梯度
def cal_gradient2(self, regex):
gradient = np.zeros((self.n + 1, 1))
i = random.randint(0, self.dataSum - 1)
wx = np.dot(np.mat(self.x[i]), self.w)
for j in range(self.n + 1):
gradient[j][0] += self.x[i][j] * (-self.y[i] + Logistic.sig(wx))
gradient += regex * self.w
# print(gradient)
# gradient /= self.dataSum
# print(gradient)
return gradient
# 使用梯度下降法优化参数,似然函数,不带正则
def de_gradient1(self, lamda, door):
# print(self.w)
loss0 = self.cal_loss1()
g0 = self.cal_gradient1()
w0 = self.w
self.w -= lamda * g0
loss1 = self.cal_loss1()
cnt = 0
while cnt < door:
cnt += 1
loss0 = loss1
g0 = self.cal_gradient1()
w0 = self.w
self.w -= lamda * g0
loss1 = self.cal_loss1()
# print(loss0 - loss1)
self.w = w0
# print(self.w)
# 返回损失函数的值
return loss0
# 使用梯度下降法求解带正则项的w
def de_gradient2(self, lamda, door, regex):
loss0 = self.cal_loss2(regex)
g0 = self.cal_gradient2(regex)
w0 = self.w
self.w -= lamda * g0
loss1 = self.cal_loss2(regex)
cnt = 0
while cnt < door:
# print(loss1 - loss0)
# print(g0)
cnt += 1
loss0 = loss1
g0 = self.cal_gradient2(regex)
w0 = self.w
self.w -= lamda * g0
loss1 = self.cal_loss2(regex)
self.w = w0
# 返回损失函数的值
return loss0
# 计算黑塞矩阵
def hessian(self):
he = np.zeros((self.n + 1, self.n + 1))
for i in range(self.dataSum):
w_multi_x = np.dot(np.mat(self.x[i]), self.w)
# print(w_multi_x)
for j in range(self.n + 1):
for k in range(self.n + 1):
if w_multi_x > 20:
he[j][k] -= 0
else:
p = Logistic.sig(w_multi_x)
he[j][k] += self.x[i][j] * self.x[i][k] * p * (1 - p)
return he
# 牛顿法
def newton(self, steps):
cnt = 0
w0 = self.w
while cnt < steps:
cnt += 1
g = self.cal_gradient1()
# print(g)
he = self.hessian()
# print(np.linalg.inv(he))
w0 = self.w
# print(self.w)
self.w -= np.dot(np.linalg.inv(he), g)
self.w = w0
# 读取训练集
def read_data(self, file):
self.matrix = pd.read_csv(file, header=1).values
# print(self.matrix)
# with open(file) as f:
# self.matrix = np.loadtxt(f, float, delimiter=",")
self.dataSum = len(self.matrix)
self.n = len(self.matrix[0]) - 1
add = np.ones((self.dataSum, 1))
self.x = np.hstack((self.matrix[:, :self.n], add))
# print(self.x)
self.y = self.matrix[:, self.n]
self.w = np.ones((self.n + 1, 1))
# 读取测试集
def read_test_data(self, file):
self.test_matrix = pd.read_csv(file, header=1).values
# with open(file) as f:
# self.test_matrix = np.loadtxt(f, float, delimiter=',')
self.testSum = len(self.test_matrix)
self.test_x = np.hstack((self.test_matrix[:, :self.n], np.ones((self.testSum, 1))))
self.test_y = self.test_matrix[:, self.n]
# 预测
def pre_test(self):
cnt = 0
for i in range(self.testSum):
pre_wx = np.dot(np.mat(self.test_x[i]), self.w)
# print(pre_wx)
if (pre_wx >= 0) and (self.test_y[i] == 1):
cnt += 1
elif (pre_wx <= 0) and (self.test_y[i] == 0):
cnt += 1
return cnt / self.testSum
def test_model():
# 测试模型
test = Logistic()
train_set = "gauss.csv"
test_set = "test_gauss.csv"
test.read_data(train_set)
lamda = 1e-2
steps = 10
regex = 1e-3
# test.de_gradient2(lamda, steps, regex)
# test.de_gradient1(lamda, steps)
test.newton(steps)
test.read_test_data(test_set)
correct = test.pre_test()
print(correct)
x0 = test.test_matrix[:500, 0]
y0 = test.test_matrix[:500, 1]
x1 = test.test_matrix[500:, 0]
y1 = test.test_matrix[500:, 1]
plt.scatter(x0, y0, marker='.', color='lightgreen')
plt.scatter(x1, y1, marker='+', color='lightskyblue')
dx = np.linspace(0, 10, 100)
dy = (-test.w[2][0] - test.w[0][0] * dx) / test.w[1][0]
# plt.title("lamda=" + str(lamda) + ",steps=" + str(steps)+",regex ="+str(regex))
# plt.title("lamda=" + str(lamda) + ",steps=" + str(steps))
plt.plot(dx, dy, color='y')
ans = "shot rate= " + str(correct)
plt.text(0, 1, ans, color='hotpink', fontsize=15)
plt.show()
def generate_data():
# 生成高斯数据
f = open('test_gauss_not_bayes.csv', 'w')
mean0 = [2, 3]
cov = np.mat([[2, 1], [1, 2]])
x0 = np.random.multivariate_normal(mean0, cov, 500).T
mean1 = [7, 8]
x1 = np.random.multivariate_normal(mean1, cov, 500).T
for i in range(len(x0.T)):
line = []
line.append(x0[0][i])
line.append(x0[1][i])
line.append(1)
line = ",".join(str(i) for i in line)
line = line + "\n"
f.write(line)
for i in range(len(x0.T)):
line = []
line.append(x1[0][i])
line.append(x1[1][i])
line.append(0)
line = ",".join(str(i) for i in line)
line += "\n"
f.write(line)
f.close()
test_model()