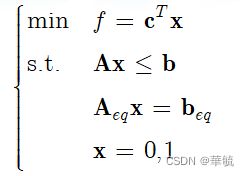0-1规划的MATLAB求解
0-1规划问题的MATLAB标准型
1、在上述模型中,目标函数f 需要 “极小化”,不等式约束形式为 “≤”。假设x为n维设计变量,且线性规划问题具有不等式约束m1个,等式约束m2个,那么:c、x均为n维列向量,b为m1维列向量,beq为m2维列向量,A为m1×n维矩阵,Aeq为m2×n维矩阵。
2、如果不满足标准型的要求,则需要对原问题进行转化,化为标准型之后才能使用相关函数,标准化的方法和线性规划中的类似
0-1规划问题的MATLAB求解函数
MATLAB优化工具箱中求解0-1规划问题的命令为bintprog
x = bintprog(f)
x = bintprog(f,A,b)
x = bintprog(f,A,b,Aeq,beq)
x = bintprog(f,A,b,Aeq,beq,x0)
x = bintprog(f,A,b,Aeq,Beq,x0,options)
[x,fval] = bintprog(...)
[x,fval,exitflag] = bintprog(...)
[x,fval,exitflag,output] = bintprog(...)
输入参数
MATLAB工具箱中的bintprog函数在求0-1规划问题时,提供的参数有如下几种:
模型参数: x、c、b、beq、A和Aeq
初始解参数:x0
算法控制参数: options,我们可以通过optimset命令对这些具体的控制参数进行设置,其中主要参数的设置方法如下所示:

输出参数
1、x为0-1规划问题的最优解
2、fval为0-1规划问题在最优解x处的函数值
3、exitflag返回的是bintprog计算终止时的状态指示,说明算法终止的原因,其取值和其代表的具体原因如表所示。
4、输出参数output是一个返回优化过程中相关信息的结构变量,它所包含的属性及属性代表的意义如表所示。
参数exitflag的物理意义
参数output所包含的信息
0-1规划问题的命令详解
x = bintprog(f) %该函数调用格式求解如下形式的0-1规划问题
x = bintprog(c,A,b) %该函数调用格式求解如下形式的0-1规划问题
x = bintprog (c,A,b,Aeq,beq) %该函数调用格式求解如下形式的0-1规划问题
x = bintprog (c,A,b,Aeq,beq,x0) % 在前一个调用格式的基础上同时设置求解算法的初始解为x0,
如果初始解x0不在0-1规划问题的可行域中,算法将采用默认的初始解
x = bintprog (c,A,b,Aeq,beq,x0,options) % 用options指定的优化参数进行最小化.
可以使用optimset来设置这些参数
[x,fval] = bintprog(...) % 在优化计算结束之时返回整数规划问题在解x处的目标函数值fval
[x,fval,exitflag] = bintprog(...) % 在优化计算结束之时返回exitflag值,
描述函数计算的退出条件。
[x,fval,exitflag,output] = bintprog(...)`% 在优化计算结束之时返回结构变量output
实例

c=[20;6;8;9];
A=[-10 -6 -5 -2; -7 -2 -2 -4; -2 -1 -1 -10; 0 1 1 -1];b=[-4;-4;-2;1];
lb=[0;0;0;0];ub=[1;1;1;1];
M=1:4; %均要求为整数变量
Tol=1e-8; %判断是否整数的误差限
[x,fval]=intprog(c,A,b,[],[],lb,ub,M,Tol) %调用intprog函数
[x1,fval1]=bintprog(c,A,b) %调用bintprog函数