三角函数（Python，机器学习）

直角三角形的边长与夹角

直角三角形是指一个三角形中有一个角是90度。

边长：有a、b、c等3个边长

边长的名词：a是高、b是底、c是斜边。

直角：a（高）与b（底）的夹角是直角。

：b与c的夹角，念作Theta。

三角形的3个角加总是180度，减掉直角，可以得到a与c的夹角是-。

 

三角函数的定义

        a=高        c=斜边

        b=底        c=斜边

        a=高        b=底

计算三角形的面积

省略

角度与弧度

弧度又称径度，一般是用rad代表。

角度360度对应的弧度是2

常见的角度、弧度转换表

角度值	弧度值	角度值	弧度值
30		120
45		135
60		150
90		180

列出角度值为30、45、60、120、135、150、180的角的弧度值。

import math

degrees = [30, 45, 60, 90, 120, 135, 150, 180]
for degree in degrees:
    print('角度 = {0:3d},   弧度 = {1:6.3f}'.format(degree, math.pi*degree/180))

运行结果如下：

[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
角度 =  30,   弧度 =  0.524
角度 =  45,   弧度 =  0.785
角度 =  60,   弧度 =  1.047
角度 =  90,   弧度 =  1.571
角度 = 120,   弧度 =  2.094
角度 = 135,   弧度 =  2.356
角度 = 150,   弧度 =  2.618
角度 = 180,   弧度 =  3.142

[Done] exited with code=0 in 0.296 seconds

弧长是指圆周上曲线的长度。

计算圆形弧长的通用公式，假设角度是：

计算半径是10厘米，角度值 是30、60、90、120的对应弧长值。

import math

degrees = [30, 60, 90, 120]
r = 10
for degree in degrees:
    curve = 2 * math.pi * r * degree / 360
    print('角度 = {0:3d},   弧长 = {1:6.3f}'.format(degree, curve))

运行结果如下：

[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
角度 =  30,   弧长 =  5.236
角度 =  60,   弧长 = 10.472
角度 =  90,   弧长 = 15.708
角度 = 120,   弧长 = 20.944

[Done] exited with code=0 in 0.301 seconds

假设圆半径是r，扇形角度是，扇形面积计算公式：

计算半径是10厘米，角度值是30、60、90、120的对应扇形面积值。

import math

degrees = [30, 60, 90, 120]
r = 10
for degree in degrees:
    area = math.pi * r * r * degree / 360
    print('角度 = {0:3d},   扇形面积 = {1:6.3f}'.format(degree, area))

运行结果：

[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
角度 =  30,   扇形面积 = 26.180
角度 =  60,   扇形面积 = 52.360
角度 =  90,   扇形面积 = 78.540
角度 = 120,   扇形面积 = 104.720

[Done] exited with code=0 in 0.425 seconds

 

程序处理三角函数

每隔，列出角度的孤度与sin()和cos()的值。 

import math

degrees = [x*30 for x in range(0,13)]
for d in degrees:
    rad = math.radians(d)
    sin = math.sin(rad)
    cos = math.cos(rad)
    print('角度={0:3d}, 弧度={1:5.2f}, sin{2:3d}={3:5.2f}, cos{4:3d}={5:5.2f}'
          .format(d, rad, d, sin, d, cos))

运行结果如下：

[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
角度=  0, 弧度= 0.00, sin  0= 0.00, cos  0= 1.00
角度= 30, 弧度= 0.52, sin 30= 0.50, cos 30= 0.87
角度= 60, 弧度= 1.05, sin 60= 0.87, cos 60= 0.50
角度= 90, 弧度= 1.57, sin 90= 1.00, cos 90= 0.00
角度=120, 弧度= 2.09, sin120= 0.87, cos120=-0.50
角度=150, 弧度= 2.62, sin150= 0.50, cos150=-0.87
角度=180, 弧度= 3.14, sin180= 0.00, cos180=-1.00
角度=210, 弧度= 3.67, sin210=-0.50, cos210=-0.87
角度=240, 弧度= 4.19, sin240=-0.87, cos240=-0.50
角度=270, 弧度= 4.71, sin270=-1.00, cos270=-0.00
角度=300, 弧度= 5.24, sin300=-0.87, cos300= 0.50
角度=330, 弧度= 5.76, sin330=-0.50, cos330= 0.87
角度=360, 弧度= 6.28, sin360=-0.00, cos360= 1.00

[Done] exited with code=0 in 1.662 seconds

从单位圆看三角函数

假设有一个圆，半径是1，圆周上有一个点P，P点的坐标是。

在圆角上每隔标注点。

import matplotlib.pyplot as plt
import math

degrees = [x*15 for x in range(0,25)]
x = [math.cos(math.radians(d)) for d in degrees]
y = [math.sin(math.radians(d)) for d in degrees]

plt.scatter(x,y)
plt.axis('equal')
plt.grid()
plt.show()

运行结果如下：

 

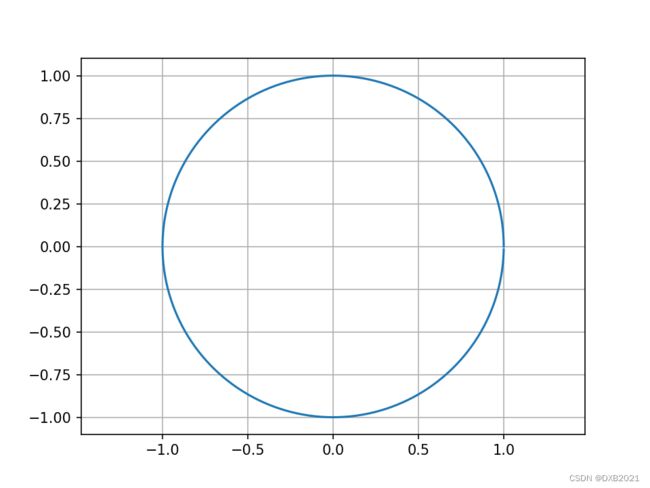
使用三角函数绘制半径是1的圆。

import matplotlib.pyplot as plt
import numpy as np

degrees = np.arange(0, 360)
x = np.cos(np.radians(degrees))
y = np.sin(np.radians(degrees))

plt.plot(x,y)
plt.axis('equal')
plt.grid()
plt.show()

运行结果如下：