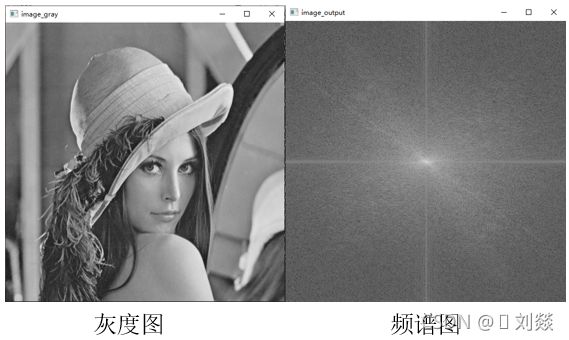
c++ opencv数字图像处理：频率域滤波基础，傅里叶变换及频谱图

---

前言

数字图像处理c++ opencv（VS2019 opencv4.53）持续更新

---

一、傅里叶级数及傅里叶变换

傅立叶变换如何理解？美颜和变声都是什么原理？李永乐老师告诉你

【官方双语】形象展示傅里叶变换

---

二、二维图像中的傅里叶变换

1.基本原理公式（离散傅里叶变换（DFT）,离散傅里叶逆变换（IDFT））

（1）一维离散傅里叶变换：

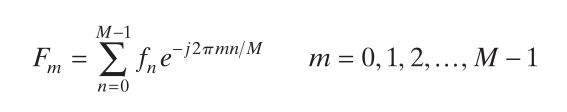
一维离散傅里叶逆变换：

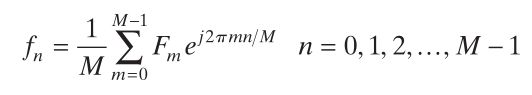
（2）二维离散傅里叶变换：

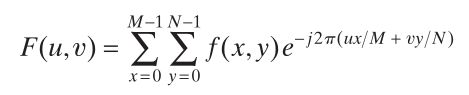
二维离散傅里叶逆变换：

---

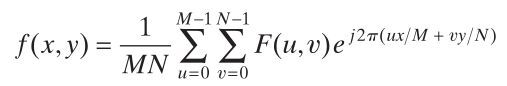
2.opencv傅里叶变换c++代码

参考：
1
2

#include
#include
#include

using namespace cv;
using namespace std;


//定义傅里叶变换函数。input_image：输入图像；output_image：傅里叶频谱图；transform_array:傅里叶变换矩阵（复数）
void My_DFT(Mat input_image, Mat& output_image, Mat& transform_array);

int main()
{ 
	Mat image, image_gray, image_output, image_transform;   //定义输入图像，灰度图像，输出图像
	image = imread("lena.png");  //读取图像；
	if (image.empty())
	{
		cout << "读取错误" << endl;
		return -1;
	}
	imshow("image", image);

	cvtColor(image, image_gray, COLOR_BGR2GRAY); //转换为灰度图
	imshow("image_gray", image_gray); //显示灰度图

	//傅里叶变换，image_output为可显示的频谱图，image_transform为傅里叶变换的复数结果
	My_DFT(image_gray, image_output, image_transform);
	imshow("image_output", image_output);

	waitKey(0);  //暂停，保持图像显示，等待按键结束
	return 0;
}


//傅里叶变换得到频谱图和复数域结果
void My_DFT(Mat input_image, Mat& output_image, Mat& transform_image)
{
	//1.扩展图像矩阵，为2，3，5的倍数时运算速度快
	int m = getOptimalDFTSize(input_image.rows);
	int n = getOptimalDFTSize(input_image.cols);
	copyMakeBorder(input_image, input_image, 0, m - input_image.rows, 0, n - input_image.cols, BORDER_CONSTANT, Scalar::all(0));

	//2.创建一个双通道矩阵planes，用来储存复数的实部与虚部
	Mat planes[] = { Mat_<float>(input_image), Mat::zeros(input_image.size(), CV_32F) };

	//3.从多个单通道数组中创建一个多通道数组:transform_image。函数Merge将几个数组合并为一个多通道阵列，即输出数组的每个元素将是输入数组元素的级联
	merge(planes, 2, transform_image);

	//4.进行傅立叶变换
	dft(transform_image, transform_image);

	//5.计算复数的幅值，保存在output_image（频谱图）
	split(transform_image, planes); // 将双通道分为两个单通道，一个表示实部，一个表示虚部
	magnitude(planes[0], planes[1], output_image); //计算复数的幅值，保存在output_image（频谱图）

	//6.前面得到的频谱图数级过大，不好显示，因此转换
	output_image += Scalar(1);   // 取对数前将所有的像素都加1，防止log0
	log(output_image, output_image);   // 取对数
	normalize(output_image, output_image, 0, 1, NORM_MINMAX); //归一化

	//7.剪切和重分布幅度图像限
	output_image = output_image(Rect(0, 0, output_image.cols & -2, output_image.rows & -2));

	  // 重新排列傅里叶图像中的象限，使原点位于图像中心
	int cx = output_image.cols / 2;
	int cy = output_image.rows / 2;
	Mat q0(output_image, Rect(0, 0, cx, cy));   // 左上区域
	Mat q1(output_image, Rect(cx, 0, cx, cy));  // 右上区域
	Mat q2(output_image, Rect(0, cy, cx, cy));  // 左下区域
	Mat q3(output_image, Rect(cx, cy, cx, cy)); // 右下区域

	  //交换象限中心化
	Mat tmp;
	q0.copyTo(tmp); q3.copyTo(q0); tmp.copyTo(q3);//左上与右下进行交换
	q1.copyTo(tmp); q2.copyTo(q1); tmp.copyTo(q2);//右上与左下进行交换
}

结果：

---

3.频谱图

（1）频谱图从中心点到四周，频率越来越大；
（2）频谱图中心点一般最亮，与原图像平均亮度相关；
（3）频率域滤波就是改变频谱图中高频率或者低频率的值.
（4）频谱图中的点关于中心点对称，对称的两点表示某个频率的波。
（5）两个对称点离中心点的距离代表频率的高低，离中心点越远代表的频率越高。
（6）两个对称点的亮度表示波的幅值，越亮幅值越大。
（7）图像中，低频率代表灰度变化缓慢的信息；高频率代表变化剧烈的信息，如边缘及噪声等。在（6）中，低频区越亮代表变化缓慢的区域较多，高频区越亮代表图像细节很多。
（8）对称点所在直线的方向为波的方向，与原图中对应的线性信息垂直。如下图，图中有一组平行的线，在频谱图垂直方向也有一条较亮的线（可用于方向滤波，增强或者滤除某个方向的线性特征）。