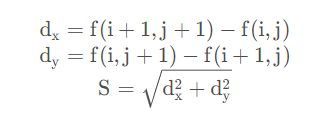OpenCV数字图像处理基于C++：边缘检测

OpenCV数字图像处理基于C++：边缘检测

1、概述

边缘检测是图像处理和计算机视觉中的基本问题，边缘检测的目的是标识数字图像中亮度变化明显的点。图像属性中的显著变化通常反映了属性的重要事件和变化。
图像边缘检测大幅度地减少了数据量，并且剔除了可以认为不相关的信息，保留了图像重要的结构属性。有许多方法用于边缘检测，它们的绝大部分可以划分为两类:基于查找和基于零穿越。
基于查找:通过寻找图像一阶导数中的最大值和最小值来检测边界，然后利用计算结果估计边缘的局部方向，通常采用梯度的方向，并利用此方向找到局部梯度模的最大值，代表算法是 Sobel 算子、Roberts 算子、 Scharr 算子和差分边缘检测。
基于零穿越︰通过寻找图像二阶导数零穿越来寻找边界，代表算法是拉普拉斯（Laplacian）算子或者非线性差分表示的过零点。

边缘一般是指图像在某一局部强度剧烈变化的区域。强度变化一般有两种情况：
阶跃变化：

像数值从低到高变化，图像从暗到亮

山顶变化：

• 找到有差异的相邻像素（边缘检测）
• 增加有差异的像素的对比度（图像锐化）

边缘检测步骤：

（1）图像获取

（2）图像滤波

边缘检测的算法主要是基于图像强度的一阶和二阶导数，但是导数通常对噪声很敏感，因此必须采用滤波器来改善与噪声有关的边缘检测器的性能。

（3）图像增强

增强边缘检测的基础是确定图像各点的领域强度的变化值。增强算法可以将图像灰度点领域强度值 有显著变化的点凸显出来。

（4）图像检测

（5）图像定位

2、差分边缘检测

2.1 原理

使用图像的一阶差分代替图像函数的导数。二维离散图像函数在x方向上的一阶差分定义为，y方向上为，其中前者计算垂直边边缘，后者计算水平边缘。

2.2 实现差分边缘检测

// 图像差分操作
void diffOperation(const cv::Mat srcImage, cv::Mat& edgeXImage, cv::Mat& edgeYImage)
{
	cv::Mat tempImage = srcImage.clone();
	int nRows = tempImage.rows;
	int nCols = tempImage.cols;
	for (int i = 0; i < nRows - 1; i++)
	{
		for (int j = 0; j < nCols - 1; j++)
		{
			// 计算垂直边边缘
			edgeXImage.at(i, j) =
				abs(tempImage.at(i + 1, j) -
					tempImage.at(i, j));
			// 计算水平边缘
			edgeYImage.at(i, j) =
				abs(tempImage.at(i, j + 1) -
					tempImage.at(i, j));
		}
	}
}

int main()
{
	cv::Mat srcImage = cv::imread("E:\\Lena.jpg");
	if (!srcImage.data)
		return -1;
	cv::imshow("srcImage", srcImage);
	cv::Mat edgeXImage(srcImage.size(), srcImage.type());
	cv::Mat edgeYImage(srcImage.size(), srcImage.type());
	// 计算差分图像
	diffOperation(srcImage, edgeXImage, edgeYImage);
	cv::imshow("edgeXImage1", edgeXImage);
	cv::imshow("edgeYImage2", edgeYImage);
	cv::Mat edgeImage(srcImage.size(), srcImage.type());
	// 水平与垂直边缘图像叠加
	addWeighted(edgeXImage, 0.5, edgeYImage,
		0.5, 0.0, edgeImage);
	cv::imshow("edgeImage3", edgeImage);
	cv::waitKey(0);
	return 0;
}

3、Roberts算子边缘检测

3.1 原理

Roberts算子与普通梯度算子类似，都是取一阶的差分作为梯度，区别在于取值的位置：

正对角为水平方向，斜对角为垂直方向：

Roberts算法优缺点
优点：Roberts算子能较好的增强正负45度的图像边缘
缺点：对边缘的定位不太准确，提取的边缘线条较粗

3.2 实现Roberts算子边缘检测

//Roberts算子实现
Mat roberts(Mat srcImage)
{
	Mat dstImage = srcImage.clone();
	int nRows = dstImage.rows;
	int nCols = dstImage.cols;
	for (int i = 0; i < nRows - 1; i++) {
		for (int j = 0; j < nCols - 1; j++) {
			//根据公式计算
			int t1 = (srcImage.at(i, j) -
				srcImage.at(i + 1, j + 1)) *
				(srcImage.at(i, j) -
					srcImage.at(i + 1, j + 1));
			int t2 = (srcImage.at(i + 1, j) -
				srcImage.at(i, j + 1)) *
				(srcImage.at(i + 1, j) -
					srcImage.at(i, j + 1));
			//计算g（x,y）
			dstImage.at(i, j) = (uchar)sqrt(t1 + t2);
		}
	}
	return dstImage;
}

int main()
{
	Mat srcImage = imread("E:\\la.jpg");
	if (!srcImage.data) {
		cout << "falied to read" << endl;
		system("pause");
		return -1;
	}
	Mat srcGray;
	cvtColor(srcImage, srcGray, CV_BGR2GRAY);
	//高斯滤波
	GaussianBlur(srcGray, srcGray, Size(3, 3),
		0, 0, BORDER_DEFAULT);
	Mat dstImage = roberts(srcGray);
	imshow("srcImage", srcImage);
	imshow("dstImage", dstImage);
	waitKey(0);
	return 0;
}

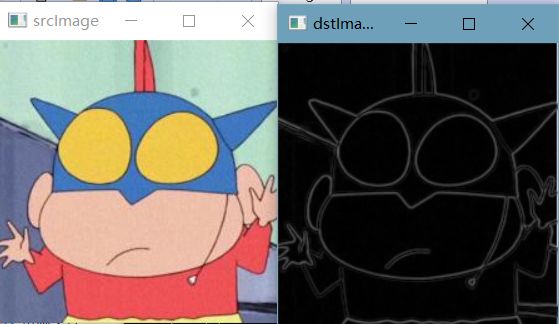
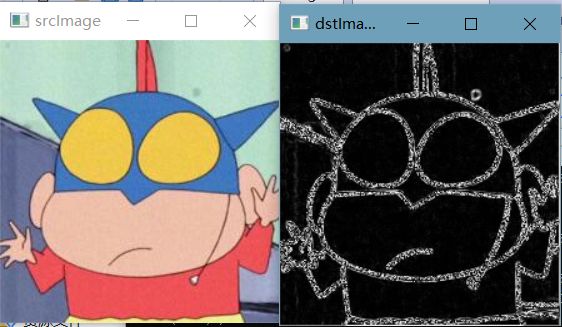
（1）g（x,y） = sqrt(t1 + t2)

（2）g（x,y） = max(t1,t2)

4、Prewitt算子边缘检测

4.1 原理

​ Prewitt算子是一种一阶微分算子的边缘检测，利用像素点上下、左右邻点的灰度差，在边缘处达到极值检测边缘，去掉部分伪边缘，对噪声具有平滑作用 。其原理是在图像空间利用两个方向模板与图像进行邻域卷积来完成的，这两个方向模板一个检测水平边缘，一个检测垂直边缘。
​ prewitt算子是加权平均算子，对噪声有抑制作用，但是像素平均相当于对图像进行的同滤波，所以prewitt算子对边缘的定位不如robert算子。

标准的 Prewitt 边缘检测算子由以下两个卷积核组成。

4.2 手工实现 Prewitt 算子边缘检测

//Prewitt轮廓提取算法
Mat myPrewitt(Mat src,int x,int y) {
	//获取图像属性
	int nRows = src.rows;
	int nCols = src.cols;
	int dx = 0, dy = 0;
	//定义空白图像，用于存放Prewitt算法提取出来的轮廓图
	Mat dst(src.size(), src.type());
	//对阈值化图像进行遍历，进行Sober算法
	for (int i = 1; i < nRows - 1; i++) {
		for (int j = 1; j < nCols - 1; j++) {
			dx = min(255,abs((src.at(i + 1, j - 1) + src.at(i + 1, j ) + src.at(i + 1, j + 1))-(src.at(i - 1, j - 1) + src.at(i - 1, j) + src.at(i - 1, j + 1))));
			dy = min(255,abs((src.at(i - 1, j + 1) + src.at(i , j + 1 ) + src.at(i + 1, j + 1))-(src.at(i - 1, j - 1) + src.at(i , j - 1) + src.at(i + 1, j - 1)))) ;
			if (x == 0) {
				dst.at(i, j) = dy;
			}
			else {
				dst.at(i, j) = dx;
			}
			
		}
	}

	return dst;
}


int main()
{
	//读取图像，黑白图像边缘检测结果较为明显
	Mat img = imread("E:\\la.jpg", IMREAD_ANYCOLOR);
	if (img.empty())
	{
		cout << "请确认图像文件名称是否正确" << endl;
		return -1;
	}
	//显示图像
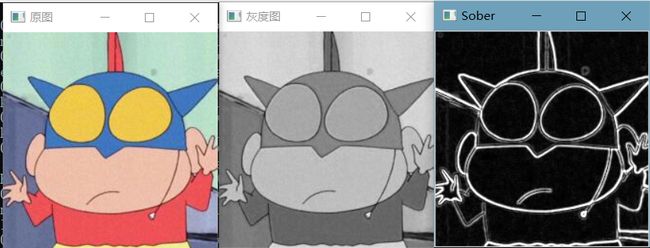
	imshow("原图", img);
	cvtColor(img, img, COLOR_RGB2GRAY);
	imshow("灰度图", img);
	GaussianBlur(img, img, Size(3, 3), 0); //高斯滤波器（模糊/平滑/近似）消除噪点
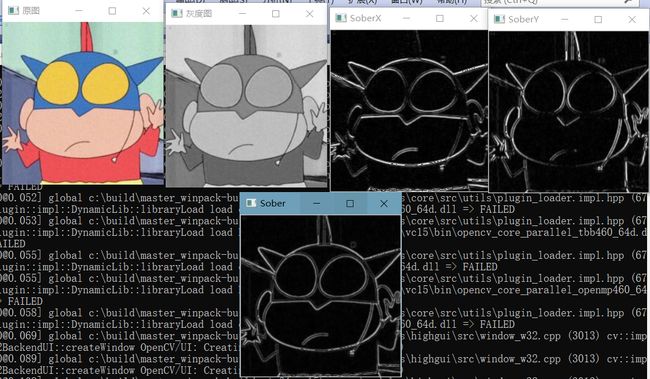
	Mat dstX = myPrewitt(img,1,0);
	imshow("SoberX", dstX);
	Mat dstY = myPrewitt(img, 0, 1);
	imshow("SoberY", dstY);
	convertScaleAbs(dstX, dstX);
	//imshow("SoberX2", dstX);
	convertScaleAbs(dstY, dstY);
	Mat dst;
	addWeighted(dstX, 0.5, dstY, 0.5, 0, dst);
	imshow("Sober", dst);
	waitKey(0);
	return 0;
}

（1）未用abs来防止是否越界

（2）用abs来防止是否越界

（3）g(x,y) = dx + dy

dst.at(i, j) = min(255,dx+dy);

convertScaleAbs()用于实现对整个图像数组中的每一个元素，进行如下操作：

4.3 函数实现 Prewitt 算子边缘检测

void getPrewitt_oper(Mat& getPrewitt_horizontal, Mat& getPrewitt_vertical, Mat& getPrewitt_Diagonal1, Mat& getPrewitt_Diagonal2) {
	//水平方向
	getPrewitt_horizontal = (Mat_(3, 3) << -1, -1, -1, 0, 0, 0, 1, 1, 1);
	//垂直方向
	getPrewitt_vertical = (Mat_(3, 3) << -1, 0, 1, -1, 0, 1, -1, 0, 1);
	//对角135°
	getPrewitt_Diagonal1 = (Mat_(3, 3) << 0, 1, 1, -1, 0, 1, -1, -1, 0);
	//对角45°
	getPrewitt_Diagonal2 = (Mat_(3, 3) << -1, -1, 0, -1, 0, 1, 0, 1, 1);

	//逆时针反转180°得到卷积核
	flip(getPrewitt_horizontal, getPrewitt_horizontal, -1);
	flip(getPrewitt_vertical, getPrewitt_vertical, -1);
	flip(getPrewitt_Diagonal1, getPrewitt_Diagonal1, -1);
	flip(getPrewitt_Diagonal2, getPrewitt_Diagonal2, -1);
}

void edge_Prewitt(Mat& src, Mat& dst1, Mat& dst2, Mat& dst3, Mat& dst4, Mat& dst, int ddepth, double delta = 0, int borderType = BORDER_DEFAULT) {
	//获取Prewitt算子
	Mat getPrewitt_horizontal;
	Mat getPrewitt_vertical;
	Mat getPrewitt_Diagonal1;
	Mat getPrewitt_Diagonal2;
	getPrewitt_oper(getPrewitt_horizontal, getPrewitt_vertical, getPrewitt_Diagonal1, getPrewitt_Diagonal2);

	//卷积得到水平方向边缘
	filter2D(src, dst1, ddepth, getPrewitt_horizontal, Point(-1, -1), delta, borderType);

	//卷积得到4垂直方向边缘
	filter2D(src, dst2, ddepth, getPrewitt_vertical, Point(-1, -1), delta, borderType);

	//卷积得到45°方向边缘
	filter2D(src, dst3, ddepth, getPrewitt_Diagonal1, Point(-1, -1), delta, borderType);

	//卷积得到135°方向边缘
	filter2D(src, dst4, ddepth, getPrewitt_Diagonal2, Point(-1, -1), delta, borderType);

	//边缘强度（近似）
	convertScaleAbs(dst1, dst1); //求绝对值并转为无符号8位图
	convertScaleAbs(dst2, dst2);

	convertScaleAbs(dst3, dst3); //求绝对值并转为无符号8位图
	convertScaleAbs(dst4, dst4);
	dst = dst1 + dst2;

}

int main()
{
	Mat dst, dst1, dst2, dst3, dst4;
	Mat img = imread("E:\\la.jpg");
	cvtColor(img, img, COLOR_BGR2GRAY);
	//注意：要采用CV_32F，因为有些地方卷积后为负数，若用8位无符号，则会导致这些地方为0
	edge_Prewitt(img, dst1, dst2, dst3, dst4, dst, CV_32F);
	imshow("原图", img);
	namedWindow("水平边缘", WINDOW_NORMAL);
	imshow("水平边缘", dst1);
	namedWindow("垂直边缘", WINDOW_NORMAL);
	imshow("垂直边缘", dst2);
	namedWindow("45°边缘", WINDOW_NORMAL);
	imshow("45°边缘", dst3);
	namedWindow("135°边缘", WINDOW_NORMAL);
	imshow("135°边缘", dst4);
	namedWindow("边缘强度", WINDOW_NORMAL);
	imshow("边缘强度", dst);
	waitKey(0);
	return 0;
}

5、Sobel算子边缘检测

5.1 原理

Sobel算法(索贝尔算子)是一种用于边缘检测的离散微分算子，它结合了高斯平滑和微分求导。该算子用于计算图像明暗程度近似值，根据图像边缘旁边明暗程度把该区域内超过某个数的特定点记为边缘。Sobel算子在Prewitt算子的基础上增加了权重的概念，认为相邻点的距离远近对当前像素点的影响是不同的，距离越近的像素点对应当前像素的影响越大，从而实现图像锐化并突出边缘轮廓。当对精度要求不是很高时，Sobel算子是一种较为常用的边缘检测方法。

Sobel算法提取图像边缘的三大步骤：

（1）提取X方向的边缘，即Gx；

以卷积核的中心为中心，将卷积核与图像上像素值一一对应，卷积核上的数字相当于系数。利用如下公式即可计算出卷积核中心的x方向梯度。

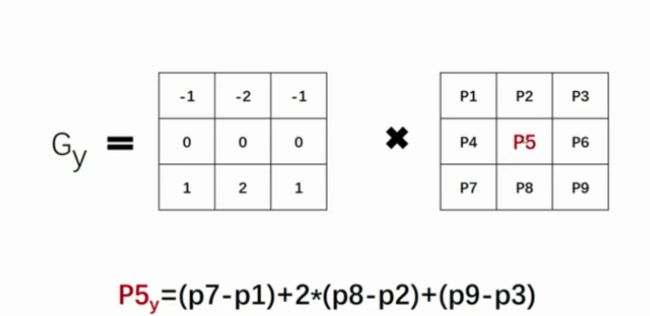
（2）提取Y方向的边缘，即Gy；

同理，如果想要计算y方向的梯度，卷积核应该是这样的，公式也是同理。

（3）综合两个方向的边缘信息得到整幅图的边缘。

Sobel算法优缺点
优点：Sobel算子的边缘定位更准确，会具有更多的抗噪性,不但产生较好的检测效果，而且对噪声具有平滑抑制作用；方法简单、处理速度快,并且所得的边缘光滑、连续
缺点：得到的边缘较粗，且可能出现伪边缘

5.2 手工实现 Sobel 算子边缘检测

//Sobel轮廓提取算法
Mat mySobel(Mat src) {
	//获取图像属性
	int nRows = src.rows;
	int nCols = src.cols;
	int dx = 0, dy = 0;
	//定义空白图像，用于存放Roberts算法提取出来的轮廓图
	Mat dst(src.size(), src.type());
	//对阈值化图像进行遍历，进行Sober算法
	for (int i = 1; i < nRows - 1; i++) {
		for (int j = 1; j < nCols - 1; j++) {
			dx = (src.at(i - 1, j + 1) - src.at(i - 1, j - 1)) + 2 * (src.at(i, j + 1) - src.at(i, j - 1)) + (src.at(i + 1, j + 1) - src.at(i + 1, j - 1));
			dy = (src.at(i + 1, j - 1) - src.at(i - 1, j - 1)) + 2 * (src.at(i + 1, j) - src.at(i -1 , j)) + (src.at(i + 1, j + 1) - src.at(i - 1, j + 1));
			dst.at(i, j) = sqrt(dx * dx + dy * dy);
		}
	}

	return dst;
}


int main()
{
	//读取图像，黑白图像边缘检测结果较为明显
	Mat img = imread("E:\\la.jpg", IMREAD_ANYCOLOR);
	if (img.empty())
	{
		cout << "请确认图像文件名称是否正确" << endl;
		return -1;
	}
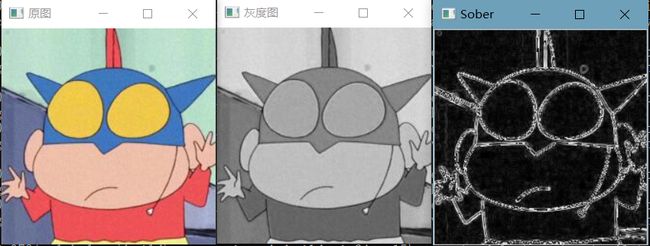
	//显示图像
	imshow("原图", img);
	cvtColor(img, img, COLOR_RGB2GRAY);
	imshow("灰度图", img);
	Mat dst = mySobel(img);
	imshow("Sober", dst);
	
	waitKey(0);
	return 0;
}

（1）未用abs来防止是否越界

（2）用abs来防止是否越界（开根号）

//对阈值化图像进行遍历，进行Sober算法
	for (int i = 1; i < nRows - 1; i++) {
		for (int j = 1; j < nCols - 1; j++) {
			dx = min(255,(src.at(i - 1, j + 1) - src.at(i - 1, j - 1)) + 2 * (src.at(i, j + 1) - src.at(i, j - 1)) + (src.at(i + 1, j + 1) - src.at(i + 1, j - 1)));
			dy = min(255,(src.at(i + 1, j - 1) - src.at(i - 1, j - 1)) + 2 * (src.at(i + 1, j) - src.at(i - 1, j)) + (src.at(i + 1, j + 1) - src.at(i - 1, j + 1)));
			dst.at(i, j) = min(255,(int)sqrt(dx * dx + dy * dy));
		}
	}

（3）直接使用dx和dy两者间的较大值

dst.at(i, j) = max(dx , dy);

法二：

Mat img = imread("E:\\la.jpg");
	cvtColor(img, img, COLOR_BGR2GRAY);
	Mat imageX = Mat::zeros(img.size(), CV_16SC1);
	Mat imageY = Mat::zeros(img.size(), CV_16SC1);
	Mat imageXY = Mat::zeros(img.size(), CV_16SC1);
	Mat imageX8UC;
	Mat imageY8UC;
	Mat imageXY8UC;

	GaussianBlur(img, img, Size(3, 3), 0); //高斯滤波器（模糊/平滑/近似）消除噪点
	uchar* P = img.data;
	uchar* PX = imageX.data;
	uchar* PY = imageY.data;
	int step = img.step;
	int stepXY = imageX.step;
	for (int i = 1; i < img.rows - 1; i++)
	{
		for (int j = 1; j < img.cols - 1; j++)
		{
			// 通过指针遍历图像上每一个像素
			// 求出X,Y方向的导数（梯度） sobel算子加权的结果
			PX[i * imageX.step + j * (stepXY / step)] = abs(P[(i - 1) * step + j + 1] + P[i * step + j + 1] * 2 + P[(i + 1) * step + j + 1] - P[(i - 1) * step + j - 1] - P[i * step + j - 1] * 2 - P[(i + 1) * step + j - 1]);
			PY[i * imageX.step + j * (stepXY / step)] = abs(P[(i + 1) * step + j - 1] + P[(i + 1) * step + j] * 2 + P[(i + 1) * step + j + 1] - P[(i - 1) * step + j - 1] - P[(i - 1) * step + j] * 2 - P[(i - 1) * step + j + 1]);
		}
	}
	addWeighted(imageX, 0.5, imageY, 0.5, 0, imageXY);//融合X、Y方向的梯度	
	convertScaleAbs(imageX, imageX8UC);
	convertScaleAbs(imageY, imageY8UC);
	convertScaleAbs(imageXY, imageXY8UC);   //转换为8bit图像

	Mat imageSobel;
	Mat x_grad, y_grad;
	Sobel(img, x_grad, CV_16S, 1, 0, 3);
	Sobel(img, y_grad, CV_16S, 0, 1, 3);
	convertScaleAbs(x_grad, x_grad);
	convertScaleAbs(y_grad, y_grad);
	addWeighted(x_grad, 0.5, y_grad, 0.5, 0, imageSobel);

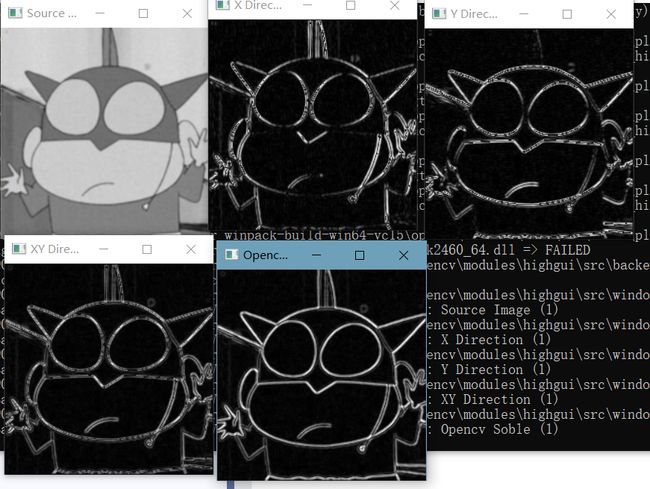
	imshow("Source Image", img);
	imshow("X Direction", imageX8UC);
	imshow("Y Direction", imageY8UC);
	imshow("XY Direction", imageXY8UC);
	imshow("Opencv Soble", imageSobel);
	waitKey(0);

addWeighted（）函数是将两张相同大小，相同类型的图片融合的函数。他可以实现图片的特效，不多说了，直接上图。
void addWeighted( const CvArr* src1, double alpha,const CvArr* src2, double beta,double gamma, CvArr* dst );
参数1：src1，第一个原数组.
参数2：alpha，第一个数组元素权重
参数3：src2第二个原数组
参数4：beta，第二个数组元素权重
参数5：gamma，图1与图2作和后添加的数值。不要太大，不然图片一片白。总和等于255以上就是纯白色了。
参数6：dst，输出图片
convertScaleAbs()用于实现对整个图像数组中的每一个元素，进行如下操作：
convertScaleAbs(
    cv::InputArray src, // 输入数组
    cv::OutputArray dst, // 输出数组
    double alpha = 1.0, // 乘数因子
    double beta = 0.0 // 偏移量
 );

5.3 函数实现 Sobel 算子边缘检测

int main()
{
	//读取图像，黑白图像边缘检测结果较为明显
	Mat img = imread("E:\\la.jpg", IMREAD_ANYCOLOR);
	if (img.empty())
	{
		cout << "请确认图像文件名称是否正确" << endl;
		return -1;
	}
	Mat resultX, resultY, resultXY;
	Sobel(img, resultX, CV_16S, 2, 0, 1);//X方向一阶边缘
	convertScaleAbs(resultX, resultX);
	Sobel(img, resultY, CV_16S, 0, 1, 3);//Y方向一阶边缘
	convertScaleAbs(resultY, resultY);
	resultXY = resultX + resultY;//整幅图像的一阶边缘
	//显示图像
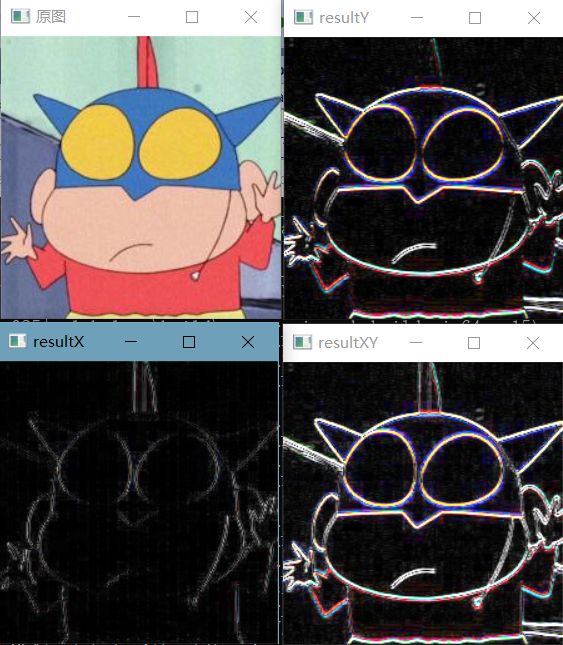
	imshow("原图", img);
	imshow("resultX", resultX);
	imshow("resultY", resultY);
	imshow("resultXY", resultXY);
	waitKey(0);
	return 0;
}

CV_EXPORTS_W void Sobel( 
    InputArray src, 
    OutputArray dst, 
    int ddepth,
    int dx, 
    int dy, 
    int ksize = 3,
    double scale = 1, 
    double delta = 0,
    int borderType = BORDER_DEFAULT 
);
参数说明：
src ：输入图像；
dst : 输出与src大小、通道数相同的图像;、
ddepth ：输出图像的深度，必须大于输入的图像数据类型,参见@ref filter_depth " combined ";在输入图像为8位的情况下会导致导数被截断。
dx : x的导数的阶次;
dy : y的导数的阶次;
ksize : 扩展Sobel内核的大小;它一定是1 3 5或7。
scale : 计算出的导数值选择尺度因子;默认情况下是1，不缩放；
delta : 表示在结果存入目标图（第二个参数dst）之前可选的delta值，有默认值0。
borderType : 边界的处理模式，默认值：BORDER_DEFAULT。

6、Laplace算子边缘检测(拉普拉斯)

6.1 原理

Laplacian算子具有各方向同性的特点，能够对任意方向的边缘进行提取，具有无方向性的优点，因此使用Laplacian算子提取边缘不需要分别检测X方向的边缘和Y方向的边缘，只需要一次边缘检测即可。利用拉普拉斯算子作边缘检测前最好先对图像作一个高斯滤波，效果会好不少。

Laplace 是导数算子，会突出图像中的急剧灰度变化，抑制灰度缓慢变化区域，往往会产生暗色背景下的灰色边缘和不连续图像。将拉普拉斯图像与原图叠加，可以得到保留锐化效果的图像。

6.2 手工实现 Laplace 算子边缘检测

//锐化算法
Mat& imgSharpen(const Mat& img, char* arith)       //arith为3*3模板算子
{
	int rows = img.rows;        //原图的行
	int cols = img.cols * img.channels();   //原图的列
	int offsetx = img.channels();       //像素点的偏移量

	static Mat dst = Mat::ones(img.rows - 2, img.cols - 2, img.type());

	for (int i = 1; i < rows - 1; i++)
	{
		const uchar* previous = img.ptr(i - 1);
		const uchar* current = img.ptr(i);
		const uchar* next = img.ptr(i + 1);
		uchar* output = dst.ptr(i - 1);
		for (int j = offsetx; j < cols - offsetx; j++)
		{
			output[j - offsetx] =
				saturate_cast(previous[j - offsetx] * arith[0] + previous[j] * arith[1] + previous[j + offsetx] * arith[2] +
					current[j - offsetx] * arith[3] + current[j] * arith[4] + current[j + offsetx] * arith[5] +
					next[j - offsetx] * arith[6] + next[j] * arith[7] + next[j - offsetx] * arith[8]);
		}
	}
	return dst;
}


//Laplace轮廓提取算法
Mat myLaplace(Mat src) {
	//获取图像属性
	int nRows = src.rows;
	int nCols = src.cols;
	int dx = 0, dy = 0;
	//定义空白图像，用于存放Roberts算法提取出来的轮廓图
	Mat dst(src.size(), src.type());
	//对阈值化图像进行遍历，进行Sober算法
	for (int i = 1; i < nRows - 1; i++) {
		for (int j = 1; j < nCols - 1; j++) {
			//防止越界
			dst.at(i, j) = saturate_cast(src.at(i - 1,j) + src.at(i + 1, j) + src.at(i, j - 1) + src.at(i , j - 1) - 4 * src.at(i, j));
		}
	}

	return dst;
}


int main()
{
	char arith[9] = { 0, -1, 0, -1, 5, -1, 0, -1, 0 };       //使用拉普拉斯算子
	//读取图像，黑白图像边缘检测结果较为明显
	Mat img = imread("E:\\la.jpg", IMREAD_ANYCOLOR);
	if (img.empty())
	{
		cout << "请确认图像文件名称是否正确" << endl;
		return -1;
	}
	//显示图像
	imshow("原图", img);
	/*img = imgSharpen(img, arith);
	imshow("Sharpen", img);*/
	cvtColor(img, img, COLOR_RGB2GRAY);
	imshow("灰度图", img);
	//高斯滤波器（模糊/平滑/近似）消除噪点
	GaussianBlur(img, img, Size(3, 3), 0);
	
	img = imgSharpen(img,arith);
	imshow("Sharpen2", img);
	convertScaleAbs(img, img);
	Mat dst = myLaplace(img);
	imshow("Laplace", dst);

	waitKey(0);
	return 0;
}

（1）未使用高斯滤波进行降噪

（2）使用高斯滤波进行降噪，但未锐化

（3）使用高斯滤波进行降噪，且锐化

6.3 函数实现 Laplace 算子边缘检测

int main() {
    Mat img = imread("E:\\la.jpg", IMREAD_GRAYSCALE);
    if (img.empty()) {
        cerr << "image file read error" << endl;
        return -1;
    }
   // resize(im, im, Size(0, 0), 0.5, 0.5);

    Mat result1, resultGauss, result2;
    // 未使用高斯滤波进行边缘检测
    Laplacian(img, result1, -1, 3);
    convertScaleAbs(result1, result1);

    // 先用高斯滤波器进行滤波后再进行边缘检测
    GaussianBlur(img, resultGauss, Size(3, 3), 0);
    Laplacian(resultGauss, result2, -1, 3);
    convertScaleAbs(result2, result2);
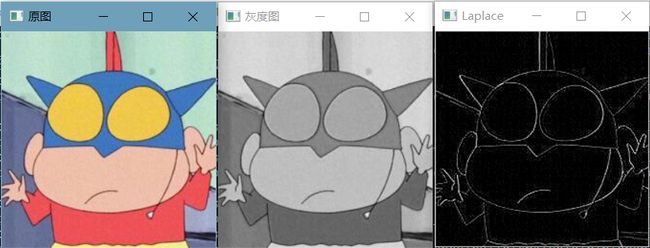
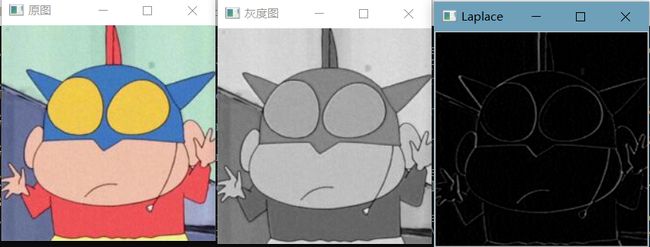
    imshow("原图", img);
    imshow("result1", result1);
    imshow("result2", result2);

    waitKey(0);
    destroyAllWindows();

    return 0;
}

去掉GaussianBlur(img, resultGauss, Size(3, 3), 0);这句代码的效果

void cv::Laplacian(    InputArray  src,
                       OutputArray  dst,
                       int  ddepth,
                       int  ksize = 1,
                       double  scale = 1,
                       double  delta = 0,
                       int  borderType = BORDER_DEFAULT 
                       )
参数的意义如下：
src---待提取边缘的图像。
dst---输出图像，与输入图像src具有相同的尺寸和通道数，数据类型由第三个参数ddepth控制。
ddepth---输出图像的数据类型(深度)。
ksize---表示Laplacian核的大小。
scale---对导数计算结果进行缩放的缩放因子，默认系数为1，不进行缩放。
delta---偏移值，在计算结果中加上偏移值。

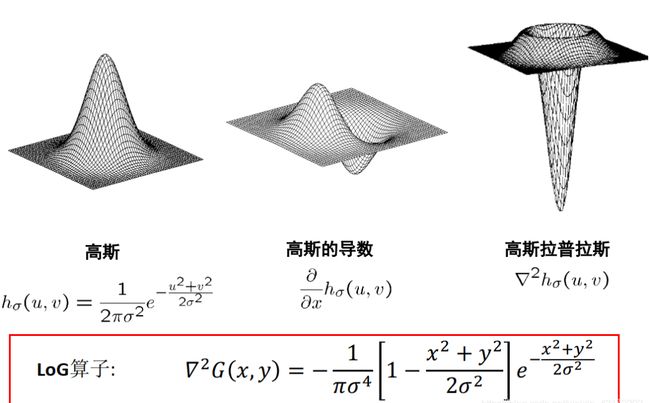
7、LoG算子边缘检测(高斯拉普拉斯)

7.1 原理

LoG边缘检测算子是David Courtnay Marr和Ellen Hildreth（1980）共同提出的。因此，也称为边缘检测算法或Marr & Hildreth算子。该算法首先对图像做高斯滤波，然后再求其拉普拉斯（Laplacian）二阶导数。即图像与 Laplacian of the Gaussian function 进行滤波运算。最后，通过检测滤波结果的零交叉（Zero crossings）可以获得图像或物体的边缘。因而，也被业界简称为Laplacian-of-Gaussian (LoG)算子。
算法描述：LoG算子也就是 Laplace of Gaussian function（高斯拉普拉斯函数）。常用于数字图像的边缘提取和二值化。LoG 算子源于D.Marr计算视觉理论中提出的边缘提取思想, 即首先对原始图像进行最佳平滑处理, 最大程度地抑制噪声, 再对平滑后的图像求取边缘。
由于噪声点（灰度与周围点相差很大的像素点）对边缘检测有一定的影响，所以效果更好的边缘检测器是LoG算子，也就是Laplacian-Gauss算子。它把的Gauss平滑滤波器和Laplacian锐化滤波器结合了起来，先平滑掉噪声，再进行边缘检测，所以效果会更好。

基于模板的LoG算子：

7.2 手工实现 LoG 算子边缘检测

//x，y方向联合实现获取高斯模板
void generateGaussMask(cv::Mat& Mask, cv::Size wsize, double sigma) {
	Mask.create(wsize, CV_64F);
	int h = wsize.height;
	int w = wsize.width;
	int center_h = (h - 1) / 2;
	int center_w = (w - 1) / 2;
	double sum = 0.0;
	double x, y;
	for (int i = 0; i < h; ++i) {
		y = pow(i - center_h, 2);
		for (int j = 0; j < w; ++j) {
			x = pow(j - center_w, 2);
			//因为最后都要归一化的，常数部分可以不计算，也减少了运算量
			double g = exp(-(x + y) / (2 * sigma * sigma));
			Mask.at(i, j) = g;
			sum += g;
		}
	}
	Mask = Mask / sum;
}


//按二维高斯函数实现高斯滤波
///
void GaussianFilter(cv::Mat& src, cv::Mat& dst, cv::Mat window) {
	int hh = (window.rows - 1) / 2;
	int hw = (window.cols - 1) / 2;
	dst = cv::Mat::zeros(src.size(), src.type());
	//边界填充
	cv::Mat Newsrc;
	cv::copyMakeBorder(src, Newsrc, hh, hh, hw, hw, cv::BORDER_REPLICATE);//边界复制

	//高斯滤波
	for (int i = hh; i < src.rows + hh; ++i) {
		for (int j = hw; j < src.cols + hw; ++j) {
			double sum[3] = { 0 };

			for (int r = -hh; r <= hh; ++r) {
				for (int c = -hw; c <= hw; ++c) {
					if (src.channels() == 1) {
						sum[0] = sum[0] + Newsrc.at(i + r, j + c) * window.at(r + hh, c + hw);
					}
					else if (src.channels() == 3) {
						cv::Vec3b rgb = Newsrc.at(i + r, j + c);
						sum[0] = sum[0] + rgb[0] * window.at(r + hh, c + hw);//B
						sum[1] = sum[1] + rgb[1] * window.at(r + hh, c + hw);//G
						sum[2] = sum[2] + rgb[2] * window.at(r + hh, c + hw);//R
					}
				}
			}

			for (int k = 0; k < src.channels(); ++k) {
				if (sum[k] < 0)
					sum[k] = 0;
				else if (sum[k] > 255)
					sum[k] = 255;
			}
			if (src.channels() == 1)
			{
				dst.at(i - hh, j - hw) = static_cast(sum[0]);
			}
			else if (src.channels() == 3)
			{
				cv::Vec3b rgb = { static_cast(sum[0]), static_cast(sum[1]), static_cast(sum[2]) };
				dst.at(i - hh, j - hw) = rgb;
			}

		}
	}

}


//DOG高斯差分
///
void DOG1(cv::Mat& src, cv::Mat& dst, cv::Size wsize, double sigma, double k = 1.6) {
	cv::Mat Mask1, Mask2, gaussian_dst1, gaussian_dst2;
	generateGaussMask(Mask1, wsize, k * sigma);//获取二维高斯滤波模板1
	generateGaussMask(Mask2, wsize, sigma);//获取二维高斯滤波模板2

	//高斯滤波
	GaussianFilter(src, gaussian_dst1, Mask1);
	GaussianFilter(src, gaussian_dst2, Mask2);

	dst = gaussian_dst1 - gaussian_dst2 - 1;

	cv::threshold(dst, dst, 0, 255, cv::THRESH_BINARY);
}



//DOG高斯差分--使用opencv的GaussianBlur

void DOG2(cv::Mat& src, cv::Mat& dst, cv::Size wsize, double sigma, double k = 1.6) {
	cv::Mat gaussian_dst1, gaussian_dst2;
	//高斯滤波
	cv::GaussianBlur(src, gaussian_dst1, wsize, k * sigma);
	cv::GaussianBlur(src, gaussian_dst2, wsize, sigma);

	dst = gaussian_dst1 - gaussian_dst2;
	cv::threshold(dst, dst, 0, 255, cv::THRESH_BINARY);
}

int main() {
	cv::Mat src = cv::imread("E:\\la.jpg");
	if (src.empty()) {
		return -1;
	}
	if (src.channels() > 1) cv::cvtColor(src, src, CV_RGB2GRAY);
	cv::Mat edge1, edge2;
	DOG1(src, edge1, cv::Size(7, 7), 2);
	DOG2(src, edge2, cv::Size(7, 7), 2);
	cv::namedWindow("src", CV_WINDOW_NORMAL);
	imshow("src", src);
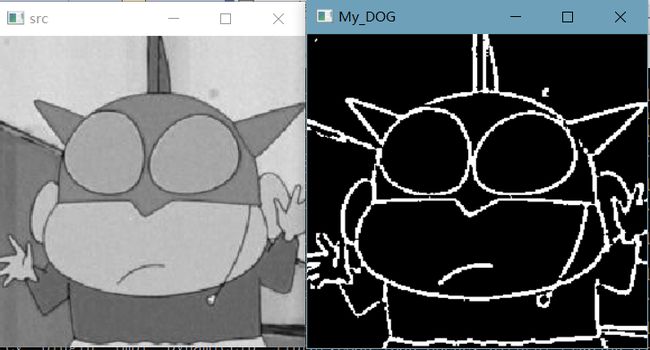
	cv::namedWindow("My_DOG", CV_WINDOW_NORMAL);
	imshow("My_DOG", edge1);

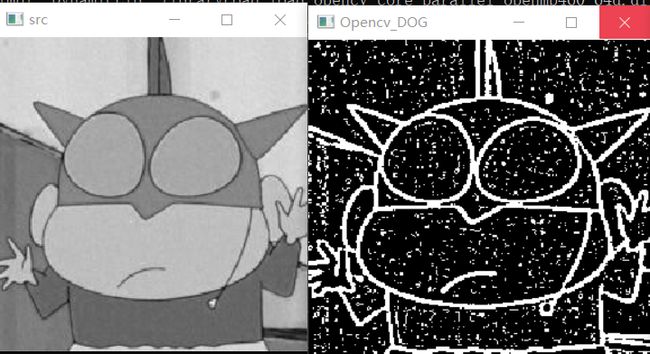
	cv::namedWindow("Opencv_DOG", CV_WINDOW_NORMAL);
	imshow("Opencv_DOG", edge2);
	cv::waitKey(0);
	return 0;

}

int main(int argc, char** argv)
{
	Mat src, gray_src, edge, LOGdst;
	src = imread("E:\\la.jpg");
	if (!src.data) {
		printf("could not load image...");
		return -1;
	}
	imshow("src", src);
	cvtColor(src, gray_src, CV_BGR2GRAY);


	Mat gauss_output, gauss_output_2;
	//定义x方向的模糊因子
	float sigma_x = 20.0;    //该参数决定了邻接像素的权重
	float sigma_y = sigma_x;
	//不同的高斯核卷积，实现了不同尺度特征，可以近似LoG
	GaussianBlur(gray_src, gauss_output, Size(3, 3), sigma_x, sigma_y);
	GaussianBlur(gray_src, gauss_output_2, Size(11, 11), sigma_x, sigma_y);

	imshow("gauss_output", gauss_output);
	//基于LoG方法
	Laplacian(gauss_output, LOGdst, -1, 3, 1.0, 0.0);
	imshow("LoGdst", LOGdst);

	//基于DoG 近似
	Mat DOGdst(src.size(), CV_32S);
	subtract(gauss_output_2, gauss_output, DOGdst);

	convertScaleAbs(DOGdst, DOGdst);
	normalize(DOGdst, DOGdst, 0, 255, NORM_MINMAX, CV_8UC1);

	imshow("DoGdst", DOGdst);
	//基于指针的操作比采用at会快一个数量级

	//基于自定义模板卷积核的实现,在经过NMS后效果或许会更好

	Mat LoG_kernel = (Mat_(5, 5) << 0, 0, -1, 0, 0,
		0, -1, -2, -1, 0,
		-1, -2, 16, -2, -1,
		0, -1, -2, -1, 0,
		0, 0, -1, 0, 0);
	Mat self_define, gauss_output2;
	GaussianBlur(gray_src, gauss_output2, Size(5, 5), 0, 0);
	filter2D(gauss_output2, self_define, CV_32FC1, LoG_kernel);
	convertScaleAbs(self_define, self_define);
	normalize(self_define, self_define, 0, 255, NORM_MINMAX, CV_8UC1);
	imshow("self_define", self_define);


	waitKey(0);
	return 0;
}

7.3 函数实现 LoG 算子边缘检测

//DOG高斯差分--使用opencv的GaussianBlur

void DOG2(cv::Mat& src, cv::Mat& dst, cv::Size wsize, double sigma, double k = 1.6) {
	cv::Mat gaussian_dst1, gaussian_dst2;
	//高斯滤波
	cv::GaussianBlur(src, gaussian_dst1, wsize, k * sigma);
	cv::GaussianBlur(src, gaussian_dst2, wsize, sigma);

	dst = gaussian_dst1 - gaussian_dst2;
	cv::threshold(dst, dst, 0, 255, cv::THRESH_BINARY);
}