- openssl+keepalived安装部署
_小亦_
项目部署keepalivedopenssl
文章目录OpenSSL安装下载地址编译安装修改系统配置版本Keepalived安装下载地址安装遇到问题安装完成配置文件keepalived运行检查运行状态查看系统日志修改服务service重新加载systemd检查配置文件语法错误OpenSSL安装下载地址考虑到后面设备可能没法连接到外网,所以采用安装包的方式进行部署,下载地址:https://www.openssl.org/source/old/
- 怎么做才能真正限制塑料袋的使用?
BalNews
Environmentalpollutionisalwaysamajorlivelihoodissue.Morethanadecadeago,ourgovernmenthadintroducedapolicyaboutrestrictionsontheuseofplasticbags,wecallitrestrictionsontheuseofplasticbags.Butmorethan10ye
- vue keep-alive
w_wx_x
作用: vue内置组件,能在组件切换过程中将状态保留在内存中,防止重复渲染DOM keep-alive是用在一个直属子组件被开关的情形,同时只有一个子组件在渲染,若有v-for则不会工作 注:keep-alive是一个抽象组件,自身不会渲染一个DOM元素,也不会出现在父组件链中//页面文件//路由exportdefaultnewRouter({routes:[{path:'/',name:'
- html 删除事件,html 事件的添加和删除
列蒂齐亚
html删除事件
jQuery在jQuery1.7版本中bind()unbind(),live()die(),on()off(),delegate()下面我们给li元素添加事件bind()旧版写法:事件不能适用脚本创建的新元素live()旧版写法:适用脚本创建的新元素写法,但性能极不好on()新版写法,事件不能适用脚本创建的新元素(接收多个函数绑定)这三种方法都是基于要给添加事件的元素本身。$("ulli").bi
- 随摘
桔桔岛
Oneshouldcaremoreaboutone'sowngrowthinsteadofothers.Toliveahappylife,oneshouldalwaystryeveryefforttominimizeregretsinlife.比起时刻注视着他人,多关注自身的成长,尽自己的一切努力让生活少点遗憾,才能过上快意人生。Whenoneshiftstheirfocusfromotherst
- 前端入门:JavaScript基础介绍
虞锦雯
一、JavaScript介绍Netscape在最初将其脚本语言命名为LiveScript,后来Netscape在与Sun合作之后将其改名为JavaScript。JavaScript最初受Java启发而开始设计的,目的之一就是“看上去像Java”,因此语法上有类似之处,一些名称和命名规范也借自Java。JavaScript与Java名称上的近似,是当时Netscape为了营销考虑与Sun微系统达成协
- Jetpack LiveData源码分析
xiangxiongfly915
#AndroidJetpack系列JetpackLiveData源码分析
文章目录JetpackLiveData源码分析前提源码分析注册订阅流程LiveData#observe()LifecycleRegistry#addObserver()ObserverWithState#dispatchEvent()LiveData#removeObserver()LiveData$LifecycleBoundObserver类LifecycleBoundObserver#sho
- Android MVVM 架构应用实现(2)
渊Y
程序员android架构
Repository类:实现BmobRepository类,作为HomeViewModel的数据提供方。BmobRepository类中有一个挂起函数getAllRecommendLibrary(libraryRecommendData:MutableLiveData)用来获取云数据库中的数据,函数的参数是LiveData,在获取数据后,利用setValue通知View展示数据。classBmob
- 前端发布 CDN缓存
跳动的世界线
前端缓存CDN
公司给服务器加了CDN,导致有时前端代码上传打包后,正式环境页面效果却不更新。每次都需要去找运维刷CDN…让我彻底记住了CDN缓存CDN(ContentDeliveryNetwork,内容分发网络)是一种广泛使用的互联网技术,旨在提高用户访问网站的速度和可靠性。CDN的核心思想是将网站的内容缓存到全球分布的边缘节点上,让用户能够从最近的节点获取数据,从而减少延迟和带宽消耗。CDN缓存机制的基本原理
- 边缘计算PCDN的使用场景及优势
神鸟云-Hu
边缘计算人工智能
一、定义PCDN,全称为PrivateContentDeliveryNetwork,即私有内容分发网络。它是一种基于P2P技术和CDN的内容分发加速网络,通过在网络中添加大量的低成本缓存服务器,将用户请求的内容从原始服务器分发到这些缓存服务器,从而实现内容更快、更稳定地传输到终端用户。二、功能PCDN的主要功能是加速内容传输。通过在CDN网络中加入更多的缓存服务器,将热点内容分布到更广泛的网络上,
- WebRTC之LiveKit的基础入门使用(入门必看)
tabzzz
前端webrtcweb3typescript
LiveKit本文主要是讲解在Next13+中如何使用LiveKit来实现简单的音视频通话,想了解更多的还是要去官方文档去掌握更复杂、高级的使用方法。什么是LiveKitLiveKit是一个开源的实时通信平台,基于WebRTC,主要用于构建高质量的音视频通话、实时数据传输和互动应用。LiveKit除了方便以外的大优势就是它提供了丰富的API和SDK,支持多种平台,包括Web、iOS、Android
- 【早安心语】
壹典心理咨询
【2021-6-9】早安春夏秋冬Nomatterhowdifficultitis,keepyourheadupstrong.Lifeisanawakening.Don’tbeyesterday,don’ttomorrow.Aslongastoday,liveinthepresentandlooktothefuture.Lifeisanattitude.Acalmmindisnaturallybro
- 浅析IM即时通讯开发中TCP协议层KeepAlive保活机制
wecloud1314
tcp/ip网络服务器
对于IM这种应用而言,应用层的网络保活的最直接办法就是心跳机制,比如主流的IM里有微信、QQ、钉钉、易信等等,可能代码实现细节有所差异,但理论上无一例外都是这样实现。(PS:没错,当初微信跟运营商间的“信令危机”就是跟这个有关)所谓的网络心跳,通常是客户端每隔一小段时间向服务器发送一个数据包(即心跳包),通知服务器自己仍然在线(心跳包中同时可能传输一些必要的数据)。发送心跳包,从通信层面来说就是为
- 准备SAP RISE Go-Live weekend
syounger
SAP项目管理制造
写本篇文章的时候,我正在等待着第一个和生产性测试(productivetest)相关的活动,财务同事下载旧生产系统的资产负债表,此份资产负债表将和新生产系统的资产负债表对比,以确保数据迁移的完整性。那么在SAPRISE项目的上线周末(Go-Liveweekend)我们需要准备点啥呢?1.上线计划(Cutoverplan)和所有SAP项目一样,上线计划是所有上线周末,包括之前和之后所有与上线相关活动
- 【大型网站技术实践】初级篇:借助LVS+Keepalived实现负载均衡
爱代码也爱生活
linux运维系统架构Keepalivedlvs
一、负载均衡:必不可少的基础手段1.1找更多的牛来拉车吧当前大多数的互联网系统都使用了服务器集群技术,集群即将相同服务部署在多台服务器上构成一个集群整体对外提供服务,这些集群可以是Web应用服务器集群,也可以是数据库服务器集群,还可以是分布式缓存服务器集群等等。古人有云:当一头牛拉不动车的时候,不要去寻找一头更强壮的牛,而是用两头牛来拉车。在实际应用中,在Web服务器集群之前总会有一台负载均衡服务
- Livewire Flash 教程
巫文钧Jill
LivewireFlash教程livewire-flashALaravelLivewire-basedFlashmessagecomponent项目地址:https://gitcode.com/gh_mirrors/li/livewire-flash项目介绍LivewireFlash是一个专为Laravel框架设计的Livewire组件,它提供了简单易用的方式来添加和显示flashed(闪烁)消息
- 周杰伦十大“冰度”歌曲
L香味
首先我个人声明,我是个04年就开始的JAY粉,榜单是我根据某狗音乐杰伦的热度榜上(live版)除外来排名的,看看你们都听过没?一、《麦烝玮》词:Jay曲:Jay麦烝玮,是经常出现在周杰伦身边的一个得力舞角,这首歌是周杰伦即兴创作歌曲,并于2011年5月18日通过小麦新浪微博首发,这歌是周杰伦写词谱曲诙谐调侃小麦。相信听过这首歌的人不会很多。二、《天台的月光》词:方文山曲:Jay《天台的月光》,作为
- Web 基础——Apache
2401_86367135
面试辅导大厂内推前端apache
EventWorker的升级版、把服务器进程和连接进行分析,基于异步I/O模型。请求过来后进程并不处理请求,而是直接交由其它机制来处理,通过epoll机制来通知请求是否完成;在这个过程中,进程本身一直处于空闲状态,可以一直接收用户请求。可以实现一个进程响应多个用户请求。并且Event模式对于Keep-Alive连接处理也有所优化,Event模式由单独的线程处理Keep-Alive长连接,执行完毕后
- 【早安心语】
壹典心理咨询
【2021-10-22】早安春夏秋冬Lifeisnoteasy,thekeytoseehowyoulive,itissaidthateveryone'slifeshouldshedthenumberoftearsisnotthesame,somepeopleathousandtears,somepeople10,000tears,somepeoplemore,thesetearscombinedh
- 【C++】CLion配置cout打印语句快捷键
全真王重阳
C++c++开发语言clioncout打印语句快捷键
点击菜单栏的File->Settings->Editor->LiveTemplates点击Define,选择C++。点击Apply和OK保存。当我们sout时,自动出现打印语句。
- JavaScript 进阶:深入探索现代编程语言的高级特性
Passion不晚
前端javascript开发语言ecmascript
JavaScript的奇妙旅程:从实验室到现代编程核心在1995年的一个夏天,Netscape的工程师BrendanEich面临一个特别的挑战:在浏览器中创建一种能让网页变得更加生动有趣的语言。当时的网页就像一张静态的海报,没有什么互动性。于是,Eich受到了一个看似简单但实际却不小的任务——开发一种新的脚本语言来填补这个空白。最终,他设计了一种名叫Mocha的语言,后来改名为LiveScript
- 极简之美:探索Minimal Linux Live的开源之旅
芮妍娉Keaton
极简之美:探索MinimalLinuxLive的开源之旅minimalMinimalLinuxLive(MLL)isatinyeducationalLinuxdistribution,whichisdesignedtobebuiltfromscratchbyusingacollectionofautomatedshellscripts.MinimalLinuxLiveoffersacoreenvi
- Android-面试-Jetpack-LiveData-你必须滴知道得知道的那些玩意儿(1)
m0_64603929
程序员面试移动开发android
作者:RicardoMJiang前言阅读本文前,大家可以先思考一些这几个问题:1.LiveData为什么可以自动取消订阅,如何避免内存泄漏?2.LiveData设置相同的值,会不会回调?3.LiveData有什么坑?如何实现LiveDataBus?带着问题学习可以让我们在学习的过程中更加有目的性与条理。例如在读源码的过程中,我们如果从头开始读,往往千头万绪,抓不住要领。而如果在开始读之前先带着几个
- 推荐:FastAPI驱动的稳定扩散LLMs演示项目
褚知茉Jade
推荐:FastAPI驱动的稳定扩散LLMs演示项目FastAPI-for-Machine-Learning-Live-DemoThisrepositorycontainsthefilestobuildyourveryownAIimagegenerationwebapplication!OutlinedarethecorecomponentsoftheFastAPIwebframework,anda
- ReactNative 常用开源组件
2401_84875852
程序员reactnative开源react.js
WebStormReactNative的代码模板插件,包括:1.组件名称2.Api名称3.所有StyleSheets属性4.组件属性https://github.com/virtoolswebplayer/ReactNative-LiveTemplateReact-native调用cordova插件https://github.com/axemclion/react-native-cordova-
- VUE3学习 第五章 Teleport传送组件、keep-alive缓存组件、transition动画组件、transition-group过度、依赖注入Provide/Inject、兄弟组件Mitt
Hyman-ya
vue3+ts+vite学习缓存javascript
一、Teleport传送组件TeleportVue3.0新特性之一。Teleport是一种能够将我们的模板渲染至指定DOM节点,不受父级style、v-show等属性影响,但data、prop数据依旧能够共用的技术;类似于React的Portal。主要解决的问题因为Teleport节点挂载在其他指定的DOM节点下,完全不受父级style样式影响1.使用方法通过to属性插入指定元素位置to=“bod
- 2023-01-09 提倡减弱户外照明灯
Eva_9c90
Outdoorlightingmakesitpossibleforhumanstosafelylivetheirliveswellaftersunset.Buttheexcessiveuseofilluminationisturningskiesoncedarkenoughtoseethousandsofstarsintoaflathaze.Andtheissuegoesfarbeyondnotb
- C++ 编程异常处理(try - throw - catch)详解
Aliven888
C/C++c++异常处理trythrowcatch
文档声明:以下资料均属于本人在学习过程中产出的学习笔记,如果错误或者遗漏之处,请多多指正。并且该文档在后期会随着学习的深入不断补充完善。感谢各位的参考查看。笔记资料仅供学习交流使用,转载请标明出处,谢谢配合。如果存在相关知识点的遗漏,可以在评论区留言,看到后将在第一时间更新。作者:Aliven888文章目录1、背景2、异常处理的概述3、异常处理的方法3.1、异常的抛出(throw)3.2、异常的检
- 速盾:虚拟主机能用cdn吗?
速盾cdn
ddos网络服务器
虚拟主机(VirtualHosting)是一种通过在一台物理服务器上划分多个虚拟服务器来提供网站托管服务的解决方案。虚拟主机被广泛应用于中小型网站,因为它具有成本低廉、易于管理的特点。然而,许多使用虚拟主机的网站可能会面临性能瓶颈和访问速度慢的问题。这时候,使用内容分发网络(ContentDeliveryNetwork,CDN)可以极大地改善网站的性能和用户体验。CDN是由分布在世界各地的服务器组
- 速盾:普通cdn和高防cdn差别在哪里?
速盾cdn
网络安全运维
CDN(ContentDeliveryNetwork)是一种通过在全球各个位置部署服务器来提供快速内容传输服务的网络架构。普通CDN和高防CDN都是CDN服务的两种类型,它们的主要差别体现在以下几个方面。首先,普通CDN和高防CDN的安全性不同。普通CDN主要用于加速内容传输,对于网络安全的防护能力较弱。而高防CDN则专注于提供更强的安全防护,包括抵御DDoS攻击、CC攻击等网络攻击形式。高防CD
- PHP,安卓,UI,java,linux视频教程合集
cocos2d-x小菜
javaUIPHPandroidlinux
╔-----------------------------------╗┆
- 各表中的列名必须唯一。在表 'dbo.XXX' 中多次指定了列名 'XXX'。
bozch
.net.net mvc
在.net mvc5中,在执行某一操作的时候,出现了如下错误:
各表中的列名必须唯一。在表 'dbo.XXX' 中多次指定了列名 'XXX'。
经查询当前的操作与错误内容无关,经过对错误信息的排查发现,事故出现在数据库迁移上。
回想过去: 在迁移之前已经对数据库进行了添加字段操作,再次进行迁移插入XXX字段的时候,就会提示如上错误。
&
- Java 对象大小的计算
e200702084
java
Java对象的大小
如何计算一个对象的大小呢?
- Mybatis Spring
171815164
mybatis
ApplicationContext ac = new ClassPathXmlApplicationContext("applicationContext.xml");
CustomerService userService = (CustomerService) ac.getBean("customerService");
Customer cust
- JVM 不稳定参数
g21121
jvm
-XX 参数被称为不稳定参数,之所以这么叫是因为此类参数的设置很容易引起JVM 性能上的差异,使JVM 存在极大的不稳定性。当然这是在非合理设置的前提下,如果此类参数设置合理讲大大提高JVM 的性能及稳定性。 可以说“不稳定参数”
- 用户自动登录网站
永夜-极光
用户
1.目标:实现用户登录后,再次登录就自动登录,无需用户名和密码
2.思路:将用户的信息保存为cookie
每次用户访问网站,通过filter拦截所有请求,在filter中读取所有的cookie,如果找到了保存登录信息的cookie,那么在cookie中读取登录信息,然后直接
- centos7 安装后失去win7的引导记录
程序员是怎么炼成的
操作系统
1.使用root身份(必须)打开 /boot/grub2/grub.cfg 2.找到 ### BEGIN /etc/grub.d/30_os-prober ### 在后面添加 menuentry "Windows 7 (loader) (on /dev/sda1)" {
- Oracle 10g 官方中文安装帮助文档以及Oracle官方中文教程文档下载
aijuans
oracle
Oracle 10g 官方中文安装帮助文档下载:http://download.csdn.net/tag/Oracle%E4%B8%AD%E6%96%87API%EF%BC%8COracle%E4%B8%AD%E6%96%87%E6%96%87%E6%A1%A3%EF%BC%8Coracle%E5%AD%A6%E4%B9%A0%E6%96%87%E6%A1%A3 Oracle 10g 官方中文教程
- JavaEE开源快速开发平台G4Studio_V3.2发布了
無為子
AOPoraclemysqljavaeeG4Studio
我非常高兴地宣布,今天我们最新的JavaEE开源快速开发平台G4Studio_V3.2版本已经正式发布。大家可以通过如下地址下载。
访问G4Studio网站
http://www.g4it.org
G4Studio_V3.2版本变更日志
功能新增
(1).新增了系统右下角滑出提示窗口功能。
(2).新增了文件资源的Zip压缩和解压缩
- Oracle常用的单行函数应用技巧总结
百合不是茶
日期函数转换函数(核心)数字函数通用函数(核心)字符函数
单行函数; 字符函数,数字函数,日期函数,转换函数(核心),通用函数(核心)
一:字符函数:
.UPPER(字符串) 将字符串转为大写
.LOWER (字符串) 将字符串转为小写
.INITCAP(字符串) 将首字母大写
.LENGTH (字符串) 字符串的长度
.REPLACE(字符串,'A','_') 将字符串字符A转换成_
- Mockito异常测试实例
bijian1013
java单元测试mockito
Mockito异常测试实例:
package com.bijian.study;
import static org.mockito.Mockito.mock;
import static org.mockito.Mockito.when;
import org.junit.Assert;
import org.junit.Test;
import org.mockito.
- GA与量子恒道统计
Bill_chen
JavaScript浏览器百度Google防火墙
前一阵子,统计**网址时,Google Analytics(GA) 和量子恒道统计(也称量子统计),数据有较大的偏差,仔细找相关资料研究了下,总结如下:
为何GA和量子网站统计(量子统计前身为雅虎统计)结果不同?
首先:没有一种网站统计工具能保证百分之百的准确出现该问题可能有以下几个原因:(1)不同的统计分析系统的算法机制不同;(2)统计代码放置的位置和前后
- 【Linux命令三】Top命令
bit1129
linux命令
Linux的Top命令类似于Windows的任务管理器,可以查看当前系统的运行情况,包括CPU、内存的使用情况等。如下是一个Top命令的执行结果:
top - 21:22:04 up 1 day, 23:49, 1 user, load average: 1.10, 1.66, 1.99
Tasks: 202 total, 4 running, 198 sl
- spring四种依赖注入方式
白糖_
spring
平常的java开发中,程序员在某个类中需要依赖其它类的方法,则通常是new一个依赖类再调用类实例的方法,这种开发存在的问题是new的类实例不好统一管理,spring提出了依赖注入的思想,即依赖类不由程序员实例化,而是通过spring容器帮我们new指定实例并且将实例注入到需要该对象的类中。依赖注入的另一种说法是“控制反转”,通俗的理解是:平常我们new一个实例,这个实例的控制权是我
- angular.injector
boyitech
AngularJSAngularJS API
angular.injector
描述: 创建一个injector对象, 调用injector对象的方法可以获得angular的service, 或者用来做依赖注入. 使用方法: angular.injector(modules, [strictDi]) 参数详解: Param Type Details mod
- java-同步访问一个数组Integer[10],生产者不断地往数组放入整数1000,数组满时等待;消费者不断地将数组里面的数置零,数组空时等待
bylijinnan
Integer
public class PC {
/**
* 题目:生产者-消费者。
* 同步访问一个数组Integer[10],生产者不断地往数组放入整数1000,数组满时等待;消费者不断地将数组里面的数置零,数组空时等待。
*/
private static final Integer[] val=new Integer[10];
private static
- 使用Struts2.2.1配置
Chen.H
apachespringWebxmlstruts
Struts2.2.1 需要如下 jar包: commons-fileupload-1.2.1.jar commons-io-1.3.2.jar commons-logging-1.0.4.jar freemarker-2.3.16.jar javassist-3.7.ga.jar ognl-3.0.jar spring.jar
struts2-core-2.2.1.jar struts2-sp
- [职业与教育]青春之歌
comsci
教育
每个人都有自己的青春之歌............但是我要说的却不是青春...
大家如果在自己的职业生涯没有给自己以后创业留一点点机会,仅仅凭学历和人脉关系,是难以在竞争激烈的市场中生存下去的....
&nbs
- oracle连接(join)中使用using关键字
daizj
JOINoraclesqlusing
在oracle连接(join)中使用using关键字
34. View the Exhibit and examine the structure of the ORDERS and ORDER_ITEMS tables.
Evaluate the following SQL statement:
SELECT oi.order_id, product_id, order_date
FRO
- NIO示例
daysinsun
nio
NIO服务端代码:
public class NIOServer {
private Selector selector;
public void startServer(int port) throws IOException {
ServerSocketChannel serverChannel = ServerSocketChannel.open(
- C语言学习homework1
dcj3sjt126com
chomework
0、 课堂练习做完
1、使用sizeof计算出你所知道的所有的类型占用的空间。
int x;
sizeof(x);
sizeof(int);
# include <stdio.h>
int main(void)
{
int x1;
char x2;
double x3;
float x4;
printf(&quo
- select in order by , mysql排序
dcj3sjt126com
mysql
If i select like this:
SELECT id FROM users WHERE id IN(3,4,8,1);
This by default will select users in this order
1,3,4,8,
I would like to select them in the same order that i put IN() values so:
- 页面校验-新建项目
fanxiaolong
页面校验
$(document).ready(
function() {
var flag = true;
$('#changeform').submit(function() {
var projectScValNull = true;
var s ="";
var parent_id = $("#parent_id").v
- Ehcache(02)——ehcache.xml简介
234390216
ehcacheehcache.xml简介
ehcache.xml简介
ehcache.xml文件是用来定义Ehcache的配置信息的,更准确的来说它是定义CacheManager的配置信息的。根据之前我们在《Ehcache简介》一文中对CacheManager的介绍我们知道一切Ehcache的应用都是从CacheManager开始的。在不指定配置信
- junit 4.11中三个新功能
jackyrong
java
junit 4.11中两个新增的功能,首先是注解中可以参数化,比如
import static org.junit.Assert.assertEquals;
import java.util.Arrays;
import org.junit.Test;
import org.junit.runner.RunWith;
import org.junit.runn
- 国外程序员爱用苹果Mac电脑的10大理由
php教程分享
windowsPHPunixMicrosoftperl
Mac 在国外很受欢迎,尤其是在 设计/web开发/IT 人员圈子里。普通用户喜欢 Mac 可以理解,毕竟 Mac 设计美观,简单好用,没有病毒。那么为什么专业人士也对 Mac 情有独钟呢?从个人使用经验来看我想有下面几个原因:
1、Mac OS X 是基于 Unix 的
这一点太重要了,尤其是对开发人员,至少对于我来说很重要,这意味着Unix 下一堆好用的工具都可以随手捡到。如果你是个 wi
- 位运算、异或的实际应用
wenjinglian
位运算
一. 位操作基础,用一张表描述位操作符的应用规则并详细解释。
二. 常用位操作小技巧,有判断奇偶、交换两数、变换符号、求绝对值。
三. 位操作与空间压缩,针对筛素数进行空间压缩。
&n
- weblogic部署项目出现的一些问题(持续补充中……)
Everyday都不同
weblogic部署失败
好吧,weblogic的问题确实……
问题一:
org.springframework.beans.factory.BeanDefinitionStoreException: Failed to read candidate component class: URL [zip:E:/weblogic/user_projects/domains/base_domain/serve
- tomcat7性能调优(01)
toknowme
tomcat7
Tomcat优化: 1、最大连接数最大线程等设置
<Connector port="8082" protocol="HTTP/1.1"
useBodyEncodingForURI="t
- PO VO DAO DTO BO TO概念与区别
xp9802
javaDAO设计模式bean领域模型
O/R Mapping 是 Object Relational Mapping(对象关系映射)的缩写。通俗点讲,就是将对象与关系数据库绑定,用对象来表示关系数据。在O/R Mapping的世界里,有两个基本的也是重要的东东需要了解,即VO,PO。
它们的关系应该是相互独立的,一个VO可以只是PO的部分,也可以是多个PO构成,同样也可以等同于一个PO(指的是他们的属性)。这样,PO独立出来,数据持
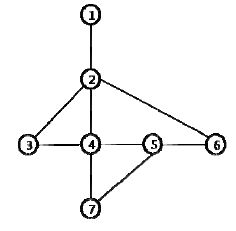
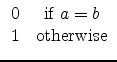
![]() n1
n1![]() 100, 2
100, 2![]() n2
n2![]() 4, 950) <tex2html_verbatim_mark>where n1 <tex2html_verbatim_mark>is the number of vertices of the graph representing the working map of a salesman and n2 <tex2html_verbatim_mark>is the number of edges in the graph. The input graph is a connected graph. Each vertex of the graph is numbered from 1 to n1 <tex2html_verbatim_mark>. In the following n2 <tex2html_verbatim_mark>lines, each line contains a pair of vertices which represent an edge of the graph. The last line of each test case contains information on a working path of the salesman. The first integer n <tex2html_verbatim_mark>(2
4, 950) <tex2html_verbatim_mark>where n1 <tex2html_verbatim_mark>is the number of vertices of the graph representing the working map of a salesman and n2 <tex2html_verbatim_mark>is the number of edges in the graph. The input graph is a connected graph. Each vertex of the graph is numbered from 1 to n1 <tex2html_verbatim_mark>. In the following n2 <tex2html_verbatim_mark>lines, each line contains a pair of vertices which represent an edge of the graph. The last line of each test case contains information on a working path of the salesman. The first integer n <tex2html_verbatim_mark>(2![]() n
n![]() 200) <tex2html_verbatim_mark>in the line is the length of the path and the following n integers represent the sequence of vertices in the working path.
200) <tex2html_verbatim_mark>in the line is the length of the path and the following n integers represent the sequence of vertices in the working path.
