概率论与数理统计学习笔记（6）——分布律，分布函数，密度函数

对了宝贝儿们，卑微小李的公众号【野指针小李】已开通，期待与你一起探讨学术哟~摸摸大！

1 离散型随机变量

离散型随机变量指的是取到的值时有限个或者可列无限多个的随机变量。有限个值很好理解，但是可列无限多个值就有点抠脑壳。这句话的含义就是尽管变量有无限多个，但是我们可以按照一定的词序一一列举出来。我这里举两个例子来说明。

E1：$X=x_k(k=1,2,\dots )$
E2: 反复投掷硬币，记录出现第一次正面朝上需要的次数。
我们将E2绘制成表格：

Table 1. 反复抛掷硬币，记录出现第一次正面朝上需要的次数

次数	发生该次数的概率
1	$1/2$
2	$1/4$
3	$1/8$
4	$1/16$
5	$1/32$
$⋮$	$⋮$

根据上表，我们可以发现尽管该事件有无限多个随机变量，但是我们都可以一一列举出来。接着我们还可以发现，我们只要知道离散型随机变量$X$的所有可能取值以及取每一个值的概率，就可以掌握$X$的统计规律。

形式化表达则是，设离散型随机变量$X$所有可能的取值为$x_k(k=1,2,\dots )$，$X$取各个值的概率，即事件$\{X=x_k\}$的概率为：
$$P\{X=x_k\}=p_k,k=1,2,\dots$$

由于这是概率，所以满足：

1. $p_k\ge 0,k=1,2,\dots$
2. ${\sum }_{k=1}^{\infty }{p}_k=1$

换句话说就是：

1. $X$所有可能取值的概率大于等于0.
2. 所有事件发生的概率之和为1.

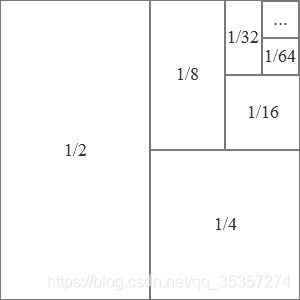
就比如表1，我们以分布律来直观的看这些数据：

Table 2. 第一次正面朝上需要的次数的分布律

$X$	1	2	3	4	5	$\dots$
$p_k$	$1/2$	$1/4$	$1/8$	$1/16$	$1/32$	$\dots$

就是说$P\{X=1\}=\frac{1}{2}$。其概率之和为1直观的表示如下图：

Fig. 1. 无限个离散随机变量概率之和为1

1.1 （0-1）分布

设随机变量$X$只有0和1两个值，其分布律为

$$P\{X=k\}=p^k(1-p{)}^{1-k},k=0,1(0<p<1)，$$
则称$X$服从以$p$为参数的（0-1）分布或两点分布。其分布律为：

Table 3. （0-1）分布分布律

$X$	0	1
$p_k$	$1-p$	$p$

就是说一个事件只有两种可能的结果，在一次实验中有$p$的概率发生1，$1-p$的概率发生0.

1.2 伯努利试验

伯努利试验指的是试验$E$只有两个可能的结果$A$与$\bar{A}$。其中$P(A)=p(0<p<1)$，$P(\bar{A})=1-p$。如果独立重复（试验互不干扰，且$P(A)=p$不变）进行$n$次试验，则称这一组试验为$n$重伯努利试验。

因为独立，所以假设$C_i$为第$i$次试验的结果（$C_i$为$A$或$\bar{A}$，$i=1,2,\dots ,n$），则：

$$P(C_1{C}_2\dots C_n)=P(C_1)P(C_2)\dots P(C_n)$$

由此可见，（0-1）分布就是$n=1$的伯努利试验。

1.3 二项分布

那么当$n>1$时，以$X$表示$n$重伯努利试验中事件$A$发生的次数，假定事件$A$发生$k(0\le k\le n)$次，$\bar{A}$发生$n-k$次。于是在$n$次试验中，$A$发生$k$次的概率为：

$$P\{X=k\}={\mathrm{C}}_n^k{p}^k(1-p{)}^{n-k},k=0,1,2,\dots ,n$$

该公式就是说事件$A$发生了$k$次，事件$\bar{A}$发生了$n-k$次。由于有多次试验，每次试验都会有两种结果，所以将所有可能性给组合起来，就有了最前面的${\mathrm{C}}_n^k$。

1.4 几何分布

几何分布指的是在$n$重伯努利试验中，试验$k$次事件才发生的概率。与二项分布不同的一点就在于，二项分布是$A$发生了$k$次，$\bar{A}$发生了$n-k$次；而几何分布是试验了$k$次后，事件$A$才发生。

几何分布的分布率为：

$$P(X=k)=(1-p{)}^{k-1}p,(0<p<1),k=1,2,\dots$$

1.5 泊松分布

关于泊松分布，《如何通俗理解泊松分布？》这篇博客讲的就很详细生动了，这里我也就不多赘述。就只谈谈我个人的看法。

根据这个大佬的讲解，泊松分布就是将一个区间给等分为无限细的小区间，且任意两个区间上事件是独立的且发生的概率相等，求解事件发生$1,2,\dots$次的概率。其计算过程就是通过求一个极限的泰勒展开而得到的公式。其概率密度函数为：

$$P(X=k)=\frac{{\lambda }^k{\mathrm{e}}^{-\lambda }}{k!},k=0,1,2,\dots$$

由于泊松分布的均值$\mu =\lambda$，所以在这里$\lambda$反映了分布的强度，就是反映了整个区间上的平均程度。

由于二项分布中$p$很小时，泊松分布与二项分布很接近，所以我将泊松分布简单的理解为：反映了在一个无限窄的区间上，事件发生的可能性很小的情况下，事件发生次数的概率。

2. 连续型随机变量

离散型随机变量是我们可以列举出来的，但是对于连续型随机变量，我们是无法列举出来。同时，连续型随机变量在某一点的概率为0。所以我们有必要讨论连续型随机变量。

关于连续型随机变量在某一点概率为0，其有两种思考方式。

1. 由于概率可以用面积表示，所以我们可以用几何的方式来理解这一点。
   
   我们若要计算阴影部分面积，只需要计算$(0.3-0)\times 1$即可得到。但是对于某一点（假设$x=0.3$），那么图就变为了如下：
   
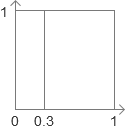
   由于线段没有长度，或者说长度无限小，那么这个面积也就为0，即概率为0.
2. 从微积分的角度考虑，计算某一点的概率，就等于在这个点周围取了一个无限小的数$\Delta x\to 0$，计算这个区间的概率。那么可以得到如下的等式：
   $$0\le P\{X=a\}\le P\{a-\Delta x<X\le a\}=F(a)-F(a-\Delta x)$$
   由于$\Delta x\to 0$，所以$F(a)-F(a-\Delta x)\to 0$，近似可得$0\le P\{X=a\}\le 0$，于是$P\{X=a\}=0$。

2.1 分布函数与概率密度函数

在详细讲解分布函数与概率密度函数之前，先谈谈我对这两个函数的理解，再做展开。

1. 分布函数$F(x)$刻画的是区间$(-\infty ,x]$内发生事件的概率。
2. 概率密度函数$f(x)$刻画的是在$x$附近的值出现的概率。

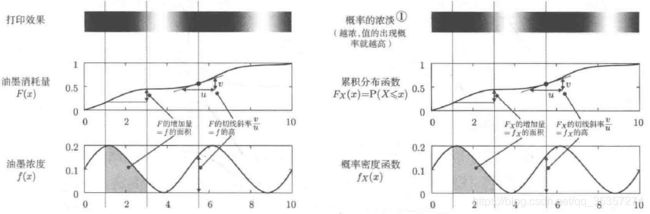
关于分布函数与概率密度函数，我们借用[2]中129页的图来说明。

Fig. 2. 打印至x处时消耗的油墨量F(x)与浓度f(x)的关系[2]

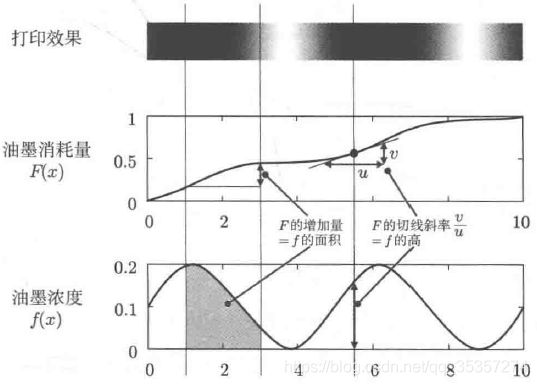
这张图简单来说，就是需要打印一份渐进变色的纸，其油墨消耗量为$F(x)$，油墨浓度为$f(x)$。由于打印的过程中需要消耗油墨，油墨消耗量的增多必定伴随着在纸张上打印，而打印所消耗的油量等于这段时间打印的长度乘以这段时间机器出的油墨浓度。形式化表达为：

$$\mathrm{d}F(x)=f(x)\mathrm{d}x$$
其中，$\mathrm{d}x$代表在纸张上移动的距离（极短距离），$f(x)$代表在这极短距离内的出墨量（由于距离很短，所以可以近似看做出墨量在图形中表现为一个矩形），$\mathrm{d}F(x)$代表这段时间油墨消耗量增加了多少。由此可见，这就是一个微积分的问题，即：
$$f(x)=\frac{\mathrm{d}F(x)}{\mathrm{d}x}$$
或者说
$${\int }_a^{b}f(x)\mathrm{d}x=F(b)-F(a)$$

我们通过这个例子，推广到分布函数与概率密度函数：

Fig. 3. 打印问题与概率问题的对比[2]

那么我们同样采用油量问题来推理这个问题，分布函数代表了区间内事件发生的概率之和，概率密度函数代表了在某个点周围事件发生的概率大小。

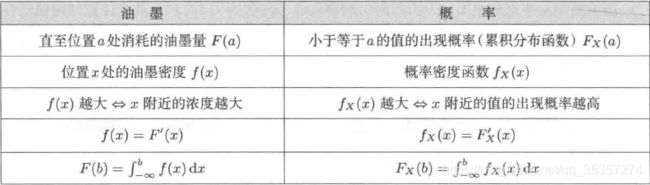
两者的关系绘制成表格如表4所示：

Fig. 4. 打印问题与概率问题的对应关系[2]

同时，我们可以获得概率密度$f(x)$的性质：

1. $f(x)\ge 0$;
2. ${\int }_{-\infty }^{\infty }f(x)\mathrm{d}x=1$;
3. 对于任意实数$x_1$，$x_2(x_1\le x_2)$，有
   $$P\{x_1<X\le x_2\}=F(x_2)-F(x_1)={\int }_{x_1}^{x_2}f(x)\mathrm{d}x;$$
4. 若$f(x)$在点$x$处连续，则有$F^{\prime }(x)=f(x)$

对于性质2，我们知道$f(x)=\frac{\mathrm{d}F(x)}{\mathrm{d}x}$，反映的就是在微小变化下$F(x)$的变化，又由于$F(x)$最大为1，所以${\int }_{-\infty }^{\infty }f(x)\mathrm{d}x=1$。

2.2 均匀分布

均匀分布的图如4所示。

Fig. 5. 均匀分布

从图中我们可以看出，均匀分布的核心就在于均匀上，区间$[a,b]$中任意一段区间$[\alpha ,\beta ]$的概率都为$\frac{\beta -\alpha }{b-a}$。

其概率密度表达为：

$$\begin{array}{r}f(x)=\{\begin{array}{rlr}& \frac{1}{b-a}& (a\le b),\\ & 0& 其他\end{array}\end{array}$$
如果连续型随机变量$X$具有这样的密度函数，则称$X$在区间$[a,b]$上服从均匀分布，$X\sim U(a,b)$。

其分布函数为：

$$\begin{array}{r}f(x)=\{\begin{array}{rlrl}& 0,& & x<a,\\ & \frac{1}{b-a}& & (a\le b),\\ & 1& & x\ge b.\end{array}\end{array}$$

分布函数图像为：

Fig. 6. 均匀分布分布函数

2.3 指数分布

指数分布是几何分布的连续型表达，关注的也是事件$A$第一次发生的概率，以及发生前等待的时间。由于泊松分布关注的是时间段内$A$发生的次数，而指数分布关注的是第一次发生的时间，那么也就是说可以等价考虑为只用计算泊松分布中事件发生0次的概率，再减去这个概率。

我们将$k=0$代入泊松分布中，得到：

$$P(X=0,x)=\frac{(\lambda x{)}^0{\mathrm{e}}^{-\lambda x}}{0!}=e^{-\lambda x}$$

这是事件没有发生的概率，$1-P(X=0,x)$得到的是事件第一次发生的概率。对其求导可得：

$$f(x)=\{\begin{array}{rlrl}& \lambda e^{-\lambda x},& & x>0\\ & 0,& & 其他\end{array}$$

这个就是参数为$\frac{1}{\lambda }$的指数分布。

而指数函数有个重要的性质，就是无记忆性，即对于任意的$s,t>0$，有：
$$P\{X>s+t|X>s\}=P\{X>t\}$$

这个公式推导参考[1]的45页。直观理解就是，有个灯泡平均5分钟闪一次，我等了10分钟还没有闪，那么它下一次闪还是要再平均等5分钟（预期时间不会因为等待长短而改变）[6]。就是说过去的影响不到未来的事情。

2.4 正态分布

正态分布是常用的一种分布，就比如神经网络初始权重分配的时候都可以采用随机正态分布进行赋值。其特点是左右对称，且中心概率密度高，边缘概率密度低。由于其推导过程我感觉有点复杂，就没有深入研究，这里就只介绍其性质。

2.4.1 标准正态分布

标准正态分布的概率密度函数为：
$$f(x)=\frac{1}{\sqrt{2\pi }}{\mathrm{e}}^{-\frac{x^2}{2}}$$

由于$\frac{1}{\sqrt{2\pi }}$和$\frac{1}{2}$都是常量，所以可以将上式粗略的看成是：

$$f(x)=C_1{\mathrm{e}}^{-C_2{x}^2}$$
其中$C_1$和$C_2$代表上面提到的两个常量。由此我们可以发现，这是一个关于${\mathrm{e}}^{-x^2}$的函数。其函数图像如下：

这个图片是由下代码生成的：

xs = np.arange(-5, 6, 0.1)
y = []
for x in xs:
    y.append(math.exp(-x**2))
    
plt.plot(xs, y)
plt.show()

那么我们就可以得到${\mathrm{e}}^{-x^2}$的性质：

1. 左右关于$x=0$对称。
2. 在$x=0$处取得最大值。
3. 随着$x$与0的差值越来越大，值越来越小。
4. 当$x\to -\infty$或$x\to \infty$时，$y\to 0$。

由于$C_1$与$C_2$为常数项，所以$f(x)$的性质与上面的内容相同。

2.4.2 一般正态分布

接着我们对标准正态分布进行平移或缩放后，即可获得一般正态分布。通过定义两个常量$\mu$与$\sigma$来实现。

1. 平移$\mu$：$Y\equiv Z+\mu$
2. 缩放$\sigma$倍：$W\equiv \sigma Z(\sigma >0)$
3. 缩放$\sigma$倍后平移$\mu$：$X\equiv \sigma Z+\mu$

其变换图像如图7所示：

Fig. 7. 标准正态分布与一般正态分布的转换[2]

根据图我们就会发现，上面4条性质变成了：

1. 左右关于$x=\mu$对称。
2. 在$x=\mu$处取得最大值。
3. 随着$x$与$\mu$的差值越来越大，值越来越小。
4. 当$x\to -\infty$或$x\to \infty$时，$y\to 0$。

而变换后$X$的期望与方差变为了：

$$E[X]=E[\sigma Z+\mu ]=\sigma E[Z]+\mu =\mu$$

$$V[X]=V[\sigma Z+\mu ]={\sigma }^{2}V[Z]={\sigma }^2$$

这里有这个等式，是因为标准正态分布的$E[Z]=\mu =0,V[Z]={\sigma }^2=1$。

于是一般正态分布的概率密度函数为：

$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }\mathrm{e}\mathrm{x}\mathrm{p}(-\frac{(x-\mu {)}^2}{2{\sigma }^2}),(-\infty <x<\infty )$$

References

[1] 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 第四版. 北京: 高等教育出版社, 2009.
[2] 平冈和幸, 堀玄. 程序员的数学2概率统计[M]. 北京: 人民邮电出版社, 2015.
[3] 3Blue1Brown. 【官方双语/合集】微积分的本质 - 系列合集[EB/OL]. (2018-06-03)[2021-05-28]. https://www.bilibili.com/video/BV1qW411N7FU
[4] 马同学图解数学. 如何通俗理解泊松分布？[EB/OL]. (2019-04-12)[2021-05-28]. https://blog.csdn.net/ccnt_2012/article/details/81114920
[5] 知乎. 指数分布公式的含义是什么？[EB/OL]. [2021-05-28]. https://www.zhihu.com/question/24796044/answer/1873495709
[6] 陈伟华. 如何理解指数分布的无记忆性？ [EB/OL]. (2020-08-04)[2021-05-28]. https://www.zhihu.com/question/36965252