皮尔逊/斯皮尔曼相关系数
相关系数
- 1.相关性的直观展示
- 2.斯皮尔曼等级相关系数 (Spearman's Rank Correlation Coefficient)
-
- 2.1 定义
- 2.2 示例
- 3.皮尔逊相关系数(Pearson Correlation Coefficient)
-
- 3.1 计算公式
- 3.2 皮尔逊相关系数与余弦相似度
- 参考文献
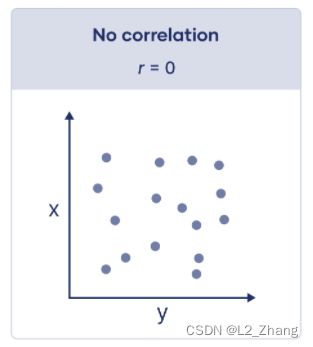
1.相关性的直观展示
以上各图来自https://www.scribbr.com/statistics/pearson-correlation-coefficient/。
2.斯皮尔曼等级相关系数 (Spearman’s Rank Correlation Coefficient)
2.1 定义
斯皮尔曼等级相关系数是一种衡量两个变量X、Y相关性的方法。
计算公式为:
ρ = 1 − 6 ∑ d i 2 n 3 − n \qquad\qquad \rho=1-\cfrac{6\sum d_i^2}{n^3-n} ρ=1−n3−n6∑di2,其中 d i = x i − y i d_i=x_i-y_i di=xi−yi。
有趣的是,它不是直接针对变量各维度的值进行运算,而是针对各维度值的排序,即所谓的等级(rank)。
显然,如果两变量单调性一致,则各维度等级的差 d i d_i di均为0时, ρ = 1 \rho=1 ρ=1;单调性相反时, ρ = − 1 \rho=-1 ρ=−1。
2.2 示例
引自wiki百科–Spearman’s rank correlation coefficient中的例子,计算IQ值与每周看电视小时数之间的斯皮尔曼相关系数:

其计算过程也非常简单:
- 对X中各数据进行排序,获得rank x i x_i xi;
- 对Y中各数据进行排序,获得rank y i y_i yi;
- 对应求得 d i = x i − y i d_i=x_i-y_i di=xi−yi,同时计算平方值 d i 2 d_i^2 di2;
- 求得 ∑ d i 2 \sum d_i^2 ∑di2,并计算 ρ = 1 − 6 ∑ d i 2 n 3 − n \rho=1-\cfrac{6\sum d_i^2}{n^3-n} ρ=1−n3−n6∑di2。
此例子中计算的 ρ \rho ρ为 − 0.176 -0.176 −0.176,接近于0 ,略显负相关,即智商较低的人,看电视时间较长。
3.皮尔逊相关系数(Pearson Correlation Coefficient)
皮尔逊相关系数取值范围也是[-1,1]。
3.1 计算公式
皮尔逊相关系数的几个等价公式:
ρ X , Y = c o v ( X , Y ) σ X σ Y = E [ ( X − μ X ) ( Y − μ Y ) ] σ X σ Y \rho_{X,Y}=\cfrac{cov(X,Y)}{\sigma_X \sigma_Y}=\cfrac{E[(X-\mu_X)(Y-\mu_Y)]}{\sigma_X \sigma_Y} ρX,Y=σXσYcov(X,Y)=σXσYE[(X−μX)(Y−μY)]
ρ X , Y = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 ∑ i = 1 n ( y i − y ˉ ) 2 = n ∑ x i y i − ∑ x i ∑ y i n ∑ x i 2 − ( ∑ x i ) 2 n ∑ y i 2 − ( ∑ y i ) 2 \rho_{X,Y}=\cfrac{\sum\limits_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{{\sum\limits_{i=1}^n(x_i-\bar{x}} )^2}\sqrt{{\sum\limits_{i=1}^n(y_i-\bar{y}} )^2}}\\ \\ \quad\quad\ = \cfrac{n\sum x_iy_i-\sum x_i \sum y_i}{\sqrt{n \sum x_i^2-(\sum x_i)^2}\sqrt{n \sum y_i^2-(\sum y_i)^2}} ρX,Y=i=1∑n(xi−xˉ)2i=1∑n(yi−yˉ)2i=1∑n(xi−xˉ)(yi−yˉ) =n∑xi2−(∑xi)2n∑yi2−(∑yi)2n∑xiyi−∑xi∑yi
3.2 皮尔逊相关系数与余弦相似度
设向量 x = { x 1 , x 2 , . . . , x n } , y = { y 1 , y 2 , . . . , y n } x=\{x_1,x_2,...,x_n\},y=\{y_1,y_2,...,y_n\} x={x1,x2,...,xn},y={y1,y2,...,yn},则二者的余弦相似度定义为:
cos θ = x y ∣ x ∣ ∣ y ∣ = ∑ x i y i ∑ x i 2 ∑ y i 2 \qquad\qquad\qquad\cos\theta=\cfrac{xy}{|x||y|}=\cfrac{\sum x_i y_i}{\sqrt{\sum x_i^2\sqrt{\sum y_i^2}}} cosθ=∣x∣∣y∣xy=∑xi2∑yi2∑xiyi。
因此当 x ˉ = y ˉ = 0 \bar{x}=\bar{y}=0 xˉ=yˉ=0时,二者计算一致。
参考文献
[1]Pearson Correlation Coefficient
[2] Spearman correlation coefficient: Definition, Formula and Calculation with Example
[3] wiki–Spearman’s rank correlation coefficient
[4] https://www.scribbr.com/statistics/pearson-correlation-coefficient/