内功心法：深入研究整型数（下）

本文分为上下两篇

上文提到了终极三问：
为什么两个较大数之和为一个较小数？
为什么两个正数之和为负数？
为什么正数比负数小？

为了解答这三个问题，我们继续修行内功！继续研究一下整型数！

1.无符号数和有符号数的截断

在很多应用中，需要将一个较大的数据类型转换成一个较小的数据类型，这种转换过程称为截断。对于无符号数和有符号数截断操作会直接将高位丢弃，会改变数据的数值，也会改变数据的位级表示。

截断示例程序如下：

#include

int main()
{
	unsigned int  un_num = 1004;
	signed int    num = -1004;
	
	unsigned char un_truncation = (unsigned int ) un_num;
	signed char   truncation = (int)num;
	printf("truncation = %d , un_truncation = %u , un_num = %x , num = %x \n", truncation , un_truncation ,un_num , num);

	return 0;
}

运行结果如下：

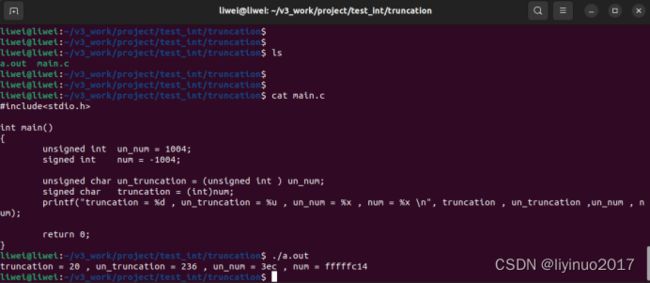
示例分析
无符号数un_num（1004） 的二进制表示为0x3ec ,数据截断为1字节后的二进制表示为0xec（236）。因此无符号数截断操作会直接将高位丢弃，会改变数值，也会改变位级表示。
有符号数num （-1004）的二进制表示为0xfffffc14 ,数据截断为1字节后的二进制表示为0x14（20）。因此有符号数截断操作会直接将高位丢弃，会改变数值，也会改变位级表示。

总结：
对于无符号数和有符号数截断操作会直接将高位丢弃，截断操作会改变数据的数值，也会改变数据的位级表示。

2.整型数运算

整数由无符号数和有符号数组成，整数运算偶尔会出现以下情况：

1、两个较大数之合为一个较小数。
2、两个正数之合为负数。
3、正数比负数小。

我们将深入学习一下整数的运算原理，并一一解答这3个问题。

2.1无符号数加法

假设两个n位无符号数X和Y满足：

这两个数之合的范围为：


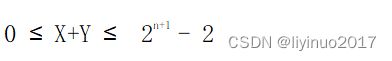
的范围超出了n位无符号数的范围，这种情况下将丢弃权重大于n的位。

两个n位无符号数X和Y加法原理如下：

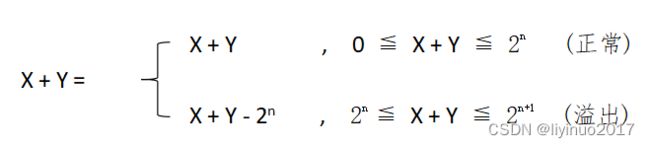
溢出是指的完整的整数结果不能放到数据类型的字长限制中去，这种情况下将丢弃超出字长限制的位。
以4位无符号数加为例：

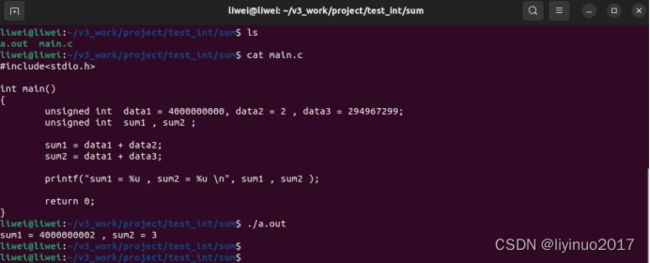
无符号数加法示例程序如下：

#include

int main()
{
	unsigned int  data1 = 4000000000, data2 = 2 , data3 = 294967299;
	unsigned int  sum1 , sum2 ;
	
	sum1 = data1 + data2;
	sum2 = data1 + data3;

	printf("sum1 = %u , sum2 = %u \n", sum1 , sum2 );

	return 0;
}

运行结果如下：

由运行结果可知：

sum1 = 4000000000 + 2 = 4000000002， 结果正确 。
sum2 = 4000000000 + 294967299= 3 ，结果溢出。
sum2 为32位数（0位~31位），丢弃结果超出字长限制的位（第32位），这种运算类似模运算。

这就解释了终极三问中的：为什么两个较大数之和为一个较小数？

无符号数加法溢出往往会造成不可预料的后果，因此我们需要检查运算是否溢出，无符号数加法溢出检查原理如下：

假设有两无符号数X和Y , Z = X+ Y， 当 Z < X 或者Z < Y时，发生了溢出。

2.2有符号数加法

有符号数在计算机中以补码的形式存在，两个n位有符号数X和Y加法原理如下：

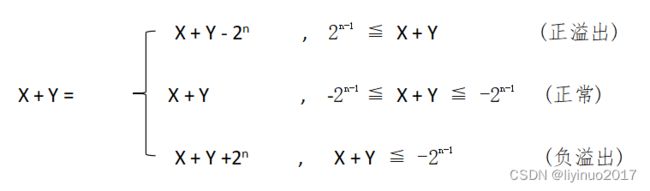
由公式可知两个n位有符号数相加时，当X+Y值大于等于2的（n-1）次方 时发生了正溢出，此时结果变为一个负数；当 X + Y 小于等于负的2的（n-1）次方时发生负溢出，此时的结果变为一个正数。
以4位有符号数加为例：

有符号数加法示例程序如下：

#include

int main()
{
	char  data1 = 70, data2 = 70 , data3 = -80, data4 = -80;
	char  sum1 , sum2;	
	
	sum1 = data1 + data2;
	sum2 = data3 + data4;

	printf("sum1 = %d , sum2 = %d \n", sum1 , sum2 );

	return 0;
}

示例程序运行结果如下：

由实验结果可知： 70 +70的结果为-116， -80 + （-80）的结果为96。

运算分析：
70的二进制值为0x46 , 70 +70 的二进制结果为0X8c (140) , 0X8c表示的补码值为-116 。
由此可见，计算机用两个二进制数做计算，并不判断这个数是否是补码，一视同仁的进行计算，只是在输出的时间，根据不同的要求解释成不同的值。如0X8c可以被解释成140，也可以解释成-116。

这里回答了终极三问中：为什么两个正数之和为负数？

2.3有符号数和无符号数比较

在很多编程标准和规范中都规定了，有符号数和无符号数不能比较大小，往往会出现负数大于正数。
有符号数和无符号数比较大小示例程序如下：

#include

int main()
{
	int  data1 = -3 ;
	unsigned int data2 = 80;	
	
	printf("data1 = %x ,data2 =%x \n" , data1 ,data2);
	
	if(data1 > data2)
	{
		printf("  %d big than  %d\n", data1 , data2);
	}
	else
	{		
		printf(" %d big than  %d\n", data2 , data1);
	}

	return 0;
}

示例程序运行结果如下：

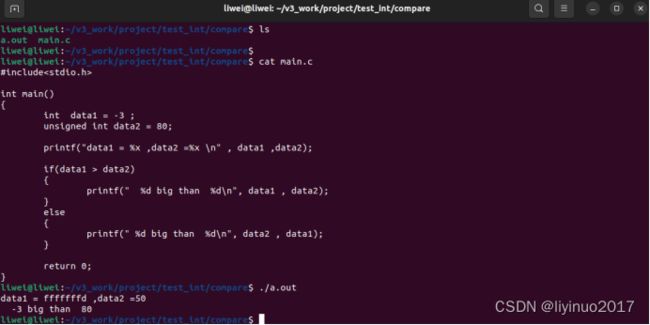
分析运行结果：
在比较大小时计算器认为-3大于80 ，原因是负数是以补码形式存在，计算机在比较-3和80这两个数时，直接将这两个数的二进制值0xfffffffd(-3)和0x00000050(80)进行比较，很显然计算器认为0xfffffffd更大。

这里回答了终极三问中：为什么正数比负数小？

所以我们编程要符合规定，不能用有符号和无符号数直接比较大小。

3.总结

综上所述我们来总结一下：
1、位级表示
编译器在编译程序时，用二进制补码形式表示负数，用传统二进制形式表示正数。代码在机器中运行时，负数以二进制补码形式存在，正数以传统二进制形式存在。

例如：负数-3在计算机中以0xfffffffd二进制形式存在，正数80在计算器中以0x00000050二进制形式存在。

2、位级运算
计算机在运算时，不判断对象是否是负数（补码）还是正数，直接用二进制数去作计算。

例1：-3 + 80 = 0xfffffffd + 0x00000050 = 0x0000004d (高位溢出) = 77
例2：-3 比较 80 = 0xfffffffd 比较 0x00000050 = 0xfffffffd > 0x00000050 = -3 >80

3、位级显示
在输出数据时，计算机会根据用户设置的类型，将二进制数解释成相应的值，同一个二进制值，不同的解释可能有不同的数值。

例如：二进制值为0xfffffffd ，用户认为这个数是一个有符号数printf 用%d 格式输出时，计算器会将这个数解释成-3；当用户认为这个数是一个有符号数printf 用%u 格式输出时计算器会将这个数解释成4294967293 。

创作不易希望朋友们点赞，转发，评论，关注。
您的点赞，转发，评论，关注将是我持续更新的动力
作者：李巍
Github：liyinuoman2017
CSDN：liyinuo2017
今日头条：程序猿李巍