基于差异演化的寄生樽海鞘群算法
文章目录
- 一、理论基础
-
- 1、标准SSA算法
- 2、PDESSA算法
-
- 2.1 改进领导者全局搜索方式
-
- 2.1.1 上代领导者位置信息的影响
- 2.1.2 非线性惯性权重
- 2.2 寄生和宿主双种群
- 2.3 PDESSA算法伪代码
- 二、仿真实验与结果分析
- 三、参考文献
一、理论基础
1、标准SSA算法
请参考这里。
2、PDESSA算法
2.1 改进领导者全局搜索方式
2.1.1 上代领导者位置信息的影响
在标准SSA的整个迭代过程中,占种群个体数量 1 / 2 1/2 1/2的领导者,都是直接奔向当前全局最优解位置(食物源)的,这种位置更新方式会导致算法搜索过程中跳跃性过强,执行全局搜索的领导者多样性较低,难以保证全局空间中搜索的充分性和完备性,易早熟收敛和滞困于局部最优.针对这一问题,本文将上轮迭代中对应的领导者信息引入领导者更新公式,使领导者既受到全局最优解的影响,又与上轮进化结果相关联,既分享了整个樽海鞘群的全局进化成果,也保留了每个领导者的个体进化印记,从而提升了算法跳出局部极值区域找到全局最优的能力。改进后的领导者位置更新公式为: X j i ( t ) = X j i ( t − 1 ) + ( F o o d P o s i t i o n j ( t − 1 ) − X j i ( t − 1 ) ) × r a n d (1) X_j^i(t)=X_j^i(t-1)+(FoodPosition_j(t-1)-X_j^i(t-1))\times rand\tag{1} Xji(t)=Xji(t−1)+(FoodPositionj(t−1)−Xji(t−1))×rand(1)其中, F o o d P o s i t i o n j ( t − 1 ) FoodPosition_j(t-1) FoodPositionj(t−1)与 X j i ( t − 1 ) X_j^i(t-1) Xji(t−1)分别是上轮迭代中食物源和第 i i i个领导者的第 j j j维位置, r a n d rand rand为 ( 0 , 1 ) (0,1) (0,1)之间均匀分布的随机数。通过引入上一代自身位置信息,樽海鞘领导者能够更好地继承已有的进化成果,增强全局搜索的有效性。
2.1.2 非线性惯性权重
本文还在领导者位置更新公式中增加了自适应惯性权重 w w w,权重值的大小控制着当前全局最优位置(食物源)对领导者位置更新的影响,从而决定了领导者的全局搜索能力。 w w w的值随着进化代数的递增呈非线性递减趋势,迭代前期 w w w比较大,领导者受食物源位置影响较强,从上代位置向较大空间范围广度搜索,而进化后期领导者已搜索至全局最优区域,此时较小的 w w w取值能使领导者在上轮进化到达的位置附近精细挖掘,增强了算法全局和局部搜索的平衡性,提高了寻优能力和求解精度。 w w w计算为: w = e 2 ( 1 − t / M a x _ i t e r ) − e − 2 ( 1 − t / M a x _ i t e r ) e 2 ( 1 − t / M a x _ i t e r ) + e − 2 ( 1 − t / M a x _ i t e r ) (2) w=\frac{e^{2(1-t/Max\_iter)}-e^{-2(1-t/Max\_iter)}}{e^{2(1-t/Max\_iter)}+e^{-2(1-t/Max\_iter)}}\tag{2} w=e2(1−t/Max_iter)+e−2(1−t/Max_iter)e2(1−t/Max_iter)−e−2(1−t/Max_iter)(2)加入 w w w的新的樽海鞘领导者位置更新公式为: X j i ( t ) = X j i ( t − 1 ) + ( w × F o o d P o s i t i o n j ( t − 1 ) − X j i ( t − 1 ) ) × r a n d (3) X_j^i(t)=X_j^i(t-1)+(w\times FoodPosition_j(t-1)-X_j^i(t-1))\times rand\tag{3} Xji(t)=Xji(t−1)+(w×FoodPositionj(t−1)−Xji(t−1))×rand(3)其中, w w w的取值随进化代数的不断增加以双曲正切函数的方式非线性减小,其值域为 ( 0 , 1 ) (0,1) (0,1)。自适应权重的使用,更好地平衡了算法在不同进化阶段对领导者搜索能力的不同需求,使它们更有效、更合理地发挥领导作用,增强算法寻得全局最优解的可能和能力。
2.2 寄生和宿主双种群
受寄生现象启发,本文提出一种拥有双种群及2套进化机制的改进算法结构,在算法演化过程中始终维持着宿主和寄生2个种群,每个种群的个体数量均为 N N N。两者的进化策略不同,独立演化,其中宿主群使用标准SSA的位置更新公式,而寄生群则使用2.1节改进后的领导者更新方式。每隔 一定进化代数 M M M,就发生一次寄生群从宿主群吸收营养的寄生行为,即寄生群用 P P P个适应度值最差的个体置换宿主群中前 P P P个适应度值最好的个体。 P P P是每次寄生行为的个体置换数,取值随进化代数的增加自适应减小: P = r o u n d ( ( ( M a x _ i t e r − t ) / M a x _ i t e r ) × N / 4 ) (4) P=round(((Max\_iter-t)/Max\_iter)\times N/4)\tag{4} P=round(((Max_iter−t)/Max_iter)×N/4)(4)其中, r o u n d ( ) round() round()是四舍五入函数,用来对置换个数取整。随着进化代数不断增加,寄生行为也在不断发生,宿主群中位置较优的个体(营养)不断被寄生群吸走,寄生群已经得到了较多营养,因此交换个数也在不断递减,直到进化终止,寄生行为也随之彻底结束。
为了保持宿主种群的个体质量和活跃性,每一次寄生行为后还要对宿主种群中 一定比例的 Q Q Q个较差樽海鞘进行随机淘汰,替换以搜索空间中产生的随机个体 Q Q Q: Q = r o u n d ( ( 0.5 + r a n d ( ) / 2 ) × N / 4 ) (5) Q=round((0.5+rand()/2)\times N/4)\tag{5} Q=round((0.5+rand()/2)×N/4)(5)宿主群进行优胜劣汰的步骤为:
for i = 1:Q
if rand() > 0.5
淘汰替换当前个体;
end if
end for
通过对宿主种群中最差的 Q Q Q个樽海鞘个体实行随机劣汰,有效提升了宿主群的个体质量和多样性,降低了算法陷入局部极值的可能性.同时这一策略也很好地契合了自然进化和优化搜索机制中的优胜劣汰思想,较好地解决了由于宿主群中高质量樽海鞘个体持续流失减少而导致种群活跃度较低、易陷入低效搜索的问题。
2.3 PDESSA算法伪代码
PDESSA算法伪代码如下所示:
算法1. PDESSA.
begin
设置算法中基本参数的初值;
计算寄生群和宿主群中樽海鞘个体的初始位置;
计算2个种群中个体的适应度值;
设置宿主群、寄生群的食物源位置;
while (t <= Max_iter)
由式(2)计算w;
for i = 1 to N
if (i <= N/2)
for j = 1 to D
由式(3)对寄生群中的领导者进行位置更新;
end for
else
由标准SSA对应公式对寄生群中的追随者进行位置更新;
end if
end for
for i = 1 to N
if (i <= N/2)
for j = 1 to D
由标准SSA对应公式对寄生群中的领导者进行位置更新;
end for
else
由标准SSA对应公式对寄生群中的追随者进行位置更新;
end if
end for
if mod(t, M) == 0
由式(4)执行寄生行为;
由式(5)计算优胜劣汰个体数Q;
对宿主群中Q个较差个体进行随机劣汰替换;
end if
for i = 1 to N
对2个种群更新后的樽海鞘个体进行边界处理;
计算宿主群、寄生群中个体的适应度值;
对宿主群、寄生群的食物源位置进行更新;
end for
t = t + 1;
end while
end
二、仿真实验与结果分析
将PDESSA与SSA、ISSA、LSSA、PSO和PPSO进行对比,以文献[1]中表1的10个测试函数(30维)为例,实验设置种群规模为30,最大迭代次数为1000,每种算法独立运算50次,结果显示如下:
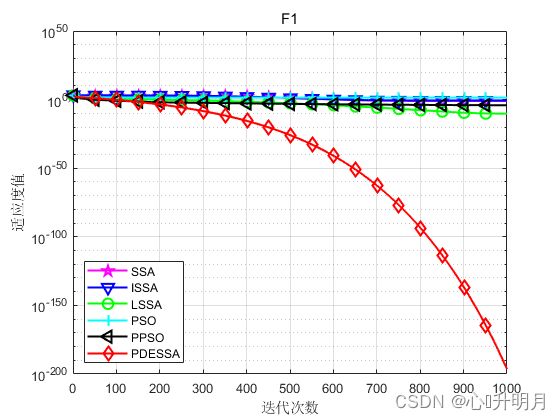





函数:F1
SSA:最差值: 0.60268, 最优值: 1.2726e-05, 平均值: 0.092831, 标准差: 0.13595, 秩和检验: 7.0661e-18
ISSA:最差值: 1.1463, 最优值: 0.00013726, 平均值: 0.2121, 标准差: 0.32354, 秩和检验: 7.0661e-18
LSSA:最差值: 8.2669e-10, 最优值: 1.2136e-13, 平均值: 5.6797e-11, 标准差: 1.9369e-10, 秩和检验: 7.0661e-18
PSO:最差值: 59.6171, 最优值: 8.394, 平均值: 25.0052, 标准差: 10.6554, 秩和检验: 7.0661e-18
PPSO:最差值: 0.00053863, 最优值: 3.1127e-08, 平均值: 7.0931e-05, 标准差: 0.00011179, 秩和检验: 7.0661e-18
PDESSA:最差值: 4.6887e-196, 最优值: 1.4357e-200, 平均值: 3.5498e-197, 标准差: 0, 秩和检验: 1
函数:F2
SSA:最差值: 324.6818, 最优值: 20.4556, 平均值: 115.8918, 标准差: 68.6019, 秩和检验: 7.0661e-18
ISSA:最差值: 608.4754, 最优值: 2.6801, 平均值: 100.9297, 标准差: 127.5419, 秩和检验: 7.0661e-18
LSSA:最差值: 208.256, 最优值: 1.4921, 平均值: 19.4926, 标准差: 31.4628, 秩和检验: 7.0661e-18
PSO:最差值: 3572.1395, 最优值: 581.1936, 平均值: 1516.3655, 标准差: 712.5024, 秩和检验: 7.0661e-18
PPSO:最差值: 0.068826, 最优值: 4.8972e-08, 平均值: 0.006159, 标准差: 0.010971, 秩和检验: 7.0661e-18
PDESSA:最差值: 3.8609e-186, 最优值: 7.5026e-191, 平均值: 1.7714e-187, 标准差: 0, 秩和检验: 1
函数:F3
SSA:最差值: 13.7758, 最优值: 1.4676, 平均值: 5.3756, 标准差: 3.2284, 秩和检验: 7.0661e-18
ISSA:最差值: 4.8003e-10, 最优值: 5.5907e-11, 平均值: 1.8264e-10, 标准差: 8.6039e-11, 秩和检验: 0.66657
LSSA:最差值: 4.6205, 最优值: 8.4984e-15, 平均值: 1.6412, 标准差: 1.3351, 秩和检验: 4.7329e-09
PSO:最差值: 51.7263, 最优值: 4.4907, 平均值: 21.5779, 标准差: 10.8637, 秩和检验: 7.0661e-18
PPSO:最差值: 0.10722, 最优值: 5.7179e-05, 平均值: 0.0071591, 标准差: 0.025282, 秩和检验: 3.7755e-10
PDESSA:最差值: 1.0969, 最优值: 5.1801e-11, 平均值: 0.086957, 标准差: 0.27634, 秩和检验: 1
函数:F4
SSA:最差值: 88.1794, 最优值: 6.0001, 平均值: 20.7885, 标准差: 14.353, 秩和检验: 7.0661e-18
ISSA:最差值: 177.29, 最优值: 0.11852, 平均值: 27.0585, 标准差: 36.2926, 秩和检验: 7.0661e-18
LSSA:最差值: 2.8289, 最优值: 0.27416, 平均值: 1.0629, 标准差: 0.62067, 秩和检验: 7.0661e-18
PSO:最差值: 253.6672, 最优值: 20.4783, 平均值: 107.1036, 标准差: 48.4161, 秩和检验: 7.0661e-18
PPSO:最差值: 0.010586, 最优值: 5.3936e-08, 平均值: 0.0015509, 标准差: 0.0027611, 秩和检验: 7.0661e-18
PDESSA:最差值: 1.4409e-193, 最优值: 1.6424e-198, 平均值: 5.3655e-195, 标准差: 0, 秩和检验: 1
函数:F5
SSA:最差值: 0.15829, 最优值: 0.011906, 平均值: 0.041502, 标准差: 0.025531, 秩和检验: 7.0661e-18
ISSA:最差值: 8.5586e-05, 最优值: 7.4264e-06, 平均值: 2.7425e-05, 标准差: 1.6641e-05, 秩和检验: 7.0661e-18
LSSA:最差值: 0.068499, 最优值: 0.0058053, 平均值: 0.022984, 标准差: 0.012208, 秩和检验: 7.0661e-18
PSO:最差值: 149.9085, 最优值: 27.1853, 平均值: 62.7852, 标准差: 26.521, 秩和检验: 7.0661e-18
PPSO:最差值: 0.085213, 最优值: 2.0839e-07, 平均值: 0.010217, 标准差: 0.017227, 秩和检验: 2.6246e-17
PDESSA:最差值: 1.3095e-06, 最优值: 8.5808e-176, 平均值: 2.2151e-07, 标准差: 3.3973e-07, 秩和检验: 1
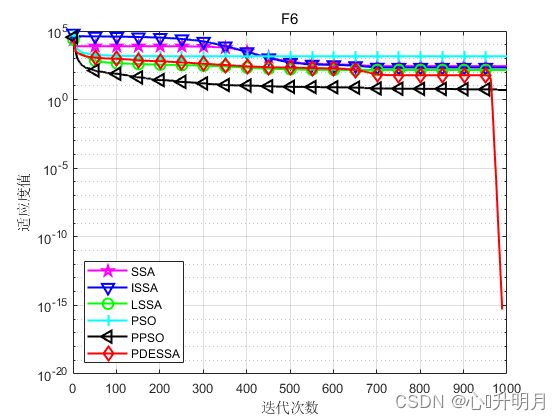
函数:F6
SSA:最差值: 469.5, 最优值: 130, 平均值: 272.935, 标准差: 72.1608, 秩和检验: 3.3111e-20
ISSA:最差值: 361, 最优值: 108, 平均值: 219.35, 标准差: 61.2571, 秩和检验: 3.3111e-20
LSSA:最差值: 264, 最优值: 67, 平均值: 144.54, 标准差: 41.8565, 秩和检验: 3.3111e-20
PSO:最差值: 2704.6159, 最优值: 714.0441, 平均值: 1431.2022, 标准差: 450.6295, 秩和检验: 3.3111e-20
PPSO:最差值: 28, 最优值: 6.6725e-07, 平均值: 4.9542, 标准差: 8.7431, 秩和检验: 3.3072e-20
PDESSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数:F7
SSA:最差值: 7.0639, 最优值: 0.55163, 平均值: 3.0154, 标准差: 1.5832, 秩和检验: 7.0661e-18
ISSA:最差值: 0.012784, 最优值: 7.9407e-05, 平均值: 0.0058373, 标准差: 0.0032472, 秩和检验: 7.0661e-18
LSSA:最差值: 0.17851, 最优值: 0.019504, 平均值: 0.078893, 标准差: 0.040369, 秩和检验: 7.0661e-18
PSO:最差值: 14.608, 最优值: 4.5104, 平均值: 8.7201, 标准差: 2.4649, 秩和检验: 7.0661e-18
PPSO:最差值: 0.011978, 最优值: 5.5611e-06, 平均值: 0.0032652, 标准差: 0.003017, 秩和检验: 7.0661e-18
PDESSA:最差值: 1.6537e-11, 最优值: 6.2387e-102, 平均值: 3.6707e-13, 标准差: 2.3439e-12, 秩和检验: 1
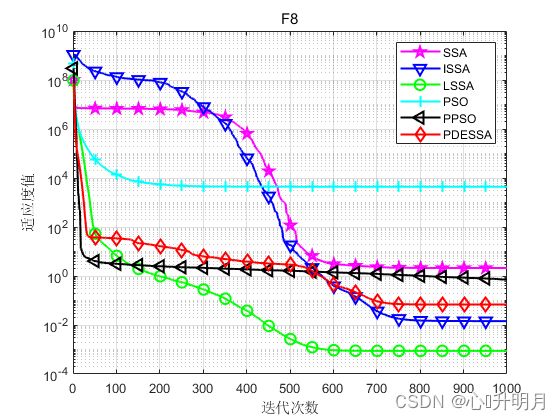
函数:F8
SSA:最差值: 37.9008, 最优值: 6.0149e-10, 平均值: 2.1145, 标准差: 7.3401, 秩和检验: 0.045214
ISSA:最差值: 0.39698, 最优值: 1.0417e-09, 平均值: 0.014456, 标准差: 0.055881, 秩和检验: 0.67662
LSSA:最差值: 0.010987, 最优值: 9.3426e-14, 平均值: 0.00087899, 标准差: 0.0030111, 秩和检验: 3.5664e-15
PSO:最差值: 24802.5549, 最优值: 46.2943, 平均值: 4399.042, 标准差: 6746.1883, 秩和检验: 7.0661e-18
PPSO:最差值: 1.8652, 最优值: 0.017415, 平均值: 0.71084, 标准差: 0.49893, 秩和检验: 3.195e-16
PDESSA:最差值: 2.9661, 最优值: 9.3873e-10, 平均值: 0.068447, 标准差: 0.4185, 秩和检验: 1
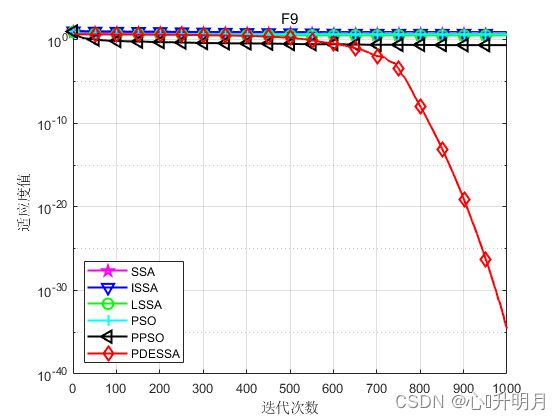
函数:F9
SSA:最差值: 5.4692, 最优值: 2.4961, 平均值: 4.2492, 标准差: 0.68287, 秩和检验: 7.0661e-18
ISSA:最差值: 8.398, 最优值: 2.8603, 平均值: 5.5199, 标准差: 1.1049, 秩和检验: 7.0661e-18
LSSA:最差值: 4.3045, 最优值: 1.2428, 平均值: 3.2471, 标准差: 0.68004, 秩和检验: 7.0661e-18
PSO:最差值: 5.9129, 最优值: 3.1269, 平均值: 4.5354, 标准差: 0.58251, 秩和检验: 7.0661e-18
PPSO:最差值: 0.87674, 最优值: 0.016714, 平均值: 0.21884, 标准差: 0.17187, 秩和检验: 7.0661e-18
PDESSA:最差值: 1.2098e-33, 最优值: 5.6897e-45, 平均值: 2.671e-35, 标准差: 1.7102e-34, 秩和检验: 1
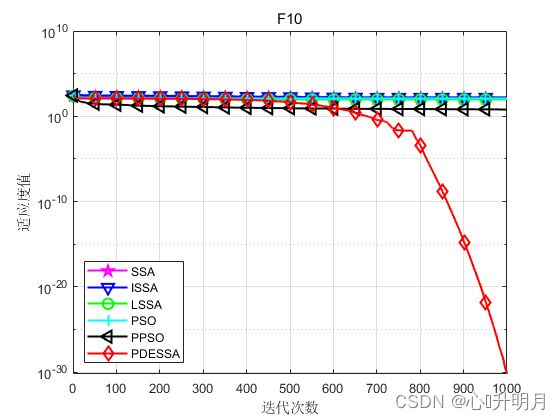
函数:F10
SSA:最差值: 143.797, 最优值: 88.3714, 平均值: 124.6833, 标准差: 12.4652, 秩和检验: 7.0661e-18
ISSA:最差值: 257.2422, 最优值: 94.5284, 平均值: 163.7889, 标准差: 38.3401, 秩和检验: 7.0661e-18
LSSA:最差值: 119.1917, 最优值: 61.2693, 平均值: 95.2833, 标准差: 14.3962, 秩和检验: 7.0661e-18
PSO:最差值: 153.9851, 最优值: 111.2559, 平均值: 128.049, 标准差: 10.6572, 秩和检验: 7.0661e-18
PPSO:最差值: 15.5735, 最优值: 0.89728, 平均值: 6.1389, 标准差: 3.1863, 秩和检验: 7.0661e-18
PDESSA:最差值: 3.0695e-29, 最优值: 6.1572e-44, 平均值: 6.1434e-31, 标准差: 4.3409e-30, 秩和检验: 1
实验结果表明:PDESSA算法的寻优精度、收敛性能均有显著提高和改善。
三、参考文献
[1] 刘景森, 袁蒙蒙, 李煜. 基于改进的樽海鞘群算法求解机器人路径规划问题[J]. 计算机研究与发展, 2022, 59(6): 1297-1314.