动手学习深度学习 05：深度学习计算

01 层和块

神经网络的核心组件是层(layer)(layer)，它是一种数据处理模块，我们可以将其看作数据过滤器。输入一些数据经过处理后，输出的数据变得更加有用。

事实证明，研究讨论“比单个层大”但“比整个模型小”的组件更有价值。 例如，在计算机视觉中广泛流行的ResNet-152架构就有数百层， 这些层是由层组（groups of layers）的重复模式组成。 这个ResNet架构赢得了2015年ImageNet和COCO计算机视觉比赛 的识别和检测任务 [He et al., 2016a]。 目前ResNet架构仍然是许多视觉任务的首选架构。 在其他的领域，如自然语言处理和语音， 层组以各种重复模式排列的类似架构现在也是普遍存在。

为了实现这些复杂的网络，我们引入了神经网络块的概念。 **块（block）**可以描述单个层、由多个层组成的组件或整个模型本身。

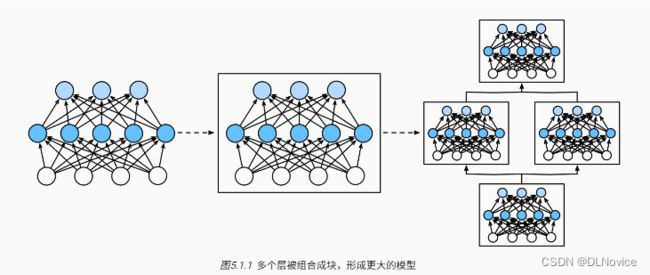
使用块进行抽象的一个好处是可以将一些块组合成更大的组件， 这一过程通常是递归的，如下所示。 通过定义代码来按需生成任意复杂度的块， 我们可以通过简洁的代码实现复杂的神经网络。

从编程的角度来看，块由类（class）表示。

• 它的任何子类都必须定义一个将其输入转换为输出的前向传播函数， 并且必须存储任何必需的参数。 注意，有些块不需要任何参数。
• 最后，为了计算梯度，块必须具有反向传播函数。
• 在定义我们自己的块时，由于自动微分提供了一些后端实现，我们只需要考虑前向传播函数和必需的参数。

构造自定义块之前，先回顾一下多层感知机 :

import torch
from torch import nn
from torch.nn import functional as F

MLP:

# 生成一个网络，其中包含一个具有256个单元和ReLU激活函数的全连接隐藏层， 然后是一个具有10个隐藏单元且不带激活函数的全连接输出层。
net = nn.Sequential(nn.Linear(20, 256), nn.ReLU(), nn.Linear(256, 10))

X = torch.rand(2, 20)
net(X)

结果展示：

tensor([[ 0.0990, -0.1185,  0.0419,  0.1634,  0.1016, -0.1388, -0.1298,  0.0226,
         -0.0349,  0.3598],
        [ 0.0337,  0.0127,  0.1110,  0.1346,  0.1686, -0.1331, -0.1283,  0.0392,
          0.0538,  0.3149]], grad_fn=<AddmmBackward0>)

在这个例子中，我们通过实例化nn.Sequential来构建我们的模型， 层的执行顺序是作为参数传递的。简而言之，nn.Sequential定义了一种特殊的Module， 即在PyTorch中表示一个块的类， 它维护了一个由Module组成的有序列表。这个前向传播函数非常简单： 它将列表中的每个块连接在一起，将每个块的输出作为下一个块的输入。

PS:

• 通过net(X)调用我们的模型来获得模型的输出。 这实际上是net.__call__(X)的简写。

1、自定义块

官网：[模块 — PyTorch 1.12 文档](https://pytorch.org/docs/stable/generated/torch.nn.Module.html?highlight=torch nn module#torch.nn.Module)

在实现我们自定义块之前，我们简要总结一下每个块必须提供的基本功能：

1. 将输入数据作为其前向传播函数的参数。
2. 通过前向传播函数来生成输出。请注意，输出的形状可能与输入的形状不同。例如，我们上面模型中的第一个全连接的层接收一个20维的输入，但是返回一个维度为256的输出。
3. 计算其输出关于输入的梯度，可通过其反向传播函数进行访问。通常这是自动发生的。
4. 存储和访问前向传播计算所需的参数。
5. 根据需要初始化模型参数。

下面开始从零编写一个块：

• 它包含一个多层感知机：具有256个隐藏单元的隐藏层和一个10维输出层。

注意，下面的MLP类继承了表示块的类。 我们的实现只需要提供我们自己的构造函数（Python中的__init__函数）和前向传播函数。

import torch
from torch import nn
from torch.nn import functional as F

class MLP(nn.Module):
    # 用模型参数声明层。这里，我们声明两个全连接的层
    def __init__(self):
        # 调用MLP的父类Module的构造函数来执行必要的初始化。
        # 这样，在类实例化时也可以指定其他函数参数，例如模型参数params（稍后将介绍）
        super().__init__()
        self.hidden = nn.Linear(20, 256)  # 隐藏层
        self.out = nn.Linear(256, 10)  # 输出层

    # 定义模型的前向传播，即如何根据输入X返回所需的模型输出
    def forward(self, X):
        # 注意，这里我们使用ReLU的函数版本，其在nn.functional模块中定义。
        return self.out(F.relu(self.hidden(X)))

解释一下上述代码：

• 首先看一下前向传播函数，它以X作为输入， 计算带有激活函数的隐藏表示，并输出其未规范化的输出值。
• 接着我们实例化多层感知机的层，然后在每次调用前向传播函数时调用这些层。
• 注意一些细节：
  • 首先，我们定制的__init__函数通过super().__init__() 调用父类的__init__函数， 省去了重复编写模版代码的痛苦。
  • 然后，我们实例化两个全连接层， 分别为self.hidden和self.out。
  • 注意，除非我们实现一个新的运算符， 否则我们不必担心反向传播函数或参数初始化， 系统将自动生成这些。

注意：Module是一个很重要的概念，任何一个层or神经网络都是Module的一个子类

我们通过继承nn.Module，得到了许多好用的函数

试试效果：

net = MLP()
X = torch.rand(2, 20)
net(X)

tensor([[-0.1730, -0.0511,  0.0732, -0.0387, -0.0652,  0.1398, -0.0518,  0.1300,
         -0.1930,  0.1469],
        [-0.0716,  0.0471,  0.0296,  0.0022, -0.0850,  0.0250,  0.1149,  0.1642,
         -0.2126,  0.2025]], grad_fn=<AddmmBackward0>)

块的一个主要优点是它的多功能性。 我们可以子类化块以创建层（如全连接层的类）、 整个模型（如上面的MLP类）或具有中等复杂度的各种组件。

2、顺序块

现在我们可以更仔细地看看Sequential类是如何工作的， 回想一下Sequential的设计是为了把其他模块串起来。 为了构建我们自己的简化的MySequential， 我们只需要定义两个关键函数：

1. 一种将块逐个追加到列表中的函数。
2. 一种前向传播函数，用于将输入按追加块的顺序传递给块组成的“链条”。

class MySequential(nn.Module):
    def __init__(self, *args):
        super().__init__()
        for idx, module in enumerate(args):
            # 这里，module是Module子类的一个实例。我们把它保存在'Module'类的成员
            # 变量_modules中。_module的类型是OrderedDict
            self._modules[str(idx)] = module

    def forward(self, X):
        # OrderedDict保证了按照成员添加的顺序遍历它们
        for block in self._modules.values():
            X = block(X)
        return X

__init__函数将每个模块逐个添加到有序字典_modules中。

• _modules的主要优点是： 在模块的参数初始化过程中， 系统知道在_modules字典中查找需要初始化参数的子块。

当MySequential的前向传播函数被调用时， 每个添加的块都按照它们被添加的顺序执行。

net = MySequential(nn.Linear(20, 256), nn.ReLU(), nn.Linear(256, 10))
net(X)

效果：

tensor([[ 9.3941e-03,  3.4989e-03,  8.4566e-02,  4.2083e-02, -1.6684e-01,
         -1.4397e-01,  7.5649e-02, -5.1131e-01, -8.8932e-02, -1.5541e-01],
        [-1.1243e-02, -4.2361e-04,  3.3980e-02,  7.8550e-02, -2.2633e-01,
         -1.0471e-02,  1.4429e-02, -2.2961e-01,  3.8093e-02, -1.0829e-01]],
       grad_fn=<AddmmBackward0>)

3、在前向传播函数中执行代码

Sequential类使模型构造变得简单， 允许我们组合新的架构，而不必定义自己的类。 然而，并不是所有的架构都是简单的顺序架构。 当需要更强的灵活性时，我们需要定义自己的块。

• 简单来说：当我们需要更灵活的计算时，可以在init、forward等处做大量自定义的计算

到目前为止， 我们网络中的所有操作都对网络的激活值及网络的参数起作用。 然而，有时我们可能希望合并既不是上一层的结果也不是可更新参数的项， 我们称之为常数参数（constant parameter）。

• 例如，我们需要一个计算函数 f(x,w)=c⋅w ⊤ x的层， 其中x是输入， w是参数， c是某个在优化过程中没有更新的指定常量。
• 因此我们实现了一个FixedHiddenMLP类，如下所示：

class FixedHiddenMLP(nn.Module):
    def __init__(self):
        super().__init__()
        # 不计算梯度的随机权重参数。因此其在训练期间保持不变
        self.rand_weight = torch.rand((20, 20), requires_grad=False)
        self.linear = nn.Linear(20, 20)

    def forward(self, X):
        X = self.linear(X)
        # 使用创建的常量参数以及relu和mm函数
        X = F.relu(torch.mm(X, self.rand_weight) + 1)
        # 复用全连接层。这相当于两个全连接层共享参数
        X = self.linear(X)
        # 控制流
        while X.abs().sum() > 1:
            X /= 2
        return X.sum()

在这个FixedHiddenMLP模型中，我们实现了一个隐藏层， 其权重（self.rand_weight）在实例化时被随机初始化，之后为常量。 这个权重不是一个模型参数，因此它永远不会被反向传播更新。 然后，神经网络将这个固定层的输出通过一个全连接层。

注意，这里i有个操作可能不会常用于在任何实际任务中：

• 在返回输出之前，模型运行了一个while循环，在L1范数大于1的条件下， 将输出向量除以2，直到它满足条件为止。
• 此操作可能不会常用于在任何实际任务中， 我们只是向你展示如何将任意代码集成到神经网络计算的流程中。

效果展示：

net = FixedHiddenMLP()
net(X)

tensor(-0.1451, grad_fn=<SumBackward0>)

我们可以混合搭配各种组合块的方法。

下面，我们尝试一下嵌套块：

class NestMLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(nn.Linear(20, 64), nn.ReLU(),
                                 nn.Linear(64, 32), nn.ReLU())
        self.linear = nn.Linear(32, 16)

    def forward(self, X):
        return self.linear(self.net(X))

chimera = nn.Sequential(NestMLP(), nn.Linear(16, 20), FixedHiddenMLP())
chimera(X)

tensor(-0.3847, grad_fn=<SumBackward0>)

4、效率

你可能会开始担心操作效率的问题。 毕竟，我们在一个高性能的深度学习库中进行了大量的字典查找、 代码执行和许多其他的Python代码。

Python的问题全局解释器锁 是众所周知的。 在深度学习环境中，我们担心速度极快的GPU可能要等到CPU运行Python代码后才能运行另一个作业。

5、小结

• 一个块可以由许多层组成；一个块可以由许多块组成。
• 块可以包含代码。
• 块负责大量的内部处理，包括参数初始化和反向传播。
• 层和块的顺序连接由Sequential块处理。

02 参数管理

之前的介绍中，我们只依靠深度学习框架来完成训练的工作， 而忽略了操作参数的具体细节。

主要内容：

• 访问参数，用于调试、诊断和可视化。
• 参数初始化。
• 在不同模型组件间共享参数

我们首先看一下具有单隐藏层的多层感知机。

import torch
from torch import nn

net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(), nn.Linear(8, 1))
X = torch.rand(size=(2, 4))
net(X)

tensor([[-0.6436],
        [-0.6306]], grad_fn=<AddmmBackward0>)

1、参数访问

当通过Sequential类定义模型时， 我们可以通过索引来访问模型的任意层。

如下，检查第二个全连接层的参数：

print(net[2].state_dict())

OrderedDict([('weight', tensor([[ 0.2729,  0.2311,  0.2586, -0.2441, -0.0196, -0.3096, -0.0893, -0.2219]])), ('bias', tensor([-0.2187]))])

输出显示：这个全连接层包含两个参数，分别是该层的权重和偏置。

1.1、目标参数

注意，每个参数都表示为参数类的一个实例。 要对参数执行任何操作，首先我们需要访问底层的数值。 有几种方法可以做到这一点。

如下：从第二个全连接层（即第三个神经网络层）提取偏置， 提取后返回的是一个参数类实例，并进一步访问该参数的值。

print(type(net[2].bias))
print(net[2].bias)
print(net[2].bias.data)

<class 'torch.nn.parameter.Parameter'>
Parameter containing:
tensor([-0.2187], requires_grad=True)
tensor([-0.2187])

参数是复合的对象，包含值、梯度和额外信息。 这就是我们需要显式参数值的原因。 除了值之外，我们还可以访问每个参数的梯度。

如下：

（由于我们还没有调用反向传播，所以参数的梯度处于初始状态。）

net[2].weight.grad == None  # True

1.2、一次性访问所有参数

当我们需要对所有参数执行操作时，逐个访问它们可能会很麻烦。

下面，我们通过代码演示访问第一个全连接层的参数和访问所有层。

print(*[(name, param.shape) for name, param in net[0].named_parameters()])
print(*[(name, param.shape) for name, param in net.named_parameters()])

('weight', torch.Size([8, 4])) ('bias', torch.Size([8]))
('0.weight', torch.Size([8, 4])) ('0.bias', torch.Size([8])) ('2.weight', torch.Size([1, 8])) ('2.bias', torch.Size([1]))

另一种访问网络参数的方式：

net.state_dict()['2.bias'].data

tensor([-0.2187])

1.3、从嵌套块收集参数

我们首先定义一个生成块的函数（可以说是“块工厂”），然后将这些块组合到更大的块中。

def block1():
    return nn.Sequential(nn.Linear(4, 8), nn.ReLU(),
                         nn.Linear(8, 4), nn.ReLU())

def block2():
    net = nn.Sequential()
    for i in range(4):
        # 在这里嵌套
        net.add_module(f'block {i}', block1())
    return net

rgnet = nn.Sequential(block2(), nn.Linear(4, 1))
rgnet(X)

tensor([[-0.1277],
        [-0.1277]], grad_fn=<AddmmBackward0>)

设计了网络后，我们看看它是如何工作的。

print(rgnet)

Sequential(
  (0): Sequential(
    (block 0): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
    (block 1): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
    (block 2): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
    (block 3): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
  )
  (1): Linear(in_features=4, out_features=1, bias=True)
)

因为层是分层嵌套的，所以我们也可以像通过嵌套列表索引一样访问它们。

# 访问第一个主要的块中、第二个子块的第一层的偏置项
rgnet[0][1][0].bias.data

tensor([ 0.1477, -0.4444,  0.0925,  0.1432, -0.3879, -0.2950, -0.0100,  0.2417])

2、参数初始化

深度学习框架提供默认随机初始化， 也允许我们创建自定义初始化方法， 满足我们通过其他规则实现初始化权重。

• PyTorch：默认情况下，PyTorch会根据一个范围均匀地初始化权重和偏置矩阵， 这个范围是根据输入和输出维度计算出的。 PyTorch的nn.init模块提供了多种预置初始化方法。
• TF：默认情况下，Keras会根据一个范围均匀地初始化权重矩阵， 这个范围是根据输入和输出维度计算出的。 偏置参数设置为0。 TensorFlow在根模块和keras.initializers模块中提供了各种初始化方法。

2.1、内置初始化

让我们首先调用内置的初始化器。

def init_normal(m):
    if type(m) == nn.Linear:
        # 将所有权重参数初始化为标准差为0.01的高斯随机变量， 且将偏置参数设置为0。
        nn.init.normal_(m.weight, mean=0, std=0.01)
        nn.init.zeros_(m.bias)
net.apply(init_normal)
net[0].weight.data[0], net[0].bias.data[0]

(tensor([-0.0047, -0.0034,  0.0134,  0.0015]), tensor(0.))

我们还可以将所有参数初始化为给定的常数，比如初始化为1。

def init_constant(m):
    if type(m) == nn.Linear:
        nn.init.constant_(m.weight, 1)
        nn.init.zeros_(m.bias)
net.apply(init_constant)
net[0].weight.data[0], net[0].bias.data[0]

(tensor([1., 1., 1., 1.]), tensor(0.))

我们还可以对某些块应用不同的初始化方法。

def init_xavier(m):
    if type(m) == nn.Linear:
        nn.init.xavier_uniform_(m.weight)
def init_42(m):
    if type(m) == nn.Linear:
        # 使用Xavier初始化方法初始化第一个神经网络层， 然后将第三个神经网络层初始化为常量值42。
        nn.init.constant_(m.weight, 42)

net[0].apply(init_xavier)
net[2].apply(init_42)
print(net[0].weight.data[0])
print(net[2].weight.data)

tensor([ 0.0287, -0.0350,  0.4166,  0.4050])
tensor([[42., 42., 42., 42., 42., 42., 42., 42.]])

2.2、自定义初始化

有时，深度学习框架没有提供我们需要的初始化方法。我们需要自定义初始化

同样，我们实现了一个my_init函数来应用到net。

def my_init(m):
    if type(m) == nn.Linear:
        print("Init", *[(name, param.shape)
                        for name, param in m.named_parameters()][0])
        nn.init.uniform_(m.weight, -10, 10)
        m.weight.data *= m.weight.data.abs() >= 5

net.apply(my_init)
net[0].weight[:2]

Init weight torch.Size([8, 4])
Init weight torch.Size([1, 8])
tensor([[ 6.5782,  5.6446, -0.0000, -6.3349],
        [ 0.0000,  0.0000, -7.8131, -7.9950]], grad_fn=<SliceBackward0>)

注意，我们始终可以直接设置参数。

net[0].weight.data[:] += 1
net[0].weight.data[0, 0] = 42
net[0].weight.data[0]

tensor([42.0000,  6.6446,  1.0000, -5.3349])

3、参数绑定

有时我们希望在多个层间共享参数： 我们可以定义一个稠密层，然后使用它的参数来设置另一个层的参数。

# 我们需要给共享层一个名称，以便可以引用它的参数
shared = nn.Linear(8, 8)
net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(),
                    shared, nn.ReLU(),
                    shared, nn.ReLU(),
                    nn.Linear(8, 1))
net(X)
# 检查参数是否相同
print(net[2].weight.data[0] == net[4].weight.data[0])
net[2].weight.data[0, 0] = 100
# 确保它们实际上是同一个对象，而不只是有相同的值
print(net[2].weight.data[0] == net[4].weight.data[0])

tensor([True, True, True, True, True, True, True, True])
tensor([True, True, True, True, True, True, True, True])

这个例子表明第三个和第五个神经网络层的参数是绑定的。 它们不仅值相等，而且由相同的张量表示。 因此，如果我们改变其中一个参数，另一个参数也会改变。

你可能会思考：当参数绑定时，梯度会发生什么情况？ 答案是由于模型参数包含梯度，因此在反向传播期间第二个隐藏层 （即第三个神经网络层）和第三个隐藏层（即第五个神经网络层）的梯度会加在一起。

4、小结

• 我们有几种方法可以访问、初始化和绑定模型参数。
• 我们可以使用自定义初始化方法。

03 延后初始化

到目前为止，我们忽略了建立网络时需要做的以下这些事情：

• 我们定义了网络架构，但没有指定输入维度。
• 我们添加层时没有指定前一层的输出维度。
• 我们在初始化参数时，甚至没有足够的信息来确定模型应该包含多少参数。

你可能会对我们的代码能运行感到惊讶。 毕竟，深度学习框架无法判断网络的输入维度是什么。 这里的诀窍是框架的延后初始化（defers initialization）， 即直到数据第一次通过模型传递时，框架才会动态地推断出每个层的大小。

在以后，当使用卷积神经网络时， 由于输入维度（即图像的分辨率）将影响每个后续层的维数， 有了该技术将更加方便。 现在我们在编写代码时无须知道维度是什么就可以设置参数， 这种能力可以大大简化定义和修改模型的任务。 接下来，我们将更深入地研究初始化机制。

1、实例化网络

首先，让我们实例化一个多层感知机。

import tensorflow as tf

net = tf.keras.models.Sequential([
    tf.keras.layers.Dense(256, activation=tf.nn.relu),
    tf.keras.layers.Dense(10),
])

此时，因为输入维数是未知的，所以网络不可能知道输入层权重的维数。 因此，框架尚未初始化任何参数，我们通过尝试访问以下参数进行确认。

[net.layers[i].get_weights() for i in range(len(net.layers))]

[[], []]

请注意，每个层对象都存在，但权重为空。 使用net.get_weights()将抛出一个错误，因为权重尚未初始化。

接下来让我们将数据通过网络，最终使框架初始化参数。

X = tf.random.uniform((2, 20))
net(X)
[w.shape for w in net.get_weights()]

[(20, 256), (256,), (256, 10), (10,)]

一旦我们知道输入维数是20，框架可以通过代入值20来识别第一层权重矩阵的形状。 识别出第一层的形状后，框架处理第二层，依此类推，直到所有形状都已知为止。 注意，在这种情况下，只有第一层需要延迟初始化，但是框架仍是按顺序初始化的。 等到知道了所有的参数形状，框架就可以初始化参数。

2、小结

• 延后初始化使框架能够自动推断参数形状，使修改模型架构变得容易，避免了一些常见的错误。
• 我们可以通过模型传递数据，使框架最终初始化参数。

04 自定义层

深度学习成功背后的一个因素是神经网络的灵活性： 我们可以用创造性的方式组合不同的层，从而设计出适用于各种任务的架构。

1、不带参数的层

首先，我们构造一个没有任何参数的自定义层。

下面的CenteredLayer类要从其输入中减去均值。 要构建它，我们只需继承基础层类并实现前向传播功能。

import torch
import torch.nn.functional as F
from torch import nn


class CenteredLayer(nn.Module):
    def __init__(self):
        super().__init__()

    def forward(self, X):
        return X - X.mean()

向该层提供一些数据，验证它是否能按预期工作。

layer = CenteredLayer()
layer(torch.FloatTensor([1, 2, 3, 4, 5]))

tensor([-2., -1.,  0.,  1.,  2.])

现在，我们可以将层作为组件合并到更复杂的模型中。

net = nn.Sequential(nn.Linear(8, 128), CenteredLayer())

作为额外的健全性检查，我们可以在向该网络发送随机数据后，检查均值是否为0。 由于我们处理的是浮点数，因为存储精度的原因，我们仍然可能会看到一个非常小的非零数。

Y = net(torch.rand(4, 8))
Y.mean()

tensor(-2.9686e-09, grad_fn=<MeanBackward0>)

2、带参数的层

以上我们知道了如何定义简单的层，下面我们继续定义具有参数的层， 这些参数可以通过训练进行调整。 我们可以使用内置函数来创建参数，这些函数提供一些基本的管理功能。 比如管理访问、初始化、共享、保存和加载模型参数。 这样做的好处之一是：我们不需要为每个自定义层编写自定义的序列化程序。

现在，让我们实现自定义版本的全连接层。 回想一下，该层需要两个参数，一个用于表示权重，另一个用于表示偏置项。 在此实现中，我们使用修正线性单元作为激活函数。 该层需要输入参数：in_units和units，分别表示输入数和输出数。

class MyLinear(nn.Module):
    def __init__(self, in_units, units):
        super().__init__()
        self.weight = nn.Parameter(torch.randn(in_units, units))
        self.bias = nn.Parameter(torch.randn(units,))
    def forward(self, X):
        linear = torch.matmul(X, self.weight.data) + self.bias.data
        return F.relu(linear)

接下来，我们实例化MyLinear类并访问其模型参数。

linear = MyLinear(5, 3)
linear.weight

Parameter containing:
tensor([[-1.4779, -0.6027, -0.2225],
        [ 1.1270, -0.6127, -0.2008],
        [-2.1864, -1.0548,  0.2558],
        [ 0.0225,  0.0553,  0.4876],
        [ 0.3558,  1.1427,  1.0245]], requires_grad=True)

我们可以使用自定义层直接执行前向传播计算。

linear(torch.rand(2, 5))

tensor([[0.0000, 0.0000, 0.2187],
        [0.0000, 0.0000, 0.0000]])

我们还可以使用自定义层构建模型，就像使用内置的全连接层一样使用自定义层。

net = nn.Sequential(MyLinear(64, 8), MyLinear(8, 1))
net(torch.rand(2, 64))

tensor([[ 7.4571],
        [12.7505]])

3、 小结

• 我们可以通过基本层类设计自定义层。这允许我们定义灵活的新层，其行为与深度学习框架中的任何现有层不同。
• 在自定义层定义完成后，我们就可以在任意环境和网络架构中调用该自定义层。
• 层可以有局部参数，这些参数可以通过内置函数创建。

05 读写文件

到目前为止，我们讨论了如何处理数据， 以及如何构建、训练和测试深度学习模型。 然而，有时我们希望保存训练的模型， 以备将来在各种环境中使用（比如在部署中进行预测）。 此外，当运行一个耗时较长的训练过程时， 最佳的做法是定期保存中间结果， 以确保在服务器电源被不小心断掉时，我们不会损失几天的计算结果。 因此，现在是时候学习如何加载和存储权重向量和整个模型了。

1. 加载和保存张量

对于单个张量，我们可以直接调用load和save函数分别读写它们。 这两个函数都要求我们提供一个名称，save要求将要保存的变量作为输入。

import torch
from torch import nn
from torch.nn import functional as F

x = torch.arange(4)
torch.save(x, 'x-file')

我们现在可以将存储在文件中的数据读回内存。

x2 = torch.load('x-file')
x2

tensor([0, 1, 2, 3])

我们可以存储一个张量列表，然后把它们读回内存。

y = torch.zeros(4)
torch.save([x, y],'x-files')
x2, y2 = torch.load('x-files')
(x2, y2)

(tensor([0, 1, 2, 3]), tensor([0., 0., 0., 0.]))

我们甚至可以写入或读取从字符串映射到张量的字典。 当我们要读取或写入模型中的所有权重时，这很方便。

mydict = {'x': x, 'y': y}
torch.save(mydict, 'mydict')
mydict2 = torch.load('mydict')
mydict2

{'x': tensor([0, 1, 2, 3]), 'y': tensor([0., 0., 0., 0.])}

2、 加载和保存模型参数

保存单个权重向量（或其他张量）确实有用， 但是如果我们想保存整个模型，并在以后加载它们， 单独保存每个向量则会变得很麻烦。 毕竟，我们可能有数百个参数散布在各处。 因此，深度学习框架提供了内置函数来保存和加载整个网络。 需要注意的一个重要细节是，这将保存模型的参数而不是保存整个模型。 例如，如果我们有一个3层多层感知机，我们需要单独指定架构。 因为模型本身可以包含任意代码，所以模型本身难以序列化。 因此，为了恢复模型，我们需要用代码生成架构， 然后从磁盘加载参数。 让我们从熟悉的多层感知机开始尝试一下。

class MLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.hidden = nn.Linear(20, 256)
        self.output = nn.Linear(256, 10)

    def forward(self, x):
        return self.output(F.relu(self.hidden(x)))

net = MLP()
X = torch.randn(size=(2, 20))
Y = net(X)

接下来，我们将模型的参数存储在一个叫做“mlp.params”的文件中。

torch.save(net.state_dict(), 'mlp.params')

为了恢复模型，我们实例化了原始多层感知机模型的一个备份。 这里我们不需要随机初始化模型参数，而是直接读取文件中存储的参数。

clone = MLP()
clone.load_state_dict(torch.load('mlp.params'))
clone.eval()

MLP(
  (hidden): Linear(in_features=20, out_features=256, bias=True)
  (output): Linear(in_features=256, out_features=10, bias=True)
)

由于两个实例具有相同的模型参数，在输入相同的X时， 两个实例的计算结果应该相同。 让我们来验证一下。

Y_clone = clone(X)
Y_clone == Y

tensor([[True, True, True, True, True, True, True, True, True, True],
        [True, True, True, True, True, True, True, True, True, True]])

3、 小结

• save和load函数可用于张量对象的文件读写。
• 我们可以通过参数字典保存和加载网络的全部参数。
• 保存架构必须在代码中完成，而不是在参数中完成。

06 GPU

5.6. GPU — 动手学深度学习 2.0.0-beta1 documentation (d2l.ai)

QA：

07 房价预测总结

18 预测房价竞赛总结【动手学深度学习v2】_哔哩哔哩_bilibili