Matlab——噪声的检测和处理实验

       本次实验首先由matlab中的randn()函数模拟噪声信号，模拟确定性信号s(t)的抽样信号，并根据有无信号到达的概率，计算两者出现的频数，在matlab软件中仿真出有信号到达和无信号到达的两种接受信号。在此基础上，根据似然比和bayes检测理论，对接受信号进行有无信号的检测，由1000次实验结果计算检测概率 、误警概率 、漏警概率 和Bayes风险。最后，依题目问题要求，改变实验的参数并研究由此引起的影响。

本实验为确定性信号离散取样下的检测问题，似然比检测准则表述如下：

判定有信号，否则无信号到达。此处为判决门限，此处使用似然比检测方法时假设有无信号到达概率相同，故门限取0.5；在bayes检测时由风险系数和有无信号的概率决定：

问题一：利用似然比检测方法，对信号是否到达进行检测，同时完成计算各个判别概率。

程序代码：%用似然比检测方法，对1000个信号进行检测

clear;

t=0:199;

t1=0:50;

t2=51:150;

t3=151:199;

s1=0.02*t1;

s2=-0.02*t2+2;

s3=0.02*t3-4;

s=[s1,s2,s3];        %信号s(t)的取样向量s

n=5*randn(1000,200);

      %利用randn()函数仿真出噪声信号，产生1000个大小为200的噪声序列

x=n;

ww=zeros(1000,1); %存放所检测的结果,1为检测到有信号，0为检测结果为无信号

for i=1:500

    x(i,1:end)=x(i,1:end)+s; %前500个有信号到达时所接受的信号，后500个为无信号模拟

end

for j=1:1000  

    temp=x(j,1:end);

    if sum(temp.*s)>25*log(1)+0.5*sum(s.^2) %这里取有无信号到达的概率相同，故门限为1

    ww (j)=1;

    end

end

sum(ww)                    % 一次模拟结果为504等

pd=sum(ww(1:500))/500        %检测概率0.7960

pf=sum(ww(501:1000))/500      %虚警概率 0.2120

pm=1-pd                       %漏警概率 0.2040

bayes=pf*0.5+pm*0.5            %bayes风险 0.2080

%用bayes检测方法，对1000个信号进行检测

%相比用似然比检测方法，用bayes判别只是修改了到达信号中有无信号的比例和判别门限，修改的代码部分为：

for k=1:600

x(k,1:end)=x(k,1:end)+s; %前600个有信号到达时所接受的信号，后400个为无信号

end

for jj=1:1000  

    temp=x(jj,1:end);

    if sum(temp.*s)>25*log(4/3)+0.5*sum(s.^2) %这里取判别门限为[P(H0)*C10] / [P(H1)*C01]=4/3

    ww(jj)=1;

    end

end

sum(ww)                     % 一次模拟结果为 512

pd=sum(ww(1:600))/600        %检测概率 0.7450

pf=sum(ww(601:1000))/400      %虚警概率 0.1625

pm=1-pd                     %漏警概率 0.2550

bayes=pf*0.4*2+pm*0.6        %bayes风险 0.2830

      

分析：两种方法基本判别思想相同，判别门限因风险系数的变化有差别，由此造成的检测概率、虚警概率等稍有不同。

问题四：改变判决的门限，观察检测方法的、、和Bayes风险的变化；

%仍取有无信号的概率分别为0.6，0.4 改变风险系数C10 C01分别为1和2 其余风险系数默认为0，计算得判别门限为1/3

%用bayes检测方法，对1000个信号进行检测 (只给出修改部分)

for j=1:1000  

    temp=x(j,1:end);

    if sum(temp.*s)>25*log(1/3)+0.5*sum(s.^2) %这里取判别门限为[P(H0)*C10] / [P(H1)*C01]=1/3

   ww(j)=1;

    else ww(j)=0;

    end

end

s11=-0.02*t1;

s21=0.02*t2-2;

s31=-0.02*t3+4;

h=[s11,s21,s31];     %信号s(t)的匹配滤波器h（图形见上）

x1=5*randn(1,200)+s; %有信号到达时的接受信号

x0=5*randn(1,200);   %无信号到达时的接受信号

w1=conv(h,x1);        %有信号到达时通过系统滤波器后的结果

w0=conv(h,x0);        %无信号到达时通过系统滤波器后的结果

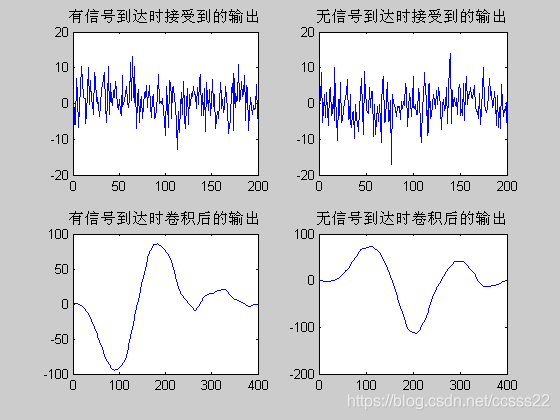
subplot(2,2,1);plot(x1);   %画图显示结果

title('有信号到达时接受到的输出');

subplot(2,2,3);plot(w1);

title('有信号到达时卷积后的输出');

subplot(2,2,2);plot(x0);

title('无信号到达时接受到的输出');

subplot(2,2,4);plot(w0);

title('无信号到达时卷积后的输出');

由下图可知，通过匹配器滤波后的波形可以比较清楚的判别有无信号到达。左下方的图形中，输出结果在t=200时达到最大值87，由此判别有信号到达；右下方的图形中，输出结果在t=200时达到-100，而判别门限经计算大约为37左右，据此可大致判别无信号到达。

       通过该实验，采用了似然比检测和bayes检测两种方法解决了确定性信号的检测问题，实验研究了判别门限、噪声方差和取样间隔等因素对信号判别的影响，并由检测概率、虚警概率、漏警概率和bayes风险等指标进行准确性的衡量，验证了与实际相符的结论。

D102