图像处理——Canny边缘检测及sobel介绍
Sobel算子介绍
在介绍sobel之前简单说明一下差分的概念。
差分:
与微分对应。差分对应于离散数据,微分对应于连续数据。差分的阶数与微分类
似,一次差分是一阶,差分后再差分就是二阶。
差分可以分为前向差分、后向差分和中心差分。
前向差分:
x k = x o + k h , ( k = 0 , 1 , . . . , n ) Δ f ( x k ) = f ( x k + 1 ) − f ( x k ) x_k=x_o+kh,(k=0,1,...,n)\\ \Delta f\left(x_{k}\right)=f\left(x_{k+1}\right)-f\left(x_{k}\right) xk=xo+kh,(k=0,1,...,n)Δf(xk)=f(xk+1)−f(xk)
后向差分:
Δ f ( x k ) = f ( x k ) − f ( x k − 1 ) \Delta f\left(x_{k}\right)=f\left(x_{k}\right)-f\left(x_{k-1}\right) Δf(xk)=f(xk)−f(xk−1)
中心差分:
Δ f ( x k ) = 1 2 ( f ( x k + 1 ) − f ( x k − 1 ) ) \Delta f\left(x_{k}\right)=\frac{1}{2}\left(f\left(x_{k+1}\right)-f\left(x_{k-1}\right)\right) Δf(xk)=21(f(xk+1)−f(xk−1))
差分的结果反映了离散量之间的一种变化,是研究离散数学的一种工具,常用函数差近似导数。
一阶导数的差分表示:
取 x = x k + 1 , x 0 = x k x=x_{k+1}, x_{0}=x_{k} x=xk+1,x0=xk,可得前向差分公式:
f ′ ( x k ) = f ( x k + 1 ) − f ( x k ) x k + 1 − x k f^{\prime}\left(x_{k}\right) = \frac{f\left(x_{k+1}\right)-f\left(x_{k}\right)}{x_{k+1}-x_{k}} f′(xk)=xk+1−xkf(xk+1)−f(xk)
取 x = x k − 1 , x 0 = x k x=x_{k-1}, x_{0}=x_{k} x=xk−1,x0=xk,可得后向差分公式:
f ′ ( x k ) = f ( x k ) − f ( x k − 1 ) x k − x k − 1 f^{\prime}\left(x_{k}\right) = \frac{f\left(x_{k}\right)-f\left(x_{k-1}\right)}{x_{k}-x_{k-1}} f′(xk)=xk−xk−1f(xk)−f(xk−1)
取 x 0 = x k x_0=x_k x0=xk, x x x分别取 x k − 1 , x k + 1 x_{k-1},x_{k+1} xk−1,xk+1并将两式相减,可得中心差分公式:
f ′ ( x k ) = f ( x k + 1 ) − f ( x k − 1 ) x k + 1 − x k − 1 f^{\prime}\left(x_{k}\right)=\frac{f\left(x_{k+1}\right)-f\left(x_{k-1}\right)}{x_{k+1}-x_{k-1}} f′(xk)=xk+1−xk−1f(xk+1)−f(xk−1)
二阶导数的差分表示
取 x 0 = x k , x x_0=x_k,x x0=xk,x分别取 x k − 1 , x k + 1 x_{k-1},x_{k+1} xk−1,xk+1并将两式相加,本质是对差分后的项再求差分,可得中心差分公式:
f ′ ′ ( x k ) = f ( x k + 1 ) + f ( x k − 1 ) − 2 f ( x k ) h 2 f^{\prime \prime}\left(x_{k}\right)=\frac{f\left(x_{k+1}\right)+f\left(x_{k-1}\right)-2 f\left(x_{k}\right)}{h^{2}} f′′(xk)=h2f(xk+1)+f(xk−1)−2f(xk)
Sobel 核
Soble 核的作用是充分提取像素附近 x 方向及 y 方向上的差分信息。
假设图像中某个像素 z 5 z_5 z5及其8邻域像素可表示为如图 :
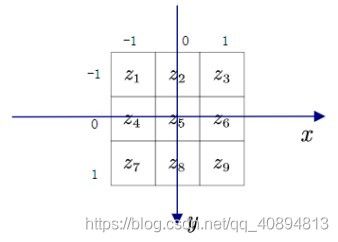
我们要从此邻域中提取四个方向的差分信息,即两个对角 ( z 1 , z 9 ) ( z 3 , z 7 ) (z_1,z_9)(z_3,z_7) (z1,z9)(z3,z7),一个垂直方向 ( z 2 , z 8 ) (z_2,z_8) (z2,z8),一个水平方向 ( z 6 , z 4 ) (z_6,z_4) (z6,z4)。给定四个向量来定义两两像素之间的差分方向,即 [ − 1 , 1 ] , [ 1 , 1 ] , [ 0 , 1 ] , [ 1 , 0 ] [-1,1],[1,1],[0,1],[1,0] [−1,1],[1,1],[0,1],[1,0],它们的具体取值与像素和 z 5 z_5 z5的位置相关,如上图所示,并且这四个向量与上述的四个像素对一一对应。
可以定义梯度矢量如下:
对于 ( z 3 , z 7 ) (z_3,z_7) (z3,z7),他们之间的距离参照曼哈顿距离,为2+2=4,则该像素对的梯度矢量为: ∣ g ( z 1 , z 9 ) ∣ = ( z 1 − z 9 ) [ − 1 , 1 ] 4 \left|g_{\left(z_{1}, z_{9}\right)}\right|=\frac{\left(z_{1}-z_{9}\right)[-1,1]}{4} ∣∣g(z1,z9)∣∣=4(z1−z9)[−1,1],以此类推,四个像素对的所构成的平均梯度矢量和为:
∣ g ∣ = ( ( z 1 − z 9 ) [ − 1 , 1 ] 4 + ( z 3 − z 7 ) [ 1 , 1 ] 4 + ( z 2 − z 8 ) [ 0 , 1 ] 2 + ( z 6 − z 4 ) [ 1 , 0 ] 2 ) 4 = ( [ − z 1 + z 9 + z 3 − z 7 + 2 z 6 − 2 z 4 , z 1 − z 9 + z 3 − z 7 + 2 z 2 − 2 z 8 ] ) 16 \begin{aligned} |g| &=\frac{\left(\frac{\left(z_{1}-z_{9}\right)[-1,1]}{4}+\frac{\left(z_{3}-z_{7}\right)[1,1]}{4}+\frac{\left(z_{2}-z_{8}\right)[0,1]}{2}+\frac{\left(z_{6}-z_{4}\right)[1,0]}{2}\right)}{4} \\ &=\frac{\left(\left[-z_{1}+z_{9}+z_{3}-z_{7}+2 z_{6}-2 z_{4}, z_{1}-z_{9}+z_{3}-z_{7}+2 z_{2}-2 z_{8}\right]\right)}{16} \end{aligned} ∣g∣=4(4(z1−z9)[−1,1]+4(z3−z7)[1,1]+2(z2−z8)[0,1]+2(z6−z4)[1,0])=16([−z1+z9+z3−z7+2z6−2z4,z1−z9+z3−z7+2z2−2z8])
考虑到整数运算速度更快、运算资源占用相对要小,所以,在求梯度矢量和时把分母去掉(相当于
原梯度矢量的值放大16倍),因为我们的最终目的是在图像中进行边缘检测,对所有的像素进行相同的操作对结果没有影响。那么就有:
∣ g ′ ∣ = [ − z 1 + z 9 + z 3 − z 7 + 2 z 6 − 2 z 4 , z 1 − z 9 + z 3 − z 7 + 2 z 2 − 2 z 8 ] = [ − z 1 + z 3 − 2 z 4 + 2 z 6 − z 7 + z 9 , z 1 + 2 z 2 + z 3 − z 7 − 2 z 8 − z 9 ] \begin{aligned} \left|g^{\prime}\right| &=\left[-z_{1}+z_{9}+z_{3}-z_{7}+2 z_{6}-2 z_{4}, z_{1}-z_{9}+z_{3}-z_{7}+2 z_{2}-2 z_{8}\right] \\ &=\left[-z_{1}+z_{3}-2 z_{4}+2 z_{6}-z_{7}+z_{9}, z_{1}+2 z_{2}+z_{3}-z_{7}-2 z_{8}-z_{9}\right] \end{aligned} ∣g′∣=[−z1+z9+z3−z7+2z6−2z4,z1−z9+z3−z7+2z2−2z8]=[−z1+z3−2z4+2z6−z7+z9,z1+2z2+z3−z7−2z8−z9]
可以在此公式中拆分出 x , y x,y x,y方向的梯度,则有:
∣ g ′ ∣ x = − z 1 + z 3 − 2 z 4 + 2 z 6 − z 7 + z 9 ∣ g ′ ∣ y = z 1 + 2 z 2 + z 3 − z 7 − 2 z 8 − z 9 \begin{aligned} \left|g^{\prime}\right|_{x}&=-z_{1}+z_{3}-2 z_{4}+2 z_{6}-z_{7}+z_{9} \\ \left|g^{\prime}\right|_{y}&=z_{1}+2 z_{2}+z_{3}-z_{7}-2 z_{8}-z_{9} \end{aligned} ∣g′∣x∣g′∣y=−z1+z3−2z4+2z6−z7+z9=z1+2z2+z3−z7−2z8−z9
将 ∣ g ′ ∣ x \left|g^{\prime}\right|_{x} ∣g′∣x转换为矩阵的形式以方便做卷积运算,则有:
G x = [ − 1 0 1 − 2 0 2 − 1 0 1 ] G_{x}=\left[\begin{array}{lll} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{array}\right] Gx=⎣⎡−1−2−1000121⎦⎤
同理, ∣ g ′ ∣ y \left|g^{\prime}\right|_{y} ∣g′∣y转换为:
G y = [ 1 2 1 0 0 0 − 1 − 2 − 1 ] G_{y}=\left[\begin{array}{ccc} 1 & 2 & 1 \\ 0 & 0 & 0 \\ -1 & -2 & -1 \end{array}\right] Gy=⎣⎡10−120−210−1⎦⎤
由此可推导出 G x , G y G_{x},G_{y} Gx,Gy为Sobel滤波器水平方向、垂直方向的算子。 G x , G y G_{x},G_{y} Gx,Gy并不唯一,通过改变差分顺序,可以形成不同的算子。
综上所述,Sobel算子所求得的并不是传统意义上的梯度,而是包含了四个方向像素差分的信息,相比较于只考虑一个方向的差分滤波器,它的边缘检测效果更佳。
Canny边缘检测
Canny 边缘检测是一种非常流行的边缘检测算法,是 John Canny 在 1986 年提出
的。它是一个多阶段的算法,即由多个步骤构成。
1. 图像降噪
我们知道梯度算子可以用于增强图像,本质上是通过增强边缘轮廓来实现的,也就是说是可以检测到边缘的。但是,它们受噪声的影响都很大。那么,我们第一步就是想到要先去除噪声,因为噪声就是灰度变化很大的地方,所以容易被识别为伪边缘。使用各种降噪算法把图片中的噪声处理掉(一般使用高斯核,进行低通滤波)。
2.计算图像梯度
使用 sobel 核卷积,计算图像梯度(通过四个方向的差分得到,并不是严格意义上的梯度),得到可能边缘。计算图像梯度能够得到图像的边缘,因为梯度是灰度变化明显的地方,而边缘也是灰度变化明显的地方。当然这一步只能得到可能的边缘。因为灰度变化的地方可能是边缘,也可能不是边缘。这一步就有了所有可能是边缘的集合。如下所示,通过sobel算子差分求得梯度及其方向。
Edge_Gradient ( G ) = G x 2 + G y 2 Angle ( θ ) = tan − 1 ( G y G x ) \begin{array}{c} \text { Edge\_Gradient }(G)=\sqrt{G_{x}^{2}+G_{y}^{2}} \\ \text { Angle }(\theta)=\tan ^{-1}\left(\frac{G_{y}}{G_{x}}\right) \end{array} Edge_Gradient (G)=Gx2+Gy2 Angle (θ)=tan−1(GxGy)
3.非极大值抑制
第三步,非极大值抑制。通常灰度变化的地方都比较集中,将局部范围内的梯度方向上,灰度变化最大的保留下来,其它的不保留,这样可以剔除掉一大部分的点。将有多个像素宽的边缘变成一个单像素宽的边缘。即“胖边缘”变成“瘦边缘”。具体如图所示
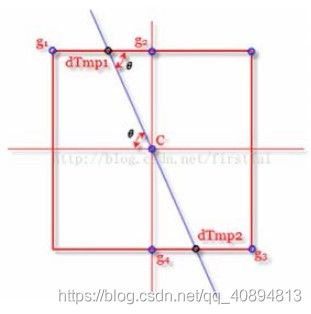
g 1 , g 2 , g 3 , g 4 , C g_{1}, g_{2}, g_{3}, g_{4}, C g1,g2,g3,g4,C都为像素点,在 g 1 , g 2 , g 3 , g 4 g_{1}, g_{2}, g_{3}, g_{4} g1,g2,g3,g4点上进行线性插值,并判断交点 d T m p 1 dTmp_1 dTmp1, d T m p 2 dTmp_2 dTmp2与 C C C的大小关系,从而判断 C C C是否为极大值, 若为极大值留下,否则取 0。这么做可以让边缘的线变细。
4.双阈值筛选
通过非极大值抑制后,仍然有很多的假的边缘点,进一步的设置一个双阈值,即低阈值,高阈值。灰度变化大于高阈值的,设置为强边缘像素,低于低阈值的,剔除。在低阈值和高阈值之间的设置为弱边缘。进一步判断,如果其领域内有强边缘像素,保留,如果没有,剔除。

这样做的目的是只保留强边缘轮廓的话,有些边缘可能不闭合,需要从满足低阈值和高阈值之间的点进行补充,使得边缘尽可能的闭合。还有一种方法是对于弱边缘像素,逐次判断该像素邻域上的点周围是否有强边缘点,有的话保存,没有剔除,迭代到没有没有弱边缘点为止。
Reference
https://www.zhihu.com/question/30416914
https://baike.baidu.com/item/%E5%B7%AE%E5%88%86/10349967?fr=aladdin
https://www.zhihu.com/question/266037140
https://blog.csdn.net/saltriver/article/details/80545571