深度学习学习笔记——线性代数矩阵的乘法运算

关于矩阵的运算,慢慢更新：

1.关于矩阵的乘法运算

总结一下矩阵的物理意义

矩阵和矩阵相乘的运算的定义：
设A是一个$m\times n$矩阵，B是一个$n\times s$ 矩阵，规定矩阵A和矩阵B的乘积是一个$m\times s$矩阵C

2.利用numpy实验

a=np.array(((1,2),(3,4)))
b=np.array([[5,6],[7,8]])
c=a+b
d=np.dot(a,b)
print("矩阵相乘d：")
print(d)

看代码
定义了一个2x2矩阵a
定义了一个2x2矩阵b
定义了一个矩阵d
d等于a和b两个矩阵相乘
d应该是一个2x2矩阵
d的结果可以算出来为

输出d

看看运行后的结果可以计算出的一样。

对于二维数组来说，调用shape（）方法哪个是“行”，哪个是“列”？

a=np.array(((1,2),(3,4)))
b=np.array([[5,6],[7,8]])
c=a+b
d=np.dot(a,b)
print("矩阵相乘d：")
print(d)
print("shape[0]=",d.shape[0])
print("shape[1]=",d.shape[1])

看代码，我们知道，对于d来说是一个2x2的矩阵，那么d.shape[0]=2,d.shape[1]=2,还是区分不了那个是行那个是列。
运行后的结果：

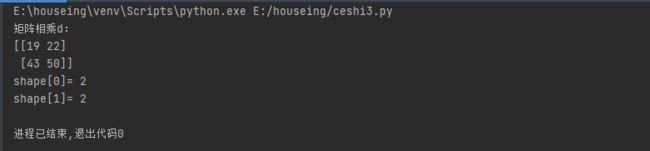
那么就让b为2x1的矩阵

a=np.array(((1,2),(3,4)))
b=np.array([[5],[7]])
c=a+b
d=np.dot(a,b)
print("矩阵相乘d：")
print(d)
print("shape[0]=",d.shape[0])
print("shape[1]=",d.shape[1])

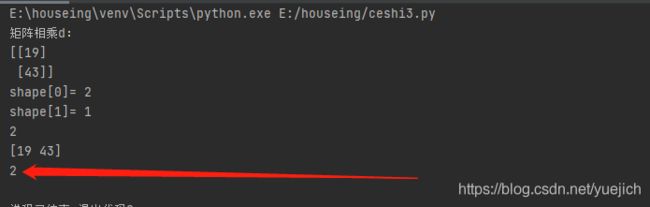
看代码，应该是下图的结果：

运行后代码为：

总结：shape[0]是行
shape[1]是列
但是对于一维的数组来说没有shape[1]

a=np.array(((1,2),(3,4)))
b=np.array([[5],[7]])
c=a+b
d=np.dot(a,b)
print("矩阵相乘d：")
print(d)
print("shape[0]=",d.shape[0])
print("shape[1]=",d.shape[1])
print(len(d))
d=np.squeeze(d)
print(d)
print(d.shape[0])
print(d.shape[1])#shape[1]会报错

运行后的结果：

下面去掉shape[1]

a=np.array(((1,2),(3,4)))
b=np.array([[5],[7]])
c=a+b
d=np.dot(a,b)
print("矩阵相乘d：")
print(d)
print("shape[0]=",d.shape[0])
print("shape[1]=",d.shape[1])
print(len(d))
d=np.squeeze(d)
print(d)
print(d.shape[0])

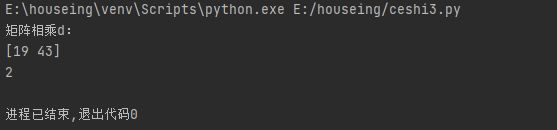
这里的2是行还是列，这个时候的b对应线性代数里面的是行向量还是列向量

继续实验；
看代码：让b为一个一维数组，他会默认为是2行1列，而不是1行2列

a=np.array(((1,2),(3,4)))

b=np.array([5,7])

d=np.dot(a,b)
print("矩阵相乘d：")
print(d)

运行结果

axb改为bxa看看结果：

a=np.array(((1,2),(3,4)))

b=np.array([5,7])

d=np.dot(b,a)#改变一下a和b的顺序
print("矩阵相乘d：")
print(d)
print(len(d))

让a转置试一下：

a=np.array(((1,2),(3,4)))

b=np.array([5,7])

d=np.dot(b,a.T)#改变一下a和b的顺序
print("矩阵相乘d：")
print(d)
print(len(d))

b转置实验一下：

a=np.array(((1,2),(3,4)))

b=np.array([5,7])

d=np.dot(b.T,a)#改变一下a和b的顺序
print("矩阵相乘d：")
print(d)
print(len(d))

总结：转置T对于一维向量没有作用，对于二维向量有作用。对于1维数组都是有几个数字，不分行和列

3.numpy怎么表示线性代数的行向量和列向量

a=np.array([[1,2]])#表示行向量，1行2列
b=np.array([[5],[7]])#表示列向量，2行1列
print("a为：",a)
print("a的类型：",type(a))
print("a的行数：",a.shape[0])
print("a的列数：",a.shape[1])
print("b为：",b)
print("b的类型为：",type(b))
print("b的行数：",b.shape[0])
print("b的列数：",b.shape[1])

看代码
a定义为一个行向量，1行4列
b定义为一个列向量，2行1列
运行一下实验结果是：

那么，$a\times b$是不是可以相乘呢，a为1行2列，b为2行1列，那么相乘就会得出一个1行1列的数19
看一下试试：

a=np.array([[1,2]])#表示行向量，1行2列
b=np.array([[5],[7]])#表示列向量，2行1列
print("a为：",a)
print("a的类型：",type(a))
print("a的行数：",a.shape[0])
print("a的列数：",a.shape[1])
print("b为：",b)
print("b的类型为：",type(b))
print("b的行数：",b.shape[0])
print("b的列数：",b.shape[1])
c=np.dot(a,b)
print("c为：")
print(c)
print("c的行",c.shape[0])
print("c的列：",c.shape[1])

运行后的结果：

1行1列