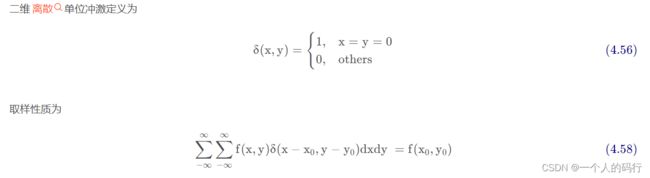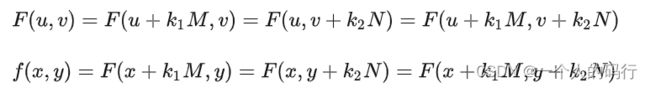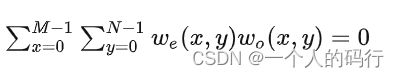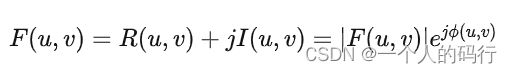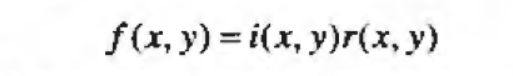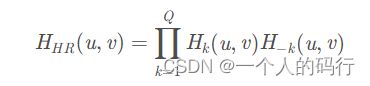图像增强技术总结
图像增强技术总结
文章目录
- 图像增强技术总结
-
- 1.数字图像基础
-
- 1.1人眼的图像感知
-
- 1.1.1人眼的结构
- 1.1.2亮度适应与辨别
- 1.2光和电磁波谱
- 1.3图像感知与获取
-
- 1.3.1使用单个传感器获取图像
- 1.3.2使用条带传感器获取图像
- 1.3.3使用阵列传感器获取图像
- 1.4图像取样和量化
- 1.5图像内插
-
- 1.5.1最近邻内插
- 1.5.2双线性内插
- 1.5.3双三次内插
- 1.6像素间的一些基本关系
-
- 1.6.1像素的相邻像素
- 1.6.2还有一些邻接,连通,区域和边界的概念。
- 1.7数字图像处理的基本工具
-
- 1.7.1空间运算
- 1.7.2向量和矩阵运算
- 1.7.3图像变换
- 2.灰度变换
-
- 2.1一些基本的灰度变换函数
-
- 2.1.1图像反转
- 2.1.2对数变换
- 2.1.3幂律变换
- 2.2分段线性变换函数
- 2.3直方图处理
-
- 2.3.1直方图均衡化
- 2.3.2直方图匹配
- 3.空间滤波
-
- 3.1空间相关与卷积
-
- 3.1.1可分离滤波器核
- 3.2平滑滤波器
-
- 3.2.1盒式滤波器核
- 3.2.2低通高斯滤波器核
- 3.2.3统计排序(非线性)滤波器
- 3.2.4锐化(高通)空间滤波器
-
- 3.2.4.1基础
- 3.2.4.2二阶导数锐化图像——拉普拉斯
- 3.2.4.3一阶导数锐化图像——梯度
- 梯度[算子](https://so.csdn.net/so/search?q=算子&spm=1001.2101.3001.7020)
- 3.2.5低通、高通、带阻、和带通滤波器
- 4.频率域滤波
-
- 4.1傅里叶变换基础
- 4.2单变量的离散傅里叶变换
- 4.3二变量函数的傅里叶变换
- 4.4二维DFT和IDFT的一些性质
- 4.5低通频率域滤波器平滑图像
-
- 4.5.1理想[低通滤波器](https://so.csdn.net/so/search?q=低通滤波器&spm=1001.2101.3001.7020)(ILPF)
- 4.5.2巴特沃斯低通滤波器
- 4.5.3高斯低通滤波器(GLPF)
- 4.6高通滤波器锐化图像
-
- 1.理想高通滤波器
- 2.巴特沃斯 (Butterworth)高通滤波器
- 3.高斯高通滤波器
- 4.频率域中的拉普拉斯算子
- 5.同态滤波
- 4.7快速傅里叶变换(FFT)
- 4.8选择性滤波
-
- 带阻滤波器和带通滤波器
- 陷波滤波器
- OK,到此总结基本完成。
1.数字图像基础
1.1人眼的图像感知
1.1.1人眼的结构
人眼的形状近似为一个球体,(直径约20mm),由三层膜包裹:外覆的角膜与巩膜、脉络膜、视网膜。
眼睛最靠内部的膜是视网膜,物体的光在视网膜上成像,模式视觉由分布在视网膜表面的各个分立光感受器提供。
1.1.2亮度适应与辨别
数字图像是作为离散灰度集来显示的。人类能适应的光强度范围很宽,从暗阈值到强闪光大约有10的10次方级。马赫带,同时对比,光学错视等都是人类视觉的感知现象。
1.2光和电磁波谱
频率和波长的关系公式:波长=光速*(1/频率)。
没有颜色的光称为单色光或无色光,描述彩色光源的量还有辐射光通量和亮度
| 发光强度I | 两种单位:烛光(c),坎德拉(cd) | 1c=1cd | |
|---|---|---|---|
| 光通量 | 每秒钟内光流量的度量 | 单位:流明(lm) | |
| 照度E | 入射到某表面的光通量称为该表面的照度 | 单位:lx,phot | |
| 反射 | 反射系数=表面反射的流明数/入射到该表面的流明数 | ||
| 透射 | 透射系数=物质透射的流明数/入射到该物质的流明数 | ||
| 亮度 | 主要有A,B两组单位衡量 | A组:cd作为单位,以每单位面积上的发光强度来表示 | B组:lm作为单位以每单位面积上发出的光通量来表示 |
1.3图像感知与获取
1.3.1使用单个传感器获取图像
最熟悉的是光二极管。传感器和成像区域之间必须有x方向和y方向的相对位移。缺点:速度慢,不便携带。
1.3.2使用条带传感器获取图像
医学和工业成像使用环形条带传感器获取三维物体的剖面图像。
1.3.3使用阵列传感器获取图像
1.4图像取样和量化
对坐标值进行数字化称为采样(或取样),对幅度值进行数字化称为量化。
数字图像的坐标约定是右手笛卡尔系。
动态范围:灰度跨越的值域
对比度:一幅图像中最高和最低灰度级间的灰度差
反差比:最高灰度级和最低灰度级的比率
坐标索引:一个像素的位置由其二维坐标给出的约定。
空间分辨率是图像中最小可辨别细节的测度。
灰度分辨率通常指量化灰度时所用的比特数。
1.5图像内插
1.5.1最近邻内插
假设一幅大小为500×500像素的图像要放大到750×750像素。一种简单的放大方法是创建一个假想的750×750网格,它与原始图像有相同的间隔。然后将其收缩,使它准确地与原图像匹配。显然收缩后的750×750网格的像素间隔要小于原图像的像素间隔。为了对覆盖的每一个点赋以灰度值,我们在原图像中寻找最接近的像素,并把该像素的灰度赋给750×750网格中的新像素。当我们完成对网格中覆盖的所有点的灰度赋值之后,就把图像扩展到原来规定的大小,得到放大后的图像。
1.5.2双线性内插
双线性内插法是使用邻近4 个点的像元值,按照其距内插点的距离赋予不同的权重,进行线性内插。
该方法具有平均化的低通滤波效果,边缘受到平滑作用,而产生一个比较连贯的输出图像。
缺点是破坏了原来的像元值,在后来的波谱识别分类分析中,会引起一些问题。
1.5.3双三次内插
1.6像素间的一些基本关系
1.6.1像素的相邻像素
邻域:坐标(x,y)处的像素p有2个水平的相邻像素,和2个垂直的相邻像素,这组像素称为p的4邻域。
加上四个对角的相邻像素则变成8邻域。
若包含p则称为闭域,不包含则称为开域。
1.6.2还有一些邻接,连通,区域和边界的概念。
1.7数字图像处理的基本工具
首先是矩阵运算,线性运算和非线性运算,
常用的有图像相加降低噪声,图像相减比较图像,图像相乘或相除校正阴影和模板
1.7.1空间运算
-
单像素运算
-
邻域运算
-
几何空间运算
包含了仿射变换,图像旋转,灰度内插,图像配准
1.7.2向量和矩阵运算
彩色图像比如rgb图像在每个像素都有三个分量,他们可以组织成一个列向量。
1.7.3图像变换
有些情况最好按照如下步骤:变换输入图像,在变换域执行规定的任务,执行反变换,返回空间域。
有一些变换是傅里叶变换,
2.灰度变换
2.1一些基本的灰度变换函数
2.1.1图像反转
使用一些基本的变换函数,得到灰度级在区间【0,L-1】内的反转图像。
2.1.2对数变换
![]()
对数变换将输入中范围较窄的低灰度值映射为输出中范围较宽的灰度值,或将输入中范围较宽的高灰度值映射为输出中范围较窄的灰度值。
对于对数函数,可以看到输入中范围在[0L/4]的灰度值映射为输出中范围为[03L/4]的灰度值,同理反对数函数也是这样理解。使用对数变换来扩展图像中的暗像素值,同时压缩更高灰度级的值。反对数函数的作用于此相反。
对数变换的通用形式为:
![]()
傅里叶频谱的图片进行对数变换
% 读取图像
img_1 = imread('Fig0305(a)(DFT_no_log).tif');
% 输入图像是uint8类型的,所以第一步先将输入图像转换成double型的:double(img_1)
% 对转换成double型的img_1,参照对数变换的公式,其中c = 1,调用log函数:log(1 + double(img_1))
% 将结果标定为[0, 1]范围内的double类的数组:mat2gray(log(1 + double(img_1)))
% 最后再将数组转换成uint8类型的图像:im2uint8(mat2gray(log(1 + double(img_1))))
img_2 = im2uint8(mat2gray(log(1 + double(img_1))));
% 显示图像
subplot(121), imshow(img_1);
subplot(122), imshow(img_2);
2.1.3幂律变换
图像伽马变化的基本形式为:
s=cr^y
![]()
伽马变换可以很好地拉伸图像的对比度,扩展灰度级。由图可知,当图像的整体灰度偏暗时,选择y<1,可以使图像增亮;当图像整体灰度偏亮时,选择y>1,可以使图像变暗,提高图像的对比度,凸显细节。
2.2分段线性变换函数
1.对比度拉伸
2.灰度级分层
3.比特平面分层
2.3直方图处理
灰度级(intensity levels)范围为[0,L-1]的数字图像的直方图可以用一个离散函数(discrete function)h(rk)=nk表示(此两处中的k原文是下标k,为了书写简便,没有用下标形式,特此说明,下同),其中rk是第k级灰度值,nk是图像中灰度为rk的像素个数。
假设M和N是图像的行数和列数,乘积MN表示的图像像素的总数,在实践中,常用每个灰度级的像素个数除以MN来归一化直方图(normalized histogram)。因此,归一化后的直方图由p(rk)=nk/MN给出,其中k=0、1、…、L-1,归一化直方图的所有分量之和应等于1。简单地说,p(rk)是灰度级在图像中出现的概率的一个估计。
直方图是多种空间域(spatial domain)处理技术的基础。直方图操作(Histogram manipulation)可用于提供有用的图像统计(image statistics)信息、图像增强(image enhancement)、图像压缩与分割。
直方图在软件中计算简单,而且有助于商用硬件实现,因已成为实时图像处理的一种流行工具。
2.3.1直方图均衡化
“直方图均衡化”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在更广泛灰度范围内的分布。直方图均衡化就是对图像进行非线性拉伸,重新分配图像像素值,使一定灰度范围内的像素数量大致相同。
这种方法提高图像整体的对比度,特别是有用数据的像素值分布比较接近时,在X光图像中使用广泛,可以提高骨架结构的显示,另外在曝光过度或不足的图像中可以更好的突出细节。
例图:
2.3.2直方图匹配
直方图匹配中的灰度变换不是根据图像本身的像素累积函数进行处理的,而是根据参照图片的像素累积分布函数,进行转换。
直方图规定化的原理:对两个直方图都做均衡化,变成相同的归一化的均匀直方图,以此均匀直方图为媒介,再对参考图像做均衡化的逆运算
意义: 直方图均衡化的优点能自动增强整个图像的对比度,但它的具体增强效果不易控制,处理的结果总是得到全局的均衡化的直方图。
实际工作中,有时需要变换直方图使之成为某个特定的形状,从而有选择地增强某个灰度值范围内的对比度,这时可采用比较灵活的直方图规定化(也成为直方图匹配)方法。
3.空间滤波
空间滤波器由
(1)一个邻域(典型地是一个较小的矩形);
(2)对该邻域包围的图像像素执行的预定义操作(predefined operation)组成。
滤波产生一个新像素,新像素的坐标等于邻域中心的坐标(coordinates of the center of the neighborhood),像索的值是滤波操作(operation filtering)的结果。滤波器的中心访问输人图像中的每个像素,就生成了处理(滤波)后的图像。
3.1空间相关与卷积
-
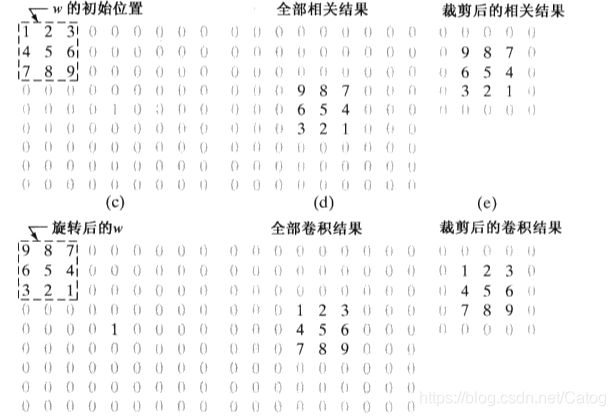
相关运算:在图像中移动核的中心,并在每个位置上计算乘积之和。卷积运算:将相关运算的核旋转180度,当核的值关于其中心对称时,相关和卷积得到的结果相同。
-
为理解相关与卷积的差别,我们在一维上进行示范,对离散单位冲激函数进行相关和卷积操作。可以看到,相关后得到一个核的旋转版本,卷积后得到一个核的副本。
-
相关操作可以表示为:相关操作不满足交换律和结合律

卷积操作可以表示为:卷积操作满足交换律和结合律,通常我们说的空间滤波视为卷积操作

3.1.1可分离滤波器核
-
空间滤波器核是一个矩阵,如果这个矩阵能表示为两个向量的外积(叉积),那么这个核就是可分离的。如:
w = [ 1 1 1 1 1 1 ] w=[111111][111111]w=[111111]
可以表示为两个向量的外积:
w = c r T = [ 1 1 ] [ 1 1 1 ] w=cr^T=[11][11][111][111]w=crT=[11][111]
-
大小为m × n m\times nm×n的可分离核可以表示为一个m × 1 m\times 1m×1和一个n × 1 n\times 1n×1的向量。对于大小为m × n m\times nm×n的核,在计算中需要M N m n MNmnMNmn次乘法和加法运算。而分离后的核共需要M N ( m + n ) MN(m+n)MN(m+n)次乘法和加法运算,减少了计算的时间。
-
根据矩阵理论,一个列向量和一个行向量相乘得到的矩阵,其秩总为1。因此要确定一个核是否可分离,只需确定其核为1.
离散单位脉冲函数 ( 离散单位冲击函数 ) 对应的 函数图像 如下 : 横轴是 t tt , 纵轴是 δ ( t ) \delta (t)δ(t) ;
3.2平滑滤波器
3.2.1盒式滤波器核
盒子滤波是一种非常有用的线性滤波。其系数的值一般都相同(通常为1)。
![]()
![]()
相关的MATLAB实现:
function imDst = boxfilter(imSrc, r)
% BOXFILTER O(1) time box filtering using cumulative sum
%
% - Definition imDst(x, y)=sum(sum(imSrc(x-r:x+r,y-r:y+r)));
% - Running time independent of r;
% - Equivalent to the function: colfilt(imSrc, [2*r+1, 2*r+1], 'sliding', @sum);
% - But much faster.
[hei, wid] = size(imSrc);
imDst = zeros(size(imSrc));
%cumulative sum over Y axis
imCum = cumsum(imSrc, 1);
%difference over Y axis
imDst(1:r+1, :) = imCum(1+r:2*r+1, :);
imDst(r+2:hei-r, :) = imCum(2*r+2:hei, :) - imCum(1:hei-2*r-1, :);
imDst(hei-r+1:hei, :) = repmat(imCum(hei, :), [r, 1]) - imCum(hei-2*r:hei-r-1, :);
%cumulative sum over X axis
imCum = cumsum(imDst, 2);
%difference over Y axis
imDst(:, 1:r+1) = imCum(:, 1+r:2*r+1);
imDst(:, r+2:wid-r) = imCum(:, 2*r+2:wid) - imCum(:, 1:wid-2*r-1);
imDst(:, wid-r+1:wid) = repmat(imCum(:, wid), [1, r]) - imCum(:, wid-2*r:wid-r-1);
end
该例子的核尺寸:7*7
处理前:![]()
处理后:
![]()
3.2.2低通高斯滤波器核
- 高斯核是唯一的可分离的圆对称核,高斯核的生成是通过以下公式得到的:( x , y ) (x,y)(x,y)是点的坐标,x 2 + y 2 x2+y2x2+y2表示点到中心的距离的平方。要产生高斯核,首先确定σ \sigmaσ的大小,然后规定核的大小,每个点的系数就根据坐标值来计算,最后将核的系数除以各个系数之和。

- 高斯核的系数,在到均值的距离大于3 σ 3\sigma3σ的位置,高斯函数的值就可以小到可以忽略,这意味我们选取高斯核的大小的时候应该不能大于6 σ × 6 σ 6\sigma\times6\sigma6σ×6σ。
- 两个高斯函数的乘积和卷积也是高斯函数,我们在给出两个一维高斯函数f 和 g f和gf和g的均值和标准差,其乘积和卷积得到的高斯函数的均值和标准差可以直接计算得出。

实例:
低通高斯滤波器函数:
function [image_out] = GLPF(image_in,D0)
%GLPF为高斯低通滤波器,D0为截止频率
%输入为需要进行高斯低通滤波的灰度图像,输出为经过滤波之后的灰度图像
f=image_in;
f=im2double(f);
% 1、给定一副大小为M×N的输入图像f(x,y),得到填充参数P=2M,Q=2N
M=size(f,1); N=size(f,2);
P=2*M; Q=2*N;
% 2、对输入图像f(x,y)添加必要数量的0,形成大小为P×Q的填充图像fp(x,y)
fp=zeros(P,Q);
fp(1:M,1:N)=f(1:M,1:N);
% 3、用(-1)^(x+y)乘以fp(x,y)移到其变换的中心
for i=1:P
for j=1:Q
fp(i,j)=(-1)^(i+j)*double(fp(i,j));
end
end
% 4、计算来自步骤3的图像的DFT,得到F(u,v)
F=fft2(fp,P,Q);
% 5、生成一个实的、对称的滤波函数H(u,v),其大小为P×Q,中心在(P/2,Q/2)处。用阵列相乘形成乘积G(u,v)=H(u,v)F(u,v)
H=zeros(P,Q);
a=2*(D0^2);
for u=1:P
for v=1:Q
D=(u-P/2)^2+(v-Q/2)^2;
H(u,v)=exp(-D./a);
end
end
G=F.*H; %频率域滤波
% 6、得到处理后的图像
gp=ifft2(G); %频域转换到时域图像
gp=real(gp);
for i=1:P
for j=1:Q
gp(i,j)=(-1)^(i+j)*double(gp(i,j));
end
end
% 7、通过从gp(x,y)的左上象限提取M×N区域,得到最终处理结果g(x,y)
image_out=gp(1:M,1:N);
end
函数调用:
clear all; close all; clc;
% 字符识别的应用
A=imread('G:\picture\Fig0419(a)(text_gaps_of_1_and_2_pixels).tif');
out1=GLPF(A,80);
figure;
subplot(1,2,1); imshow(A); title('低分辨率文本');
subplot(1,2,2); imshow(out1); title('DLPF滤波的结果');
%“美容”处理
B=imread('G:\picture\Fig0450(a)(woman_original).tif');
out2=GLPF(B,100);
out3=GLPF(B,80);
figure;
subplot(1,3,1); imshow(B); title('原图像');
subplot(1,3,2); imshow(out2); title('D0=100的GLPF');
subplot(1,3,3); imshow(out3); title('D0=80的GLPF');
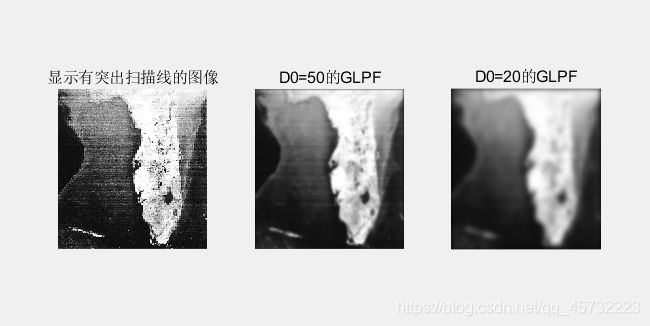
%卫星图像和航空图像的处理
C=imread('G:\picture\Fig0451(a)(satellite_original).tif');
out4=GLPF(C,50);
out5=GLPF(C,20);
figure;
subplot(1,3,1); imshow(C); title('显示有突出扫描线的图像');
subplot(1,3,2); imshow(out4); title('D0=50的GLPF');
subplot(1,3,3); imshow(out5); title('D0=20的GLPF');
实验结果图:
3.2.3统计排序(非线性)滤波器
我们把以白点和黑点形式叠加到图像上的冲击噪声称为椒盐噪声。
非线性滤波器最知名的是中值滤波:
它是一种邻域运算,类似于卷积,但计算的不是加权求和,而是把邻域中的像素按灰度级进行排序,然后选择该组的中间值作为输出像素值。
代码例子:
matlab自带的中值滤波函数为medfilt2(A,[M N]),A为要处理的图像,[M,N]表示模板的大小
%自编程实现中值滤波
clear;
n=5; %模板大小
image = imread('peppers.png');
I=rgb2gray(image);
J=imnoise(I,'salt',0.02);
[height, width] = size(J); %获取图像尺寸
FilterMid = J;
for row = (n+1)/2:height-(n-1)/2
for col = (n+1)/2:width-(n-1)/2
temp = double(J(row-((n-1)/2):row+((n-1)/2),...
col-((n-1)/2):col+((n-1)/2))); %获取模板区域
%中值滤波
template2 = sort(temp(:)); %对模板区域内像素值进行排序
FilterMid(row, col) = template2((n*n+1)/2); %更新模板中心像素值
end
end
figure ,subplot(1,3,1),imshow(I),title('原图像');
subplot(1,3,2),imshow(J),title('加入椒盐噪声后的图像');
subplot(1,3,3),imshow(FilterMid),title('中值滤波后的结果');
![]()
3.2.4锐化(高通)空间滤波器
3.2.4.1基础
首先,定义下一阶和二阶导数。
一维函数f ( x ) f(x)f(x)的一阶导数的基本定义是差分
![]()
一阶导数必须满足:
1.恒定灰度区域的一阶导数必须为0
2.灰度台阶或斜坡开始处的一阶导数必须非0
3.灰度斜坡上的一阶导数必须非0
二阶导数的任何定义都必须满足:
1.恒定灰度区域的二阶导数必须为0
2.灰度台阶或斜坡的开始处的二阶导数必须为0
3.灰度斜坡上的二阶导数必须为0
3.2.4.2二阶导数锐化图像——拉普拉斯
最简单的各向同性导数算子是拉普拉斯,定义为
![]()
套入上面所说的二阶导数
![]()
实例:
function [g_1,g_2] = Laplace1(A)
%拉普拉斯变换
%预先留出输出图像
A_double = double(A);
g_1 = A;
g_2 = A;
[ra,ca] = size(A);
%中心为负,最后应相减
%h1是x轴和y轴方向的二阶导数
%h2是四个方向的二阶导数
h1 = [0,1,0;1,-4,1;0,1,0];
h2 = [1,1,1;1,-8,1;1,1,1];
st = 3;
for A_i = (st+1)/2:ra-(st+1)/2+1
for A_j = (st+1)/2:ca-(st+1)/2+1
Hxy_1 = A_double(A_i-(st-1)/2:A_i+(st-1)/2,A_j-(st-1)/2:A_j+(st-1)/2).*h1;
Hxy_2 = A_double(A_i-(st-1)/2:A_i+(st-1)/2,A_j-(st-1)/2:A_j+(st-1)/2).*h2;
g_1(A_i,A_j) = sum(Hxy_1(:));g_2(A_i,A_j) = sum(Hxy_2(:));
end
end
%对于超出0-255范围的值应加以归0或归255
g_1 = uint8(A-g_1);
g_1(g_1<0) = 0;g_1(g_1>255) = 255;
g_2 = uint8(A-g_2);
g_2(g_2<0) = 0;g_2(g_2>255) = 255;
figure,
subplot(131),imshow(A),title("原图");
subplot(132),imshow(g_1),title("模板一锐化");
subplot(133),imshow(g_2),title("模板二锐化");
end
3.2.4.3一阶导数锐化图像——梯度
梯度算子
设图像为f(x,y), 定义为f(x,y)在点(x,y)的梯度矢量为G[f(x,y)]:
![]()
性质:
1)梯度的方向是在f(x,y)的最大变化率方向上
2)梯度的幅度用G[f(x,y)]表示:
![]()
梯度
对于数字图像:
![]()
简化为:
![]()
实例:
robert算子:
Robert算子对细节反映较敏感,但提取到的信息量较少,中心位置不明显,图像处理后的边缘不是很平滑。Roberts算子采用对角线方向相邻两像素之差近似梯度幅值检测边缘。检测水平和垂直边缘的效果好于斜向边缘,定位精度高,对噪声敏感。
clc;
I1=imread('D:\01.jpg'); %读取图像
%I1=rgb2gray(I); %将彩色图变成灰色图
subplot(1,3,1);
imshow(I1),title('原图','fontsize',16);
mode=[0,-1;
1,0];
[m,n]=size(I1);
I2=double(I1);
for i=2:m-1
for j=2:n-1
I2(i,j)=I1(i+1,j)-I1(i,j+1);
end
end
subplot(1,3,2);
imshow(I2),title('边缘提取后的图像','fontsize',16);
I3=I1;
for i=2:m-1
for j=2:n-1
I3(i,j)=I1(i+1,j)-I1(i,j+1)+I1(i,j);
end
end
subplot(1,3,3);
imshow(uint8(I3)),title('锐化后的图像','fontsize',16);
sobel算子
Sobel算子主要用作边缘检测,在技术上,它是一离散性差分算子,用来运算图像亮度函数的灰度之近似值。在图像的任何一点使用此算子,将会产生对应的灰度矢量或是其法矢量。Sobel算子根据像素点上下、左右邻点灰度加权差,在边缘处达到极值这一现象检测边缘。对噪声具有平滑作用,提供较为精确的边缘方向信息,边缘定位精度不够高。当对精度要求不是很高时,是一种较为常用的边缘检测方法。Sobel算子引入了平均因素,增强了最近的像素影响,噪声抑制效果比Prewitt算子要好。
clc;
I1=imread('D:\02.jpg'); %读取图像
%I1=rgb2gray(I); %将彩色图变成灰色图
subplot(1,3,1);
imshow(I1),title('原图','fontsize',16);
mode=[-1,0,1;
-2,0,2;
-1,0,1];
[m,n]=size(I1);
I2=double(I1);
for i=2:m-1
for j=2:n-1
I2(i,j)=I1(i+1,j+1)+2*I1(i,j+1)-I1(i+1,j-1)+I1(i-1,j+1)-2*I1(i,j-1)-I1(i-1,j-1);
end
end
subplot(1,3,2);
imshow(I2),title('边缘提取后的图像','fontsize',16);
I3=double(I1);
for i=2:m-1
for j=2:n-1
I3(i,j)=I1(i+1,j+1)+2*I1(i,j+1)-I1(i+1,j-1)+I1(i-1,j+1)-2*I1(i,j-1)-I1(i-1,j-1)+I1(i,j);
end
end
subplot(1,3,3);
imshow(uint8(I3)),title('锐化后的图像','fontsize',16);
3.2.5低通、高通、带阻、和带通滤波器
后三类滤波器都可以由低通滤波器构建。这里不做过多详细说明带阻和带通了,低通和高通前面已经讲过了。
4.频率域滤波
4.1傅里叶变换基础
直观理解:
直观上,傅里叶变换也是建立了一个坐标系,坐标系的基两两正交(这将在下面做出证明),任何一个信号都可以用这个坐标系中的基来进行分解与合成:
![]()
即为这个坐标系下的基,不同ω下![]()
两两正交
这里推荐看2004年出版的一本名叫《傅里叶变换》的书,上面讲的比较直观。
- 频道:就是频率的通道,不同的频道就是将不同的频率作为一个通道来进行信息传输。
- 很多在时域看似不可能做到的数学操作,在频域相反很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分,这在工程上称为滤波,是信号处理最重要的概念之一,只有在频域才能轻松的做到。
- 再说一个更重要,但是稍微复杂一点的用途——求解微分方程。微分方程的重要性不用我过多介绍了。各行各业都用的到。但是求解微分方程却是一件相当麻烦的事情。因为除了要计算加减乘除,还要计算微分积分。而傅里叶变换则可以让微分和积分在频域中变为乘法和除法。
-
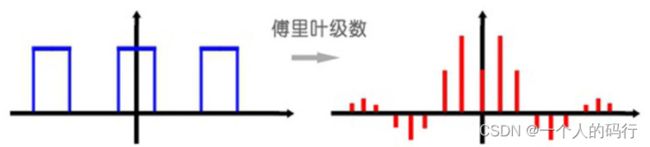
傅里叶级数的本质是将一个周期的信号分解成无限多分开的(离散的)正弦波
-
傅里叶变换,则是将一个时域非周期的连续信号,转换为一个在频域非周期的连续信号。
![]()
上面这个图转载自微博@花生油工人。
- 傅里叶变换实际上是对一个周期无限大的函数进行傅里叶变换。
4.2单变量的离散傅里叶变换
离散傅里叶变换公式:
根据公式,单变量离散傅里叶变是换将一维数组变换为傅里叶频率。设定一个大小为N的数组,t为X轴上的变量,取值为[0,n-1],f(t)为t=x出的值,计算机处理时,t即为输入数组下标index,f(t)为index对应位置数组中的值。
当μ=0时:
相当于整个输入数组直接求和。由于傅里叶变换计算涉及复数,可以将输入数组变换为复数形式,f(t)作为复数实部,虚部为0。根据欧拉公式:
![]()
在进行实际使用时,可将傅里叶变换为如下形式:
由于j为虚数,在实际计算过程中j=√-1是没有代入的,只需要计算复数的实部和虚数实部即可。
4.3二变量函数的傅里叶变换
![]()
实例:
1.主要函数介绍
主要用到的函数是fft2,其基本语法为:
Y = fft2(X)
它的含义是使用快速傅里叶变换算法返回矩阵的二维傅里叶变换, 这等同于计算fft(fft(X).‘).’。如果X是一个多维数组, fft2将采用高于 2 的每个维度的二维变换。输出Y的大小与X相同
Y = fft2(X,m,n)
将截断X或用尾随零填充X,以便在计算变换之前形成m×n矩阵。Y是m×n矩阵。如果X是一个多维数组,fft2将根据m和n决定X的前两个维度的形状,也就是说使用该语法fft2将使用所要求的0的个数对输入图像进行填充,以便结果函数的大小为m*n。
傅里叶频谱可以使用函数abs来获得:
S = abs(F)
该函数计算数组的每一个元素的幅度(实部和虚部平方和的平方根)。
2.程序实践
Step1:导入图像并显示
N=100
f=zeros(50,50);
f(15:35,23:28)=1;
subplot(2,3,1);
imshow(f);
title('原始图像')
Step2:计算傅里叶变换并显示其频谱
g= fft2(f); % matlab自带函数,来用对比
subplot(2,3,2);
imshow(real(g)); % 一般只要实部
title('fft2生成的"频域"图像');
S=abs(g);
subplot(2,3,3);
imshow(S)
title('傅里叶频谱')
Step3:居中频谱
Fc=fftshift(real(S)); %将零频分量移到频谱中心
subplot(2,3,4);
imshow(Fc)
title('居中的频谱')
Step4:使用对数变换进行视觉上的增强
S2=log(1+abs(Fc));
subplot(2,3,5);
imshow(S2)
title('使用对数变换进行视觉增强后的频谱');
4.4二维DFT和IDFT的一些性质
![]()
空间间隔和频率间隔的关系
频率域中样本之间的间隔,与空间样本之间的间隔及样本数量成反比。假设对连续函数 f(t,z) 取样生成了一幅数字图像 f(x,y) ,它有分别在 t 方向和 z 方向所取的 M×N 个样本组成。令 ΔT 和 ΔZ 表示样本间的间隔。
于是,频率域对应的离散变量间的间隔分别为:
![]()
旋转和平移
平移不影响 F(u,v) 的幅度(谱)。
使用极坐标
x=rcosθ,y=rsinθ,u=ωcosθ,v=ωsinθ
可得到如下变换对:
f(r,θ+θ0)⇔F(ω,φ+θ0)
它指出,若 f(x,y) 旋转 θ0 角度,则 F(u,v) 也旋转相同的角度;反之,若 F(u,v) 旋转某个角度, f(x,y) 也旋转相同的角度。
周期性
如一维情况中那样,二维傅里叶变换及其反变换在 u 方向和 v 方向是无限周期的,即:
上式中, k1 和 k2 是整数。
对称性
任意的实函数或复函数 w(x,y) 均可以表示为奇数部和偶数部之和,其中奇数部和偶数部既可以是实数,又可以是复数:
w(x,y)=we(x,y)+wo(x,y)
式中,对于 x 和 y 的所有有效值,偶数部和奇数部定义如下:
根据上面的定义有:
也就是说,偶函数是对称的,奇函数是反对称的。因为DFT和IDFT中的所有指数都是非负的整数,所以当我们谈论对称性(反对称性)时,指的是关于序列中心点的对称性(反对称性),此时,奇数部和偶数部的定义变为:

式中, x=0,1,2,…,M−1 , y=0,1,2,…,N−1 , M 和 N 照例分别是二维阵列的行数和列数。
由初等数学分析可知,两个偶函数的积或两个奇函数的积是偶函数,而一个偶函数和一个奇函数的积是奇函数。另外,离散函数是奇函数的唯一条件是其所有样本之和为零。这些性质导致了一个重要的结论,即对于任意两个离散的偶函数 we 和奇函数 wo ,有:
函数可以是实函数,也可以是复函数。
利用前面的概念,我们可以建立DFT及其反变换的许多重要的对称性质。频繁用到的一个性质是,实函数 f(x,y) 的傅里叶变换是共轭对称的,虚函数 f(x,y) 的傅里叶变换也是共轭对称的,即:
F∗(u,v)=F(−u,−v)
F∗(−u,−v)=−F(u,v)
傅里叶频谱和相角
因为二维DFT通常是复数,因此可以用极坐标来表示:
式中 ,幅度
称为傅里叶频谱(或频谱),而
![]()
称为相角或相位谱。 arctan 必须使用一个四象限反正切函数来计算,如MATLAB中的 atan2(Imag,Real) 函数。
最后,功率谱定义为:
P(u,v)=|F(u,v)|2=R2(u,v)+I2(u,v)
4.5低通频率域滤波器平滑图像
本节包括三类低通滤波器:理想低通滤波器,巴特沃斯滤波器,高斯低通滤波器。
4.5.1理想低通滤波器(ILPF)
在以原点为中心的一个圆内无衰减地通过所有频率,而在这个圆外“截止”所有的频率的二维低通滤波器。
实例:
close all;
clear all;
clc;
I = imread('football.jpg');
I=rgb2gray(I);
subplot(131),imshow(I);
title('原始图像');
I=imnoise(I,'gaussian');%加入高斯白噪声
subplot(132),imshow(I);
title('加入噪声后所得图像');
% 函数fft2()用于计算二维傅立叶变换
% 函数fftshift()是对函数fft2()作傅里叶变换后得到的频谱进行平移,将变换后的图像频谱中心从矩阵的原点移到矩阵的中心
% 作二维傅里叶变换前一定要用函数im2double()把原始图像的数据类型由uint8转化为double类型
% 否则会因为unit8数据类型只能表示0-255的整数而出现数据截断,进而出现错误结果
s=fftshift(fft2(im2double(I)));
[a,b]=size(s);
a0=round(a/2);
b0=round(b/2);
d0=50; % 将理想低通滤波器的截止频率D0设置为50
for i=1:a %双重for循环计算频率点(i,j)与频域中心的距离D(i,j)=sqrt((i-round(a/2)^2+(j-round(b/2)^2))
for j=1:b
distance=sqrt((i-a0)^2+(j-b0)^2);
if distance<=d0 % 根据理想低通滤波器产生公式,当D(i,j)<=D0,置为1
h=1;
else
h=0; % 根据理想低通滤波器产生公式,当D(i,j)>D0,置为0
end
s(i,j)=h*s(i,j);% 频域图像乘以滤波器的系数
end
end
% real函数取元素的实部
s=real(ifft2(ifftshift(s)));% 最后进行二维傅里叶反变换转换为时域图像
subplot(133),imshow(s,[]);
title('理想低通滤波所得图像');
4.5.2巴特沃斯低通滤波器
- 特点
- 较高的n nn值来控制这个BLPF函数可逼近ILPF的特性
- 较低的n nn值来控制这个BLPF函数可逼近GLPF的特性,同时提供从低频到高频的平滑过渡。
- 可用BLPF以小得多的振铃效应来逼近ILPF函数的清晰度
实例:
close all;
clear all;
clc;
I = imread('football.jpg');
I=rgb2gray(I);
subplot(131),imshow(I);
title('原始图像');
I=imnoise(I,'gaussian');%加入高斯白噪声
subplot(132),imshow(I);
title('加入噪声后所得图像');
% 函数fft2()用于计算二维傅立叶变换
% 函数fftshift()是对函数fft2()作傅里叶变换后得到的频谱进行平移,将变换后的图像频谱中心从矩阵的原点移到矩阵的中心
% 作二维傅里叶变换前一定要用函数im2double()把原始图像的数据类型由uint8转化为double类型
% 否则会因为unit8数据类型只能表示0-255的整数而出现数据截断,进而出现错误结果
s=fftshift(fft2(im2double(I)));
[N1,N2]=size(s);%求二维傅里叶变换后图像大小
n=2; % 将巴特沃斯低通滤波器的阶数n设置为2
d0=30; % 将巴特沃斯低通滤波器的截止频率D0设置为30
n1=round(N1/2);
n2=round(N2/2);
for i=1:N1 %双重for循环计算频率点(i,j)与频域中心的距离D(i,j)=sqrt((i-round(N1/2)^2+(j-round(N2/2)^2))
for j=1:N2
distance=sqrt((i-n1)^2+(j-n2)^2);
if distance==0
h=0;
else
h=1/(1+(distance/d0)^(2*n));% 根据巴特沃斯低通滤波器公式为1/(1+[D(i,j)/D0]^2n)
end
s(i,j)=h*s(i,j);% 频域图像乘以滤波器的系数
end
end
% real函数取元素的实部
s=real(ifft2(ifftshift(s)));% 最后进行二维傅里叶反变换转换为时域图像
subplot(133),imshow(s,[]);
title('Butterworth低通滤波图像');
4.5.3高斯低通滤波器(GLPF)
D0是截止频率。当D ( u , v ) = D 0 D(u, v) = D_0D(u,v)=D0时,GLPF传递函数下降到其最大值1.0的0.607。
close all;
clear all;
clc;
I = imread('football.jpg');
I=rgb2gray(I);
subplot(131),imshow(I);
title('原始图像');
I=imnoise(I,'gaussian');%加入高斯白噪声
subplot(132),imshow(I);
title('加入噪声后所得图像');
% 函数fft2()用于计算二维傅立叶变换
% 函数fftshift()是对函数fft2()作傅里叶变换后得到的频谱进行平移,将变换后的图像频谱中心从矩阵的原点移到矩阵的中心
% 作二维傅里叶变换前一定要用函数im2double()把原始图像的数据类型由uint8转化为double类型
% 否则会因为unit8数据类型只能表示0-255的整数而出现数据截断,进而出现错误结果
s=fftshift(fft2(im2double(I)));
[a,b]=size(s);
d0=30; % 将高斯低通滤波器的截止频率D0设置为30
a0=round(a/2);
b0=round(b/2);
for i=1:a
for j=1:b
distance=sqrt((i-a0)^2+(j-b0)^2); % 根据高斯低通滤波器公式H(u,v)=e^-[D^2(u,v)/2*D0^2]
h=exp(-(distance*distance)/(2*(d0^2))); % exp表示以e为底的指数函数
s(i,j)=h*s(i,j);% 频域图像乘以滤波器的系数
end
end
s=real(ifft2(ifftshift(s)));% 最后进行二维傅里叶反变换转换为时域图像
subplot(133),imshow(s,[]);
title('高斯低通滤波图像');
对图像噪声的简单理解:噪声在图像上常表现为引起较强视觉效果的孤立像素点或像素块。一般, 噪声信号与研究的对象不相关,它以无用的信息形式出现,扰乱图像的可观测信息。通俗的说,噪声点其实在视觉上看上去让人感觉很难受,直观理解就是其和周围的像素点差异比较大,显得比较突兀,视觉看起来很不舒服。
4.6高通滤波器锐化图像
在这里可以由低通滤波器得到理想,高斯,巴特沃斯高通滤波器
1.理想高通滤波器
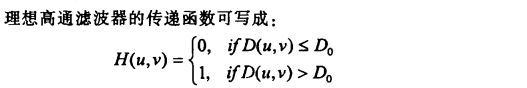
对理想高通滤波器,当频率平面上某点到原点的距离小于截止频率D0时,转移函数值为0,变换后的频率为0
实例:
close all;
clear all;
clc;
I = imread('coins.png');
subplot(121),imshow(I);
title('原始图像');
% 函数fft2()用于计算二维傅立叶变换
% 函数fftshift()是对函数fft2()作傅里叶变换后得到的频谱进行平移,将变换后的图像频谱中心从矩阵的原点移到矩阵的中心
% 作二维傅里叶变换前一定要用函数im2double()把原始图像的数据类型由uint8转化为double类型
% 否则会因为unit8数据类型只能表示0-255的整数而出现数据截断,进而出现错误结果
s=fftshift(fft2(im2double(I)));
[a,b]=size(s);
a0=round(a/2);
b0=round(b/2);
d0=50; % 将理想高通滤波器的截止频率D0设置为50
for i=1:a %双重for循环计算频率点(i,j)与频域中心的距离D(i,j)=sqrt((i-round(a/2)^2+(j-round(b/2)^2))
for j=1:b
distance=sqrt((i-a0)^2+(j-b0)^2);
if distance<=d0 % 根据理想高通滤波器产生公式,当D(i,j)<=D0,置为0
h=0;
else
h=1; % 根据理想高通滤波器产生公式,当D(i,j)>D0,置为1
end
s(i,j)=h*s(i,j);% 频域图像乘以滤波器的系数
end
end
% real函数取元素的实部
s=real(ifft2(ifftshift(s)));% 最后进行二维傅里叶反变换转换为时域图像
subplot(122),imshow(s,[]);
title('理想高通滤波所得图像');
2.巴特沃斯 (Butterworth)高通滤波器
实例:
close all;
clear all;
clc;
I = imread('coins.png');
subplot(121),imshow(I);
title('原始图像');
% 函数fft2()用于计算二维傅立叶变换
% 函数fftshift()是对函数fft2()作傅里叶变换后得到的频谱进行平移,将变换后的图像频谱中心从矩阵的原点移到矩阵的中心
% 作二维傅里叶变换前一定要用函数im2double()把原始图像的数据类型由uint8转化为double类型
% 否则会因为unit8数据类型只能表示0-255的整数而出现数据截断,进而出现错误结果
s=fftshift(fft2(im2double(I)));
[N1,N2]=size(s);%求二维傅里叶变换后图像大小
n=2; % 将巴特沃斯高通滤波器的阶数n设置为2
d0=30; % 将巴特沃斯高通滤波器的截止频率D0设置为30
n1=round(N1/2);
n2=round(N2/2);
for i=1:N1 %双重for循环计算频率点(i,j)与频域中心的距离D(i,j)=sqrt((i-round(N1/2)^2+(j-round(N2/2)^2))
for j=1:N2
distance=sqrt((i-n1)^2+(j-n2)^2);
if distance==0
h=0;
else
h=1/(1+(d0/distance)^(2*n));% 根据巴特沃斯高通滤波器公式为1/(1+[D0/D(i,j)]^2n)
end
s(i,j)=h*s(i,j);% 频域图像乘以滤波器的系数
end
end
% real函数取元素的实部
s=real(ifft2(ifftshift(s)));% 最后进行二维傅里叶反变换转换为时域图像
subplot(122),imshow(s,[]);
title('Butterworth高通滤波图像');
3.高斯高通滤波器
截止频率处在距频率矩形中心距离为D0的高斯高通滤波器GHPF的传递函数如下:
下图从左到右依次表示典型理想高通滤波器的透视图、图像表示和剖面图:
实例:
close all;
clear all;
clc;
I = imread('coins.png');
subplot(121),imshow(I);
title('原始图像');
% 函数fft2()用于计算二维傅立叶变换
% 函数fftshift()是对函数fft2()作傅里叶变换后得到的频谱进行平移,将变换后的图像频谱中心从矩阵的原点移到矩阵的中心
% 作二维傅里叶变换前一定要用函数im2double()把原始图像的数据类型由uint8转化为double类型
% 否则会因为unit8数据类型只能表示0-255的整数而出现数据截断,进而出现错误结果
s=fftshift(fft2(im2double(I)));
[a,b]=size(s);
d0=10; % 将高斯高通滤波器的截止频率D0设置为10
a0=round(a/2);
b0=round(b/2);
for i=1:a
for j=1:b
distance=sqrt((i-a0)^2+(j-b0)^2); % 根据高斯高通滤波器公式H(u,v)=e^-[D^2(u,v)/2*D0^2]
h=1-(exp(-(distance^2)/(2*(d0^2)))); % exp表示以e为底的指数函数
s(i,j)=h*s(i,j);% 频域图像乘以滤波器的系数
end
end
s=real(ifft2(ifftshift(s)));% 最后进行二维傅里叶反变换转换为时域图像
subplot(122),imshow(s,[]);
title('高斯高通滤波图像');
4.频率域中的拉普拉斯算子
拉普拉斯算子使用如下滤波器在频率与实现:
或者说关于频率矩形的中心,使用如下滤波器:
然后拉普拉斯图像由下式得到:
增强的话可用下式实现:
这里因为H(u,v)是负的,所以c=−1。频率域中上式可汇总为下面的式子:
实例:
im = imread('C:\Users\Administrator\Desktop\789.jpg');% 读取彩色图
subplot(131);
imshow(im);
title('原图');
%I=rgb2gray(RGB);
%imshow(I);
%title('原始灰度图像');
a=1;
model=[0 -2*a 0;-2*a 1+4*a -2*a;0 -2*a 0];
[m,n]=size(im);
Ig=im;
for i=2:m-1
for j=2:n-1
Ig(i,j)=(1+4*a).*im(i,j)-a.*(im(i+1,j)+im(i-1,j)+im(i,j+1)+im(i,j-1));
%Ig(i,j)=sum(sum(Ig));
end
end
Ig=Ig+im;
subplot(132);
imshow(uint8(Ig));
title('锐化后的图像');
Ig2=double(im); %将f转换归一化的double类图像,然后进行滤波
w=fspecial('laplacian',0);
g1=imfilter(im,w,'replicate');
g=im-g1;
subplot(133);
imshow(g);
title('matlab自带函数锐化');
5.同态滤波
照射-反射模型可用于开发一种频率域处理过程,该过程同时压缩灰度范围和增强对比度来改善一幅图像的表观,一幅图像可表示为其照射分量和反射分量的乘积:
但是傅里叶变换的乘积并不等于乘积的傅立叶变换,即:
![]()
但是我们可以定义:
则有:
即:
使用一个滤波器对Z(u,v)进行滤波:
空间域滤波后的图像:
根据定义有:
和
所以,滤波后空间域的图像可以写为:
最后,因为z(x,y)是通过取输入图像的自然对数形成的,可通过滤波后取指数来形成输出图像:
步骤总结如下:
该方法是以同态系统的一类系统的特殊情况为基础,方法的关键在于照射分量和反射分量的分离。图像的照射分量通常由慢的空间变化来表征,而反射分量往往引起突变,特别是在不同物体的连接部分。这样的特性导致图像取对数后的傅立叶变换的低频分量与照射相联系,而高频成分与反射相联系,虽然只是不强的联系。
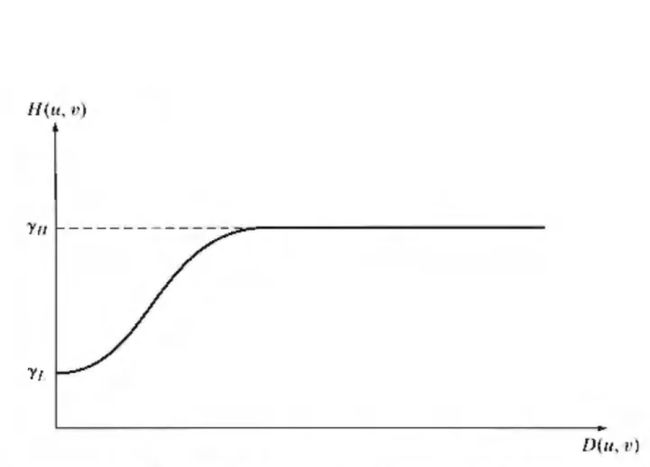
同态滤波函数如下:
其中如果且γL≤1且γH≥1那么如下图所示的滤波器趋向于衰减低频/照射分量的贡献,而增强高频/反射分量的贡献,常数c控制函数坡度的锐利度,在和γL和γH之间过渡,类似于高频强调滤波:
该滤波器实现起来也比较简单,不再重复。书中给出了一个同台滤波的例子如下所示,其中γL=0.25,γH=2,c=1,D0=80:
4.7快速傅里叶变换(FFT)
快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少,特别是被变换的抽样点数N越多,FFT算法计算量的节省就越显著。
它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的。
首先,二维DFT的可分离性,所有二维傅里叶变换的计算就可简化为多次执行计算一维DFT的一维算法。
快速傅里叶变换实例:
tp=0:2048; % 时域数据点数N
yt=sin(0.08*pi*tp).*exp(-tp/80); % 生成正弦衰减函数
plot(tp,yt), axis([0,400,-1,1]), % 绘正弦衰减曲线
t=0:800/2048:800; % 频域点数Nf
f=0:1.25:1000;
yf=fft(yt); % 快速傅立叶变换
ya=abs(yf(1:801)); % 幅值
yp=angle(yf(1:801))*180/pi; % 相位
yr=real(yf(1:801)); % 实部
yi=imag(yf(1:801)); % 虚部
figure
subplot(2,2,1)
plot(f,ya),axis([0,200,0,60]) % 绘制幅值曲线
title('幅值曲线')
subplot(2,2,2)
plot(f,yp),axis([0,200,-200,10]) % 绘制相位曲线
title('相位曲线')
subplot(2,2,3)
plot(f,yr),axis([0,200,-40,40]) % 绘制实部曲线
title('实部曲线')
subplot(2,2,4)
plot(f,yi),axis([0,200,-60,10]) % 绘制虚部曲线
title('虚部曲线')
相关变换的详细公式证明这里不再给出。
4.8选择性滤波
带阻滤波器和带通滤波器
这种类型的滤波器很容易使用前面的概念来构建,前面我们学习了理想、布特沃斯和高斯滤波器,则我们可以通过这些滤波器构建新的带阻滤波器
![]()
带通滤波器则为:
陷波滤波器
陷波滤波器是更有用的选择性滤波器可以有效的去除周期性噪声。陷波滤波器可以用高通滤波器的乘积来构造。一般形式为:
其中,H k ( u , v ) H_k(u,v)H**k(u,v)和H − k ( u , v ) H_{-k}(u,v)H−k(u,v)是高通滤波器。
距离的计算:
和
实例:
clc,clear,close all % 清理命令区、清理工作区、关闭显示图形
warning off % 消除警告
feature jit off % 加速代码运行
D0 = 4; % 阻止的频率点与频域中心的距离
u0 = 50;
v0 = 3;
im = imread(‘coloredChips.png’); % 原图像
R = imnoise(im(:,:,1),‘gaussian’,0,0.01); % R + 白噪声
G = imnoise(im(:,:,2),‘gaussian’,0,0.01); % G + 白噪声
B = imnoise(im(:,:,3),‘gaussian’,0,0.01); % B + 白噪声
im = cat(3,R,G,B); % 原图像 + 白噪声
H = freqfilter_gaussian_sink(2size(R,1),2size(R,2),u0,v0,D0); % 高斯陷波滤波器
R1 = fftfilt2(R,H); % 频域滤波
G1 = fftfilt2(G,H); % 频域滤波
B1 = fftfilt2(B,H); % 频域滤波
im1 = cat(3,R1,G1,B1);
im1 = uint8(im1);
figure(‘color’,[1,1,1])
subplot(121),imshow(im,[]); title(‘原始图像’)
subplot(122),imshow(im1,[]); title(‘高斯陷波滤波图像’);












![F(\mu )=\sum_{t=0}^{n}f(t)[cos(2\pi \mu t/n)-jsin(2\pi \mu t/n)]](http://img.e-com-net.com/image/info8/198805b040a54164ac52fe4631e1de63.gif)