python-numpy基础知识
参考资料：《跟着孙兴华学习Numpy基础》python Numpy 教程
笔记：
链接：https://pan.baidu.com/s/1m9g9An6JdOEWdtPiw6OIdA?pwd=xfc6
提取码：xfc6
--来自百度网盘超级会员V4的分享
中文官方：广播（Broadcasting） | NumPy 中文
链接：03.创建数组_哔哩哔哩_bilibili
一、安装Numpy模块
1、进入cmd命令界面
2、输入：pip install numpy
二、数组与矩阵的区别
- matrix是array的分支，两个可以通用，那就选择array，因为array更灵活，速度更快，很多人把二维的array也翻译成矩阵。
- 相同点：索引方式相同，都可以使用a[i][j]，a[i,j]进行索引
- matrix（矩阵）：具有相对简单的运算符号，比如两个matrix相乘（求内积），就是用符号*
- array（数组）：两个一维数组相乘用*，对应元素相乘
三、体验Numpy的便捷之处
题目： 数组a与数组b相加，数组a是1~N数字的立方，数组b是1~N数字的平方
import numpy as np
# python容器
def add_python(n):
a = [i ** 2 for i in range(1, n + 1)]
b = [i ** 3 for i in range(1, n + 1)]
c = list()
for i in range(n):
c.append(a[i] + b[i])
return c
# 利用Numpy
def add_numpy(n):
a = np.arange(1, n + 1) ** 3
b = np.arange(1, n + 1) ** 2
return a + b
print(add_python(4), add_numpy(4))结果：
接下进入正题！！！
四、数组
1 Numpy创建数组的方法
1.1 3种基础创建数组的方式
import numpy as np # 方式一 a = np.array([1, 2, 3]) # 方式二（常用的） b = np.arange(1, 4) # 方式三 c = np.array(range(1, 4)) print(a) print(b) print(b)
结果：
注意：
array：将输入数据（可以是列表、元组、数组以及其它序列）转换为ndarray(Numpy数组)，如不显示指明数据类型，将自动推断，默认复制所有输入数据。
arange：Python内建函数range的数组版，返回一个数组。
一个常见的错误，就是调用array的时候传入多个数字参数，而不是提供单个数字的列表类型作为参数。
>>> a = np.array(1,2,3,4) # WRONG
>>> a = np.array([1,2,3,4]) # RIGHT
1）array的属性
- shape：返回一个元组，表示 array的维度 [形状，几行几列] （2，3）两行三列，（2，2，3）两个两行三列。
import numpy as np a = np.array([1, 2, 3]) b = np.array([[1, 2], [4, 5]]) c = np.array([[[1, 2], [2, 6]], [[1, 2], [2, 6]], [[1, 2], [2, 6]], [[1, 2], [2, 6]]]) print(a.shape) print(b.shape) print(c.shape)
结果：
- ndim：返回一个数字，表示array的维度的数目
import numpy as np a = np.array([1, 2, 3]) b = np.array([[1, 2], [4, 5]]) c = np.array([[[1, 2], [2, 6]], [[1, 2], [2, 6]], [[1, 2], [2, 6]], [[1, 2], [2, 6]]]) print(a.ndim) print(b.ndim) print(c.ndim)
结果：
- size：返回一个数字，表示array中所有数据元素的数目
import numpy as np a = np.array([1, 2, 3]) b = np.array([[1, 2], [4, 5]]) c = np.array([[[1, 2], [2, 6]], [[1, 2], [2, 6]], [[1, 2], [2, 6]], [[1, 2], [2, 6]]]) print(a.size) print(b.size) print(c.size)
结果：
dtype：返回array中元素的数据类型
import numpy as np a = np.array([1, 2, 3]) b = np.array([[1, 2], [4, 5]]) c = np.array([[[1, 2], [2, 6]], [[1, 2], [2, 6]], [[1, 2], [2, 6]], [[1, 2], [2, 6]]]) print(a.dtype) print(b.dtype) print(c.dtype)
结果：
总结numpy的属性：
ndarray.ndim - 数组的轴（维度）的个数。在Python世界中，维度的数量被称为rank。
ndarray.shape - 数组的维度。这是一个整数的元组，表示每个维度中数组的大小。对于有 n 行和 m 列的矩阵，shape 将是 (n,m)。因此，shape 元组的长度就是rank或维度的个数 ndim。
ndarray.size - 数组元素的总数。这等于 shape 的元素的乘积。
ndarray.dtype - 一个描述数组中元素类型的对象。可以使用标准的Python类型创建或指定dtype。另外NumPy提供它自己的类型。例如numpy.int32、numpy.int16和numpy.float64。
ndarray.itemsize - 数组中每个元素的字节大小。例如，元素为 float64 类型的数组的 itemsize 为8（=64/8），而 complex32 类型的数组的 itemsize 为4（=32/8）。它等于 ndarray.dtype.itemsize 。
ndarray.data - 该缓冲区包含数组的实际元素。通常，我们不需要使用此属性，因为我们将使用索引访问数组中的元素。
1.2 arange创建数字序列
np.arange(上界，下界(娶不到)，步长，dtype="数据类型")
比如：np.arange(1, 5, 2, dtype="int64")
import numpy as np a = np.arange(1, 5, 2, dtype="int64") print(a) print(a.dtype)
结果：
当arange与浮点参数一起使用时，由于有限的浮点精度，通常不可能预测所获得的元素的数量。出于这个原因，通常最好使用linspace函数来接收我们想要的元素数量的函数，而不是步长（step）：
>>> from numpy import pi
>>> np.linspace( 0, 2, 9 ) # 9 numbers from 0 to 2
array([ 0. , 0.25, 0.5 , 0.75, 1. , 1.25, 1.5 , 1.75, 2. ])
>>> x = np.linspace( 0, 2*pi, 100 ) # useful to evaluate function at lots of points
>>> f = np.sin(x)
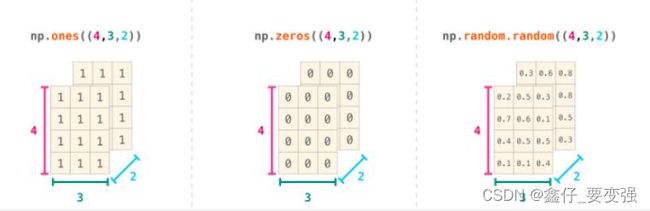
1.3 使用ones和 ones_like创建全是1的数组
1）np.ones(shape,dtype=None,order='C')
参数：
shape：整数或者整型元组定义返回数组的形状；可以是一个数（创建一维向量），也可以是一个元组（创建多维向量）
dtype : 数据类型，可选定义返回数组的类型。
order : {‘C’, ‘F’}, 可选规定返回数组元素在内存的存储顺序：C（C语言）-rowmajor；F（Fortran）column-major。
np.ones((a, b), dtype="float", order="C")
import numpy as np a = np.ones((1, 2), dtype='float', order="C") print(a) print(a.dtype)
结果：
2）ones_like创建形状相同的数组
返回：与a相同形状和数据类型的数组，并且数组中的值都为1.
np.ones_like(a,dtype=float,order='C',subok=True)
参数：
a：用a的形状和数据类型，来定义返回数组的属性
dtype ： 数据类型，可选
order顺序 ： {'C'，'F'，'A'或'K'}，可选,覆盖结果的内存布局。
subok ： bool，可选。True：使用a的内部数据类型，False：使用a数组的数据类型，默认为True
案例：
a = np.ones((3, 2), dtype='float', order="C") print(a) print(a.dtype) b = np.ones_like(a) print(b)
结果：
1.4 zeros和 zeros_like 创建全是0的数组
1）np.zeros(shape,dtype=None,order='C')
shape：整数或者整型元组定义返回数组的形状；可以是一个数（创建一维向量），也可以是一个元组（创建多维向量）
dtype : 数据类型，可选定义返回数组的类型。
order : {‘C’, ‘F’}, 可选规定返回数组元素在内存的存储顺序：C（C语言）-rowmajor；F（Fortran）column-major。
2）np.zeros(a,dtype=None)
# zeros创建全是0的数组，与ones创建的方式一样 # 方式一 a = np.zeros((3, 4), dtype="int32", order="C") # 方式二 b = np.zeros((4, 5)) print(a) print(b) # zeros_like创建形状相同的数组 a = np.zeros_like(b, dtype="int32", order='C') print(a) b = np.zeros_like(b) # 默认与b的数据类型一样 print(b)
结果：
1.5 full和full_like创建指定值的数组
1）np.full(shape,fill_value,dtype=None,order='C')
参数：
shape：整数或者整型元组定义返回数组的形状；可以是一个数（创建一维向量），也可以是一个元组（创建多维向量）
fill_value：标量（就是纯数值变量）
dtype : 数据类型，可选定义返回数组的类型。
order : {‘C’, ‘F’}, 可选规定返回数组元素在内存的存储顺序：C（C语言）-rowmajor；F（Fortran）column-major。
2）np.full_like(a,fill_value,dype=None)
案例：
# full创建指定值的数组 a = np.full((2, 2), fill_value=8, dtype="int64") print(a) # full_like 创建形状相同的指定的数组 a = np.full_like(a, fill_value='2') print(a)
结果：
1.6 使用random模块生成随机数组
np.random.seed(10):控制生成的元素的精度
mport numpy as np
import random
np.random.seed(10)
print(np.random.random()) # random.random()用来随机生成一个0到1之间的浮点数，包括零。
print(np.random.random())
print(np.random.random()) # 这里没有设置种子，随机数就不一样了
np.random.rand():返回[0,1]之间，从均匀分布中抽取样本
np.random.randn 返回标准正态分布随机数（浮点数）平均数0，方差1 【了解】
np.random.randint 随机整数
np.random.random 生成0.0至1.0的随机数
# 使用random模块生成随机数组 # 返回一个(或多个)来自“标准正态”分布的样本。 a = np.random.randn(2, 3) # 返回半开区间[0.0,1.0)内的随机浮点数。random_sample的别名，以方便向前移植到新的随机API。 b = np.random.random((2, 1)) # 返回从低(包含)到高(不包含)的随机整数。从指定dtype在“半开”区间(low, high)的“离散均匀”分布中返回随机整数。如果high为None(默认值)，则结果来自[0,low) c = np.random.randint(2, 4, (4, 5)) print(a) print(b) print(c) # round 设置数据精度 a = np.round(a, 2) print(a)
结果：
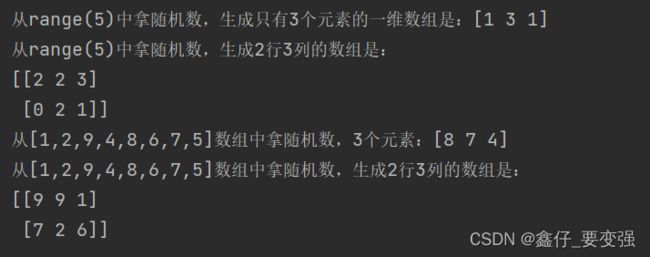
np.random.choice: 从一维数组中生成随机数
import numpy as np
a = np.random.choice(5, 3)
print(f'从range(5)中拿随机数，生成只有3个元素的一维数组是：{a}')
b = np.random.choice(5, (2, 3))
print(f'从range(5)中拿随机数，生成2行3列的数组是：\n{b}')
c = np.random.choice([1, 2, 9, 4, 8, 6, 7, 5], 3)
print(f'从[1,2,9,4,8,6,7,5]数组中拿随机数，3个元素：{c}')
d = np.random.choice([1, 2, 9, 4, 8, 6, 7, 5], (2, 3))
print(f'从[1,2,9,4,8,6,7,5]数组中拿随机数，生成2行3列的数组是：\n{d}')
结果：
np.random.shuffle（）(数组)把一个数进行随机排列
import numpy as np
一维数组 = np.arange(10)
print(f'没有随机排列前的一维数组{一维数组}')
np.random.shuffle(一维数组)
print('-'*50)
print(f'随机排列后的一维数组{一维数组}')
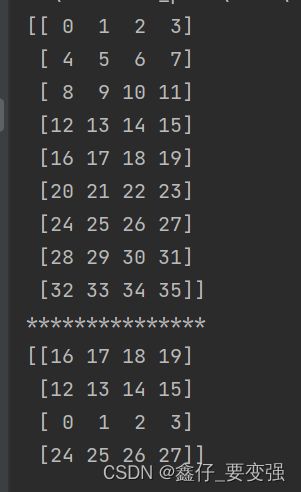
二维数组 = np.arange(20).reshape(4,5)
print('-'*50)
print(f'没有随机排列前的二维数组\n{二维数组}\n')
np.random.shuffle(二维数组)
print('-'*50)
print(f'随机排列后的二维数组\n{二维数组}') # 注意：多维数组随机排列只按行随机，列是不变的
print('-'*50)
三维数组 = np.arange(12).reshape(2,2,3)
print(f'没有随机排列前的三维数组\n{三维数组}\n')
print('-'*50)
np.random.shuffle(三维数组)
print(f'随机排列后的三维数组\n{三维数组}')结果：
permutation(数组) 把一个数组随机排列或者数字全排列
normal 生成正态分布数字：normal [平均值，方差，size]
uniform 均匀分布
补充：精度确定，保留小数点几位：np.round(a, 2)
2 多维数组
2.1 改变数组形状
1） reshape、ravel、resize不改值修改形状
例：
>>> a.ravel() # returns the array, flattened
array([ 2., 8., 0., 6., 4., 5., 1., 1., 8., 9., 3., 6.])
>>> a.reshape(6,2) # returns the array with a modified shape
array([[ 2., 8.],
[ 0., 6.],
[ 4., 5.],
[ 1., 1.],
[ 8., 9.],
[ 3., 6.]])
>>> a.T # returns the array, transposed
array([[ 2., 4., 8.],
[ 8., 5., 9.],
[ 0., 1., 3.],
[ 6., 1., 6.]])
该reshape函数返回带有修改形状的参数，而该 ndarray.resize方法会修改数组本身：
>>> a
array([[ 2., 8., 0., 6.],
[ 4., 5., 1., 1.],
[ 8., 9., 3., 6.]])
>>> a.resize((2,6))
>>> a
array([[ 2., 8., 0., 6., 4., 5.],
[ 1., 1., 8., 9., 3., 6.]])
如果在 reshape 操作中将 size 指定为-1，则会自动计算其他的 size 大小：
>>> a.reshape(3,-1)
array([[ 2., 8., 0., 6.],
[ 4., 5., 1., 1.],
[ 8., 9., 3., 6.]])
例：
np.arange(10).reshape(2,5) # 变成2行5列
a.reshape(10) # 变回1行1列
a.flatten() # 不清楚对方什么阵型，直接转一维
注意区别：
shape：返回数组的维度
reshape:不改变数组的值，修改形状
案例：
# reshape 不修改值修改形状
a = np.arange(10).reshape(2, 5)
print(a)
print('-------------')
b = a.reshape(10)
print(b)
c = a.flatten()
print('-------------')
print(c)
print('-------------')
print(a)
2） 将不同数组堆叠在一起
几个数组可以沿不同的轴堆叠在一起，例如：
np.vstack((a,b)) 按照行堆积
np.hstack((a,b)) 按照列堆积
该函数将column_stack 1D数组作为列堆叠到2D数组中。它仅相当于 hstack2D数组：
a = [ 8., 8., 1., 8.]
b = [ 0., 0., 0., 4.]
>>> np.column_stack((a,b)) # with 2D arrays
array([[ 8., 8., 1., 8.],
[ 0., 0., 0., 4.]])
# 区别
np.column_stack((a,b)) # returns a 2D array
array([[ 4., 3.],
[ 2., 8.]])
>>> np.hstack((a,b)) # the result is different
array([ 4., 2., 3., 8.])
另一方面，该函数ma.row_stack等效vstack 于任何输入数组。通常，对于具有两个以上维度的数组， hstack沿其第二轴vstack堆叠，沿其第一轴堆叠，并concatenate 允许可选参数给出连接应发生的轴的编号。
在复杂的情况下，r_和c c_于通过沿一个轴堆叠数字来创建数组很有用。它们允许使用范围操作符(“：”)。
与数组一起用作参数时， r_ 和 c_ 在默认行为上类似于 vstack 和 hstack ，但允许使用可选参数给出要连接的轴的编号。
3) 将一个数组拆分成几个较小的数组：
>>> a = np.floor(10*np.random.random((2,12)))
>>> a
array([[ 9., 5., 6., 3., 6., 8., 0., 7., 9., 7., 2., 7.],
[ 1., 4., 9., 2., 2., 1., 0., 6., 2., 2., 4., 0.]])
>>> np.hsplit(a,3) # Split a into 3 按照列切割
[array([[ 9., 5., 6., 3.],
[ 1., 4., 9., 2.]]), array([[ 6., 8., 0., 7.],
[ 2., 1., 0., 6.]]), array([[ 9., 7., 2., 7.],
[ 2., 2., 4., 0.]])]
>>> np.hsplit(a,(3,4)) # Split a after the third and the fourth column
[array([[ 9., 5., 6.],
[ 1., 4., 9.]]), array([[ 3.],
[ 2.]]), array([[ 6., 8., 0., 7., 9., 7., 2., 7.],
[ 2., 1., 0., 6., 2., 2., 4., 0.]])]
vsplit沿行分割，并array_split允许指定要分割的轴
2.2 数组计算
凡是形状一样的数组，假设数组a和数组b，可以直接用a+b、a-b、a*b、a/b。
# 数组计算
a = np.arange(10).reshape(2, 5)
b = np.random.randn(2, 5)
print(np.round(a+b, 2))
print('-----------------------------------')
print(np.round(a-b, 2))
print('------------------------------------')
print(np.round(a*b, 2))
print('-------------------------------------')
print(np.round(a/b, 2))
print('-------------------------------------')
print(np.round(a+2, 2))
print('-------------------------------------')
print(np.round(a*2, 2))
结果：
与许多矩阵语言不同，乘积运算符*在NumPy数组中按元素进行运算。矩阵乘积可以使用@运算符（在python> = 3.5中）或dot函数或方法执行：
>>> A = np.array( [[1,1],
... [0,1]] )
>>> B = np.array( [[2,0],
... [3,4]] )
>>> A * B # elementwise product
array([[2, 0],
[0, 4]])
>>> A @ B # matrix product
array([[5, 4],
[3, 4]])
>>> A.dot(B) # another matrix product
array([[5, 4],
[3, 4]])
当使用不同类型的数组进行操作时，结果数组的类型对应于更一般或更精确的数组（称为向上转换的行为）,b的精度高于a.
b += a(可以运行)
a += b （报错）
总结：
（1）形状一样的数组按对应位置进行计算。
（2）一维和多维数组是可以计算的，只要它们在某一维度上是一样的形状，仍然是按位置计算。
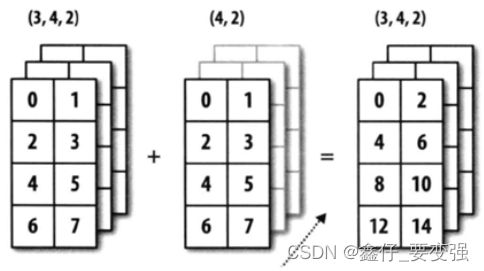
2.3 广播规则
基础知识：
广播的原则：
1）如果两个数组的后缘维度（trailing dimension，即从末尾开始算起的维度）的轴长度相符，或其中的一方的长度为1，则认为它们是广播兼容的。广播会在缺失和（或）长度为1的维度上进行。
2）这句话乃是理解广播的核心。广播主要发生在两种情况，一种是两个数组的维数不相等，但是它们的后缘维度的轴长相符，另外一种是有一方的长度为1。
数组维度不同，后缘维度的轴长相符：
例1
例二：
例三：
详细知识：
术语广播（Broadcasting）描述了 numpy 如何在算术运算期间处理具有不同形状的数组。受某些约束的影响，较小的数组在较大的数组上“广播”，以便它们具有兼容的形状。广播提供了一种矢量化数组操作的方法，以便在C而不是Python中进行循环。它可以在不制作不必要的数据副本的情况下实现这一点，通常导致高效的算法实现。然而，有些情况下广播是一个坏主意，因为它会导致内存使用效率低下，从而减慢计算速度。
NumPy 操作通常在逐个元素的基础上在数组对上完成。在最简单的情况下，两个数组必须具有完全相同的形状，如下例所示：
>>> a = np.array([1.0, 2.0, 3.0])
>>> b = np.array([2.0, 2.0, 2.0])
>>> a * b
array([ 2., 4., 6.])
当数组的形状满足某些约束时，NumPy的广播规则放宽了这种约束。当一个数组和一个标量值在一个操作中组合时，会发生最简单的广播示例：
>>> a = np.array([1.0, 2.0, 3.0])
>>> b = 2.0
>>> a * b
array([ 2., 4., 6.])
结果等同于前面的示例，其中b是数组。我们可以将在算术运算期间b被 拉伸 的标量想象成具有相同形状的数组a。新元素 b只是原始标量的副本。拉伸类比只是概念性的。NumPy足够聪明，可以使用原始标量值而无需实际制作副本，因此广播操作尽可能具有内存和计算效率。
第二个示例中的代码比第一个示例中的代码更有效，因为广播在乘法期间移动的内存较少（b是标量而不是数组）。
#一般广播规则
在两个数组上运行时，NumPy会逐元素地比较它们的形状。它从尾随尺寸开始，并向前发展。两个尺寸兼容时
- 他们是平等的，或者
- 其中一个是1
如果不满足这些条件，则抛出 ValueError: operands could not be broadcast together 异常，指示数组具有不兼容的形状。结果数组的大小是沿输入的每个轴不是1的大小。
数组不需要具有相同 数量 的维度。例如，如果您有一个256x256x3RGB值数组，并且希望将图像中的每种颜色缩放不同的值，则可以将图像乘以具有3个值的一维数组。根据广播规则排列这些数组的尾轴的大小，表明它们是兼容的：
Image (3d array): 256 x 256 x 3
Scale (1d array): 3
Result (3d array): 256 x 256 x 3
当比较的任何一个尺寸为1时，使用另一个尺寸。换句话说，尺寸为1的尺寸被拉伸或“复制”以匹配另一个尺寸。
在以下示例中，A和B数组都具有长度为1的轴，在广播操作期间会扩展为更大的大小：
A (4d array): 8 x 1 x 6 x 1
B (3d array): 7 x 1 x 5
Result (4d array): 8 x 7 x 6 x 53 数组切片与索引
3.1 数组的索引
1）一维数组的索引
import numpy as np a = np.arange(5) print(a[2:4:1])
结果：
2）二维数组
import numpy as np
a = np.arange(10).reshape((5, 2))
print(a)
print("-----------------------")
print(a[2, 1]) # 取数组a的2行2列，返回值5
print('------------------------')
print(a[-1, 1]) # 取数组a的5行2列，返回值9
print('------------------------')
print(a[:, 1]) # 取第2列
print('------------------------')
print(a[2, :]) # 取第三行
结果：
3）布尔索引
True(取值)，False(不取值)。
例1：
import numpy as np
数组 = np.arange(10)
print(数组)
筛选 = 数组 > 5
print(筛选) # 返加False和True
print(数组[筛选]) # 返回6 7 8 9 结果：
例2：把一维数组进行01化处理
import numpy as np
数组 = np.arange(10)
print(数组)
print('-'*25)
数组[数组<=5] = 0 # 小于5的重新赋值为0
数组[数组>5] = 1 # 大于5的重新赋值为1
print(数组)结果：
例三：二维数组
import numpy as np
数组 = np.arange(1, 21).reshape(4, 5)
print(数组)
print('*'*50)
筛选 = 数组>10
print(筛选) # 返回一个布尔数组，即有行又有列
print('*'*50)
print(数组[筛选]) # 返回所有为True的对应数字组成的数组，以一维数组展现结果：
例四：把第3例大于5的行筛选出来并重新赋值为520
import numpy as np
数组 = np.arange(1, 21).reshape(4, 5)
print(数组)
print("-"*30)
筛选 = 数组[:, 3] > 5 # 所有行第3列，大于5的
print(筛选)
数组[:, 3][筛选] = 520
print(数组)
结果：
3）神奇索引
使用整数数组进行数据索引
一维数组：
import numpy as np
a = np.arange(8)
b = a[[2, 3, 4]]
print(a)
print('*'*30)
print(b)
a[[2,3,4]] # 返回对应下标的一数组 array([2， 3， 4])
二维数组：
单个一维数组索引
import numpy as np
数组 = np.arange(36).reshape(9, 4)
print(数组)
print("*" * 15)
print(数组[[4, 3, 0, 6]]) # 返回第4行，第3行，第0行，第6行结果：
两个一维数组共同索引（必须是相同形状的），第一个一维数组对应行，第二个一维数组对应列。比如a[[1, 2], [2, 3]],那么第一个取得a数组中的位置是位于a[1, 2].
例：
import numpy as np
数组 = np.arange(32).reshape((8, 4))
print(数组)
读取 = 数组[[1, 5, 7, 2], [0, 3, 1, 2]] # 取第1行第0列，第5行第3列，第7行第1列，第2行第2列
print('-'*50)
print(读取)结果：
进阶：# 取所有行的，第1列和第2列
import numpy as np
数组 = np.arange(36).reshape(9, 4)
print(数组)
print("*" * 30)
print(数组[:, [1, 2]]) # 取所有行的，第1列和第2列
结果：
3.2 切片修改（注意：会修改原来的数组）
由于Numpy经常处理大数组，避免每次都复制，所以切片修改时直接修改了数组
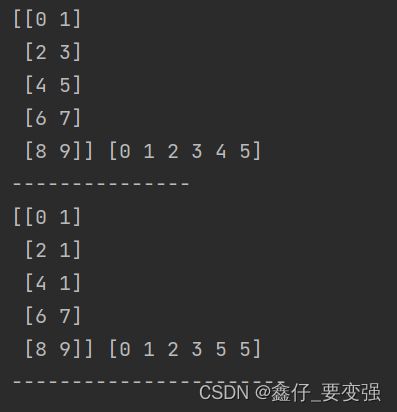
import numpy as np
a = np.arange(10).reshape((5, 2))
b = np.arange(6)
print(a, b)
print('---------------')
b[4:6] = 5
a[1:3, 1] = 1
print(a, b)
print("-----------------------")
结果：
当提供的索引少于轴的数量时，缺失的索引被认为是完整的切片（默认为:）
>>> b
array([[ 0, 1, 2, 3],
[10, 11, 12, 13],
[20, 21, 22, 23],
[30, 31, 32, 33],
[40, 41, 42, 43]])
>>> b[-1] # the last row. Equivalent to b[-1,:]
array([40, 41, 42, 43])
>>> a = [0 1 2 3]
array([0 1 2 3])
但是，如果想要对数组中的每个元素执行操作，可以使用flat属性，该属性是数组的所有元素的迭代器：
>>> for element in b.flat:
... print(element)
...
0
1
2
3
五、Numpy的轴
数组=np.array([[[1,2],[4,5],[7,8]],[[8,9],[11,12],[14,15]],[[10,11],[13,14],[16,17]],[[19,20],[22,23],[25,26]]])
print(数组.shape) # 返回 (4, 3, 2)
最内层一对 [ ] 可以代表一个1维数组
加粗的一对 [ ] 里面有3个一维数组，也就是2维数组
最外层的一对 [ ] 里面有3个2维数组也就是3维数组
0轴是行，1轴是列，2轴是纵深
数组的shape维度是（4,3,2），元组的索引为 [ 0,1,2 ]
假设维度是（2，3），元组的索引为[0,1]
假设维度是（4，） 元组的索引为[0]
可以看到轴编号和shape元组的索引是对等的，所以这个编号可以理解为高维nd.array.shape产生的元组的索引
我们知道shape（4,3,2）表示数组的维度，既然shape的索引可以看做轴编号，那么一条轴其实就是一个维度
0轴对应的是最高维度3维，1轴对应2维，2轴对应的就是最低维度的1维
总结：凡是提到轴，先看数组的维度，有几维就有几个轴
5.1 沿轴切片
首先看1个参数的切片操作：
数组[0:2]
这里有个很重要的概念， :2 是切片的第一个参数，约定俗成第一个参数就代表0轴
0轴表示2维，所以这个切片是在2维这个维度上切的，又叫“沿0轴切”。
这个2维数据是由3个1维数组组成的，这3个1维数组当然也有索引号也是[0,1,2]，[ :2 ] 就表示它要切取2维（0轴）上3个1维数组中的索引 [ 0 ] 和索引 [ 1 ] ，于是得到 ([ 1, 2, 3 ]) 和 ([ 4, 5, 6 ]) 这两个1维数组。
首先看2个参数的切片操作：
数组[:2,1:]
就是在两个维度（轴）上各切一刀，第1个参数就是2维（0轴）， :2 表示切取2维（0轴）上的索引 [ 0 ] 和索引 [ 1 ] ，即 ([ 1, 2, 3 ]) 和 ([ 4, 5, 6 ]) 这两个1维数组
第2个参数就是1维（1轴），1: 表示切取1维（1轴）上的索引 [ 1 ] 和索引 [ 2 ] ，即对数组 ([ 1, 2, 3 ]) 取 ([ 2,3 ]) ，对数组 ([ 4, 5, 6 ]) 取 ([ 5,6 ])
六、数组的相关操作
6.1数组的转置
1）行列转置
data.T和data.transpose()
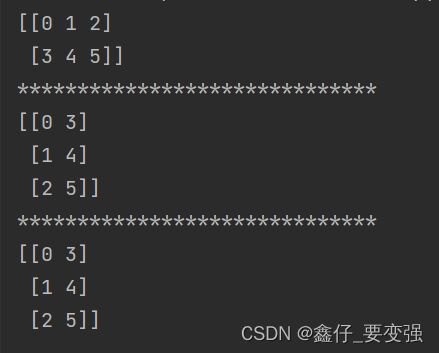
import numpy as np
数组 = np.arange(6).reshape(2, 3)
print(数组)
print("*" * 30)
# 方式一
print(数组.T)
print("*" * 30)
# 方式二
print(数组.transpose()) 结果：
2）列转置
data.swapaxes()
import numpy as np
数组 = np.arange(6).reshape(3, 2)
print(数组)
print("*" * 30)
# 形式一：保持不变
print(数组.swapaxes(1, 1))
print("*" * 30)
# 形式二：行转置
print(数组.swapaxes(0, 1))
print("*" * 30)
# 形式三：列转置
print(数组.swapaxes(1, 0))结果：
6.2 通函数
通函数也可以称为 ufunc， 是一种在 ndarray 数据中进行逐元素操作的函数。某些简单函数接受了一个或者多个标量数值，并产生一个或多个标量结果，而通用函数就是对这些简单函数的向量化封装。比如： argmax：返回沿轴的最大值的索引， argmin：返回沿轴的最大值的索引， argsort：返回对数组进行排序的索引， average：沿指定的轴计算加权平均数， bincount：非负整数数组中每个值的出现次数， ceil：从元素的角度返回输入的上限， clip：剪切(限制)数组中的值， conj：求共轭， corrcoef返回皮尔逊乘积矩相关系数。， cov根据数据和权重估计协方差矩阵。
有很多 ufunc 是简单的逐元素转换，比如 sqrt 和 exp 函数：就是一元通用函数
二元通用函数 比如： np.maximum(x ,y))# 对位比较大小，取大的，生成新的数组返回，逐个元素地将 x和 y 中元素的最大值计算出来 。
6.3 数学和统计函数
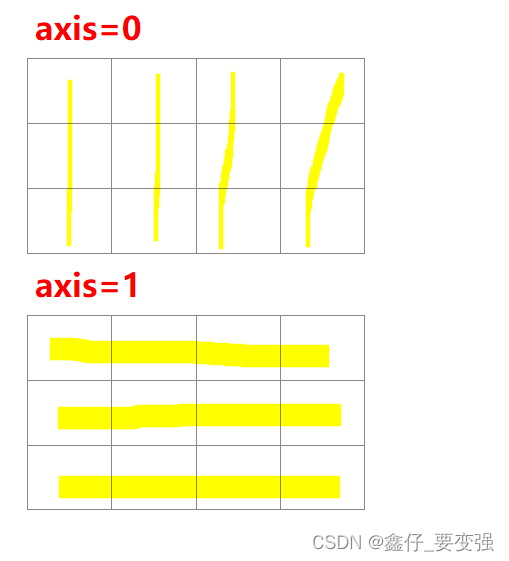
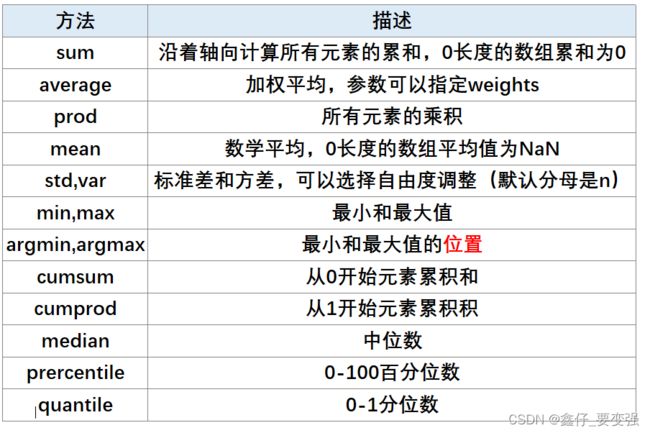特别注意这些函数在对二维数组操作时：
axis=0代表按照列计算所有行，axis=1代表按照行计算所有列。比如：np.sum(a,axis=0)
import numpy as np
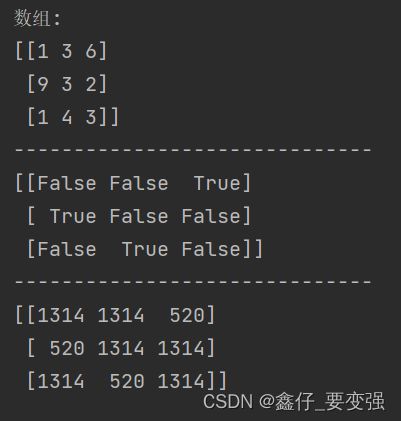
a = np.array([[1,3,6],[9,3,2],[1,4,3]])
print(f'数组:\n{a}')
print('-'*30)
print(np.sum(a,axis=0)) # 每行中的每个对应元素相加(即每列的各个行的和)，返回一维数组
print('-'*30)
print(np.sum(a,axis=1)) # 每列中的每个元素相加（即每行的各个列的和），返回一维数组结果：
特别注意：
其中思路正好是反的：axis=0 求每列的和。axis=1求每行的和。
补充：
数组对应到现实中的一种解释：
- 行：每行对应一个样本数据
- 列：每列代表样本的一个特征
数据标准化：
- 对于机器学习、神经网络来说，不同列的量钢是相同的，收敛更快。
- 有两个特征，一个是商品单价1元至50元，另一个是销售数量3千个至1万个，这两个数字不可比，所以需要都做标准化。
- 比如在Excel里，单价一个列，销售数量一个列，不同列代表不同特征，所以用axis=0做计算
- 标准化一般使用：通过均值和方差实现
数组 = （数组 - mean(数组，axis=0)）/ std(数组, axis=0)
6.4 数组条件筛选
1）将条件逻辑作为数组操作
例：
import numpy as np
a = np.array([[1, 3, 6], [9, 3, 2], [1, 4, 3]])
print(f'数组:\n{a}')
print('-' * 30)
print(a > 3) # 符合条件则为True,不符合则是False,返回一个相同形状的数组
print('-' * 30)
print(np.where(a > 3, 520, 1314)) # True则是520，False是1314结果：
2）布尔值索引数组方法
True取数组对应位置的值，False不取值。
例：
import numpy as np
a = np.array([[1, 3, 6], [9, 3, 2], [1, 4, 3]])
print(f'数组:\n{a}')
print('-' * 30)
print(a > 3) # 符合条件则为True,不符合则是False,返回一个相同形状的数组
print('-' * 30)
print(a[a > 3]) # True则是520，False是1314结果：
补充：对于布尔值数组，有两个常用方法any和all
any：检查数组中是否至少有一个True
all：检查是否每个值都是True
例：
import numpy as np
a = np.array([False,False,True,False])
print(a.any())
print('-'*50)
print(a.all())结果：
3）按照值的大小排序
ndarray.sort(axis=-1, kind='quicksort', order=None)
例：
import numpy as np
a = np.array([[0,12,48],[4,18,14],[7,1,99]])
print(f'数组：\n{a}')
print('-'*30)
print(np.sort(a)) # 默认按最后的轴排序，就是（行，列）（0，1）
print('-'*30)
print(np.sort(a,axis=0)) # 按行排序结果：
4）获取从大到小的元素的索引 argsort
numpy.argsort(a, axis=-1, kind='quicksort', order=None)
对数组沿给定轴执行间接排序，并使用指定排序类型返回数据的索引数组。 这个索引数组用于构造排序后的数组。
参数类似于sort()
一维数组：
import numpy as np
x = np.array([59, 29, 39])
a = np.argsort(x)
print(f'索引升序：{a}') # 升序
# argsort函数返回的是数组值从小到大的索引值,[3, 1, 2]从小到大为[1，2，3],期对应的索引为[1，2，0]
print(f'数组升序：{x[a]}') # 以排序后的顺序重构原数组
b = np.argsort(-x) # 降序
print(f'索引降序：{b}')
print(f'数组升序：{x[b]}')结果：
二维数组：
例：
import numpy as np
x = np.array([[0, 12, 48], [4, 18, 14], [7, 1, 99]])
a1 = np.argsort(x)
print(f'索引排序：\n{a1}')
print('-'*30)
# 以排序后的顺序重构原数组，注意与一维数组的形式不一样
print(np.array([np.take(x[i], x[i].argsort()) for i in range(3)]))结果：
5）唯一值与其它集合逻辑 unique和in1d
去重复：
import numpy as np
姓名 = np.array(['孙悟空','猪八戒','孙悟空','沙和尚','孙悟空','唐僧'])
print(np.unique(姓名))
数组 = np.array([1,3,1,3,5,3,1,3,7,3,5,6])
print(np.unique(数组))结果：
检查一个数组中的值是否在另外一个数组中，并返回一个布尔数组：
例：
import numpy as np
a = np.array([6,0,0,3,2,5,6])
print(np.in1d(a,[2,3,6]))结果：
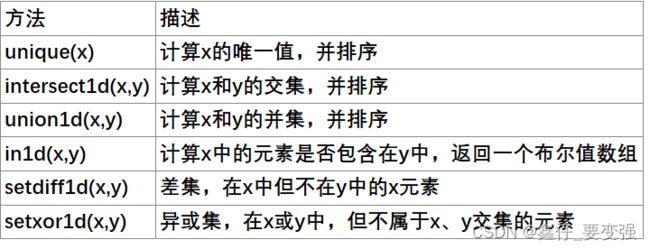
附：数组的集合操作 x和y是两个不同的数组
七、视图与拷贝
当计算和操作数组时，有时会将数据复制到新数组中，有时则不会。这通常是初学者混淆的根源。有三种情况：
#完全不复制
简单分配不会复制数组对象或其数据。
>>> a = np.arange(12)
>>> b = a # no new object is created
>>> b is a # a and b are two names for the same ndarray object
True
>>> b.shape = 3,4 # changes the shape of a
>>> a.shape
(3, 4)
Python将可变对象作为引用传递，因此函数调用不会复制。
>>> def f(x):
... print(id(x))
...
>>> id(a) # id is a unique identifier of an object
148293216
>>> f(a)
148293216
#视图或浅拷贝
不同的数组对象可以共享相同的数据。该view方法创建一个查看相同数据的新数组对象。
>>> c = a.view()
>>> c is a
False
>>> c.base is a # c is a view of the data owned by a
True
>>> c.flags.owndata
False
>>>
>>> c.shape = 2,6 # a's shape doesn't change
>>> a.shape
(3, 4)
>>> c[0,4] = 1234 # a's data changes
>>> a
array([[ 0, 1, 2, 3],
[1234, 5, 6, 7],
[ 8, 9, 10, 11]])
切片数组会返回一个视图：
>>> s = a[ : , 1:3] # spaces added for clarity; could also be written "s = a[:,1:3]"
>>> s[:] = 10 # s[:] is a view of s. Note the difference between s=10 and s[:]=10
>>> a
array([[ 0, 10, 10, 3],
[1234, 10, 10, 7],
[ 8, 10, 10, 11]])
#深拷贝
该copy方法生成数组及其数据的完整副本。
>>> d = a.copy() # a new array object with new data is created
>>> d is a
False
>>> d.base is a # d doesn't share anything with a
False
>>> d[0,0] = 9999
>>> a
array([[ 0, 10, 10, 3],
[1234, 10, 10, 7],
[ 8, 10, 10, 11]])
有时，如果不再需要原始数组，则应在切片后调用 copy。例如，假设a是一个巨大的中间结果，最终结果b只包含a的一小部分，那么在用切片构造b时应该做一个深拷贝：
>>> a = np.arange(int(1e8))
>>> b = a[:100].copy()
>>> del a # the memory of ``a`` can be released.
如果改为使用 b = a[:100]，则 a 由 b 引用，并且即使执行 del a 也会在内存中持久存在。