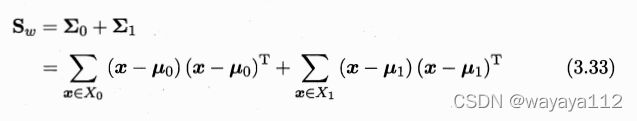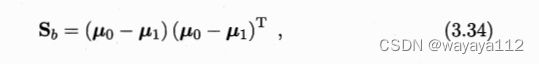【机器学习-西瓜书】第3章-线性模型
3.1 基本形式
示例x由 d个属性描述，
线性模型 试图学得一个通过属性的线性组合来进行预测的函数，即
3.2 线性回归
3.2.1 一元线性回归：for regression
给定数据集 
先考虑最简单的情形：输入只有一个属性，此时线性回归试图学得: 
使得
.
如何确定w和b？=> 让均方误差最小化，即
基于均方误差最小化进行模型求解的方法，称为“最小二乘法 (Least Square Method)”。即找到一条直线，是所有样本导致线上的欧式距离之和最小。
最小二乘“参数估计 (parameter estimation)”:求解w和b使得下式最小化的过程。
E(w,b)是关于w和b的凸函数，当关于w和b的导数均为零时得到w和b的最优解。U型曲线的函数通常是凸函数。对于实数集上的函数，凹凸性可通过求解二阶导数进行判断：当二阶导数在区间上≥0，则是凸函数；若二阶导数在区间上恒>0，则称为严格凸函数。
令公式(3.5), (3.6)为零，得到w和b最优解的闭式解(closed-form solution):
3.2.2 多元线性回归 (multivariate linear regression)：for regresion
, 使得 
.
此时，对应于一元线性回归模型的E(w,b),有
对
求导，并令求导结果为零，得到最优解的闭式解：
当
为满秩矩阵 (full-rank matrix) 或正定矩阵(positive definite matrix)时，令式 (3.10)为零，可得到：
现实任务中，往往不是满秩矩阵，即任务中存在大量的变量，其数目超过样例数，导致X的列数多于行数，此时，可以求得的多个解，均能使 MSE 最小化。
此时，选择哪一个作为最优解，通常由学习算法的归纳偏好 (inductive bias)决定，常见做法是引入正则化 (regularization).
令模型预测值逼近y的衍生物：假设我们认为示例所对应的输出标记是在 指数尺度上变化，则 可将输出标记的对数作为线性回归拟合的目标，称为“对数线性回归 (log-linear regression)”,如下：
实际上等价于 
，此时，虽然表面上看，这仍是线性回归，但实质上 是在求解输入空间到输出空间的非线性映射，如下图所示：
3.3 对数几率回归：for classification
从回归到分类：找到一个单调可微函数，将分类任务的真实标记y 与 线性回归模型的预测值联系起来，也就是说，找到一个函数，可以将实数值 转换为 0/1 值。
从单位阶跃函数 (unit-step function) 到 对数几率函数 (logistic function):
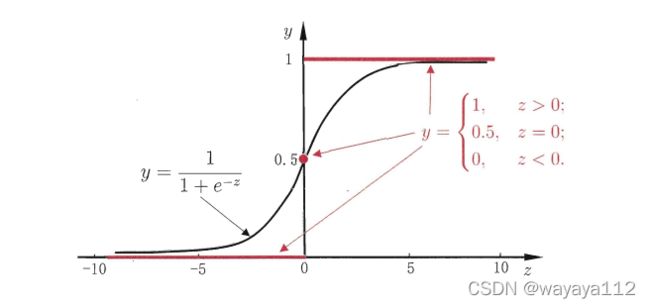红色为unit-step function；黑色为logistic function
对数几率函数是一种“Sigmoid函数”，将实数值z转换为一个接近0或1的y值，且在z=0附近变化很大。当作为分类任务的目标函数时，在进行反向传播进行求偏导时，z=0附近可能出现梯度消失。
对
两边同时取log，得到
，实质上是 让线性回归的预测结果逼近真是标记的对数几率 (logit).
将y是为样本x作为正例的可能性，则1-y是其作为反例的可能性。
称为 “几率 (odds)”,反映了 x作为正例的相对可能性。而取log后称为“对数几率 (log odds==logit)”，即
虽然名字是“回归”，但实际上是一种分类学习方法。其优点有：
1. 直接对分类可能性建模，不需要事先假设数据分布，避免了假设分布不准确带来的问题；
2. 不是仅仅预测出“类别”，而是 给出了近似概率。
3. logistic function是任意阶可导的凸函数，易于求导得到最优解
重写式 (3.19)后，得到
使用极大似然估计 (Maximum likelihood method)来估计w和b。对数似然为：
即令每个样本属于其真实标记的概率越大越好。将3.25 带入3.26中，且最大化3.25等价于最小化以下负对数似然：
![l\left ( w,b \right )=- \sum_{i=1}^{m}[\left ( y_{i}ln \ p\left ( y_{i}|x_{i;w,b} \right )+ \left ( 1-y_{i} \right ) ln\ \left ( 1- \ p\left ( y_{i}|x_{i;w,b} \right )\right )\right )]](http://img.e-com-net.com/image/info8/3438aa2dafba4b8abbe69c25d9b4f784.gif)
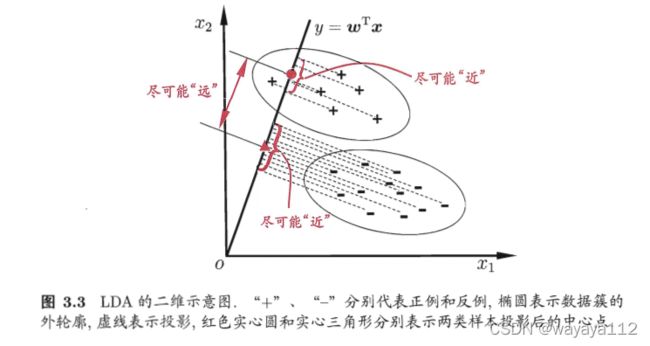
3.4 线性判别分析 (Linear Discriminant Analysis)
在二分类问题上，亦称为“Fisher判别分析”。
training时，给定训练样例集，设法将样例投影到一条直线上，以使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离；test时，给定新样本，将其投影到该条直线上，根据投影点位置，确定新样本类别。如下为二维示意图：
给定数据集
, 令
分别表示第
类示例的集合、均值向量、协方差矩阵。
将数据投影到直线w上时，两类样本的中心在直线上的投影分别为 
(均为实数)
当将所有样本点都投影到直线上时，此时两类样本的协方差分别为 
(均为实数)
让同类样例投影点的协方差尽可能小，以使同类样例的投影点尽可能接近，即 令
尽可能小
让类中心之间的距离尽可能大，以使 异类样例的投影点尽可能远离，即令 
尽可能大。同时考虑两者，则得到以下LDA最大化目标:
类内散度矩阵 (within-class scatter matrix):
类间散度矩阵 (between-class scatter matrix):
如何确定w？
令上述LDA 最大化目标J 的分母为1，则等价于
使用拉格朗日乘子，上式(3.36)等价于