（笔记）ROC & AUC 总结

Section 1：ROC曲线

ROC曲线也称为接受者操作特征曲线（Receiver Operating Characteristic）或感受性曲线，ROC曲线上的每个点反映着对同一信号刺激的感受性，主要是用于X对Y的预测准确率情况。

ROC 曲线图是反映敏感性与特异性之间关系的曲线。

X轴：负正类率(false postive rate，FPR)特异度，划分实例中所有负例占所有负例的比例；(1-Specificity)

Y轴：真正类率(true postive rate，TPR)灵敏度，Sensitivity(正类覆盖率)（又是召回率recall）

根据曲线位置，把整个图划分成了两部分，曲线下方部分的面积被称为 AUC（Area Under Curve），用来表示预测准确性，AUC 值越高，也就是曲线下方面积越大，说明预测准确率越高。曲线越接近左上角（X 越小，Y 越大），预测准确率越高。

针对一个二分类问题，会将实例分成正类（Positive）或者负类（Negative）。

但是实际中分类时，会出现四种情况（都是针对预测的类别来命名的）：

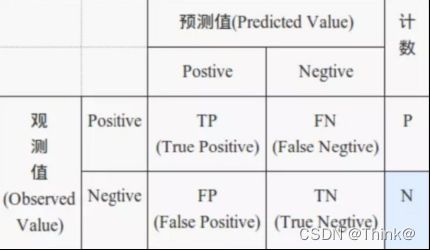
(1)真正类(True Postive，TP)（预测为正类，实际是正类）

(2)假负类(False Negative，FN)（预测为负类，实际是正类）

(3)假正类(False Postive，FP)（预测为正类，实际是负类）

(4)真负类(True Negative，TN)（预测为负类，实际是负类）

由上表可得出横，纵轴的计算公式：

(1)真正类率(True Postive Rate)TPR: TP/(TP+FN),代表分类器预测的正类中实际正实例占所有正实例的比例。Sensitivity

(2)负正类率(False Postive Rate)FPR: FP/(FP+TN)，代表分类器预测的正类中实际负实例占所有负实例的比例。1-Specificity

(3)真负类率(True Negative Rate)TNR: TN/(FP+TN),代表分类器预测的负类中实际负实例占所有负实例的比例，TNR=1-FPR。Specificity

ROC曲线的应用场景有很多，根据上述的定义，其最直观的应用就是能反映模型在选取不同阈值的时候其敏感性（sensitivity, FPR）和其精确性（specificity, TPR）的趋势走向。不过，相比于其他的P-R曲线（精确度和召回率），ROC曲线有一个巨大的优势就是，当正负样本的分布发生变化时，其形状能够基本保持不变，而P-R曲线的形状一般会发生剧烈的变化，因此该评估指标能降低不同测试集带来的干扰，更加客观的衡量模型本身的性能。

混淆矩阵：

ROC 曲线其实是多个混淆矩阵的结果组合。

以疾病检测为例，以下是一个有监督的二分类模型，模型对每个样本的预测结果为一个概率值，我们需要从中选取一个阈值来判断健康与否。定好一个阈值之后，超过此阈值定义为不健康，低于此阈值定义为健康，就可以得出混淆矩阵。

而如果在上述模型中我们没有定好阈值，而是将模型预测结果从高到低排序，将每个结果的概率值依次作为阈值，那么就可以得到多个混淆矩阵。对于每个混淆矩阵，我们计算两个指标 TPR 和FPR, 以 FPR 为 x 轴，TPR 为 y 轴画图，就得到了 ROC 曲线。

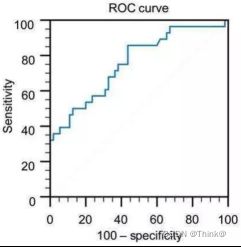
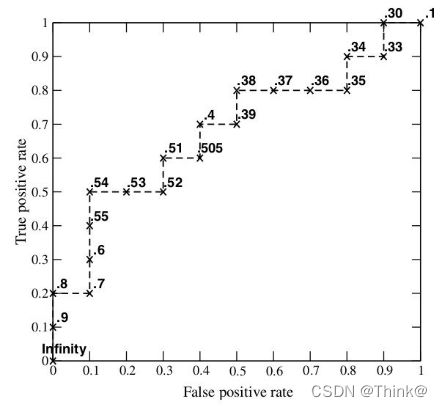
假设采用Logistic回归分类器，其给出针对每个实例为正类的概率，那么通过设定一个阈值如0.6，概率大于等于0.6的为正类，小于0.6的为负类。对应的就可以算出一组(FPR,TPR),在平面中得到对应坐标点。随着阈值的逐渐减小，越来越多的实例被划分为正类，但是这些正类中同样也掺杂着真正的负实例，即TPR和FPR会同时增大。阈值最大时，对应坐标点为(0,0),阈值最小时，对应坐标点(1,1)。

图中实线为ROC曲线，线上每个点对应着一个阈值。

横轴FPR:1-TNR,1-Specificity，FPR越大，预测正类中实际负类越多。

纵轴TPR：Sensitivity(正类覆盖率),TPR越大，预测正类中实际正类越多。

理想目标：TPR=1，FPR=0,即图中(0,1)点，故ROC曲线越靠拢(0,1)点，越偏离45度对角线越好，Sensitivity、Specificity越大效果越好

Link：

https://zhuanlan.zhihu.com/p/53015815

Section 2：绘制ROC曲线

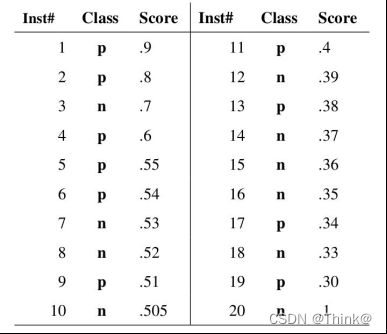
Step 1：按照属于“正样本”的概率将所有样本排序。

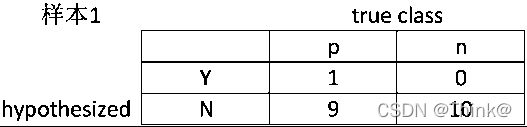
Step 2：依次来看每个样本，对于样本1，如果使用样本1的score值做阈值，即只有score大于等于0.9时，样本才能归类到真阳性（true positive），这样在ROC曲线图中，样本1对应的混淆矩阵（confusion matrix）为

 

其中，只有样本1被看作是正确分类了（也就是我们预测是正样本，实际也是正样本）；其余还有9个实际是正样本，而预测是负样本的（2，4，5，6，9，11，13，17，19）；剩下的实际是负样本，都预测出是负样本（也就是false positive = 0， true negative = 10）。

从混淆矩阵中，我们可以算出X轴坐标（false positive rate）= 0/（0+10）= 0 和Y轴坐标（true positive rate）= 1/（1+9）= 0.1，这就是下图中的第一个点。

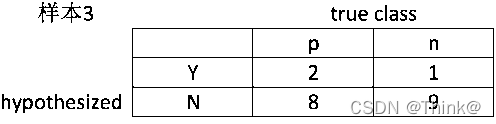
同理来看样本3，样本3的混淆矩阵为：

其中，样本1，2被看作是正确分类（也就是预测是正样本，实际也是正样本）；其余还有8个实际是正样本，而预测是负样本的（2，4，5，6，9，11，13，17，19）；而样本3是假阳性（预测是正样本，实际是负样本）；剩下的（7，8，10，12，14，15，16，18，20）实际是负样本，都预测出是负样本（也就是false positive = 1， true negative = 9）。

从样本3的混淆矩阵中，可以算出X轴坐标（false positive rate）= 1/（1+9）= 0.1 和Y轴坐标（true positive rate）= 2/（2+8）= 0.2，这就是上图中的第三个点。

依次把20个样本的混淆矩阵列出来，再算出X轴坐标（false positive rate） 和Y轴坐标（true positive rate），就可以得到ROC曲线。

Link：

https://www.zhihu.com/question/22844912/answer/246037337

Section 3：AUC值

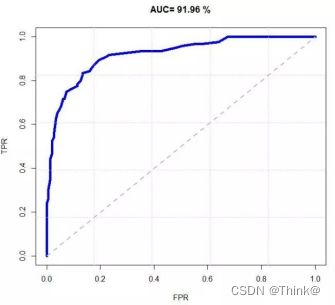
AUC (Area under Curve)：ROC 曲线下的面积，取值范围一般在 0.1 到 1 之间，很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而AUC作为数值可以直观的评价分类器的好坏，对应AUC值更大的分类器效果更好。

AUC 的常用计算方法有：

1. 梯形法则：早期由于测试样本有限，我们得到的 AUC 曲线呈阶梯状。曲线上的每个点向 X 轴做垂线，得到若干梯形，这些梯形面积之和也就是 AUC。
2. Mann-Whitney 统计量： 统计正负样本对中，有多少个组中的正样本的概率大于负样本的概率。这种估计随着样本规模的扩大而逐渐逼近真实值。

AUC的用途

从 AUC 判断分类器（预测模型）优劣的标准：AUC 值越大的分类器，正确率越高。

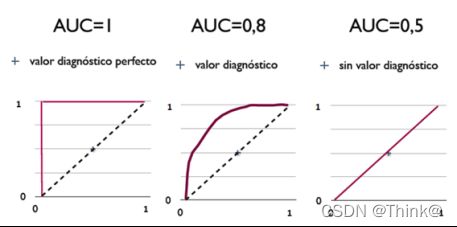
• AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。但在绝大多数预测的场合，不存在完美分类器。
• 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
• AUC = 0.5，跟随机猜测一样（例：抛硬币），模型没有预测价值。
• AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

不同模型的比较

总的来说，AUC 值越大，模型的分类效果越好，模型的检测结果越准确。不过两个模型AUC值相等并不代表模型效果相同，例子如下：

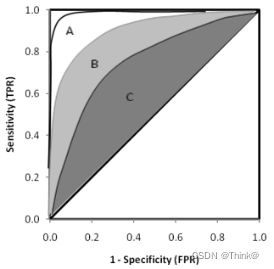
下图中有三条 ROC 曲线，A 模型比 B 和 C 都要好。

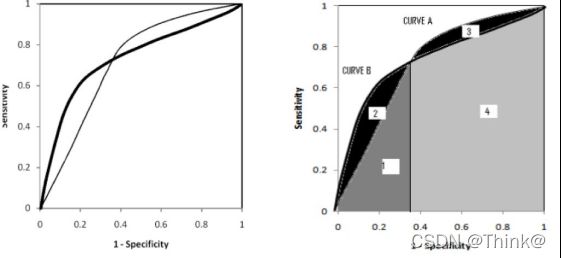
下面两幅图中两条 ROC 曲线相交于一点，AUC 值几乎一样：当需要高 Sensitivity 时，模型 A比 B 好；当需要高 Speciticity 时，模型 B 比A好；

最优临界点

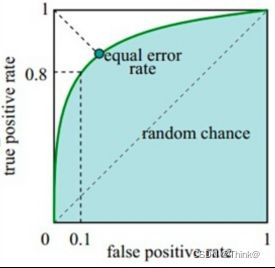
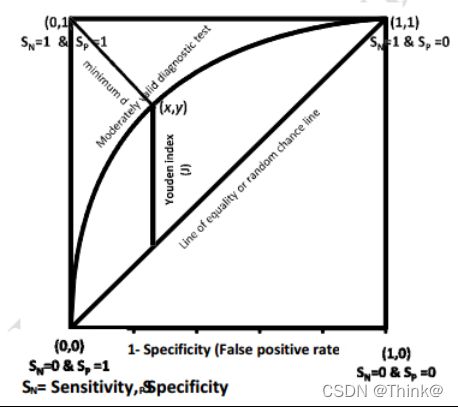
所谓找到最优临界点，就是保证TPR高的同时FPR要尽量的小，建立 max（TPR+（1-FPR））的模型。有两种方法：找到离（0,1）最近的点和Youden index。

1. 令 Sn 和 Sp 分别对应于 sensitivity 和 specificity，所有 ROC 曲线上的点到 ROC 的距离可以表示为d，让 d 最小的点即为最优临界点；

2. Youden index : 最大化 ROC 曲线上的点到 x 轴的垂直距离（最大化 TPR (Sn) 和 FPR (1-Sp) 的差异）；

性能比较-Delong test

ROC曲线的性能可以通过曲线下面积即 AUC来得到，可以使用Delong test来通过统计学的角度比较两个 ROC 曲线，可以得到两个曲线的 P 值，P < 0.05可以看作两个曲线有较大差异。

Link：

https://zhuanlan.zhihu.com/p/152197756