岳轩子

深度学习前馈神经网络（2）自动梯度计算和优化问题

这篇接上一篇
深度学习第3章前馈神经网络实验五 pytorch实现

4.3 自动梯度计算和预定义算子
- 4.3.1 利用预定义算子重新实现前馈神经网络
- 4.3.2 完善Runner类
- 4.3.3 模型训练
- 4.3.4 性能评价
4.4 优化问题
- 4.4.1 参数初始化
- 4.4.2 梯度消失问题
- - 4.4.2.1 模型构建
  - 4.4.2.2 使用Sigmoid型函数进行训练
- 4.4.3 死亡 ReLU 问题
- - 4.4.3.1 使用ReLU进行模型训练
  - 4.4.3.2 使用Leaky ReLU进行模型训练
习题
- 1. 使用pytorch的预定义算子来重新实现二分类任务。
- 2. 增加一个3个神经元的隐藏层，再次实现二分类，并与1做对比。
- 3.【思考题】自定义梯度计算和自动梯度计算：从计算性能、计算结果等多方面比较，谈谈自己的看法。
需要导入的包
补充
- 1. torch.optim.SGD()
- 2. torch.nn.init
- 3. 梯度消失和梯度爆炸产生的原因即解决办法
总结
参考

4.3 自动梯度计算和预定义算子

虽然我们能够通过模块化的方式比较好地对神经网络进行组装，但是每个模块的梯度计算过程仍然十分繁琐且容易出错。在深度学习框架中，已经封装了自动梯度计算的功能，我们只需要聚焦模型架构，不再需要耗费精力进行计算梯度。

pytorch提供了nn.Module类，来方便快速的实现自己的层和模型。模型和层都可以基于nn.Module扩充实现，模型只是一种特殊的层。

继承了nn.Module类的算子中，可以在内部直接调用其它继承nn.Module类的算子，pytorch框架会自动识别算子中内嵌的nn.Module类算子，并自动计算它们的梯度，并在优化时更新它们的参数。

torch.nn.Module在pytorch中的相应内容是什么？请简要介绍。

torch.nn.Module是所有神经网络模块的基类，所有的神经网络模型都应该继承这个基类，即pytorch 里面一切自定义操作基本上都是继承nn.Module类来实现的，并进行重载_init_ (初始化)和 forward(前向传播)函数。即在_init_ 进行模型子模块的构建，在forward进行子模块的拼接。每个类都有一个对应的nn.funcational函数，类定义了所需要的arguments和模块的parameters ,在forward函数中将arguments和parameters传给nn.funcational的对应的函数来实现forward功能。

注意事项：

一般把网络中具有可学习参数的层（如全连接层、卷积层等）（模块类的初始化）放在构造函数__init__()中
forward方法是必须要重写的，它是实现模型的功能，实现各个层之间的连接关系的核心

4.3.1 利用预定义算子重新实现前馈神经网络

下面我们使用Pytorch的预定义算子来重新实现二分类任务。
主要使用到的预定义算子为torch.nn.Linear

CLASS torch.nn.Linear(in_features, out_features, bias=True, device=None, dtype=None)

torch.nn.Linear算子可以接受一个形状为 $H_{in}]$ 的输入张量，其中 $" * "$ 表示张量中可以有任意的其它额外维度，并计算它与形状为 $out\_features, in\_features]$ 的权重矩阵的乘积，然后生成形状为 $H_{out}]$ 的输出张量。 torch.nn.Linear算子默认有偏置参数，可以通过bias=False设置不带偏置。代码实现如下：

import torch.nn as nn
import torch.nn.functional as F
from torch.nn.init import constant_, normal_, uniform_
 
 
class Model_MLP_L2_V2(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Model_MLP_L2_V2, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        normal_(self.fc1.weight, mean=0., std=1.)
        constant_(self.fc1.bias, val=0.0)
        self.fc2 = nn.Linear(hidden_size, output_size)
        normal_(self.fc2.weight, mean=0., std=1.)
        constant_(self.fc2.bias, val=0.0)
        self.act_fn = torch.sigmoid
 
    # 前向计算
    def forward(self, inputs):
        z1 = self.fc1(inputs)
        a1 = self.act_fn(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn(z2)
        return a2

4.3.2 完善Runner类

基于上一节实现的 RunnerV2_1 类，本节的 RunnerV2_2类在训练过程中使用自动梯度计算；模型保存时，使用state_dict方法获取模型参数；模型加载时，使用set_state_dict方法加载模型参数.

import torch
 
class RunnerV2_2(object):
    def __init__(self, model, optimizer, metric, loss_fn, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric
 
        # 记录训练过程中的评估指标变化情况
        self.train_scores = []
        self.dev_scores = []
 
        # 记录训练过程中的评价指标变化情况
        self.train_loss = []
        self.dev_loss = []
 
    def train(self, train_set, dev_set, **kwargs):
        # 将模型切换为训练模式
        self.model.train()
 
        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_epochs = kwargs.get("log_epochs", 100)
        # 传入模型保存路径，如果没有传入值则默认为"best_model.pdparams"
        save_path = kwargs.get("save_path", "best_model.pdparams")
 
        # log打印函数，如果没有传入则默认为"None"
        custom_print_log = kwargs.get("custom_print_log", None)
 
        # 记录全局最优指标
        best_score = 0
        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            X, y = train_set
            # 获取模型预测
            logits = self.model(X)
            # 计算交叉熵损失
            trn_loss = self.loss_fn(logits, y)
            self.train_loss.append(trn_loss.item())
            # 计算评估指标
            trn_score = self.metric(logits, y).item()
            self.train_scores.append(trn_score)
 
            # 自动计算参数梯度
            trn_loss.backward()
            if custom_print_log is not None:
                # 打印每一层的梯度
                custom_print_log(self)
 
            # 参数更新
            self.optimizer.step()
            # 清空梯度
            self.optimizer.zero_grad()
 
            dev_score, dev_loss = self.evaluate(dev_set)
            # 如果当前指标为最优指标，保存该模型
            if dev_score > best_score:
                self.save_model(save_path)
                print(f"[Evaluate] best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
                best_score = dev_score
 
            if log_epochs and epoch % log_epochs == 0:
                print(f"[Train] epoch: {epoch}/{num_epochs}, loss: {trn_loss.item()}")
 
    # 模型评估阶段，使用'torch.no_grad()'控制不计算和存储梯度
    @torch.no_grad()
    def evaluate(self, data_set):
        # 将模型切换为评估模式
        self.model.eval()
 
        X, y = data_set
        # 计算模型输出
        logits = self.model(X)
        # 计算损失函数
        loss = self.loss_fn(logits, y).item()
        self.dev_loss.append(loss)
        # 计算评估指标
        score = self.metric(logits, y).item()
        self.dev_scores.append(score)
        return score, loss
 
    def predict(self, X):
        # 将模型切换为评估模式
        self.model.eval()
        return self.model(X)
 
    # 使用'model.state_dict()'获取模型参数，并进行保存
    def save_model(self, saved_path):
        torch.save(self.model.state_dict(), saved_path)
 
    # 使用'model.set_state_dict'加载模型参数
    def load_model(self, model_path):
        state_dict = torch.load(model_path)
        self.model.set_state_dict(state_dict)

4.3.3 模型训练

实例化RunnerV2类，并传入训练配置，代码实现如下：

from metric import accuracy
 
# 设置模型
input_size = 2
hidden_size = 5
output_size = 1
model = Model_MLP_L2_V2(input_size=input_size, hidden_size=hidden_size, output_size=output_size)
 
# 设置损失函数
loss_fn = F.binary_cross_entropy
 
# 设置优化器
learning_rate = 0.2
optimizer = torch.optim.SGD(model.parameters(), learning_rate)
 
# 设置评价指标
metric = accuracy
 
# 其他参数
epoch_num = 1000
saved_path = 'best_model.pdparams'
 
# 实例化RunnerV2类，并传入训练配置
runner = RunnerV2_2(model, optimizer, metric, loss_fn)
runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=epoch_num, log_epochs=50, save_path="best_model.pdparams")

运行结果：

[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.50000
[Train] epoch: 0/1000, loss: 0.8091480135917664
[Evaluate] best accuracy performence has been updated: 0.50000 --> 0.51250
[Evaluate] best accuracy performence has been updated: 0.51250 --> 0.52500
[Evaluate] best accuracy performence has been updated: 0.52500 --> 0.54375
[Evaluate] best accuracy performence has been updated: 0.54375 --> 0.59375
[Evaluate] best accuracy performence has been updated: 0.59375 --> 0.60000
[Evaluate] best accuracy performence has been updated: 0.60000 --> 0.62500
[Evaluate] best accuracy performence has been updated: 0.62500 --> 0.65625
[Evaluate] best accuracy performence has been updated: 0.65625 --> 0.69375
[Evaluate] best accuracy performence has been updated: 0.69375 --> 0.70625
[Evaluate] best accuracy performence has been updated: 0.70625 --> 0.71250
[Evaluate] best accuracy performence has been updated: 0.71250 --> 0.72500
[Evaluate] best accuracy performence has been updated: 0.72500 --> 0.73750
[Train] epoch: 50/1000, loss: 0.5222678184509277
[Evaluate] best accuracy performence has been updated: 0.73750 --> 0.74375
[Train] epoch: 100/1000, loss: 0.48690247535705566
[Evaluate] best accuracy performence has been updated: 0.74375 --> 0.75000
[Evaluate] best accuracy performence has been updated: 0.75000 --> 0.75625
[Train] epoch: 150/1000, loss: 0.4598698616027832
[Train] epoch: 200/1000, loss: 0.4409264028072357
[Evaluate] best accuracy performence has been updated: 0.75625 --> 0.76250
[Evaluate] best accuracy performence has been updated: 0.76250 --> 0.76875
[Train] epoch: 250/1000, loss: 0.4285047650337219
[Evaluate] best accuracy performence has been updated: 0.76875 --> 0.77500
[Train] epoch: 300/1000, loss: 0.4206601083278656
[Train] epoch: 350/1000, loss: 0.4157894551753998
[Train] epoch: 400/1000, loss: 0.41277965903282166
[Train] epoch: 450/1000, loss: 0.4109122157096863
[Train] epoch: 500/1000, loss: 0.4097384512424469
[Train] epoch: 550/1000, loss: 0.4089827537536621
[Train] epoch: 600/1000, loss: 0.4084780216217041
[Train] epoch: 650/1000, loss: 0.40812379121780396
[Train] epoch: 700/1000, loss: 0.4078601896762848
[Train] epoch: 750/1000, loss: 0.4076516032218933
[Train] epoch: 800/1000, loss: 0.40747684240341187
[Train] epoch: 850/1000, loss: 0.40732353925704956
[Train] epoch: 900/1000, loss: 0.40718430280685425
[Train] epoch: 950/1000, loss: 0.4070546627044678

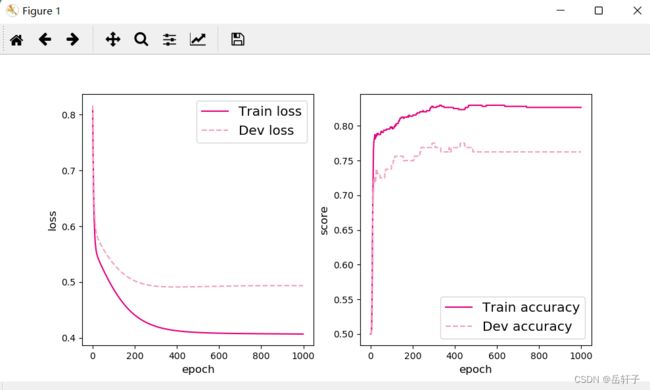
将训练过程中训练集与验证集的准确率变化情况进行可视化。

import matplotlib.pyplot as plt
# 可视化观察训练集与验证集的指标变化情况
def plot(runner, fig_name):
    plt.figure(figsize=(10,5))
    epochs = [i for i in range(len(runner.train_scores))]

    plt.subplot(1,2,1)
    plt.plot(epochs, runner.train_loss, color='#e4007f', label="Train loss")
    plt.plot(epochs, runner.dev_loss, color='#f19ec2', linestyle='--', label="Dev loss")
    # 绘制坐标轴和图例
    plt.ylabel("loss", fontsize='large')
    plt.xlabel("epoch", fontsize='large')
    plt.legend(loc='upper right', fontsize='x-large')

    plt.subplot(1,2,2)
    plt.plot(epochs, runner.train_scores, color='#e4007f', label="Train accuracy")
    plt.plot(epochs, runner.dev_scores, color='#f19ec2', linestyle='--', label="Dev accuracy")
    # 绘制坐标轴和图例
    plt.ylabel("score", fontsize='large')
    plt.xlabel("epoch", fontsize='large')
    plt.legend(loc='lower right', fontsize='x-large')
    
    plt.savefig(fig_name)
    plt.show()

plot(runner, 'fw-acc.pdf')

运行结果：

4.3.4 性能评价

使用测试数据对训练完成后的最优模型进行评价，观察模型在测试集上的准确率以及loss情况。代码如下：

# 模型评价
torch.load("best_model.pdparams")
score, loss = runner.evaluate([X_test, y_test])
print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))

运行结果：

[Test] score/loss: 0.7950/0.4897

在上述问题的基础上：增加一个3个神经元的隐藏层，再次实现二分类，并与其做对比。

import torch.nn as nn
import torch.nn.functional as F
from torch.nn.init import constant_, normal_, uniform_
import torch
from metric import accuracy
import matplotlib.pyplot as plt
from dataset import make_moons
 
# 采样1000个样本
n_samples = 1000
X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0.5)
num_train = 640
num_dev = 160
num_test = 200
X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]
y_train = y_train.reshape([-1, 1])
y_dev = y_dev.reshape([-1, 1])
y_test = y_test.reshape([-1, 1])
 
 
class Model_MLP_L2_V4(nn.Module):
    def __init__(self, input_size, hidden_size, hidden_size_3, output_size):
        super(Model_MLP_L2_V4, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        normal_(self.fc1.weight, mean=0., std=1.)
        constant_(self.fc1.bias, val=0.0)
        self.fc2 = nn.Linear(hidden_size, hidden_size_3)
        normal_(self.fc2.weight, mean=0., std=1.)
        constant_(self.fc2.bias, val=0.0)
        self.fc3 = nn.Linear(hidden_size_3, output_size)
        normal_(self.fc3.weight, mean=0., std=1.)
        constant_(self.fc3.bias, val=0.0)
        self.act_fn = torch.sigmoid
 
    # 前向计算
    def forward(self, inputs):
        z1 = self.fc1(inputs.to(torch.float32))
        a1 = self.act_fn(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn(z2)
        z3 = self.fc3(a2)
        a3 = self.act_fn(z3)
        return a3
 
 
class RunnerV2_2(object):
    def __init__(self, model, optimizer, metric, loss_fn, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric
 
        # 记录训练过程中的评估指标变化情况
        self.train_scores = []
        self.dev_scores = []
 
        # 记录训练过程中的评价指标变化情况
        self.train_loss = []
        self.dev_loss = []
 
    def train(self, train_set, dev_set, **kwargs):
        # 将模型切换为训练模式
        self.model.train()
 
        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_epochs = kwargs.get("log_epochs", 100)
        # 传入模型保存路径，如果没有传入值则默认为"best_model.pdparams"
        save_path = kwargs.get("save_path", "best_model.pdparams")
 
        # log打印函数，如果没有传入则默认为"None"
        custom_print_log = kwargs.get("custom_print_log", None)
 
        # 记录全局最优指标
        best_score = 0
        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            X, y = train_set
            # 获取模型预测
            logits = self.model(X)
            # 计算交叉熵损失
            trn_loss = self.loss_fn(logits, y)
            self.train_loss.append(trn_loss.item())
            # 计算评估指标
            trn_score = self.metric(logits, y).item()
            self.train_scores.append(trn_score)
 
            # 自动计算参数梯度
            trn_loss.backward()
            if custom_print_log is not None:
                # 打印每一层的梯度
                custom_print_log(self)
 
            # 参数更新
            self.optimizer.step()
            # 清空梯度
            self.optimizer.zero_grad()
 
            dev_score, dev_loss = self.evaluate(dev_set)
            # 如果当前指标为最优指标，保存该模型
            if dev_score > best_score:
                self.save_model(save_path)
                print(f"[Evaluate] best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
                best_score = dev_score
 
            if log_epochs and epoch % log_epochs == 0:
                print(f"[Train] epoch: {epoch}/{num_epochs}, loss: {trn_loss.item()}")
 
    # 模型评估阶段，使用'torch.no_grad()'控制不计算和存储梯度
    @torch.no_grad()
    def evaluate(self, data_set):
        # 将模型切换为评估模式
        self.model.eval()
 
        X, y = data_set
        # 计算模型输出
        logits = self.model(X)
        # 计算损失函数
        loss = self.loss_fn(logits, y).item()
        self.dev_loss.append(loss)
        # 计算评估指标
        score = self.metric(logits, y).item()
        self.dev_scores.append(score)
        return score, loss
 
    def predict(self, X):
        # 将模型切换为评估模式
        self.model.eval()
        return self.model(X)
 
    # 使用'model.state_dict()'获取模型参数，并进行保存
    def save_model(self, saved_path):
        torch.save(self.model.state_dict(), saved_path)
 
    # 使用'model.set_state_dict'加载模型参数
    def load_model(self, model_path):
        state_dict = torch.load(model_path)
        self.model.set_state_dict(state_dict)
 
 
# 设置模型
input_size = 2
hidden_size = 5
hidden_size_3 = 3
output_size = 1
model = Model_MLP_L2_V4(input_size=input_size, hidden_size=hidden_size, hidden_size_3=3, output_size=output_size)
 
# 设置损失函数
loss_fn = F.binary_cross_entropy
 
# 设置优化器
learning_rate = 0.2
optimizer = torch.optim.SGD(model.parameters(), learning_rate)
 
# 设置评价指标
metric = accuracy
 
# 其他参数
epoch_num = 1000
saved_path = 'best_model.pdparams'
 
# 实例化RunnerV2类，并传入训练配置
runner = RunnerV2_2(model, optimizer, metric, loss_fn)
runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=epoch_num, log_epochs=50, save_path="best_model.pdparams")
 
 
# 可视化观察训练集与验证集的指标变化情况
def plot(runner, fig_name):
    plt.figure(figsize=(10, 5))
    epochs = [i for i in range(len(runner.train_scores))]
 
    plt.subplot(1, 2, 1)
    plt.plot(epochs, runner.train_loss, color='#e4007f', label="Train loss")
    plt.plot(epochs, runner.dev_loss, color='#f19ec2', linestyle='--', label="Dev loss")
    # 绘制坐标轴和图例
    plt.ylabel("loss", fontsize='large')
    plt.xlabel("epoch", fontsize='large')
    plt.legend(loc='upper right', fontsize='x-large')
 
    plt.subplot(1, 2, 2)
    plt.plot(epochs, runner.train_scores, color='#e4007f', label="Train accuracy")
    plt.plot(epochs, runner.dev_scores, color='#f19ec2', linestyle='--', label="Dev accuracy")
    # 绘制坐标轴和图例
    plt.ylabel("score", fontsize='large')
    plt.xlabel("epoch", fontsize='large')
    plt.legend(loc='lower right', fontsize='x-large')
 
    plt.savefig(fig_name)
    plt.show()
 
 
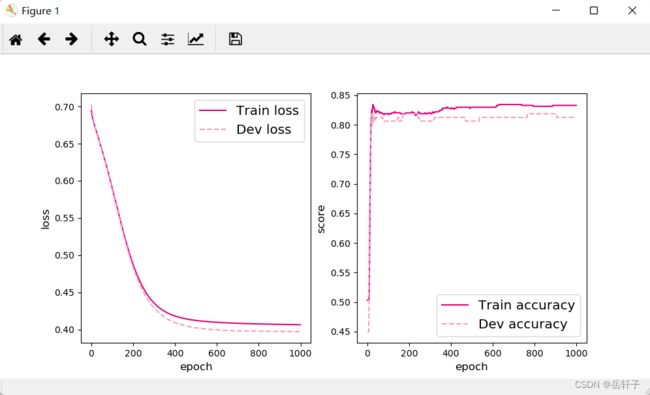
plot(runner, 'fw-acc.pdf')
 
# 模型评价
torch.load("best_model.pdparams")
score, loss = runner.evaluate([X_test, y_test])
print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))

运行结果：

outer_circ_x.shape: torch.Size([500]) outer_circ_y.shape: torch.Size([500])
outer_circ_x.shape: torch.Size([500]) inner_circ_y.shape: torch.Size([500])
after concat shape: torch.Size([1000])
X shape: torch.Size([1000, 2])
y shape: torch.Size([1000])
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.45000
[Train] epoch: 0/1000, loss: 0.6945466995239258
[Evaluate] best accuracy performence has been updated: 0.45000 --> 0.48750
[Evaluate] best accuracy performence has been updated: 0.48750 --> 0.54375
[Evaluate] best accuracy performence has been updated: 0.54375 --> 0.59375
[Evaluate] best accuracy performence has been updated: 0.59375 --> 0.63750
[Evaluate] best accuracy performence has been updated: 0.63750 --> 0.66250
[Evaluate] best accuracy performence has been updated: 0.66250 --> 0.69375
[Evaluate] best accuracy performence has been updated: 0.69375 --> 0.73125
[Evaluate] best accuracy performence has been updated: 0.73125 --> 0.75000
[Evaluate] best accuracy performence has been updated: 0.75000 --> 0.76875
[Evaluate] best accuracy performence has been updated: 0.76875 --> 0.78125
[Evaluate] best accuracy performence has been updated: 0.78125 --> 0.80000
[Evaluate] best accuracy performence has been updated: 0.80000 --> 0.81250
[Evaluate] best accuracy performence has been updated: 0.81250 --> 0.81875
[Train] epoch: 50/1000, loss: 0.6421956419944763
[Train] epoch: 100/1000, loss: 0.5900207757949829
[Train] epoch: 150/1000, loss: 0.5342556238174438
[Train] epoch: 200/1000, loss: 0.4871096611022949
[Train] epoch: 250/1000, loss: 0.45485734939575195
[Train] epoch: 300/1000, loss: 0.43542352318763733
[Train] epoch: 350/1000, loss: 0.4243297576904297
[Train] epoch: 400/1000, loss: 0.4180295467376709
[Train] epoch: 450/1000, loss: 0.41435056924819946
[Train] epoch: 500/1000, loss: 0.41209086775779724
[Train] epoch: 550/1000, loss: 0.4106135964393616
[Train] epoch: 600/1000, loss: 0.40958476066589355
[Train] epoch: 650/1000, loss: 0.40882715582847595
[Train] epoch: 700/1000, loss: 0.4082435965538025
[Train] epoch: 750/1000, loss: 0.40777772665023804
[Train] epoch: 800/1000, loss: 0.4073949456214905
[Train] epoch: 850/1000, loss: 0.4070724546909332
[Train] epoch: 900/1000, loss: 0.4067947268486023
[Train] epoch: 950/1000, loss: 0.4065505862236023
[Test] score/loss: 0.8150/0.4290

通过对比，我们发现增加隐藏层，可以提高准确率

4.4 优化问题

在本节中，我们通过实践来发现神经网络模型的优化问题，并思考如何改进。

4.4.1 参数初始化

实现一个神经网络前，需要先初始化模型参数。如果对每一层的权重和偏置都用0初始化，那么通过第一遍前向计算，所有隐藏层神经元的激活值都相同；在反向传播时，所有权重的更新也都相同，这样会导致隐藏层神经元没有差异性，出现对称权重现象。

接下来，将模型参数全都初始化为0，看实验结果。这里重新定义了一个类，两个线性层的参数全都初始化为0。

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.init import constant_, normal_, uniform_
 
 
class Model_MLP_L2_V4(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Model_MLP_L2_V4, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        constant_(self.fc1.weight, val=0.0)
        constant_(self.fc1.bias, val=0.0)
        self.fc2 = nn.Linear(hidden_size, output_size)
        constant_(self.fc2.weight, val=0.0)
        constant_(self.fc2.bias, val=0.0)
        self.act_fn = torch.sigmoid
 
    # 前向计算
    def forward(self, inputs):
        z1 = self.fc1(inputs)
        a1 = self.act_fn(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn(z2)
        return a2

def print_weights(runner):
    print('The weights of the Layers：')
    for item in runner.model.named_parameters():
        print(item)

利用Runner类训练模型：

# 设置模型
input_size = 2
hidden_size = 5
output_size = 1
model = Model_MLP_L2_V4(input_size=input_size, hidden_size=hidden_size, output_size=output_size)
 
# 设置损失函数
loss_fn = F.binary_cross_entropy
 
# 设置优化器
learning_rate = 0.2  # 5e-2
optimizer = torch.optim.SGD(model.parameters(), learning_rate)
 
# 设置评价指标
metric = accuracy
 
# 其他参数
epoch = 2000
saved_path = 'best_model.pdparams'
 
# 实例化RunnerV2类，并传入训练配置
runner = RunnerV2_2(model, optimizer, metric, loss_fn)
runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=5, log_epochs=50, save_path="best_model.pdparams", custom_print_log=print_weights)

运行结果：

The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[0., 0.],
        [0., 0.],
        [0., 0.],
        [0., 0.],
        [0., 0.]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([0., 0., 0., 0., 0.], requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[0., 0., 0., 0., 0.]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([0.], requires_grad=True))
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.50000
[Train] epoch: 0/5, loss: 0.6931472420692444
The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[0., 0.],
        [0., 0.],
        [0., 0.],
        [0., 0.],
        [0., 0.]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([0., 0., 0., 0., 0.], requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[0., 0., 0., 0., 0.]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([2.7940e-10], requires_grad=True))
The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[0., 0.],
        [0., 0.],
        [0., 0.],
        [0., 0.],
        [0., 0.]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([0., 0., 0., 0., 0.], requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[0., 0., 0., 0., 0.]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([5.5879e-10], requires_grad=True))
The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[0., 0.],
        [0., 0.],
        [0., 0.],
        [0., 0.],
        [0., 0.]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([0., 0., 0., 0., 0.], requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[0., 0., 0., 0., 0.]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([8.3819e-10], requires_grad=True))
The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[0., 0.],
        [0., 0.],
        [0., 0.],
        [0., 0.],
        [0., 0.]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([0., 0., 0., 0., 0.], requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[0., 0., 0., 0., 0.]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([1.1176e-09], requires_grad=True))

这里我把训练次数提升到5000，
运行结果：

# 这里只输出最后五次的结果
The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[-0.7841,  1.3522],
        [-0.7841,  1.3522],
        [-0.7841,  1.3522],
        [-0.7841,  1.3522],
        [-0.7841,  1.3522]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([-0.2695, -0.2695, -0.2695, -0.2695, -0.2695], requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[-1.6042, -1.6042, -1.6042, -1.6042, -1.6042]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([3.4718], requires_grad=True))
The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[-0.7841,  1.3522],
        [-0.7841,  1.3522],
        [-0.7841,  1.3522],
        [-0.7841,  1.3522],
        [-0.7841,  1.3522]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([-0.2695, -0.2695, -0.2695, -0.2695, -0.2695], requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[-1.6043, -1.6043, -1.6043, -1.6043, -1.6043]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([3.4719], requires_grad=True))
The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[-0.7840,  1.3521],
        [-0.7840,  1.3521],
        [-0.7840,  1.3521],
        [-0.7840,  1.3521],
        [-0.7840,  1.3521]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([-0.2695, -0.2695, -0.2695, -0.2695, -0.2695], requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[-1.6043, -1.6043, -1.6043, -1.6043, -1.6043]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([3.4721], requires_grad=True))
The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[-0.7840,  1.3521],
        [-0.7840,  1.3521],
        [-0.7840,  1.3521],
        [-0.7840,  1.3521],
        [-0.7840,  1.3521]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([-0.2695, -0.2695, -0.2695, -0.2695, -0.2695], requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[-1.6044, -1.6044, -1.6044, -1.6044, -1.6044]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([3.4722], requires_grad=True))
The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[-0.7840,  1.3520],
        [-0.7840,  1.3520],
        [-0.7840,  1.3520],
        [-0.7840,  1.3520],
        [-0.7840,  1.3520]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([-0.2695, -0.2695, -0.2695, -0.2695, -0.2695], requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[-1.6044, -1.6044, -1.6044, -1.6044, -1.6044]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([3.4723], requires_grad=True))

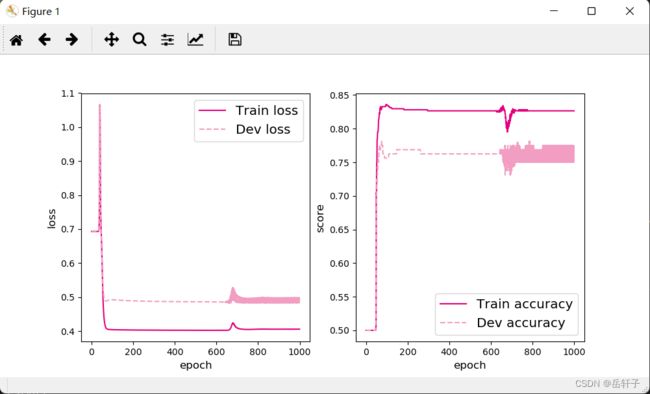
从输出结果看，前2000次训练，w的值一直是0，也可能改变了但是性能没有改变，这里我们分析一下：
这里的w一直在局部极小点徘徊，当到了2000左右，跳到了全局极小点，然后性能进行了提高！！！

我们可以提高学习率来加快 $w$ 的跳出

这里我把学习率改成5，训练轮数改为1000：
运行结果：

The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[-0.5812,  1.0367],
        [-0.5812,  1.0367],
        [-0.5812,  1.0367],
        [-0.5812,  1.0367],
        [-0.5812,  1.0367]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([-0.3856, -0.3856, -0.3856, -0.3856, -0.3856], requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[-2.0969, -2.0969, -2.0969, -2.0969, -2.0969]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([4.0437], requires_grad=True))
The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[-0.6149,  1.0128],
        [-0.6149,  1.0128],
        [-0.6149,  1.0128],
        [-0.6149,  1.0128],
        [-0.6149,  1.0128]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([-0.4510, -0.4510, -0.4510, -0.4510, -0.4510], requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[-2.0390, -2.0390, -2.0390, -2.0390, -2.0390]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([4.1869], requires_grad=True))
The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[-0.5812,  1.0367],
        [-0.5812,  1.0367],
        [-0.5812,  1.0367],
        [-0.5812,  1.0367],
        [-0.5812,  1.0367]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([-0.3856, -0.3856, -0.3856, -0.3856, -0.3856], requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[-2.0970, -2.0970, -2.0970, -2.0970, -2.0970]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([4.0437], requires_grad=True))
The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[-0.6149,  1.0128],
        [-0.6149,  1.0128],
        [-0.6149,  1.0128],
        [-0.6149,  1.0128],
        [-0.6149,  1.0128]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([-0.4510, -0.4510, -0.4510, -0.4510, -0.4510], requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[-2.0391, -2.0391, -2.0391, -2.0391, -2.0391]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([4.1868], requires_grad=True))
The weights of the Layers：
('fc1.weight', Parameter containing:
tensor([[-0.5812,  1.0367],
        [-0.5812,  1.0367],
        [-0.5812,  1.0367],
        [-0.5812,  1.0367],
        [-0.5812,  1.0367]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([-0.3857, -0.3857, -0.3857, -0.3857, -0.3857], requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[-2.0970, -2.0970, -2.0970, -2.0970, -2.0970]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([4.0437], requires_grad=True))

这里很快就跳出来了

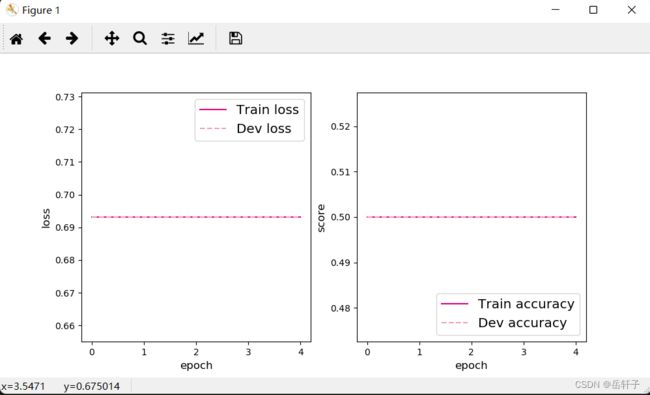
从输出结果看，二分类准确率为50%左右，说明模型没有学到任何内容。训练和验证loss几乎没有怎么下降。

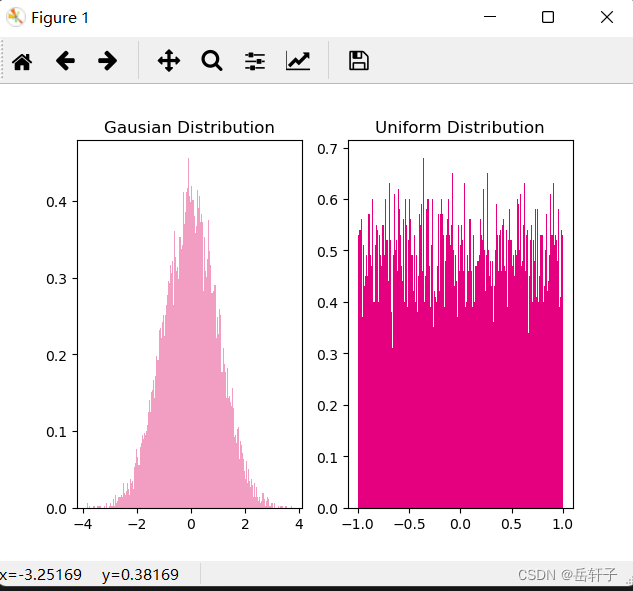
为了避免对称权重现象，可以使用高斯分布或均匀分布初始化神经网络的参数。

gausian_weights = torch.normal(mean=0.0, std=1.0, size=[10000])
uniform_weights = torch.Tensor(10000)
uniform_weights.uniform_(-1, 1)
# 绘制两种参数分布
plt.figure()
plt.subplot(1, 2, 1)
plt.title('Gausian Distribution')
plt.hist(gausian_weights, bins=200, density=True, color='#f19ec2')
plt.subplot(1, 2, 2)
plt.title('Uniform Distribution')
plt.hist(uniform_weights, bins=200, density=True, color='#e4007f')
plt.savefig('fw-gausian-uniform.pdf')
plt.show()

运行结果：

4.4.2 梯度消失问题

在神经网络的构建过程中，随着网络层数的增加，理论上网络的拟合能力也应该是越来越好的。但是随着网络变深，参数学习更加困难，容易出现梯度消失问题。

由于Sigmoid型函数的饱和性，饱和区的导数更接近于0，误差经过每一层传递都会不断衰减。当网络层数很深时，梯度就会不停衰减，甚至消失，使得整个网络很难训练，这就是所谓的梯度消失问题。
在深度神经网络中，减轻梯度消失问题的方法有很多种，一种简单有效的方式就是使用导数比较大的激活函数，如：ReLU。

下面通过一个简单的实验观察前馈神经网络的梯度消失现象和改进方法。

4.4.2.1 模型构建

定义一个前馈神经网络，包含4个隐藏层和1个输出层，通过传入的参数指定激活函数。代码实现如下：

a = torch.Tensor(10000)
 
 
class Model_MLP_L5(nn.Module):
    def __init__(self, input_size, output_size, act='sigmoid', w_init=normal_(a, mean=0.0, std=0.01), b_init=constant_(a, val=1.0)):
        super(Model_MLP_L5, self).__init__()
        self.fc1 = torch.nn.Linear(input_size, 3)
        self.fc2 = torch.nn.Linear(3, 3)
        self.fc3 = torch.nn.Linear(3, 3)
        self.fc4 = torch.nn.Linear(3, 3)
        self.fc5 = torch.nn.Linear(3, output_size)
        # 定义网络使用的激活函数
        if act == 'sigmoid':
            self.act = torch.sigmoid
        elif act == 'relu':
            self.act = F.relu
        elif act == 'lrelu':
            self.act = F.leaky_relu
        else:
            raise ValueError("Please enter sigmoid relu or lrelu!")
        # 初始化线性层权重和偏置参数
        self.init_weights(w_init, b_init)
 
    # 初始化线性层权重和偏置参数
    def init_weights(self, w_init, b_init):
        # 使用'named_sublayers'遍历所有网络层
        for n, m in self.named_parameters():
            # 如果是线性层，则使用指定方式进行参数初始化
            if isinstance(m, nn.Linear):
                w_init(m.weight)
                b_init(m.bias)
 
    def forward(self, inputs):
        outputs = self.fc1(inputs)
        outputs = self.act(outputs)
        outputs = self.fc2(outputs)
        outputs = self.act(outputs)
        outputs = self.fc3(outputs)
        outputs = self.act(outputs)
        outputs = self.fc4(outputs)
        outputs = self.act(outputs)
        outputs = self.fc5(outputs)
        outputs = torch.sigmoid(outputs)
        return outputs

4.4.2.2 使用Sigmoid型函数进行训练

使用Sigmoid型函数作为激活函数，为了便于观察梯度消失现象，只进行一轮网络优化。代码实现如下：

定义梯度打印函数

def print_grads(runner):
    # 打印每一层的权重的模
    print('The gradient of the Layers：')
    for name, item in runner.model.named_parameters():
        if len(item.size()) == 2:
             print(name, torch.norm(input=item, p=2))

# 学习率大小
lr = 0.01
# 定义网络，激活函数使用sigmoid
model = Model_MLP_L5(input_size=2, output_size=1, act='sigmoid')
# 定义优化器
optimizer = torch.optim.SGD(lr=lr, params=model.parameters())
# 定义损失函数，使用交叉熵损失函数
loss_fn = F.binary_cross_entropy
# 定义评价指标
metric = accuracy
# 指定梯度打印函数
custom_print_log=print_grads
# 实例化Runner类
runner = RunnerV2_2(model, optimizer, metric, loss_fn)
# 启动训练
runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=1, log_epochs=None, save_path="best_model.pdparams", custom_print_log=custom_print_log)

实例化RunnerV2_2类，并传入训练配置。代码实现如下：

# 实例化Runner类
runner = RunnerV2_2(model, optimizer, metric, loss_fn)

模型训练，打印网络每层梯度值的 $ℓ 2$ 范数。代码实现如下：

# 启动训练
runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=1, log_epochs=None, save_path="best_model.pdparams", custom_print_log=custom_print_log)

运行结果：

The gradient of the Layers：
fc1.weight tensor(1.0447, grad_fn=)
fc2.weight tensor(1.2803, grad_fn=)
fc3.weight tensor(0.8694, grad_fn=)
fc4.weight tensor(1.0071, grad_fn=)
fc5.weight tensor(0.5389, grad_fn=)
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.50000

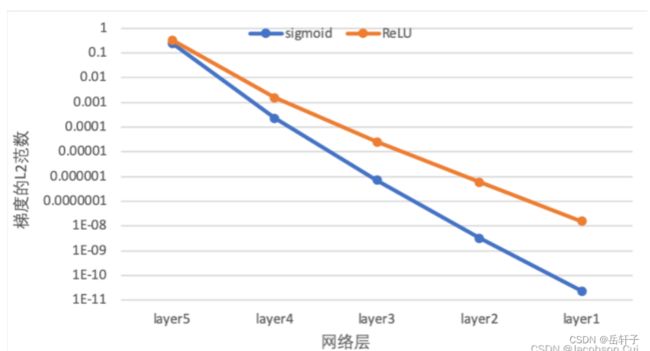
下图展示了使用不同激活函数时，网络每层梯度值的ℓ2范数情况。从结果可以看到，5层的全连接前馈神经网络使用Sigmoid型函数作为激活函数时，梯度经过每一个神经层的传递都会不断衰减，最终传递到第一个神经层时，梯度几乎完全消失。改为ReLU激活函数后，梯度消失现象得到了缓解，每一层的参数都具有梯度值。

4.4.3 死亡 ReLU 问题

ReLU激活函数可以一定程度上改善梯度消失问题，但是ReLU函数在某些情况下容易出现死亡 ReLU问题，使得网络难以训练。这是由于当x<0时，ReLU函数的输出恒为0。在训练过程中，如果参数在一次不恰当的更新后，某个ReLU神经元在所有训练数据上都不能被激活（即输出为0），那么这个神经元自身参数的梯度永远都会是0，在以后的训练过程中永远都不能被激活。而一种简单有效的优化方式就是将激活函数更换为Leaky ReLU、ELU等ReLU的变种。

4.4.3.1 使用ReLU进行模型训练

使用第4.4.2节中定义的多层全连接前馈网络进行实验，使用ReLU作为激活函数，观察死亡ReLU现象和优化方法。当神经层的偏置被初始化为一个相对于权重较大的负值时，可以想像，输入经过神经层的处理，最终的输出会为负值，从而导致死亡ReLU现象。

# 定义网络，并使用较大的负值来初始化偏置
model = Model_MLP_L5(input_size=2, output_size=1, act='relu', b_init=constant_(a, val=-8.0))

实例化RunnerV2类，启动模型训练，打印网络每层梯度值的 $ℓ 2$ 范数。代码实现如下：

# 实例化Runner类
runner = RunnerV2_2(model, optimizer, metric, loss_fn)
# 启动训练
runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=1, log_epochs=0, save_path="best_model.pdparams", custom_print_log=custom_print_log)

运行结果：

The gradient of the Layers：
fc1.weight tensor(0.8176, grad_fn=)
fc2.weight tensor(0.9802, grad_fn=)
fc3.weight tensor(0.9874, grad_fn=)
fc4.weight tensor(1.0451, grad_fn=)
fc5.weight tensor(0.4850, grad_fn=)
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.50000

从输出结果可以发现，使用 ReLU 作为激活函数，当满足条件时，会发生死亡ReLU问题，网络训练过程中 ReLU 神经元的梯度始终为0，参数无法更新。

针对死亡ReLU问题，一种简单有效的优化方式就是将激活函数更换为Leaky ReLU、ELU等ReLU 的变种。接下来，观察将激活函数更换为 Leaky ReLU时的梯度情况。

4.4.3.2 使用Leaky ReLU进行模型训练

将激活函数更换为Leaky ReLU进行模型训练，观察梯度情况。代码实现如下：

# 重新定义网络，使用Leaky ReLU激活函数
model = Model_MLP_L5(input_size=2, output_size=1, act='lrelu', b_init=constant_(a, val=-8.0))
 
# 实例化Runner类
runner = RunnerV2_2(model, optimizer, metric, loss_fn)
 
# 启动训练
runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=1, log_epochps=None, save_path="best_model.pdparams", custom_print_log=custom_print_log)

运行结果：

The gradient of the Layers：
fc1.weight tensor(0.7638, grad_fn=)
fc2.weight tensor(1.1522, grad_fn=)
fc3.weight tensor(1.0465, grad_fn=)
fc4.weight tensor(1.0655, grad_fn=)
fc5.weight tensor(0.5679, grad_fn=)
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.50000
[Train] epoch: 0/1, loss: 0.7000465989112854

从输出结果可以看到，将激活函数更换为Leaky ReLU后，死亡ReLU问题得到了改善，梯度恢复正常，参数也可以正常更新。但是由于 Leaky ReLU 中，x<0时的斜率默认只有0.01，所以反向传播时，随着网络层数的加深，梯度值越来越小。如果想要改善这一现象，将 Leaky ReLU 中，x<0时的斜率调大即可。

习题

1. 使用pytorch的预定义算子来重新实现二分类任务。

代码：

import torch.nn as nn
import torch.nn.functional as F
import os
import torch
from abc import abstractmethod
import math
import numpy as np


n_samples = 1000
X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0.15)

num_train = 640
num_dev = 160
num_test = 200

X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]

y_train = y_train.reshape([-1,1])
y_dev = y_dev.reshape([-1,1])
y_test = y_test.reshape([-1,1])

class Model_MLP_L2_V4(torch.nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(Model_MLP_L2_V4, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        w=torch.normal(0,0.1,size=(hidden_size,input_size),requires_grad=True)
        self.fc1.weight = nn.Parameter(w)

        self.fc2 = nn.Linear(hidden_size, output_size)
        w = torch.normal(0, 0.1, size=(output_size, hidden_size), requires_grad=True)
        self.fc2.weight = nn.Parameter(w)

        # 使用'torch.nn.functional.sigmoid'定义 Logistic 激活函数
        self.act_fn = torch.sigmoid

    # 前向计算
    def forward(self, inputs):
        z1 = self.fc1(inputs.to(torch.float32))
        a1 = self.act_fn(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn(z2)
        return a2


# def print_weights(runner):
#     print('The weights of the Layers：')
#
#     for item in runner.model.sublayers():
#         print(item.full_name()
#         for param in item.parameters():
#             print(param.numpy())


class RunnerV2_2(object):
    def __init__(self, model, optimizer, metric, loss_fn, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric

        # 记录训练过程中的评估指标变化情况
        self.train_scores = []
        self.dev_scores = []

        # 记录训练过程中的评价指标变化情况
        self.train_loss = []
        self.dev_loss = []

    def train(self, train_set, dev_set, **kwargs):
        # 将模型切换为训练模式
        self.model.train()

        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_epochs = kwargs.get("log_epochs", 100)
        # 传入模型保存路径，如果没有传入值则默认为"best_model.pdparams"
        save_path = kwargs.get("save_path", "best_model.pdparams")

        # log打印函数，如果没有传入则默认为"None"
        custom_print_log = kwargs.get("custom_print_log", None)

        # 记录全局最优指标
        best_score = 0
        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            X, y = train_set

            # 获取模型预测
            logits = self.model(X.to(torch.float32))
            # 计算交叉熵损失
            trn_loss = self.loss_fn(logits, y)
            self.train_loss.append(trn_loss.item())
            # 计算评估指标
            trn_score = self.metric(logits, y).item()
            self.train_scores.append(trn_score)

            # 自动计算参数梯度
            trn_loss.backward()
            if custom_print_log is not None:
                # 打印每一层的梯度
                custom_print_log(self)

            # 参数更新
            self.optimizer.step()
            # 清空梯度
            self.optimizer.zero_grad()   # reset gradient

            dev_score, dev_loss = self.evaluate(dev_set)
            # 如果当前指标为最优指标，保存该模型
            if dev_score > best_score:
                self.save_model(save_path)
                print(f"[Evaluate] best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
                best_score = dev_score

            if log_epochs and epoch % log_epochs == 0:
                print(f"[Train] epoch: {epoch}/{num_epochs}, loss: {trn_loss.item()}")
    @torch.no_grad()
    def evaluate(self, data_set):
        # 将模型切换为评估模式
        self.model.eval()

        X, y = data_set
        # 计算模型输出
        logits = self.model(X)
        # 计算损失函数
        loss = self.loss_fn(logits, y).item()
        self.dev_loss.append(loss)
        # 计算评估指标
        score = self.metric(logits, y).item()
        self.dev_scores.append(score)
        return score, loss

    # 模型测试阶段，使用'torch.no_grad()'控制不计算和存储梯度
    @torch.no_grad()
    def predict(self, X):
        # 将模型切换为评估模式
        self.model.eval()
        return self.model(X)

    # 使用'model.state_dict()'获取模型参数，并进行保存
    def save_model(self, saved_path):
        torch.save(self.model.state_dict(), saved_path)

    # 使用'model.set_state_dict'加载模型参数
    def load_model(self, model_path):
        state_dict = torch.load(model_path)
        self.model.load_state_dict(state_dict)


# 设置模型
input_size = 2
hidden_size = 5
output_size = 1
model = Model_MLP_L2_V4(input_size=input_size, hidden_size=hidden_size, output_size=output_size)

# 设置损失函数
loss_fn = F.binary_cross_entropy

# 设置优化器
learning_rate = 0.2 #5e-2
optimizer = torch.optim.SGD(model.parameters(),lr=learning_rate)

# 设置评价指标
metric = accuracy

# 其他参数
epoch = 2000
saved_path = 'best_model.pdparams'

# 实例化RunnerV2类，并传入训练配置
runner = RunnerV2_2(model, optimizer, metric, loss_fn)

runner.train([X_train, y_train], [X_dev, y_dev], num_epochs = epoch, log_epochs=50, save_path="best_model.pdparams")

plot(runner, 'fw-acc.pdf')

#模型评价
runner.load_model("best_model.pdparams")
score, loss = runner.evaluate([X_test, y_test])
print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))

这里补充几个函数：

make_moons函数代码：

import torch
# 新增make_moons函数
def make_moons(n_samples=1000, shuffle=True, noise=None):
    n_samples_out = n_samples // 2
    n_samples_in = n_samples - n_samples_out
    outer_circ_x = torch.cos(torch.linspace(0, math.pi, n_samples_out))
    outer_circ_y = torch.sin(torch.linspace(0, math.pi, n_samples_out))
    inner_circ_x = 1 - torch.cos(torch.linspace(0, math.pi, n_samples_in))
    inner_circ_y = 0.5 - torch.sin(torch.linspace(0, math.pi, n_samples_in))
    X = torch.stack(
        [torch.cat([outer_circ_x, inner_circ_x]),
         torch.cat([outer_circ_y, inner_circ_y])],
         axis=1
    )
    y = torch.cat(
        [torch.zeros([n_samples_out]), torch.ones([n_samples_in])]
    )
    if shuffle:
        idx = torch.randperm(X.shape[0])
        X = X[idx]
        y = y[idx]
    if noise is not None:
        X += np.random.normal(0.0, noise, X.shape)

    return X, y

accuracy函数代码：

def accuracy(preds, labels):
    # 判断是二分类任务还是多分类任务，preds.shape[1]=1时为二分类任务，preds.shape[1]>1时为多分类任务
    if preds.shape[1] == 1:
        preds=(preds>=0.5).to(torch.float32)

    else:
        preds = torch.argmax(preds,dim=1).int()

    return torch.mean((preds == labels).float())

plot函数代码：

import matplotlib.pyplot as plt
def plot(runner, fig_name):
    plt.figure(figsize=(10, 5))
    epochs = [i for i in range(len(runner.train_scores))]

    plt.subplot(1, 2, 1)
    plt.plot(epochs, runner.train_loss, color='#e4007f', label="Train loss")
    plt.plot(epochs, runner.dev_loss, color='#f19ec2', linestyle='--', label="Dev loss")
    # 绘制坐标轴和图例
    plt.ylabel("loss", fontsize='large')
    plt.xlabel("epoch", fontsize='large')
    plt.legend(loc='upper right', fontsize='x-large')

    plt.subplot(1, 2, 2)
    plt.plot(epochs, runner.train_scores, color='#e4007f', label="Train accuracy")
    plt.plot(epochs, runner.dev_scores, color='#f19ec2', linestyle='--', label="Dev accuracy")
    # 绘制坐标轴和图例
    plt.ylabel("score", fontsize='large')
    plt.xlabel("epoch", fontsize='large')
    plt.legend(loc='lower right', fontsize='x-large')
    plt.savefig(fig_name)
    plt.show()

运行结果：

[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.46250
[Train] epoch: 0/2000, loss: 0.7185732126235962
[Train] epoch: 50/2000, loss: 0.6900826096534729
[Evaluate] best accuracy performence has been updated: 0.46250 --> 0.46875
[Evaluate] best accuracy performence has been updated: 0.46875 --> 0.47500
[Evaluate] best accuracy performence has been updated: 0.47500 --> 0.49375
[Evaluate] best accuracy performence has been updated: 0.49375 --> 0.50625
[Evaluate] best accuracy performence has been updated: 0.50625 --> 0.52500
[Evaluate] best accuracy performence has been updated: 0.52500 --> 0.53125
[Train] epoch: 100/2000, loss: 0.6788896918296814
[Evaluate] best accuracy performence has been updated: 0.53125 --> 0.55000
[Evaluate] best accuracy performence has been updated: 0.55000 --> 0.55625
[Evaluate] best accuracy performence has been updated: 0.55625 --> 0.56250
[Evaluate] best accuracy performence has been updated: 0.56250 --> 0.56875
[Evaluate] best accuracy performence has been updated: 0.56875 --> 0.58125
[Evaluate] best accuracy performence has been updated: 0.58125 --> 0.59375
[Evaluate] best accuracy performence has been updated: 0.59375 --> 0.60625
[Evaluate] best accuracy performence has been updated: 0.60625 --> 0.61250
[Evaluate] best accuracy performence has been updated: 0.61250 --> 0.61875
[Evaluate] best accuracy performence has been updated: 0.61875 --> 0.63750
[Evaluate] best accuracy performence has been updated: 0.63750 --> 0.64375
[Evaluate] best accuracy performence has been updated: 0.64375 --> 0.65000
[Evaluate] best accuracy performence has been updated: 0.65000 --> 0.65625
[Evaluate] best accuracy performence has been updated: 0.65625 --> 0.66875
[Evaluate] best accuracy performence has been updated: 0.66875 --> 0.67500
[Evaluate] best accuracy performence has been updated: 0.67500 --> 0.68125
[Evaluate] best accuracy performence has been updated: 0.68125 --> 0.68750
[Evaluate] best accuracy performence has been updated: 0.68750 --> 0.69375
[Evaluate] best accuracy performence has been updated: 0.69375 --> 0.70000
[Evaluate] best accuracy performence has been updated: 0.70000 --> 0.70625
[Evaluate] best accuracy performence has been updated: 0.70625 --> 0.71250
[Evaluate] best accuracy performence has been updated: 0.71250 --> 0.72500
[Evaluate] best accuracy performence has been updated: 0.72500 --> 0.73125
[Evaluate] best accuracy performence has been updated: 0.73125 --> 0.73750
[Evaluate] best accuracy performence has been updated: 0.73750 --> 0.75000
[Evaluate] best accuracy performence has been updated: 0.75000 --> 0.75625
[Evaluate] best accuracy performence has been updated: 0.75625 --> 0.76875
[Evaluate] best accuracy performence has been updated: 0.76875 --> 0.78125
[Train] epoch: 150/2000, loss: 0.6434668898582458
[Train] epoch: 200/2000, loss: 0.5647386312484741
[Evaluate] best accuracy performence has been updated: 0.78125 --> 0.78750
[Train] epoch: 250/2000, loss: 0.4727853834629059
[Evaluate] best accuracy performence has been updated: 0.78750 --> 0.79375
[Evaluate] best accuracy performence has been updated: 0.79375 --> 0.80000
[Evaluate] best accuracy performence has been updated: 0.80000 --> 0.80625
[Train] epoch: 300/2000, loss: 0.40855950117111206
[Evaluate] best accuracy performence has been updated: 0.80625 --> 0.81250
[Evaluate] best accuracy performence has been updated: 0.81250 --> 0.81875
[Evaluate] best accuracy performence has been updated: 0.81875 --> 0.82500
[Evaluate] best accuracy performence has been updated: 0.82500 --> 0.83125
[Evaluate] best accuracy performence has been updated: 0.83125 --> 0.83750
[Evaluate] best accuracy performence has been updated: 0.83750 --> 0.85000
[Evaluate] best accuracy performence has been updated: 0.85000 --> 0.85625
[Train] epoch: 350/2000, loss: 0.36973756551742554
[Evaluate] best accuracy performence has been updated: 0.85625 --> 0.86250
[Evaluate] best accuracy performence has been updated: 0.86250 --> 0.86875
[Train] epoch: 400/2000, loss: 0.3448896110057831
[Train] epoch: 450/2000, loss: 0.3279474079608917
[Evaluate] best accuracy performence has been updated: 0.86875 --> 0.87500
[Evaluate] best accuracy performence has been updated: 0.87500 --> 0.88125
[Train] epoch: 500/2000, loss: 0.3161616027355194
[Evaluate] best accuracy performence has been updated: 0.88125 --> 0.88750
[Train] epoch: 550/2000, loss: 0.30801355838775635
[Train] epoch: 600/2000, loss: 0.3024461269378662
[Evaluate] best accuracy performence has been updated: 0.88750 --> 0.89375
[Train] epoch: 650/2000, loss: 0.2986697256565094
[Evaluate] best accuracy performence has been updated: 0.89375 --> 0.90000
[Train] epoch: 700/2000, loss: 0.2961108088493347
[Train] epoch: 750/2000, loss: 0.29436975717544556
[Evaluate] best accuracy performence has been updated: 0.90000 --> 0.90625
[Train] epoch: 800/2000, loss: 0.2931761145591736
[Train] epoch: 850/2000, loss: 0.2923488914966583
[Train] epoch: 900/2000, loss: 0.291767954826355
[Train] epoch: 950/2000, loss: 0.29135289788246155
[Train] epoch: 1000/2000, loss: 0.29105034470558167
[Train] epoch: 1050/2000, loss: 0.290824294090271
[Train] epoch: 1100/2000, loss: 0.29065054655075073
[Train] epoch: 1150/2000, loss: 0.2905128598213196
[Train] epoch: 1200/2000, loss: 0.29040008783340454
[Train] epoch: 1250/2000, loss: 0.29030489921569824
[Train] epoch: 1300/2000, loss: 0.2902221083641052
[Train] epoch: 1350/2000, loss: 0.29014816880226135
[Train] epoch: 1400/2000, loss: 0.290080726146698
[Train] epoch: 1450/2000, loss: 0.290018230676651
[Train] epoch: 1500/2000, loss: 0.2899594306945801
[Train] epoch: 1550/2000, loss: 0.28990358114242554
[Train] epoch: 1600/2000, loss: 0.2898501753807068
[Train] epoch: 1650/2000, loss: 0.2897987961769104
[Train] epoch: 1700/2000, loss: 0.2897491455078125
[Train] epoch: 1750/2000, loss: 0.28970101475715637
[Train] epoch: 1800/2000, loss: 0.2896542549133301
[Train] epoch: 1850/2000, loss: 0.28960874676704407
[Train] epoch: 1900/2000, loss: 0.28956443071365356
[Train] epoch: 1950/2000, loss: 0.28952115774154663
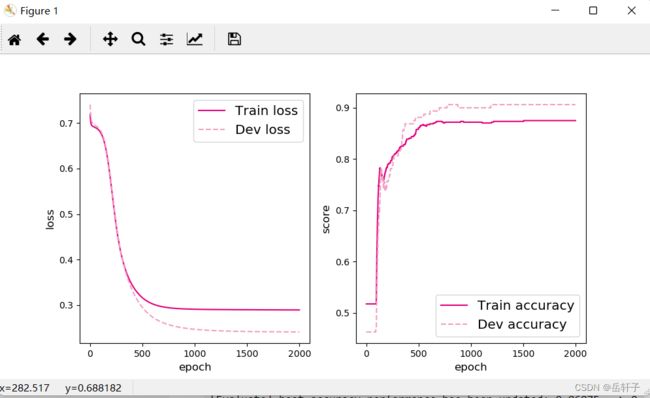
[Test] score/loss: 0.9050/0.2641

2. 增加一个3个神经元的隐藏层，再次实现二分类，并与1做对比。

改为3个神经元的隐藏层，我们需要增加一个隐藏层的参数
初始化：

input_size = 2
hidden_size = 5
# 增加
hidden_size2 = 3
output_size = 1
model = Model_MLP_L2_V4(input_size=input_size, hidden_size=hidden_size,hidden_size2=hidden_size2, output_size=output_size)

模型上要增加函数


class Model_MLP_L2_V4(torch.nn.Module):
    def __init__(self, input_size, hidden_size, hidden_size2, output_size):
        super(Model_MLP_L2_V4, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        w1=torch.normal(0,0.1,size=(hidden_size,input_size),requires_grad=True)
        self.fc1.weight = nn.Parameter(w1)

        self.fc2 = nn.Linear(hidden_size, hidden_size2)
        w2 = torch.normal(0, 0.1, size=(hidden_size2, hidden_size), requires_grad=True)
        self.fc2.weight = nn.Parameter(w2)

        self.fc3 = nn.Linear(hidden_size2, output_size)
        w3 = torch.normal(0, 0.1, size=(output_size, hidden_size2), requires_grad=True)
        self.fc3.weight = nn.Parameter(w3)

        # 使用'torch.nn.functional.sigmoid'定义 Logistic 激活函数
        self.act_fn = torch.sigmoid

    # 前向计算
    def forward(self, inputs):
        z1 = self.fc1(inputs.to(torch.float32))
        a1 = self.act_fn(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn(z2)
        z3 = self.fc3(a2)
        a3 = self.act_fn(z3)
        return a3

运行结果：

[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.51250
[Train] epoch: 0/2000, loss: 0.6943337321281433
[Train] epoch: 50/2000, loss: 0.6928403973579407
[Train] epoch: 100/2000, loss: 0.6928308606147766
[Train] epoch: 150/2000, loss: 0.6928211450576782
[Train] epoch: 200/2000, loss: 0.6928109526634216
[Train] epoch: 250/2000, loss: 0.6928002238273621
[Train] epoch: 300/2000, loss: 0.6927885413169861
[Train] epoch: 350/2000, loss: 0.692775547504425
[Train] epoch: 400/2000, loss: 0.6927613019943237
[Train] epoch: 450/2000, loss: 0.6927453875541687
[Train] epoch: 500/2000, loss: 0.6927274465560913
[Train] epoch: 550/2000, loss: 0.6927071213722229
[Train] epoch: 600/2000, loss: 0.6926836967468262
[Train] epoch: 650/2000, loss: 0.6926565170288086
[Train] epoch: 700/2000, loss: 0.6926250457763672
[Train] epoch: 750/2000, loss: 0.692588210105896
[Train] epoch: 800/2000, loss: 0.6925449371337891
[Train] epoch: 850/2000, loss: 0.6924934983253479
[Train] epoch: 900/2000, loss: 0.6924319267272949
[Train] epoch: 950/2000, loss: 0.6923579573631287
[Train] epoch: 1000/2000, loss: 0.6922681927680969
[Train] epoch: 1050/2000, loss: 0.6921581029891968
[Train] epoch: 1100/2000, loss: 0.6920220255851746
[Train] epoch: 1150/2000, loss: 0.691851794719696
[Train] epoch: 1200/2000, loss: 0.6916364431381226
[Train] epoch: 1250/2000, loss: 0.6913599967956543
[Train] epoch: 1300/2000, loss: 0.6909999847412109
[Train] epoch: 1350/2000, loss: 0.6905229687690735
[Train] epoch: 1400/2000, loss: 0.6898793578147888
[Train] epoch: 1450/2000, loss: 0.688992440700531
[Train] epoch: 1500/2000, loss: 0.6877409219741821
[Train] epoch: 1550/2000, loss: 0.6859274506568909
[Evaluate] best accuracy performence has been updated: 0.51250 --> 0.51875
[Evaluate] best accuracy performence has been updated: 0.51875 --> 0.52500
[Evaluate] best accuracy performence has been updated: 0.52500 --> 0.53750
[Evaluate] best accuracy performence has been updated: 0.53750 --> 0.54375
[Evaluate] best accuracy performence has been updated: 0.54375 --> 0.55625
[Evaluate] best accuracy performence has been updated: 0.55625 --> 0.56875
[Evaluate] best accuracy performence has been updated: 0.56875 --> 0.57500
[Evaluate] best accuracy performence has been updated: 0.57500 --> 0.59375
[Evaluate] best accuracy performence has been updated: 0.59375 --> 0.60000
[Evaluate] best accuracy performence has been updated: 0.60000 --> 0.60625
[Evaluate] best accuracy performence has been updated: 0.60625 --> 0.61875
[Evaluate] best accuracy performence has been updated: 0.61875 --> 0.62500
[Evaluate] best accuracy performence has been updated: 0.62500 --> 0.63125
[Evaluate] best accuracy performence has been updated: 0.63125 --> 0.63750
[Train] epoch: 1600/2000, loss: 0.6832197904586792
[Evaluate] best accuracy performence has been updated: 0.63750 --> 0.65000
[Evaluate] best accuracy performence has been updated: 0.65000 --> 0.65625
[Evaluate] best accuracy performence has been updated: 0.65625 --> 0.66875
[Evaluate] best accuracy performence has been updated: 0.66875 --> 0.68125
[Evaluate] best accuracy performence has been updated: 0.68125 --> 0.69375
[Evaluate] best accuracy performence has been updated: 0.69375 --> 0.70000
[Evaluate] best accuracy performence has been updated: 0.70000 --> 0.70625
[Evaluate] best accuracy performence has been updated: 0.70625 --> 0.71250
[Evaluate] best accuracy performence has been updated: 0.71250 --> 0.71875
[Evaluate] best accuracy performence has been updated: 0.71875 --> 0.72500
[Evaluate] best accuracy performence has been updated: 0.72500 --> 0.73125
[Evaluate] best accuracy performence has been updated: 0.73125 --> 0.73750
[Evaluate] best accuracy performence has been updated: 0.73750 --> 0.74375
[Evaluate] best accuracy performence has been updated: 0.74375 --> 0.75000
[Evaluate] best accuracy performence has been updated: 0.75000 --> 0.75625
[Evaluate] best accuracy performence has been updated: 0.75625 --> 0.76250
[Evaluate] best accuracy performence has been updated: 0.76250 --> 0.76875
[Evaluate] best accuracy performence has been updated: 0.76875 --> 0.77500
[Evaluate] best accuracy performence has been updated: 0.77500 --> 0.78125
[Evaluate] best accuracy performence has been updated: 0.78125 --> 0.79375
[Evaluate] best accuracy performence has been updated: 0.79375 --> 0.80000
[Evaluate] best accuracy performence has been updated: 0.80000 --> 0.80625
[Evaluate] best accuracy performence has been updated: 0.80625 --> 0.81250
[Train] epoch: 1650/2000, loss: 0.6790398955345154
[Evaluate] best accuracy performence has been updated: 0.81250 --> 0.81875
[Evaluate] best accuracy performence has been updated: 0.81875 --> 0.82500
[Evaluate] best accuracy performence has been updated: 0.82500 --> 0.83125
[Evaluate] best accuracy performence has been updated: 0.83125 --> 0.83750
[Evaluate] best accuracy performence has been updated: 0.83750 --> 0.84375
[Train] epoch: 1700/2000, loss: 0.6723501086235046
[Train] epoch: 1750/2000, loss: 0.661268413066864
[Train] epoch: 1800/2000, loss: 0.6425549387931824
[Train] epoch: 1850/2000, loss: 0.6118574142456055
[Train] epoch: 1900/2000, loss: 0.5674184560775757
[Train] epoch: 1950/2000, loss: 0.515984296798706
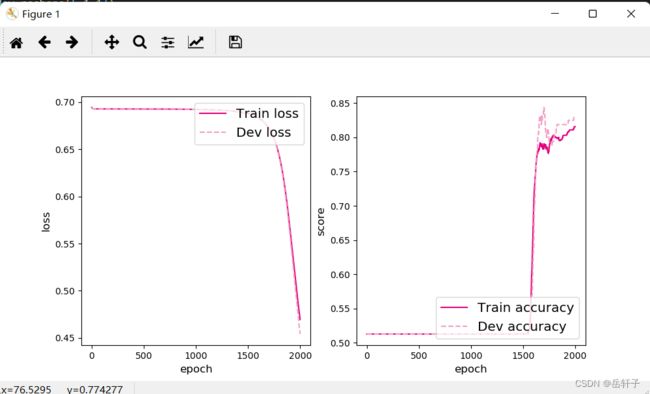
[Test] score/loss: 0.8100/0.6730

这里我们可以发现，训练模型在测试集上的准确率得到了进一步的提升。

3.【思考题】自定义梯度计算和自动梯度计算：从计算性能、计算结果等多方面比较，谈谈自己的看法。

使用前面实验Model_MLP_L2类

激活函数：

def backward(self, grads):
	outputs_grad_inputs = torch.multiply(self.outputs, (1.0 - self.outputs))
	return torch.multiply(grads, outputs_grad_inputs)

损失函数：

def backward(self):
	loss_grad_predicts = -1.0 * (self.labels / self.predicts - (1 - self.labels) / (1 - self.predicts)) / self.num
	self.model.backward(loss_grad_predicts)

自动梯度求导：

自定义梯度求导：

自定义梯度计算是一步到位，计算速度很快
对比了一下，发现二者更新的结果还是有很大出入的，不仅仅体现在测试集准确率上，这权重梯度也很不一样。
所以，在时间充裕爱好数学的方式下，尽量采用自定义求导。

需要导入的包

深度学习第3章线性分类实验四 pytorch实现 Softmax回归鸢尾花分类任务下篇

make_moons函数代码：

import torch
# 新增make_moons函数
def make_moons(n_samples=1000, shuffle=True, noise=None):
    n_samples_out = n_samples // 2
    n_samples_in = n_samples - n_samples_out
    outer_circ_x = torch.cos(torch.linspace(0, math.pi, n_samples_out))
    outer_circ_y = torch.sin(torch.linspace(0, math.pi, n_samples_out))
    inner_circ_x = 1 - torch.cos(torch.linspace(0, math.pi, n_samples_in))
    inner_circ_y = 0.5 - torch.sin(torch.linspace(0, math.pi, n_samples_in))
    X = torch.stack(
        [torch.cat([outer_circ_x, inner_circ_x]),
         torch.cat([outer_circ_y, inner_circ_y])],
         axis=1
    )
    y = torch.cat(
        [torch.zeros([n_samples_out]), torch.ones([n_samples_in])]
    )
    if shuffle:
        idx = torch.randperm(X.shape[0])
        X = X[idx]
        y = y[idx]
    if noise is not None:
        X += np.random.normal(0.0, noise, X.shape)

    return X, y

补充

1. torch.optim.SGD()

其中的SGD就是optim中的一个算法（优化器）：随机梯度下降算法

torch.optim是一个实现了各种优化算法的库。大部分常用的方法得到支持，并且接口具备足够的通用性，使得未来能够集成更加复杂的方法。

动手学深度学习-多层感知机中：updater = torch.optim.SGD(params, lr=lr)。其中的updater就是一个optimizer对象。

随机梯度下降（Stochastic gradient descent，SGD）是对批量梯度下降（Batch Gradient Descent）的改进，与批量梯度下降法相比，SGD每次更新时只随机取一个样本计算梯度，所以速度较快。但是，在频繁更新的情况下，会导致结果不稳定，波动较大，所以现在的SGD一般都指随机小批量梯度下降（Mini-Batch Gradient Descent），即随机抽取一批样本，以此更新参数。通常一小批数据含有的样本数量为50～256。

2. torch.nn.init

这里我们主要用来初始化一些参数，
比如：

方法	作用	参数
torch.nn.init.uniform(tensor, a=0, b=1)	从均匀分布U(a, b)中生成值，填充输入的张量或变量	* tensor - n维的torch.Tensor * a - 均匀分布的下界 * b - 均匀分布的上界
torch.nn.init.normal(tensor, mean=0, std=1)	从给定均值和标准差的正态分布N(mean, std)中生成值，填充输入的张量或变量	* tensor – n维的torch.Tensor * mean – 正态分布的均值 * std – 正态分布的标准差
torch.nn.init.constant(tensor, val)	用val的值填充输入的张量或变量	* tensor – n维的torch.Tensor或autograd.Variable * val – 用来填充张量的值

3. 梯度消失和梯度爆炸产生的原因即解决办法

首先解释一下什么是梯度消失和梯度爆炸

深度神经网络训练的时候，采用的是反向传播方式，该方式使用链式求导，计算每层梯度的时候会涉及一些连乘操作，因此如果网络过深。

那么如果连乘的因子大部分小于1，最后乘积的结果可能趋于0，也就是梯度消失，后面的网络层的参数不发生变化.

那么如果连乘的因子大部分大于1，最后乘积可能趋于无穷，这就是梯度爆炸。

梯度消失：（1）隐藏层的层数过多；（2）采用了不合适的激活函数(更容易产生梯度消失，但是也有可能产生梯度爆炸)
梯度爆炸：（1）隐藏层的层数过多；（2）权重的初始化值过大

解决：

梯度消失：

sigmoid容易发生，更换激活函数为 ReLU即可。

权重初始化用高斯初始化

梯度爆炸：

设置梯度剪切阈值，如果超过了该阈值，直接将梯度置为该值。

使用ReLU,maxout等替代sigmoid

总结

通过本次实验的内容,详细学习了torch.nn.Module的使用，以及自定义梯度计算和自动梯度计算之间的区别。
更加熟悉了paddle与pytorch之间的转换
知晓了在遇到前馈神经网络中参数为0的情况下，对结果数据结果的分析

参考

NNDL 实验4（上）
NNDL 实验五前馈神经网络（2）自动梯度计算 & 优化问题
torch.optim.SGD()
torch.nn.init

创作不易，如果对你有帮助，求求你给我个赞！！！
点赞 + 收藏 + 关注！！！
如有错误与建议，望告知！！！（将于下篇文章更正）
请多多关注我！！！谢谢！！！

你可能感兴趣的:(深度学习,python)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
理解Gunicorn：Python WSGI服务器的基石范范0825 ipython linux 运维
理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
Python数据分析与可视化实战指南 William数据分析 python python 数据
在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
python os.environ 江湖偌大 python 深度学习
os.environ['TF_CPP_MIN_LOG_LEVEL']='0'#默认值，输出所有信息os.environ['TF_CPP_MIN_LOG_LEVEL']='1'#屏蔽通知信息（INFO）os.environ['TF_CPP_MIN_LOG_LEVEL']='2'#屏蔽通知信息和警告信息（INFO\WARNING）os.environ['TF_CPP_MIN_LOG_LEVEL']='
Python中os.environ基本介绍及使用方法鹤冲天Pro #Python python 服务器开发语言
文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
Pyecharts数据可视化大屏：打造沉浸式数据分析体验我的运维人生信息可视化数据分析数据挖掘运维开发技术共享
Pyecharts数据可视化大屏：打造沉浸式数据分析体验在当今这个数据驱动的时代，如何将海量数据以直观、生动的方式展现出来，成为了数据分析师和企业决策者关注的焦点。Pyecharts，作为一款基于Python的开源数据可视化库，凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力，成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏，并通过实际代码案例
Python教程：一文了解使用Python处理XPath 旦莫 Python进阶 python 开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
python os.environ_python os.environ 读取和设置环境变量 weixin_39605414 python os.environ
>>>importos>>>os.environ.keys()['LC_NUMERIC','GOPATH','GOROOT','GOBIN','LESSOPEN','SSH_CLIENT','LOGNAME','USER','HOME','LC_PAPER','PATH','DISPLAY','LANG','TERM','SHELL','J2REDIR','LC_MONETARY','QT_QPA
将cmd中命令输出保存为txt文本文件落难Coder Windows cmd window
最近深度学习本地的训练中我们常常要在命令行中运行自己的代码，无可厚非，我们有必要保存我们的炼丹结果，但是复制命令行输出到txt是非常麻烦的，其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是：运行指令>输出到的文件名称或者具体保存路径测试下，我打开cmd并且ping一下百度：pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出：如果你再
使用Faiss进行高效相似度搜索 llzwxh888 faiss python
在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
python是什么意思中文-在python中%是什么意思编程大乐趣
Python中%有两种：1、数值运算：%代表取模，返回除法的余数。如：>>>7%212、%操作符（字符串格式化，stringformatting），说明如下：%[(name)][flags][width].[precision]typecode(name)为命名flags可以有+，-，''或0。+表示右对齐。-表示左对齐。''为一个空格，表示在正数的左侧填充一个空格，从而与负数对齐。0表示使用0填
Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Python python 开发语言大数据数据分析数据挖掘
大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
python八股文面试题分享及解析(1) Shawn________ python
#1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果：21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型，不仅仅改变
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
Python快速入门 —— 第三节：类与对象孤华暗香 Python快速入门 python 开发语言
第三节：类与对象目标：了解面向对象编程的基础概念，并学会如何定义类和创建对象。内容：类与对象：定义类：class关键字。类的构造函数：__init__()。类的属性和方法。对象的创建与使用。示例：classStudent:def__init__(self,name,age,major):self.name&#
pyecharts——绘制柱形图折线图 2224070247 信息可视化 python java 数据可视化
一、pyecharts概述自2013年6月百度EFE(ExcellentFrontEnd）数据可视化团队研发的ECharts1.0发布到GitHub网站以来，ECharts一直备受业界权威的关注并获得广泛好评，成为目前成熟且流行的数据可视化图表工具，被应用到诸多数据可视化的开发领域。Python作为数据分析领域最受欢迎的语言，也加入ECharts的使用行列，并研发出方便Python开发者使用的数据
Python 实现图片裁剪（附代码） | Python工具剑客阿良_ALiang
前言本文提供将图片按照自定义尺寸进行裁剪的工具方法，一如既往的实用主义。环境依赖ffmpeg环境安装，可以参考我的另一篇文章：windowsffmpeg安装部署_阿良的博客-CSDN博客本文主要使用到的不是ffmpeg，而是ffprobe也在上面这篇文章中的zip包中。ffmpy安装：pipinstallffmpy-ihttps://pypi.douban.com/simple代码不废话了，上代码
【华为OD技术面试真题 - 技术面】- python八股文真题题库（4) 算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例：文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片（Slicing）操作**基本切片语法
python os 环境变量 CV矿工 python 开发语言 numpy
环境变量：环境变量是程序和操作系统之间的通信方式。有些字符不宜明文写进代码里，比如数据库密码，个人账户密码，如果写进自己本机的环境变量里，程序用的时候通过os.environ.get（）取出来就行了。os.environ是一个环境变量的字典。环境变量的相关操作importos"""设置/修改环境变量：os.environ[‘环境变量名称’]=‘环境变量值’#其中key和value均为string类
Python爬虫解析工具之xpath使用详解 eqa11 python 爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中，数据提取是一个至关重要的环节。xpath作为一门
【华为OD技术面试真题 - 技术面】- python八股文真题题库（1）算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.数据预处理流程数据预处理的主要步骤工具和库2.介绍线性回归、逻辑回归模型线性回归（LinearRegression）模型形式：关键点：逻辑回归（LogisticRegression）模型形式：关键点：参数估计与评估：3.python浅拷贝及深拷贝浅拷贝（Shal
nosql数据库技术与应用知识点皆过客，揽星河 NoSQL nosql 数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
《Python数据分析实战终极指南》 xjt921122 python 数据分析开发语言
对于分析师来说，大家在学习Python数据分析的路上，多多少少都遇到过很多大坑**，有关于技能和思维的**：Excel已经没办法处理现有的数据量了，应该学Python吗？找了一大堆Python和Pandas的资料来学习，为什么自己动手就懵了？跟着比赛类公开数据分析案例练了很久，为什么当自己面对数据需求还是只会数据处理而没有分析思路？学了对比、细分、聚类分析，也会用PEST、波特五力这类分析法，为啥
Python中深拷贝与浅拷贝的区别 yuxiaoyu.
转自：http://blog.csdn.net/u014745194/article/details/70271868定义：在Python中对象的赋值其实就是对象的引用。当创建一个对象，把它赋值给另一个变量的时候，python并没有拷贝这个对象，只是拷贝了这个对象的引用而已。浅拷贝：拷贝了最外围的对象本身，内部的元素都只是拷贝了一个引用而已。也就是，把对象复制一遍，但是该对象中引用的其他对象我不复
Python开发常用的三方模块如下：换个网名有点难 python 开发语言
Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
Python编译器鹿鹿~ Python编译器 Python python 开发语言后端
嘿嘿嘿我又来了啊有些小盆友可能不知道Python其实是有编译器的，也就是PyCharm。你们可能会问到这个是干嘛的又不可以吃也不可以穿好像没有什么用，其实你还说对了这个还真的不可以吃也不可以穿，但是它用来干嘛的呢。用来编译你所打出的代码进行运行（可能这里说的有点不对但是只是个人认为）现在我们来说说PyCharm是用来干嘛的。PyCharm是一种PythonIDE，带有一整套可以帮助用户在使用Pyt
一文掌握python面向对象魔术方法（二）程序员neil python python 开发语言
接上篇：一文掌握python面向对象魔术方法（一）-CSDN博客目录六、迭代和序列化：1、__iter__(self):定义迭代器，使得类可以被for循环迭代。2、__getitem__(self,key):定义索引操作，如obj[key]。3、__setitem__(self,key,value):定义赋值操作，如obj[key]=value。4、__delitem__(self,key):定义
一文掌握python常用的list（列表）操作程序员neil python python 开发语言
目录一、创建列表1.直接创建列表：2.使用list()构造器3.使用列表推导式4.创建空列表二、访问列表元素1.列表支持通过索引访问元素，索引从0开始：2.还可以使用切片操作访问列表的一部分：三、修改列表元素四、添加元素1.append()：在末尾添加元素2.insert()：在指定位置插入元素五、删除元素1.del：删除指定位置的元素2.remove()：删除指定值的第一个匹配项3.pop()：
Python实现简单的机器学习算法 master_chenchengg python python 办公效率 python开发 IT
Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
python中的深拷贝与浅拷贝 anshejd70787 python
深拷贝和浅拷贝浅拷贝的时候，修改原来的对象，浅拷贝的对象不会发生改变。1、对象的赋值对象的赋值实际上是对象之间的引用：当创建一个对象，然后将这个对象赋值给另外一个变量的时候，python并没有拷贝这个对象，而只是拷贝了这个对象的引用。当对对象做赋值或者是参数传递或者作为返回值的时候，总是传递原始对象的引用，而不是一个副本。如下所示：>>>aList=["kel","abc",123]>>>bLis
Linux的Initrd机制被触发 linux
Linux 的 initrd 技术是一个非常普遍使用的机制，linux2.6 内核的 initrd 的文件格式由原来的文件系统镜像文件转变成了 cpio 格式，变化不仅反映在文件格式上， linux 内核对这两种格式的 initrd 的处理有着截然的不同。本文首先介绍了什么是 initrd 技术，然后分别介绍了 Linux2.4 内核和 2.6 内核的 initrd 的处理流程。最后通过对 Lin
maven本地仓库路径修改 bitcarter maven
默认maven本地仓库路径：C:\Users\Administrator\.m2 修改maven本地仓库路径方法： 1.打开E:\maven\apache-maven-2.2.1\conf\settings.xml 2.找到
XSD和XML中的命名空间 darrenzhu xml xsd schema namespace 命名空间
http://www.360doc.com/content/12/0418/10/9437165_204585479.shtml http://blog.csdn.net/wanghuan203/article/details/9203621 http://blog.csdn.net/wanghuan203/article/details/9204337 http://www.cn
Java 求素数运算周凡杨 java 算法素数
网络上对求素数之解数不胜数，我在此总结归纳一下，同时对一些编码，加以改进，效率有成倍热提高。第一种：原理: 6N(+-)1法任何一个自然数，总可以表示成为如下的形式之一： 6N，6N+1，6N+2，6N+3，6N+4，6N+5 (N=0，1，2，…)
java 单例模式 g21121 java
想必单例模式大家都不会陌生，有如下两种方式来实现单例模式： class Singleton { private static Singleton instance=new Singleton(); private Singleton(){} static Singleton getInstance() { return instance; }
Linux下Mysql源码安装 510888780 mysql
1.假设已经有mysql-5.6.23-linux-glibc2.5-x86_64.tar.gz (1)创建mysql的安装目录及数据库存放目录解压缩下载的源码包，目录结构，特殊指定的目录除外：
32位和64位操作系统墙头上一根草 32位和64位操作系统
32位和64位操作系统是指：CPU一次处理数据的能力是32位还是64位。现在市场上的CPU一般都是64位的，但是这些CPU并不是真正意义上的64 位CPU，里面依然保留了大部分32位的技术，只是进行了部分64位的改进。32位和64位的区别还涉及了内存的寻址方面，32位系统的最大寻址空间是2 的32次方= 4294967296（bit）= 4（GB）左右，而64位系统的最大寻址空间的寻址空间则达到了
我的spring学习笔记10-轻量级_Spring框架 aijuans Spring 3
一、问题提问： → 请简单介绍一下什么是轻量级？轻量级（Leightweight）是相对于一些重量级的容器来说的，比如Spring的核心是一个轻量级的容器，Spring的核心包在文件容量上只有不到1M大小，使用Spring核心包所需要的资源也是很少的，您甚至可以在小型设备中使用Spring。
mongodb 环境搭建及简单CURD antlove Web Install curd NoSQL mongo
一搭建mongodb环境 1. 在mongo官网下载mongodb 2. 在本地创建目录 "D:\Program Files\mongodb-win32-i386-2.6.4\data\db" 3. 运行mongodb服务 [mongod.exe --dbpath "D:\Program Files\mongodb-win32-i386-2.6.4\data\
数据字典和动态视图百合不是茶 oracle 数据字典动态视图系统和对象权限
数据字典（data dictionary）是 Oracle 数据库的一个重要组成部分，这是一组用于记录数据库信息的只读（read-only）表。随着数据库的启动而启动,数据库关闭时数据字典也关闭数据字典中包含数据库中所有方案对象（schema object）的定义(包括表，视图，索引，簇，同义词，序列，过程，函数，包，触发器等等) 数据库为一
多线程编程一般规则 bijian1013 java thread 多线程 java多线程
如果两个工两个以上的线程都修改一个对象，那么把执行修改的方法定义为被同步的，如果对象更新影响到只读方法，那么只读方法也要定义成同步的。不要滥用同步。如果在一个对象内的不同的方法访问的不是同一个数据，就不要将方法设置为synchronized的。
将文件或目录拷贝到另一个Linux系统的命令scp bijian1013 linux unix scp
一.功能说明 scp就是security copy，用于将文件或者目录从一个Linux系统拷贝到另一个Linux系统下。scp传输数据用的是SSH协议，保证了数据传输的安全，其格式如下： scp 远程用户名@IP地址：文件的绝对路径
【持久化框架MyBatis3五】MyBatis3一对多关联查询 bit1129 Mybatis3
以教员和课程为例介绍一对多关联关系，在这里认为一个教员可以叫多门课程，而一门课程只有1个教员教，这种关系在实际中不太常见，通过教员和课程是多对多的关系。示例数据：地址表： CREATE TABLE ADDRESSES ( ADDR_ID INT(11) NOT NULL AUTO_INCREMENT, STREET VAR
cookie状态判断引发的查找问题 bitcarter form cgi
先说一下我们的业务背景： 1.前台将图片和文本通过form表单提交到后台，图片我们都做了base64的编码，并且前台图片进行了压缩 2.form中action是一个cgi服务 3.后台cgi服务同时供PC，H5，APP 4.后台cgi中调用公共的cookie状态判断方法（公共的，大家都用，几年了没有问题）问题：（折腾两天。。。。） 1.PC端cgi服务正常调用，cookie判断没
通过Nginx,Tomcat访问日志(access log)记录请求耗时 ronin47
一、Nginx通过$upstream_response_time $request_time统计请求和后台服务响应时间 nginx.conf使用配置方式： log_format main '$remote_addr - $remote_user [$time_local] "$request" ''$status $body_bytes_sent "$http_r
java-67- n个骰子的点数。把n个骰子扔在地上，所有骰子朝上一面的点数之和为S。输入n，打印出S的所有可能的值出现的概率。 bylijinnan java
public class ProbabilityOfDice { /** * Q67 n个骰子的点数 * 把n个骰子扔在地上，所有骰子朝上一面的点数之和为S。输入n，打印出S的所有可能的值出现的概率。 * 在以下求解过程中，我们把骰子看作是有序的。 * 例如当n=2时，我们认为（1，2）和（2，1）是两种不同的情况 */ private stati
看别人的博客，觉得心情很好 Cb123456 博客心情
以为写博客，就是总结，就和日记一样吧，同时也在督促自己。今天看了好长时间博客: 职业规划: http://www.iteye.com/blogs/subjects/zhiyeguihua android学习: 1.http://byandby.i
[JWFD开源工作流]尝试用原生代码引擎实现循环反馈拓扑分析 comsci 工作流
我们已经不满足于仅仅跳跃一次，通过对引擎的升级，今天我测试了一下循环反馈模式，大概跑了200圈，引擎报一个溢出错误在一个流程图的结束节点中嵌入一段方程，每次引擎运行到这个节点的时候，通过实时编译器GM模块，计算这个方程，计算结果与预设值进行比较，符合条件则跳跃到开始节点，继续新一轮拓扑分析，直到遇到
JS常用的事件及方法 cwqcwqmax9 js
事件描述 onactivate 当对象设置为活动元素时触发。 onafterupdate 当成功更新数据源对象中的关联对象后在数据绑定对象上触发。 onbeforeactivate 对象要被设置为当前元素前立即触发。 onbeforecut 当选中区从文档中删除之前在源对象触发。 onbeforedeactivate 在 activeElement 从当前对象变为父文档其它对象之前立即
正则表达式验证日期格式 dashuaifu 正则表达式 IT其它 java其它
正则表达式验证日期格式 function isDate(d){ var v = d.match(/^(\d{4})-(\d{1,2})-(\d{1,2})$/i); if(!v) { this.focus(); return false; } } <input value="2000-8-8" onblu
Yii CModel.rules() 方法、validate预定义完整列表、以及说说验证 dcj3sjt126com yii
public array rules () {return} array 要调用 validate() 时应用的有效性规则。返回属性的有效性规则。声明验证规则，应重写此方法。每个规则是数组具有以下结构：array('attribute list', 'validator name', 'on'=>'scenario name', ...validation
UITextAttributeTextColor = deprecated in iOS 7.0 dcj3sjt126com ios
In this lesson we used the key "UITextAttributeTextColor" to change the color of the UINavigationBar appearance to white. This prompts a warning "first deprecated in iOS 7.0." Ins
判断一个数是质数的几种方法 EmmaZhao Math python
质数也叫素数，是只能被1和它本身整除的正整数，最小的质数是2，目前发现的最大的质数是p=2^57885161-1【注1】。判断一个数是质数的最简单的方法如下： def isPrime1(n): for i in range(2, n): if n % i == 0: return False return True 但是在上面的方法中有一些冗余的计算，所以
SpringSecurity工作原理小解读坏我一锅粥 SpringSecurity
SecurityContextPersistenceFilter ConcurrentSessionFilter WebAsyncManagerIntegrationFilter HeaderWriterFilter CsrfFilter LogoutFilter Use
JS实现自适应宽度的Tag切换 ini JavaScript html Web css html5
效果体验：http://hovertree.com/texiao/js/3.htm 该效果使用纯JavaScript代码，实现TAB页切换效果，TAB标签根据内容自适应宽度，点击TAB标签切换内容页。 HTML文件代码： <!DOCTYPE html> <html xmlns="http://www.w3.org/1999/xhtml"
Hbase Rest API : 数据查询 kane_xie REST hbase
hbase（hadoop）是用java编写的，有些语言（例如python）能够对它提供良好的支持，但也有很多语言使用起来并不是那么方便，比如c#只能通过thrift访问。Rest就能很好的解决这个问题。Hbase的org.apache.hadoop.hbase.rest包提供了rest接口，它内嵌了jetty作为servlet容器。启动命令：./bin/hbase rest s
JQuery实现鼠标拖动元素移动位置（源码+注释）明子健 jquery js 源码拖动鼠标
欢迎讨论指正！ print.html代码： <!DOCTYPE html> <html> <head> <meta http-equiv=Content-Type content="text/html;charset=utf-8"> <title>发票打印</title> &l
Postgresql 连表更新字段语法 update qifeifei PostgreSQL
下面这段sql本来目的是想更新条件下的数据，可是这段sql却更新了整个表的数据。sql如下： UPDATE tops_visa.visa_order SET op_audit_abort_pass_date = now() FROM tops_visa.visa_order as t1 INNER JOIN tops_visa.visa_visitor as t2 ON t1.
将redis,memcache结合使用的方案? tcrct redis cache
公司架构上使用了阿里云的服务，由于阿里的kvstore收费相当高，打算自建，自建后就需要自己维护，所以就有了一个想法，针对kvstore(redis)及ocs(memcache)的特点，想自己开发一个cache层，将需要用到list，set，map等redis方法的继续使用redis来完成，将整条记录放在memcache下，即findbyid，save等时就memcache，其它就对应使用redi
开发中遇到的诡异的bug wudixiaotie bug
今天我们服务器组遇到个问题：我们的服务是从Kafka里面取出数据，然后把offset存储到ssdb中，每个topic和partition都对应ssdb中不同的key，服务启动之后，每次kafka数据更新我们这边收到消息，然后存储之后就发现ssdb的值偶尔是-2,这就奇怪了，最开始我们是在代码中打印存储的日志，发现没什么问题，后来去查看ssdb的日志，才发现里面每次set的时候都会对同一个key

深度学习 前馈神经网络（2）自动梯度计算和优化问题

目录

4.3 自动梯度计算和预定义算子

4.3.1 利用预定义算子重新实现前馈神经网络

4.3.2 完善Runner类

4.3.3 模型训练

4.3.4 性能评价

4.4 优化问题

4.4.1 参数初始化

4.4.2 梯度消失问题

4.4.2.1 模型构建

4.4.2.2 使用Sigmoid型函数进行训练

4.4.3 死亡 ReLU 问题

4.4.3.1 使用ReLU进行模型训练

4.4.3.2 使用Leaky ReLU进行模型训练

习题

1. 使用pytorch的预定义算子来重新实现二分类任务。

2. 增加一个3个神经元的隐藏层，再次实现二分类，并与1做对比。

3.【思考题】自定义梯度计算和自动梯度计算：从计算性能、计算结果等多方面比较，谈谈自己的看法。

需要导入的包

补充

1. torch.optim.SGD()

2. torch.nn.init

3. 梯度消失和梯度爆炸产生的原因即解决办法

总结

参考

你可能感兴趣的:(深度学习,python)

深度学习前馈神经网络（2）自动梯度计算和优化问题