量子笔记:量子比特的表示
目录
0. 概要
1. 从集合到希尔伯特(Hilbert)空间
1.1 空间
1.2 度量空间
1.3 线性空间
1.4 赋范线性空间
1.5 巴拿赫(Banach)空间
1.6 内积空间
1.7 希尔伯特空间
2. 量子比特
2.1 叠加态、坍缩
2.2 在复希尔伯特空间中的表示
2.4 基底
2.5 标准基底,标准正交基
2.7 坐标
2.8 计算基底 computational basis
2.9 狄拉克符号
0. 概要
量子计算、量子信息、量子编程自学笔记系列。
用自己能看懂的方式来表述对于量子计算基础知识的理解。
不求体系完备和逻辑严谨、但求通俗易懂。或能顺便给路过的小伙伴一些参考和启发那是纯属巧合概不认账^-^。当然,这里仅限于轮廓的勾勒和要点的连接,对细节感兴趣的话还是要找正经的参考书。
本节介绍单个量子比特的定义,在复希尔伯特空间中的表示,以及狄拉克符号。
1. 从集合到希尔伯特(Hilbert)空间
集合:开辟鸿蒙。。。
1.1 空间
空间就是具有(数学)结构的集合。换句话说,给集合加上(数学)结构的约束就得到空间。
1.2 度量空间
集合 + 度量(距离)结构 ![]() 度量空间。
度量空间。
1.3 线性空间
集合 + 线性结构 ![]() 线性空间。
线性空间。
1.4 赋范线性空间
同时具有距离结构又具有线性结构的集合称为赋范线性空间。
1.5 巴拿赫(Banach)空间
赋范线性空间X在其范数诱导的距离下,作为度量空间是完备的,即X中的任一Cauchy列都在X中收敛,称X为完备赋范线性空间,又称Banach空间 。
1.6 内积空间
在线性空间X上定义内积(点积、数性积、数量积)即得到内积空间,或者说,定义了内积的线性空间称为内积空间。内积通常记为![]() ,由内积可以很自然诱导出对应的范数即
,由内积可以很自然诱导出对应的范数即![]() ,因此内积空间是赋范线性空间。
,因此内积空间是赋范线性空间。
在实线性空间上定义内积得到实内积空间,也称欧几里德空间。
在复线性空间上定义内积得到复内积空间,也称酉空间。
1.7 希尔伯特空间
若内积空间X在其内积诱导出的范数下完备,则称X是Hilbert空间。或者说,完备的内积空间称为Hilbert空间。
2. 量子比特
2.1 叠加态、坍缩
量子比特(QuBit)是量子信息的基本单位。
量子比特是类似于经典比特的量子版本。但是,经典比特的状态是确定性的,要么是0要么是1,不可能同时既为0又为1。与经典世界相类似的是,量子比特有两种基态(分别记为基态0和基态1),而量子比特则(永远)是处于两种基态的叠加态,在观测之前不可能确定性地知道量子比特究竟属于何种状态。
在观测发生时,量子比特将会变成两个基态之一,这一过程称为“坍缩”。坍缩过程是不可逆的,坍缩过程在数学上可以理解为通过投影变换将叠加态变成基态0或者基态1。
2.2 在复希尔伯特空间中的表示
量子比特的状态可以用复希尔伯特空间![]() 上的向量来表示。假设复希尔伯特空间
上的向量来表示。假设复希尔伯特空间![]() 上的一个标准正交基为{
上的一个标准正交基为{![]() },则量子比特的状态可以表示为:
},则量子比特的状态可以表示为:
![]()
其中,a和b为复数(![]() ),表示复概率幅度(probability amplitude),满足
),表示复概率幅度(probability amplitude),满足![]() ,
,![]() 分别表示该量子比特在被观测时坍缩到基态
分别表示该量子比特在被观测时坍缩到基态![]() 的概率。
的概率。
2.4 基底
向量空间(线性空间)的基底是指能够张成该向量空间的一组线性无关向量组。
一个向量空间可以有有无数多组基底,这些基底所包含的向量称为基向量,基底中所包含的基向量的个数称为向量空间的维数(如果是有限个,则是有限维向量空间;否则就是无限维向量空间)。因此,不同的基底中所包含的基向量的个数必然是相等的。
比如说,![]() 是2维线性空间,
是2维线性空间,![]() 也是2维线性空间。注意,
也是2维线性空间。注意,![]() 与
与![]() 在某种程度是等价的,但是又并不完全相同,毕竟
在某种程度是等价的,但是又并不完全相同,毕竟![]() 中的复数运算规则在
中的复数运算规则在![]() 中是没有体现的。
中是没有体现的。
2.5 标准基底,标准正交基
虽然如上所述,一个向量空间的基底有无穷多种可能,但是实际使用时当然应该选择容易进行处理方便计算的基底,比如说标准基底(也称标准正交基:orthonormal basis)。
标准正交基有两方面的要点:
(1)标准:标准在这里是指该基底中每个基向量的长度都为1
(2)正交:正交是指该基底中的每两个基向量是相互正交的
任何一个基底都可以通过比如说格拉姆-施密特正交化方法变换为对应的标准正交基。
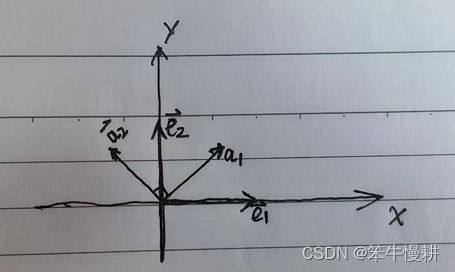
对于一个向量空间,标准正交基仍然不是唯一的,可以有无穷多个。如下图中所示,![]() 和
和![]() 都是
都是![]() 的标准正交基。容易想象,将
的标准正交基。容易想象,将![]() 旋转任意角度得到的向量组都是
旋转任意角度得到的向量组都是 ![]() 的标准正交基
的标准正交基
图1 ![]() 的标准正交基示意图
的标准正交基示意图
2.7 坐标
向量是一个抽象的概念。
有了基底后,就可以将向量以相对于特定基底的坐标的形式表示,以方便直观认知、计算处理。比如说,![]() 中相对于基底
中相对于基底![]() 的任意向量
的任意向量![]() 的坐标表示法(表示为列向量)如下所示:
的坐标表示法(表示为列向量)如下所示:
其中,![]() ,可以分别理解为向量
,可以分别理解为向量![]() 在两个基向量方向上的投影的代数长度。
在两个基向量方向上的投影的代数长度。
如果前后文不会出现混淆的话,坐标列向量右下角的关于基底的表示可以省略。
显而易见的是,向量本身是与基底无关的,而坐标则是与基底有关的。同一个向量 ![]() 在不同的基底下表示时所得到的坐标列向量是不同的。
在不同的基底下表示时所得到的坐标列向量是不同的。
顺便扯一句, 同一个向量 ![]() 在不同的基底下表示时所得到的坐标列向量可以相互转化,这个转化对应着线性映射,可以用矩阵来表示。
在不同的基底下表示时所得到的坐标列向量可以相互转化,这个转化对应着线性映射,可以用矩阵来表示。
2.8 计算基底 computational basis
虽然标准正交基相比任意的非标准正交基来说更容易处理,但是,也并非所有的标准正交基都同等地方便使用(人人生而平等,但是有些人比别人更平等一些^-^)。
在实际应用中,应该选择与实际情况最匹配最方便使用的标准正交基作为所有运算处理的基础,这个就称为计算基底。
比如说在量子力学中,电子的自旋有两个状态,一个是向上的自旋,一个是向下的自旋。它们可以用复希尔伯特空间![]() 中的一组基来表示这两个状态(也称为态矢量),它们构成了
中的一组基来表示这两个状态(也称为态矢量),它们构成了![]() 的一组标准正交基。由于电子经过观测后,必定会落到这两者之一,因此它们就是量子计算中最方便使用的标准正交基,可以作为计算基底使用。用下一节所介绍的狄拉克符号来表示的话记为
的一组标准正交基。由于电子经过观测后,必定会落到这两者之一,因此它们就是量子计算中最方便使用的标准正交基,可以作为计算基底使用。用下一节所介绍的狄拉克符号来表示的话记为![]() ,而在该计算基底下,
,而在该计算基底下,![]() 两者自身的坐标表示则显而易见的分别是:
两者自身的坐标表示则显而易见的分别是:
除了![]() ,量子计算中常见的标准正交基还有
,量子计算中常见的标准正交基还有![]() 、
、![]() ,后两组标准正交基就不如
,后两组标准正交基就不如![]() 那样适合用作计算基底。
那样适合用作计算基底。
计算基底的选择也只是一个约定俗成,并没有必然性,用![]() 或者
或者![]() 作为计算基底也未尝不可。但是有可能会让计算处理变得更麻烦一点!
作为计算基底也未尝不可。但是有可能会让计算处理变得更麻烦一点!
进一步,归根结底,这些都只是符号!是先选定了电子自旋的两个基态所对应的态矢量构成的计算基底,然后将它们命名为![]() ,而不是反过来! 数学工具使得物理的描述变得更方便(甚至是变得可能0,但是过于沉浸于数学的描述而忘记它们本来的物理含义则本末倒置了)
,而不是反过来! 数学工具使得物理的描述变得更方便(甚至是变得可能0,但是过于沉浸于数学的描述而忘记它们本来的物理含义则本末倒置了)
2.9 狄拉克符号
狄拉克符号是由狄拉克发明的用于量子力学中的向量表示方法,也称为bra-ket表示法(此bra非彼bra)。
给定一个向量![]() ,用
,用![]() 表示其对应的行向量表示,在量子力学语境中称为左矢,读作(bra-v);用
表示其对应的行向量表示,在量子力学语境中称为左矢,读作(bra-v);用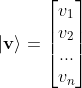 表示对应的列向量表示,称为右矢,读作(ket-v)。
表示对应的列向量表示,称为右矢,读作(ket-v)。
内积(点积,点乘)的表示:![]()
外积(外乘,叉乘)的表示:![]()
![]()
狄拉克符号表示好处在后面的讨论中将会逐渐显现出来。
相关博文:
量子笔记:酉矩阵(幺正矩阵)、量子门的可逆性
参考文献:
[1] 罗伯特.S.苏托尔 著,吴攀译:与量子比特共舞,人民邮电出版社
[2] 赵连阔,冯丽霞 编著:泛函分析初步教程,中国科学技术出版社
[3] 克里斯.伯恩哈特 著,邱道文 周旭 等译:人人可懂的量子计算