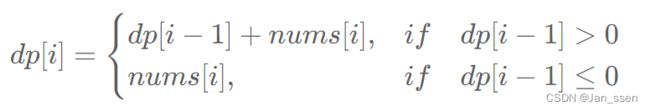简单的动态规划

首先，我们先来看一个最简单的动态规划问题——爬楼梯

题目：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

如果你是第一次看到这种问题，那么一脸懵是很正常的。我们不妨先进行列举：

• 如果是爬一层楼梯，只有一种方法
• 如果是爬两层楼梯，则可以一层一层爬，也可以一次爬两层，两种方法
• 如果是爬三层楼梯，则可以从一层直接爬两个台阶或者从二层爬一个台阶，共有1+2=3种方法
• 如果是爬四层楼梯，则可以从二层直接爬两个台阶或者从三层爬一个台阶，共有3+2=5种方法
• ……

大家有没有发现什么？如此推得，爬n层楼梯的方法数不就是爬n-1层楼梯的方法数+爬n-2层楼梯的方法数吗？

求得递推公式：f(n) = f(n-1)+f(n-2)

诶？！！！这不是斐波那契数列吗？最经典的递归算法，但是我们知道，递归的逐层嵌套是存在很大弊端的，我们能否对其进行一定的改进呢？接下来，就让我们有请今天的主人公——动态规划

---

既然每一层的方法都受前面层数的影响，那么我们不妨将每层所需的方法数存在一个数组里，这样以来要求哪一层就直接从数组里调就好了。

接下来，我们上代码：

    public int climbStairs(int n) {
        if (n <= 1)
            return 1;
        int[] dp = new int[n + 1];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];

分析一波复杂度——时间复杂度：O(n)，空间复杂度：O(n)。看到这个复杂度，仔细想想还有没有什么可优化的地方呢？？？

对！是空间！既然我们只需要第n层的方法，而求第n层只需要求前两层的方法，那我们把之前全部的方法数存起来干什么？直接创建两个变量每次存放前两层的方法数然后不断更新就好了呀！

优化后的代码：

    public int climbStairs(int n) {
        int q = 0;    //n-2层
        int p = 0;    //n-1层
        int r = 1;    //n层
        for(int i = 0;i < n;i++){
            q = p;
            p = r;
            r = p+q;
        }
        return r;
    }

直接空间复杂度降到常量级O(1)

这就是动态规划最基本的模型（可别小看了它，看起来容易，自己动手写起来可没那么简单hhh）

---

那么 （总结来啦！）我们在什么情况下应该使用动态规划呢？

摘自知乎——如果一个问题，可以把所有可能的答案穷举出来，并且穷举出来后，发现存在重叠子问题，就可以考虑使用动态规划。

动态规划的核心在于——(就本题举例）

• 拆分子问题：第n项可由n-1项和n-2项得出
• 记住过往：将每一层的方法数存起来
• 减少重复计算：如用递归，f(5) = f(4) + f(3)和 f(4) = f(3) + f(2)中f(3)的计算就重复了

动态规划的典型特征——（就本题举例）

• 边界：f(1)和f(2)是边界
• 状态转移方程：f(n) = f(n-1) + f(n-2)
• 最优子结构：由于f(n) = f(n-1) + f(n-2) ，则f(n-1)和f(n-2)就是f(n)的最优子结构
• 重叠子问题：同上的减少重复计算

动态规划的解题步骤：

1. 确定初始状态
2. 找到转移公式
3. 确定初始条件和边界条件
4. 计算结果

---

是不是有点意思啦！趁还热乎着，让我们再来道题试试手

题目：最大子序和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

 我们试着用动态规划来分析这道题：

第一步：确定初始状态

我们需要先建立连续子数组第n项的和与前一项的关系。(这一步很重要，只有找到dp[i]所代表的意义才能建立相应的转移公式）

假设dp[i]为以第i项结尾的连续子数组的最大和，

• 如果dp[i-1]大于0，证明以第i-1项结尾的连续子数组的最大和为正数，我们就能把第i项与之相连求最大和
• 如果dp[i-1]不大于0，证明把第i项与之相连只会让dp[i]变得更小，那么我们直接把nums[i]的值赋给dp[i]就好，即以以第i项结尾的连续子数组的最大和就是nums[i]自身

第二步：找到转移公式

由第一步的分析，我们可以求出dp[i]的公式为

 第三步：确定初始条件和边界条件

当i=0时，以第一项结尾的连续子数组的最大和就是它本身，所以dp[0] = nums[0]

好啦，既然我们的初始工作全部完毕，接下来就可以开始写代码了

public int maxSubArray(int[] num) {
    int length = num.length;
    int[] dp = new int[length];
    //边界条件
    dp[0] = num[0];
    int max = dp[0];
    for (int i = 1; i < length; i++) {
        //转移公式
        dp[i] = Math.max(dp[i - 1], 0) + num[i];
        //记录最大值
        max = Math.max(max, dp[i]);
    }
    return max;
}

同样，有没有什么地方可以简化呢？对，既然dp[i]只受dp[i-1]的影响，那岂不两个变量搞定？！！

优化后的代码：

    public int maxSubArray(int[] nums) {
        int dp1,dp2;
        dp1 = dp2 = nums[0];
        int max = nums[0];
        for(int i = 1;i < nums.length;i++){
            dp2 = dp1>0?dp1+nums[i]:nums[i];
            max = dp2>max?dp2:max;
            dp1 = dp2;
        }
        return max;
    }

以上是两道最为基础的动态规划问题，如果你已经学会了，那就快去找几道经典的动态规划问题去试试手吧！！！