OpenCV计算机视觉学习（4）——图像平滑处理（均值滤波，高斯滤波，中值滤波，双边滤波）

 

人工智能学习离不开实践的验证，推荐大家可以多在FlyAI-AI竞赛服务平台多参加训练和竞赛，以此来提升自己的能力。FlyAI是为AI开发者提供数据竞赛并支持GPU离线训练的一站式服务平台。每周免费提供项目开源算法样例，支持算法能力变现以及快速的迭代算法模型。

如果需要处理的原图及代码，请移步小编的GitHub地址

　　传送门：请点击我

　　如果点击有误：https://github.com/LeBron-Jian/ComputerVisionPractice

　　“平滑处理”（smoothing）也称“模糊处理”（bluring），是一项简单且使用频率很高的图像处理方法。平滑处理的用途有很多，最常见的是用来减少图像上的噪点或者失真。在涉及到降低图像分辨率时，平滑处理是非常好用的方法。

　　图像滤波，就是在尽量保留图像细节特征的条件下对目标图像的噪声进行抑制，是图像预处理中不可或缺的操作，其处理效果的好坏将直接影响到后续图像处理和分析的有效性和可靠性。

　　关于滤波，一种形象的比喻法是：我们可以把滤波器想象成一个包含加权系数的窗口，当使用这个滤波器平滑处理图像时，就把这个窗口放到图像之上，透过这个窗口来看我们得到的图像。而对滤波处理的要求有两个，一是不能损坏图像的轮廓及边缘等重要信息；二是使图像清晰视觉效果好。

　　在学习这几种滤波之前，我们首先记住两句话：

• 1，滤波是掩膜（mask）和图像的卷积。
• 2，滤波过程分为：（1）计算掩膜   （2）卷积  ——掩膜上每一个位置的值和图像上对应位置的像素值的乘加运算。

 　　这里对几个滤波函数做一下笔记，下面这两个图呢，是盗的，主要是人家写的好。哈哈哈哈，侵删啊！

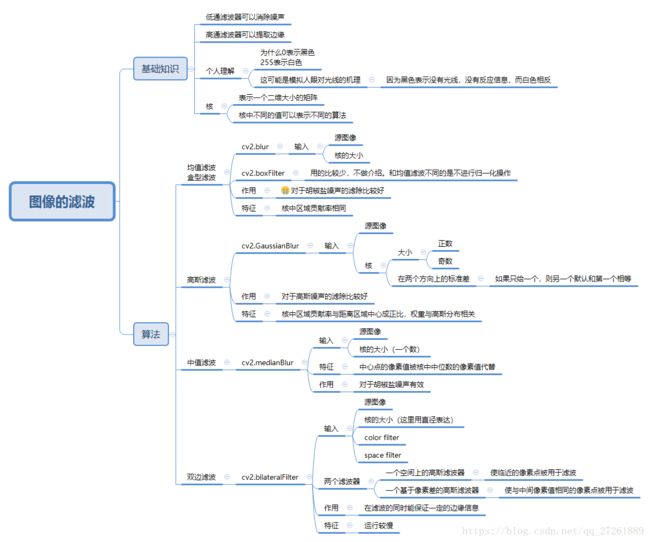
　　具体模糊和滤波的关系如下图（https://www.zhihu.com/question/54918332/answer/142137732）：

1，均值滤波（Mean Filtering）

　　均值滤波（低通滤波）是典型的线性滤波算法，它是指在图像上对目标像素给一个模板，该模板包括了其周围的临近像素（以目标像素为中序的周围八个像素，构成一个滤波模板，即去掉目标像素本身），再用模板中的全体像素的平均值来代替原来像素值。

　　简单来说，图片中一个方块区域 N*M 内，中心点的像素为全部点像素值的平均值。均值滤波就是对整张图片进行以上操作。

　　我们可以看下图的矩阵进行理解：

 　　进而我们可以看下图（盗图，侵删https://blog.csdn.net/Eastmount/article/details/82216380），红色点的像素值为蓝色背景区域像素值之和除25。

 　　其中红色区域的像素值均值滤波处理过程为： ((197+25+106+156+159)+ (149+40+107+5+71)+ (163+198+226+223+156)+ (222+37+68+193+157)+ (42+72+250+41+75)) / 25 = 125.52

　　其中5*5的矩阵称为核，针对原始图像内的像素点，采用核进行处理，得到结果图像。

 　　提取1/25 可以将核转换为如下形式：

 　　就是我们上面的公式。

1.1，均值滤波函数Blur

　　Python调用OpenCV实现均值滤波的核心函数如下：

1	blur(src, ksize, dst=None, anchor=None, borderType=None)

　　参数详情：

• src参数表示待处理的输入图像。
• ksize参数表示模糊内核大小。比如(1,15)表示生成的模糊内核是一个1*15的矩阵。
• dst参数表示输出与src相同大小和类型的图像。
• anchor参数、borderType参数可忽略

 　　其中，核大小是以（宽度，高度）表示的元组形式。常见的形式包括：和大小（3， 3）和（5， 5）：

　　均值滤波实现代码如下：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

#_*_coding:utf-8_*_ import cv2 import matplotlib.pyplot as plt     def blur_filter_func(filename):     img = cv2.imread(filename)     rgbimg = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)       # 均值滤波: 简单的平均卷积操作     result = cv2.blur(img, (5, 5))     # 显示图像     titles = ['origin image', 'blur image']     images = [rgbimg, result]     for i in range(2):         plt.subplot(1, 2, i+1), plt.imshow(images[i])         plt.title(titles[i])         plt.xticks([]), plt.yticks([])     plt.show()   if __name__ == '__main__':     filename = 'lenaNoise.png'     blur_filter_func(filename)

 

　　效果如下：

1.2，均值滤波优缺点

优点：

　　效率高，思路简单

缺点：

　　均值滤波本身存在着固有的缺陷，即它不能很好地保护图像细节，在图像去噪的同时也破坏了图像的细节，从而使图像变得模糊，不能很好地去除噪声点，特别是椒盐噪声。

　　这就要开始提到我们的高斯滤波了。

　　高斯滤波器是一种现性滤波器，能够有效地抑制噪声，平滑图像。其作用原理和均值滤波器类似，都是取滤波器窗口内像素的均值作为输出。其窗口模板的稀疏和均值滤波器不同，均值滤波器的模板稀疏都是相同的为1；而高斯滤波器的模板稀疏，则随着距离模板中心的增大而系数减少。所以，高斯滤波器相比于均值滤波器对图像的模型程度较小。

1.3 方框滤波（盒子滤波）

　　方框滤波比均值滤波多一个参数。此参数为normalize，当 normalize=True时，与均值滤波结果相同，normalize=False，表示对加和后的结果不进行平均操作，大于255的使用255表示。

　　方框滤波BoxFilter()的实现代码：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

def BoxFilter(Imge,dim,dim2,flag):       #Image为待处理图像，dim为滤波器的大小dim*dim2     im=array(Imge)     #序列化     sigema=0     #滤波求和        for i in range(int(dim/2), im.shape[0] - int(dim/2)):         for j in range(int(dim2/2), im.shape[1] - int(dim2/2)):             for a in range(-int(dim/2), -int(dim/2)+dim):                 for b in range(-int(dim2/2), -int(dim2/2)+dim2):                     sigema = sigema + img[i + a, j + b]                     #对于滤波范围内求和，从左到右，从上到下扫                if(flag):                 im[i, j] = sigema / (dim*dim2)                else:                 im[i,j]=min(sigema,255)             #归一化则与均值滤波一致，不归一化的话超过255用255表示             sigema = 0             #滤波移动     return im     原文链接：https://blog.csdn.net/zjyang12345/java/article/details/103358260

 

　　用途：非归一化（normalized = False）的方框滤波用于计算每个像素领域内的积分特性，比如密集光流算法（dense optical flow algorithms）中用到的图像倒数的协方差矩阵（convariance matrices of image derivatives）。

　　选择归一化后，方框滤波与均值滤波结果相同，不选择容易越界，越界的话，超过255则用255表示。

　　下面使用OpenCV代码实现：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

#_*_coding:utf-8_*_ import cv2 import matplotlib.pyplot as plt     def box_blur_filter_func(filename):     img = cv2.imread(filename)     rgbimg = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)       blur = cv2.blur(img, (3, 3))     # 方框滤波: 基本和均值滤波一样，可以选择归一化，如果选择归一化，则和均值滤波一样     # 如果不选择归一化，则方框滤波容易越界，越界的话，超过255则用255表示     result_normal = cv2.boxFilter(img, -1, (3, 3), normalize=True)     result_nonormal = cv2.boxFilter(img, -1, (3, 3), normalize=False)     # 显示图像     titles = ['origin image', 'boxFilter image no normalize', 'boxFilter image normalize', 'blut filter image']     images = [rgbimg, result_nonormal, result_normal, blur]     for i in range(4):         plt.subplot(2, 2, i+1), plt.imshow(images[i])         plt.title(titles[i])         plt.xticks([]), plt.yticks([])     plt.show()   if __name__ == '__main__':     filename = 'lenaNoise.png'     box_blur_filter_func(filename)

 　　效果图如下：

2，高斯滤波（高斯模糊）（Gaussian Filtering）

　　通常，图像处理软件会提供“模糊”（blur）滤镜，使图片产生模糊的效果。“模糊”的算法有很多种，这里我们首先学习“高斯模糊”（Gaussian Blur）。它将正态分布（“高斯分布”）用于图像处理中。本质上，高斯滤波是一种数据平滑的技术（data smoothing），适用于多个场景，图像处理恰好提供了一个直观的应用实例。

2.1，高斯滤波的原理

　　（PS：其实高斯滤波和高斯模糊是一个意思，为什么叫高斯模糊呢，就是这个滤波的效果看起来像是把图像给弄模糊了，所以又有了“高斯模糊”的叫法，而后面为了统一，这里我都叫高斯滤波）

　　既然认真学习原理了，这里我们首先对高斯函数做一个认真的学习。

　　高斯分布其实学名叫正态分布（Normal distribution），正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。

　　高斯分布公式如下：

 　　其中，μ是x的均值，σ是x的方差。因为计算平均值的时候，中心点就是原点，所以μ等于0。 

 　　根据一维高斯函数，可以推导出二维高斯函数：

 　　形状如下：

 　　上图为一维高斯分布示意图， μ 觉得了分布对称中心， σ  决定了分布的形状， σ 越小形状越瘦小， σ  越大越矮胖。所以就是越接近中心，取值越大，越远离中心，取值越小。计算平均值的时候，我们只需要将“中心点”作为原点，其他店按照其在正态曲线上的位置，分配权重，就可以得到一个加权平均值。

　　那高斯分布公式的作用到底是什么呢？——计算高斯滤波用的掩膜（mask）。

　　掩膜是什么呢？下面我们首先来一个3*3的均值滤波的掩膜：

 　　可以看到，均值掩膜内所有稀疏均相等，为1/9，且他们的和为1，同理可得5*5均值滤波的掩膜。在“中间点” 取“周围点” 的平均值，就变为周围的平均值了，在数值上，这是一种“平滑化”，在图形上，就相当于产生“模糊”效果，“中间点” 失去细节。显然，计算平均值时，取值范围越大，“模糊效果”越强烈。

　　这里我们分析了均值滤波，后面学到均值滤波的时候就略过了。

　　下面计算权重矩阵。

 　　对于图像中任意一点（x,  y），它周围的坐标为：（这里直接盗图，方便）

 　　例如：要产生一个高斯滤波模板，以模板的中心位置为坐标原点进行取样。模板在各个位置的坐标，如下图所示（x轴水平向右，y轴竖直向下），我们用数值代替上面（x,  y），假定中心点的坐标为（0,  0），那么距离它周围的八个点的坐标如下：

 　　更远的点，依次类推，为了计算权重矩阵，需要设定 σ 的值，假定  σ = 1.5 ，则模糊半径为1的权重矩阵如下：

 　　这九个点的权重综合等于 0.4787147，如果只计算这 9 个点的加权平均，还必须让他们的权重之和等于1，因此上面的九个值还要分别除以  0.4787147，得到最终的权重矩阵：

 　　有了权重矩阵，就可以计算高斯模糊的值了。假设现有九个像素点，灰度值（0-255）如下：

 　　每个点乘以自己的权重值：

 　　得到：

 　　将这九个值加起来，就是中心点的高斯模糊的值，对所有的点重复这个过程，就得到了高斯模糊后的图像。如果原图是彩色的图像，可以对RBG三个通道分别做高斯模糊。

　　（PS：非常感谢https://blog.csdn.net/jiandanjinxin/article/details/51281828这篇博客做的图）

 　　最后再在网上盗个图，展示下利用高斯掩膜和图像进行卷积求解高斯模糊：

　　　　　　　　　　                        117 = 102 * 0.075 + 108 * 0.124 + 110 * 0.075 +119 * 0.124 + 120 * 0.204 + 110 * 0.124+129 * 0.075 + 130 * 0.124 + 132 * 0.075

　　130 = 172 * 0.075 + 175 * 0.124 + 172 * 0.075 +112 * 0.124 + 123 * 0.204 + 88 * 0.124 +98* 0.075 + 115 * 0.124 + 128 * 0.075

 　　所有像素都用图上的那一套模板进行卷积运算，最终得到滤波的结果。这样就可以让一个完整的高斯滤波的原理展示出来，我也理解了，谢谢各位网友。

 

这样计算出来的模板有两种形式：小数和整数

1，小数形式的模板，就是直接计算得到的值，没有经过任何的处理

2，整数形式的模板，则需要进行归一化，将模板左上角的值归一化为1

 

2.2，高斯滤波函数GaussianBlur

　　函数原型：

1	GaussianBlur(src, ksize, sigmaX, dst=None, sigmaY=None, borderType=None)

　　变量的含义：

• src参数表示待处理的输入图像。
• ksize参数表示高斯滤波器模板大小。 ksize.width和ksize.height可以不同，但它们都必须是正数和奇数。或者，它们可以是零，即（0, 0），然后从σ计算出来。
• sigmaX参数表示 X方向上的高斯内核标准差。
• sigmaY参数表示 Y方向上的高斯内核标准差。 如果sigmaY为零，则设置为等于sigmaX，如果两个sigma均为零，则分别从ksize.width和ksize.height计算得到。

　　补：若ksize不为(0, 0)，则按照ksize计算，后面的sigmaX没有意义。若ksize为(0, 0)，则根据后面的sigmaX计算ksize。

　　比如常用的如下：

1	blurred = cv2.GaussianBlur(gray, (9, 9),0)

　　高斯模糊本质上是低通滤波器，输出图像的每个像素点是原图像上对应像素点与周围像素点的加权和。

　　高斯矩阵的尺寸和标准差：（9， 9）表示高斯矩阵的长和宽，标准差取0时，OpenCV会根据高斯矩阵的尺寸自己计算，高斯矩阵的尺寸越大，标准差越大，处理过的图像模糊程度越大。

　　高斯平滑与简单平滑不同，它在对领域内像素进行平均时，给与不同位置的像素不同的权值，下面所示的是 3*3 和 5*5 领域的高斯模板。

 　　代码如下：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

#_*_coding:utf-8_*_ import cv2 import matplotlib.pyplot as plt     def gaussian_blur_func(filename):     img = cv2.imread(filename)     rgbimg = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)       # 高斯滤波：高斯模糊的卷积核的数值是满足高斯分布的，相当于更重视中间的     # 标准差取0时，OpenCV会根据高斯矩阵的尺度自己计算     result1 = cv2.GaussianBlur(img, (5, 5), 0)     result2 = cv2.GaussianBlur(img, (5, 5), 1)     # 显示图像     titles = ['origin image', 'gaussian blur image stu 0', 'gaussian blur image stu 1']     images = [rgbimg, result1, result2]     for i in range(3):         plt.subplot(1, 3, i+1), plt.imshow(images[i])         plt.title(titles[i])         plt.xticks([]), plt.yticks([])     plt.show()   if __name__ == '__main__':     filename = 'lenaNoise.png'     gaussian_blur_func(filename)

 　　效果图如下：

 　　其实理解了过程，我们也可以自己写出高斯滤波的源码，简单来说就是归一化，灰度化，然后遍历灰度图像素点，对响度点领域进行高斯滤波，这里就不写了，直接展示代码。

　　代码如下：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49

import cv2 as cv import math import numpy as np   # 灰度化处理 def rgb2gray(img):     h=img.shape[0]     w=img.shape[1]     img1=np.zeros((h,w),np.uint8)     for i in range(h):         for j in range(w):             img1[i,j]=0.144*img[i,j,0]+0.587*img[i,j,1]+0.299*img[i,j,1]     return img1   # 计算高斯卷积核 def gausskernel(size):     sigma=1.0     gausskernel=np.zeros((size,size),np.float32)     for i in range (size):         for j in range (size):             norm=math.pow(i-1,2)+pow(j-1,2)             gausskernel[i,j]=math.exp(-norm/(2*math.pow(sigma,2)))   # 求高斯卷积     sum=np.sum(gausskernel)   # 求和     kernel=gausskernel/sum   # 归一化     return kernel   # 高斯滤波 def gauss(img):     h=img.shape[0]     w=img.shape[1]     img1=np.zeros((h,w),np.uint8)     kernel=gausskernel(3)   # 计算高斯卷积核     for i in range (1,h-1):         for j in range (1,w-1):             sum=0             for k in range(-1,2):                 for l in range(-1,2):                     sum+=img[i+k,j+l]*kernel[k+1,l+1]   # 高斯滤波             img1[i,j]=sum     return img1   image = cv.imread("lenaNoise.png") grayimage=rgb2gray(image) gaussimage = gauss(grayimage) cv.imshow("image",image) cv.imshow("grayimage",grayimage) cv.imshow("gaussimage",gaussimage) cv.waitKey(0) cv.destroyAllWindows()

　　效果图如下：

 

3，双边滤波

　　双边滤波其实很简单，它只是比高斯滤波多了一种掩膜而已。两种掩膜都是套用高斯分布公式得到的。双边滤波不光考虑了像素在空间中位置远近程度的影响，还考虑了像素亮度相近程度的影响。

　　双边滤波（Bilateral filter）是一种非线性的滤波方法，是结合图像的空间邻近度和像素值相似度的一种折中处理，同时考虑空域信息和灰度相似性，达到保边去噪的目的。双边滤波器顾名思义比高斯滤波多了一个高斯方差sigma－d，它是基于空间分布的高斯滤波函数，所以在边缘附近，离的较远的像素不会太多影响到边缘上的像素值，这样就保证了边缘附近像素值的保存。但是由于保存了过多的高频信息，对于彩色图像里的高频噪声，双边滤波器不能够干净的滤掉，只能够对于低频信息进行较好的滤波。

　　双边滤波在滤波的同时能保证一定的边缘信息，但是运行较慢。

3.1双边滤波函数（BilateralFilter ）

　　函数如下：

1	bilateralFilter(src, d, sigmaColor, sigmaSpace, dst=None, borderType=None)

　　参数如下：

• src参数表示待处理的输入图像。
• d参数表示在过滤期间使用的每个像素邻域的直径。如果输入d非0，则sigmaSpace由d计算得出，如果sigmaColor没输入，则sigmaColor由sigmaSpace计算得出。
• sigmaColor参数表示色彩空间的标准方差，一般尽可能大。较大的参数值意味着像素邻域内较远的颜色会混合在一起，从而产生更大面积的半相等颜色。
• sigmaSpace参数表示坐标空间的标准方差(像素单位)，一般尽可能小。参数值越大意味着只要它们的颜色足够接近，越远的像素都会相互影响。当d > 0时，它指定邻域大小而不考虑sigmaSpace。 否则，d与sigmaSpace成正比。

 　　实现代码如下：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

#_*_coding:utf-8_*_ import cv2 import matplotlib.pyplot as plt     def bilateral_filter_func(filename):     img = cv2.imread(filename)     rgbimg = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)       # 双边滤波：它能保持边界清晰的情况下有效的去除噪声，但是这种操作比较慢     # 双边滤波拥有美颜的效果     bilateral_filter = cv2.bilateralFilter(img, d=0, sigmaColor=100, sigmaSpace=15)     # 显示图像     titles = ['origin image', 'bilteral filter image']     images = [rgbimg, bilateral_filter]     for i in range(2):         plt.subplot(1, 2, i+1), plt.imshow(images[i])         plt.title(titles[i])         plt.xticks([]), plt.yticks([])     plt.show()   if __name__ == '__main__':     filename = 'lenaNoise.png'     bilateral_filter_func(filename)

 　　效果如下：

4，中值滤波（Median Filtering）

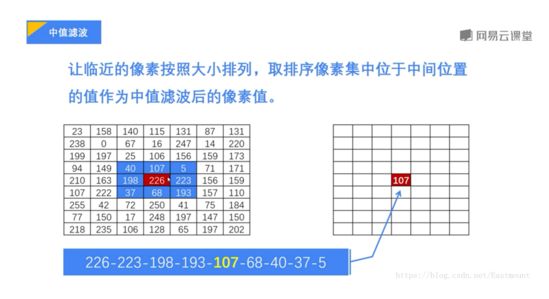
　　中值滤波是一种非线性数字滤波器技术，经常用于去除图像或者其他信号中的噪声，是处理椒盐噪声的常用降噪算法。中值滤波将每一像素点的灰度值设置为该点某领域窗口内的所有像素点灰度值的中值。

 　　在使用邻域平均法去噪的同时也使得边界变得模糊。而中值滤波是非线性的图像处理方法，在去噪的同时可以兼顾到边界信息的保留。选一个含有奇数点的窗口W，将这个窗口在图像上扫描，把窗口中所含的像素点按灰度级的升或降序排列，取位于中间的灰度值来代替该点的灰度值。 例如选择滤波的窗口如下图，是一个一维的窗口，待处理像素的灰度取这个模板中灰度的中值，滤波过程如下：

 　　图像平滑里中值滤波的效果最好。

4.1，中值滤波函数（MedianBlur ）

　　OpenCV主要调用函数如下：

1	medianBlur(src, ksize, dst=None)

　　参数意义：

• src参数表示待处理的输入图像。
• ksize参数表示滤波窗口尺寸，必须是奇数并且大于1。比如这里是5，中值滤波器就会使用5×5的范围来计算，即对像素的中心值及其5×5邻域组成了一个数值集，对其进行处理计算，当前像素被其中值替换掉。
• dst参数表示输出与src相同大小和类型的图像。

　　代码如下：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

#_*_coding:utf-8_*_ import cv2 import matplotlib.pyplot as plt     def median_blur_filter_func(filename):     img = cv2.imread(filename)     rgbimg = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)       # 中值滤波: 相当于用中值代替     median = cv2.medianBlur(img, 5)     # 显示图像     titles = ['origin image', 'blut filter image']     images = [rgbimg, median]     for i in range(2):         plt.subplot(1, 2, i+1), plt.imshow(images[i])         plt.title(titles[i])         plt.xticks([]), plt.yticks([])     plt.show()   if __name__ == '__main__':     filename = 'lenaNoise.png'     median_blur_filter_func(filename)

　　效果如下：

4.2，窗口问题

　　中值滤波降噪的原理为使用噪点的某一个邻域内的中值代替该噪点，邻域范围越大则边缘保留效果越差，从视觉上来看，即更加模糊，但降噪效果明显。此外，邻域亦即窗口的形状也会影响降噪的效果。通常有3*3  5*5 ，十字形，圆形等。这里此文采用十字形

　　常用的窗口还有方形、十字形、圆形和环形。不同形状的窗口产生不同的滤波效果，方形和圆形窗口适合外轮廓线较长的物体图像，而十字形窗口对有尖顶角状的图像效果好。中值滤波对于消除孤立点和线段的干扰十分有用，尤其是对于二进噪声，但对消除高斯噪声的影响效果不佳。对于一些细节较多的复杂图像，可以多次使用不同的中值滤波。

 　　代码如下：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52

import numpy as np import random   def median_filtering(input_signal):     '''     中值滤波（适用于灰度图）     如：             - + -             + * +             - + -     * 为噪点，滤波方法为：取4个+的中位数（若某+不在输入信号范围内，则随机添加0或255）     :param input_signal: 输入信号矩阵（2D）     :return: 滤波后的信号     '''     salt_pepper = [0, 255]       m, n = input_signal.shape  # 获取输入图片的尺寸（行和列）       input_signal_cp = input_signal.copy()   # 输入信号的副本       nosiy_data_around = []  # 存放噪点上下左右的数据点     # 遍历滤波     for i in range(m):         for j in range(n):             # 当灰度值为0或255时，则认为该数据点为椒盐噪点             if input_signal_cp[i, j] == 255 or input_signal_cp[i, j] == 0:                 # 每次无效数据点（即不再范围内）为4，每有一个在范围内，即-1                 invalid_data_per = 4                 if i + 1 < n:                     nosiy_data_around.append(input_signal_cp[i + 1, j])                     invalid_data_per = invalid_data_per - 1                 if i - 1 >= 0:                     nosiy_data_around.append(input_signal_cp[i - 1, j])                     invalid_data_per = invalid_data_per - 1                 if j + 1 < m:                     nosiy_data_around.append(input_signal_cp[i, j + 1])                     invalid_data_per = invalid_data_per - 1                 if j - 1 >= 0:                     nosiy_data_around.append(input_signal_cp[i, j - 1])                     invalid_data_per = invalid_data_per - 1                 else:                     if invalid_data_per > 0:                         # 根据无效数据点的个数，随机添加0或255                         for k in range(invalid_data_per):                             nosiy_data_around.append(salt_pepper[random.randint(0, 1)])                 # 取中位数                 input_signal_cp[i, j] = np.median(nosiy_data_around)                   # 该噪点的周围数据数组清空，为下一个噪点周围数据存在做准备                 nosiy_data_around = []       return input_signal_cp

　　

5，几种滤波的代码实现

 　　代码如下：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

import numpy as np import cv2 import matplotlib.pyplot as plt ########     四个不同的滤波器    ######### img = cv2.imread('cat.jpg')   # 均值滤波 img_mean = cv2.blur(img, (5,5))   # 高斯滤波 img_Guassian = cv2.GaussianBlur(img,(5,5),0)   # 中值滤波 img_median = cv2.medianBlur(img, 5)   # 双边滤波 img_bilater = cv2.bilateralFilter(img,9,75,75)   # 展示不同的图片 titles = ['srcImg','mean', 'Gaussian', 'median', 'bilateral'] imgs = [img, img_mean, img_Guassian, img_median, img_bilater]   for i in range(5):     plt.subplot(2,3,i+1)#注意，这和matlab中类似，没有0，数组下标从1开始     plt.imshow(imgs[i])     plt.title(titles[i]) plt.show()

　　效果图如下：

 

6，椒盐噪声与中值滤波的Python实现与检验

6.1  椒盐噪声（Salt Pepper Noise）

　　椒盐噪声也称为脉冲杂讯，是图像中经常见到的一种杂讯，它是一种随机出现的白电或者黑点，可能是亮的区域有黑色像素或是在暗的区域有白色像素（或者两者皆有）——维基百科

关于椒盐噪声的几点注意

• 噪声类型随机，即亮斑或暗斑（对应灰度图0,255）
• 噪声概率为先验概率（如噪声概率为0.1，数据点总数为1000），而实际的噪声点并不一定为10,

6.2  椒盐噪声实现算法思路

• 1，新建一个与输入图像等长的数组
• 2，数组中存放（1,100/（100*noisy probability））的随机整数
• 3，当上述数组中出现的值为1时，则认为对应的数据点为噪点
• 4，该噪点等概率的取亮斑或暗斑（0， 255）

　　代码如下：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

import numpy as np import random   def salt_pepper(intput_signal, probability):     '''     椒盐噪声算法（适用于灰度图）     :param intput_signal: 输入信号矩阵（2D）     :param probability: 噪声概率（如：0.1为10%）     :return: 加噪后的图像、实际噪点数、理论噪点数     '''     nisy = [0, 255] # 噪声（salt， papper）       m, n= intput_signal.shape  # 获取输入图片尺寸(行和列)       intput_signal_cp = intput_signal.copy() # 输入信号的副本     intput_signal_cp = intput_signal_cp.reshape(-1) # reshape为一个行向量       # 该噪声概率下，理论上noisy_data_probability_num个数据点中1一个噪点     noisy_data_probability_num = int(100 / (probability * 100))       # 噪点数组，当数组中的值为1时，则认为对应的数据点为噪点     noisy_data = []     for i in range(m*n):         noisy_data.append(random.randint(1, noisy_data_probability_num))       # 实际噪点数与理论噪点数     actual_noisy_data_num = 0     theory_noisy_data_num = int(m * n * probability)       # 添加噪点     for i in range(m*n):         if noisy_data[i] == 1:             actual_noisy_data_num = actual_noisy_data_num + 1             intput_signal_cp[i] = nisy[random.randint(0, 1)]       # 重塑至m*n的矩阵     intput_signal_cp = intput_signal_cp.reshape(m, n)       return  intput_signal_cp, actual_noisy_data_num, theory_noisy_data_num

 

6.3  中值滤波抑制噪声

　　受光照、气候、成像设备等因素的影响，灰度化后的图像存在噪声和模糊干扰，直接影响到下一步的文字识别，因此，需要对图像进行增强处理。图片预处理中重要一环就是椒盐去澡，通常用到中值滤波器进行处理，效果很好。中值滤波器是一种非线性滤波器，其基本原理是把数字图像中某点的值用其领域各点值的中值代替。如求点[i,j]的灰度值计算方法为：（1）按灰度值顺序排列[i,j]领域中的像素点；（2）取排序像素集的中间值作为[i,j]的灰度值。中值滤波技术能有效抑制噪声。

　　直接上代码，希望给大家有帮助：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

import numpy as np import cv2 import tensorflow as tf from PIL import Image import os import scipy.signal as signal   input_images = np.zeros((300, 300)) filename = "D:\字母图库\F\P80627-112853.jpg" print(filename) img = Image.open(filename).resize((300, 300)).convert('L') width = img.size[0] height = img.size[1]   for h in range(0, height):     for w in range(0, width):         if img.getpixel((h, w)) < 128:             input_images[w, h] = 0         else:             input_images[w, h] = 1 cv2.imshow("test1111", input_images)   data = signal.medfilt2d(np.array(img), kernel_size=3)  # 二维中值滤波 for h in range(0, height):     for w in range(0, width):         if data[h][w] < 128:             input_images[w, h] = 0         else:             input_images[w, h] = 1 cv2.imshow("test2222", input_images)   data = signal.medfilt2d(np.array(img), kernel_size=5)  # 二维中值滤波 for h in range(0, height):     for w in range(0, width):         if data[h][w] < 128:             input_images[w, h] = 0         else:             input_images[w, h] = 1 cv2.imshow("test3333", input_images) cv2.waitKey(0)

　　

 

6.4  高斯噪声的Python实现

　　在处理图像的时候，有时候可能我们需要给图像添加高斯噪声或者椒盐噪声，下面学习一下如何添加高斯噪声和椒盐噪声的代码。

　　首先，我们先定义高斯噪声函数 GaussianNoise(src,  means, sigma)，通过次函数生成均值为 means，标准差为 sigma的高斯白噪声。

　　椒盐噪声又称脉冲噪声，它是一种随机出现的白点或者黑点。椒盐噪声=椒噪声+盐噪声，椒盐噪声的值为0（黑色）或者255（白色），这里假设为等概率的出现0或者255。

　　下面直接上代码：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66

import random import cv2 from numpy import random     def GaussianNoise(src, means, sigma, percetage):     NoiseImg = src     NoiseNum = int(percetage * src.shape[0] * src.shape[1])     for i in range(NoiseNum):         randX = random.randint(0, src.shape[0] - 1)         randY = random.randint(0, src.shape[1] - 1)         # NoiseImg[randX, randY] = NoiseImg[randX, randY] + random.gauss(means, sigma)         NoiseImg[randX, randY] = NoiseImg[randX, randY] + random.normal(means, sigma)         if NoiseImg[randX, randY] < 0:             NoiseImg[randX, randY] = 0         elif NoiseImg[randX, randY] > 255:             NoiseImg[randX, randY] = 255     return NoiseImg     def PepperandSalt(src, percetage):     NoiseImg = src     NoiseNum = int(percetage * src.shape[0] * src.shape[1])     for i in range(NoiseNum):         #椒盐噪声图片边缘不处理，故-1         randX = random.random_integers(0, src.shape[0] - 1)         randY = random.random_integers(0, src.shape[1] - 1)         if random.random_integers(0, 1) <= 0.5:             NoiseImg[randX, randY] = 0         else:             NoiseImg[randX, randY] = 255     return NoiseImg     def imageSumPepperandSalt(origin_path, save_path):     img = cv2.imread(origin_path, 0)     img1 = PepperandSalt(img, 0.2)     cv2.imwrite(save_path, img1)     cv2.imshow('PepperandSalt', img1)     cv2.waitKey(0)     cv2.destroyAllWindows()     def imageSumGaussianNoise(origin_path, save_path):     img = cv2.imread(origin_path, 0)     img1 = GaussianNoise(img, 2, 4, 0.8)     cv2.imwrite(save_path, img1)     cv2.imshow('GaussianNoise', img1)     cv2.waitKey(0)     cv2.destroyAllWindows()   def origin_show(origin_path):     img = cv2.imread(origin_path, )     # 灰度化     # img = cv2.imread(origin_path, 0)     cv2.imshow('origin', img)     cv2.waitKey(0)     cv2.destroyAllWindows()   if __name__ == '__main__':     origin_path = 'butterfly.jpg'     save_path1 = 'butterfly_Gaussian.jpg'     save_path2 = 'butterfly_Salt.jpg'     origin_show(origin_path)     imageSumGaussianNoise(origin_path, save_path1)     imageSumPepperandSalt(origin_path, save_path2)

　　查看效果：

　　从左到右依次是 原图，灰度化图片，椒盐噪声图片，高斯噪声图片

 

参考文献：

那张总结图的来源：https://blog.csdn.net/xv1356027897/article/details/80099027

https://blog.csdn.net/nima1994/article/details/79776802

中值均值：https://blog.csdn.net/qinghuaci666/article/details/81737624

高斯滤波源码实现：https://blog.csdn.net/Skymelu/article/details/89086888

均值漂移原理：

https://blog.csdn.net/dcrmg/article/details/52705087 

https://blog.csdn.net/qq_23968185/article/details/51804574

https://blog.csdn.net/jinshengtao/article/details/30258833

用户自定义模糊，均值模糊，中值模糊：https://www.cnblogs.com/FHC1994/p/9097231.html

 方框滤波：https://blog.csdn.net/Eastmount/article/details/82216380

https://blog.csdn.net/kaikai______/article/details/53535909

更多精彩内容请访问FlyAI-AI竞赛服务平台；为AI开发者提供数据竞赛并支持GPU离线训练的一站式服务平台；每周免费提供项目开源算法样例，支持算法能力变现以及快速的迭代算法模型。

挑战者，都在FlyAI！！！