蓝桥杯2022年（本科c++b组）

目录

一：刷题统计

二：修剪灌木

三：X进制减法

四：统计子矩阵

五：积木画

六：扫雷

七：李白打酒加强版

八：砍竹子

---

一：刷题统计

 题目链接：4402. 刷题统计 - AcWing题库

因为本人补题都是在acwing上面，所以所有题目链接都会是acwing，大家也可以在c语言网上提交，题目数据都是相同的，都可以提交，额，y总有道题目修改了时间，延长了，大家可以自行寻找；

第一道题目很简单，就是计算时间的，但是这道题目通过率很低，第一次做的时候我也是出了麻烦，反正就是过不去，参考了各路大神的答案之后做了出来，这道题目并不困难。

#include

using namespace std;

typedef long long LL;

int main()
{
	LL a,b,n;
	cin>>a>>b>>n;
	LL k=a*5+b*2;//思想就是把七天除完，余下不足七天在计算
	LL t=n/k*7;
	n%=k;
	
	for(int i=0;i<5&&n>0;i++) t++,n-=a;
	for(int i=0;i<2&&n>0;i++) t++,n-=b;
	
	cout<

二：修剪灌木

题目链接：4403. 修剪灌木 - AcWing题库

实际观察后发现，非常简单的一道题目，某个点草长到最大高度等于他最长边的二倍；如果有五个灌木，第一个灌木被修剪过后，第二次修剪前，他的右边灌木都被修剪了两次，所以它的长度为8，第二个灌木被修剪前，要么是左边总共修剪两次，要么是右边被修剪两次，取最长，答案是6；

这样递推即可算出答案，代码非常简单；

#include

using namespace std;


int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
		cout<<2*max(i-1,n-i)<

三：X进制减法

题目链接：4404. X 进制减法 - AcWing题库

这道题目的难度实际上是小于大家想象的，好多同学看了一遍题目发现和进制有关，还好麻烦，就不想写，实际上这道题目并没有那么难啊（虽然我也是马后炮..）

我们再次仔细阅读题目，实际就是给你两个数，这两个数前后每一位进制都不相同，但是他们的对应位进制相同，比如a的十位和个位进制不同，但是a的十位和b的十位进制相同，我么你这里要求让a严格大于b，求出当所有位进制不确定，a-b的最小值可能是多少？

我们发现，这里我们a和b的每一位进制都是相同的，也就是二者用的同一进制规则，如果要让a-b最小，我们得保证每一位ai-bi之后最小，这样所有位化为十进制才最小。

这里有一个限制是我们不能超过最大位数，但是题目也不可能给你大于等于最大位数的数，最大也就是n，而且每一位的进制是自己判断的，所以基本可以知道n没啥用；

我们如何让每一位最小呢？答案是，取ai与bi两个数最大数加一为这位的进制，为什么呢？

比如3与5，我们让进制为6，这样abs（3-5）就达到了最小；

于是依据这个思想，我们就可以求解了；

那么如何求解a和b在进制下的结果呢？依然是最经典的海伦-秦九韶算法，这里不会的同学可以自行去学习一下这个方法；

代码如下：

#include
#include
#include
using namespace std;

typedef long long LL;

LL mod=1000000007;
int n,a,b;
int an[100010],bn[100010];

int main()
{
	cin>>n;
	cin>>a;
	for(int i=a;i>=1;i--) cin>>an[i];//这里我们需要的是低位对齐进行减法，高位不用管 
	cin>>b;
	for(int i=b;i>=1;i--) cin>>bn[i];//依然是从低位在0处 
	
	LL ans=0;
	for(int i=a;i>=1;i--)//这里不需要取a与b的最高位啊，因为a是严格大于b的，如果位数a

四：统计子矩阵

题目链接：4405. 统计子矩阵 - AcWing题库

这道题目非常麻烦啊，我发现蓝桥杯的题目就是，题面看着巨简单，但是你得思考，而且用的算法或者是方法如果你没见过或者学过，那估计你得寄；

这道题目就属于极简的题面，但是却不好做；

首先我们需要计算出二维前缀和，这里的方法就是简单的二维前缀和，算出来前缀和，我们就需要统计子矩阵里有多少个矩阵的大小小于等于K，这里的统计如果大家不会优化的话，就只能暴力循环，枚举子矩阵四个点进行四层暴力循环，这样可以过70%，但是还有30%过不掉，这到题目甚至还让你暴力骗分了；

那么简单的暴力大家都会做，我们看看如何优化，这里用到的方法是前缀和加双指针，我们知道双指针就是用来优化n方到n，这样我们的枚举四层暴力循环就可以优化掉一重，那么如何写呢？

我们遍历i-j，内层遍历1-m，但是我们使用双指针遍历，这样复杂度就是三层，那么如何计算呢？

对于每一个r，我们计算从i到j的和，这里可以直接用前缀和计算，加入到我们的最大和sum中，当sum大于k时，我们就把l右移，直到sum小于k，每一次就都可以记录答案，答案数量为r-l+1，为什么是这个呢？，其实是从r往前计算的，r，r->r-1，r->r-2，....，r->l，总共r-l+1个区间和都是小于k的，也可以理解为从l出发到r，两种理解都一样，答案也一样，只不过对于过程理解不一样而已；

答案代码：

#include

using namespace std;
typedef long long LL;

int arr[510][510];

int main()
{
	int n,m,k;
	cin>>n>>m>>k;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
			cin>>arr[i][j];
			arr[i][j]+=arr[i-1][j];//我们只需要计算列上面的前缀和，行不用算 
		}
		
	LL ans=0;
	for(int i=1;i<=n;i++)
		for(int j=i;j<=n;j++)//循环行，用i，j循环 
			for(int l=1,r=1,p=0;r<=m;r++)//双指针循环列 
			{
				p+=arr[j][r]-arr[i-1][r];//这里p其实是sun，计算l到r，i到j的和； 
				while(p>k) 
				{
					p-=arr[j][l]-arr[i-1][l];//如果总和超过了k，就把左边的位置向右移 
					l++;
				}
				ans+=r-l+1;//记录答案 
			}
	cout<

五：积木画

题目链接：4406. 积木画 - AcWing题库

这道题目我想好多人第一眼看到的就想去找规律，我没找啊，因为我不会，但是呢，经过过后的学习，现在我已经掌握了这部分，那么让我来为大家解答；

首先不用说，肯定是个dp，其次我们发现他是一层层往后推的，那么我需要找到规律，经过分析之后，我们可以看到如下这个结论：

我们需要填满这一列，然后查看下一列的状态，这个时候我们发现如果填满这一列有好多种方法，但都会造成下一列状态的改变，所以这里我们需要把其他状态都列举出来，经过分析，我们有以下发现：

 

 

这是所有当前格子被涂的情况和他下一个格子的可能情况，这样我们就能知道某个格子她是从哪个格子转移过来，这样就可以计算了，我们把他们的形状定义为0-3，使用二进制表示，不涂为0，涂了下部分为1，涂了上部分为2，全涂为3，其实也是蒙德里安的梦想那道题目的表示；

接着我们可以使用一个二维数组，即可表示某个状态是否可以转移到另一个状态；

 我么会用左边一列代表上一个状态，用右边一列代表下一个状态，这样我们就可以进行计算了，如果上一个状态可以转移到下一个状态，我们就加上，如果不能就不用变；、

代码如下：

#include

using namespace std;

typedef long long LL;

int g[4][4]={
    {1,1,1,1,},
    {0,0,1,1,},
    {0,1,0,1,},
    {1,0,0,0,},
};//对应的转移所有状态 
const int mod=1000000007;

int ans[10000010][4];//这里如果不想使用大数组可以开个滚动数组 

int main()
{
	int n;
	cin>>n;
	ans[1][0]=1;//当只有一列答案为1 
	for(int i=1;i<=n;i++)//循环总长度 
		for(int j=0;j<4;j++)//循环在这个位置可能的四种情况 
		    for(int k=0;k<4;k++)//判断当上一个装为k时，能不能转移到这个状态 
		        ans[i+1][k]=(ans[i+1][k]+ans[i][j]*g[j][k])%mod;//这里判断的时下一个数组的情况，g数组存储能不能转移； 
	cout<

六：扫雷

题目链接：4407. 扫雷 - AcWing题库

这道题目不会写啊，因为之前没好好听离散化，所以这里就不会了，但是思路还是能和大家说说的；

这道题目我考场上是写出来了，方法用的没错，但是对于这道题目来说却不合适，我们看过题目就发现他其实是很简单的图论问题，就是直接炸一下，然后找到这个点的其他点一起炸，看着好像不难，数据太大了，用数组肯定不行，好多同学想到了建边，问题是他的雷有5e4，如果建边其实还好，毕竟数据范围在1e9，但是问题是，半径是10，如果把地雷集中一起填满，那么就有n*n条边大概是2e10，超时超空间；

就算你聪明进行判重，我们计算r=10，在半径范围内也有三百多个点，还可以开五百个，大概就是5千万条边，所以肯定过不去的，就别想着建边了，我当时用的是单链表，我开了1e7还是1e8忘了，反正是寄了；

顺便说一下，这个用单链表建边的思路出自蓝桥杯之前的一次题目叫做八数码，那道题目我使用了单链表来建边，也可以用并查集（不过我只会单链表，数据也不大，就过了）；

那么如何弄呢，答案是用散列表或者说是哈希表进行存储，然后直接暴力循环查找即可，这里只不过把循环边变成了暴力循环，做出来应该问题不大，我太笨不会写散列表，这道题就先寄着吧。

七：李白打酒加强版

题目链接：4408. 李白打酒加强版 - AcWing题库

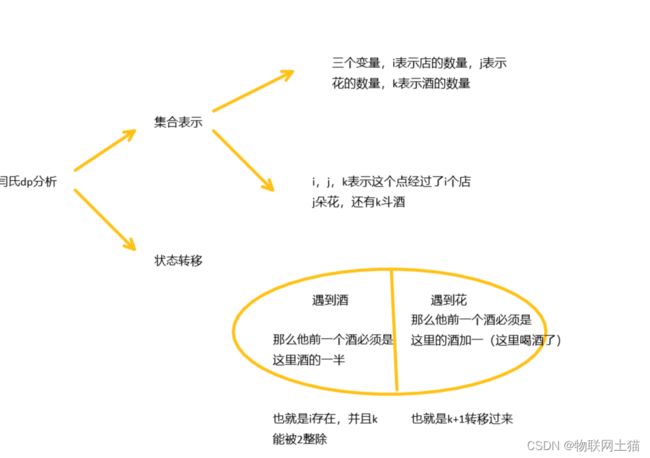
这是道典型的dp问题，相信大家一看到这道题目就知道得用dp，但是不会用（就像我一样，写个暴力搜索还没写出来...），这里给大家分析一下这道题目，这里我们使用闫氏dp分析法

经过分析之后，我们就可以根据分析写出代码了，注意这里的酒的数量其实是小于花的，因为他要保证酒要喝完，所以最后肯定不剩余，只要酒多于花，那么他的情况就都不会成立，

代码如下

#include

using namespace std;

const int mod=1000000007,N=110;
int arr[N][N][N];//店，酒，花的数量 

int main()
{
	int n,m;
	cin>>n>>m;
	
	arr[0][0][2]=1;//没店没花时应该是酒有两斗，直接结束 
	for(int i=0;i<=n;i++)//枚举店 
	{
		for(int j=0;j<=m;j++)//枚举花 
		{
			for(int k=0;k<=m;k++)//枚举酒 
			{
				if(i&&k%2==0) arr[i][j][k]=(arr[i][j][k]+arr[i-1][j][k/2])%mod;//遇到店
				//那么他不能是0，并且他的酒不能是奇数，因为遇到店就要加倍，不可能加倍后是奇数 
				if(j) arr[i][j][k]=(arr[i][j][k]+arr[i][j-1][k+1])%mod;//遇到花 
				//肯定有花，那么他的方案就是没有这朵花之前且没喝这一斗酒的方案数； 
			}
		}
	}
	cout<

八：砍竹子

y总讲了两种方法，但是没听懂第一种，第二种更容易理解，我也理所当然只听懂了第二种。

方法是：我们发现，如果它们处于同一高度就可以一起修剪，但是虽然最大到1e18，不超6次就变成1了，这个次数很少，我们如何去找到同一高度的竹子呢？

我们可以把所有数经过几步变成1存下来，因为n/2+1开根号能保证n与结果相差特别大，同时也最多也只会分解6个数，这时候我们就可以进行判断，如果这个数分解的某一步和前面的高度相同，那么这俩就可以在这个高度被剪掉，就算他们此时不在这个高度也没关系，也可以通过几次其他修剪到达这个高度，我们只需要判断这一步即可；

明白这个道理就很简单了，首先我们把数通过式子分解存储起来，这里我们要逆着存储，因为最后都会到0，但是最开始高度很分解的数的个数不一样；

接下来直接判断即可，

代码如下：

#include
#include
#include
#include
using namespace std;

typedef long long LL;
const int M=200010,N=10;
LL arr[M][N];
int main()
{
	int n;
	cin>>n;
	
	LL sta[10],top=0,mx=0,cnt=0;
	for(int i=0;i>p;
		while(p>1) sta[top++]=p,p=sqrt(p/2+1);//把这个数分解存储 
		mx=max(mx,top);//我们要找到最高的那个位置 
		cnt+=top;//一次剪一下，最大修剪次数 
		for(int j=0,k=top-1;k>=0;j++,k--)
		    arr[i][j]=sta[k];//把数的分解结果逆序存储进去 
	}
	for(int i=0;i

完结撒花