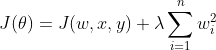【推荐收藏】三万字详解 TensorFlow 深度学习必备知识点（下）

各位同学好，之前跟大家分享了这篇: 【推荐收藏】三万字详解 TensorFlow 深度学习必备知识点（上）

今天我们继续讲 TensorFlow 深度学习必备知识点，目录如下：

解惑答疑

学了忘了、技术点不能吃透，可以加入技术交流，添加时最好的备注方式为：来源+兴趣方向，方便找到志同道合的朋友

方式①、添加微信号：mlc2060，备注：来自CSDN+加群
方式②、微信搜索公众号：机器学习社区，后台回复：加群

keras

主要内容有：

1.metrics指标
2.compile模型配置
3.fit模型训练
4.evaluate模型评估
5.predict预测
6.自定义网络

1、metrics 性能指标

加权平均值：tf.keras.metrics.Mean
预测值和真实值的准确度： tf.keras.metrics.Accuracy

1.1 新建一个 metrics 指标

准确度指标 metrics.Accuracy() 一般用于训练集，加权平均值 metrics.Mean() 一般用于测试集

# 新建准确度指标
acc_meter = metrics.Accuracy() 
# 新建平均值指标
mean_meter = metrics.Mean()  

1.2 向metrics添加数据

添加数据：update_state()。每一次迭代，都向准确率指标中添加测试数据的真实值和测试数据的预测值，将准确率保存在缓存区，需要时取出来。向平均损失指标中添加每一次训练产生的损失，每添加进来一个值就计算加权平均值，sample_weight指定每一项的权重，将结果保存在缓存区，需要时取出来。

# 计算真实值和预测值之间的准确度
acc_meter.update_state(y_true, predict) 
# 计算平均损失
mean_meter = mean_meter.update_state(loss, sample_weight=None)

1.3 从metrics中取出数据

取出数据：result().numpy()。result()返回tensor类型数据，转换成numpy()类型的数据。

# 取出准确率
acc_meter.result().numpy() 
# 取出训练集的损失值的均值
mean_meter.result().numpy()

1.4 清空缓存

清空缓存：reset_states()。每一次循环缓存区都会将之前的数据保存，在开始第二次循环之前，应该把缓存区清空，重新读入数据。

# 清空准确率的缓存
acc_meter.reset_states()
# 清空加权均值的缓存
mean_meter.reset_states()

2、compile 模型配置

compile(optimizer, loss, metrics, loss_weights)

参数设置：

optimizer： 用来配置模型的优化器，可以调用tf.keras.optimizers API配置模型所需要的优化器。

loss： 用来配置模型的损失函数，可以通过名称调用tf.losses API中已经定义好的loss函数。

metrics： 用来配置模型评价的方法，模型训练和测试过程中的度量指标，如accuracy、mse等

loss_weights： float类型，损失加权系数，总损失是所有损失的加权和，它的元素个数和模型的输出数量是1比1的关系。

# 选择优化器Adam，loss为交叉熵损失，测试集评价指标accurancy
network.compile(optimizer=optimizers.Adam(lr=0.01), #学习率0.01
    loss = tf.losses.CategoricalCrossentropy(from_logits=True),
    metrics = ['accuracy'])

---

3、fit 模型训练

fit(x, y, batch_size, epochs, validation_split, validation_data, shuffle,validation_freq)

参数：

x： 训练集的输入数据，可以是array或者tensor类型。

y： 训练集的目标数据，可以是array或者tensor类型。

batch_size： 每一个batch的大小，默认32

epochs： 迭代次数

validation_split： 配置测试集数据占训练数据集的比例，取值范围为0～1。

validation_data： 配置测试集数据(输入特征及目标)。如果已经配置validation_split参数，则可以不配置该参数。如果同时配置validation_split和validation_data参数，那么validation_split参数的配置将会失效。

shuffle： 配置是否随机打乱训练数据。当配置steps_per_epoch为None时，本参数的配置失效。

validation_freq： 每多少次循环做一次测试

# ds为包含输入特征及目标的数据集
network.fit(ds, eopchs=20, validation_data=ds_val, validation_freq=2)
# validation_data给定测试集，validation_freq每多少次大循环做一次测试，测试时自动计算准确率

---

4、evaluate 模型评估

evaluate(x, y, batch_size, sample_weight, steps)

返回模型的损失及准确率等相关指标

参数：

x： 输入测试集特征数据

y： 测试集的目标数据

batch_size： 整数或None。每个梯度更新的样本数。如果未指定，batch_size将默认为32。如果数据采用数据集，生成器形式，则不要指定batch_size。

sample_weight： 测试样本的可选Numpy权重数组，用于加权损失函数。

steps： 整数或None。宣布评估阶段结束之前的步骤总数。

5、predict 预测

predict(x, batch_size, steps)

参数：

x： numpy类型，tensor类型。预测所需的特征数据

batch_size： 每个梯度更新的样本数。如果未指定，batch_size将默认为32

steps： 整数或None，宣布预测回合完成之前的步骤总数（样本批次）。

等同于：

sample = next(iter(ds_pred)) # 每次从验证数据中取出一组batch
x = sample[0] # x 保存第0组验证集特征值
pred = network.predict(x)  # 获取每一个分类的预测结果
pred = tf.argmax(pred, axis=1) # 获取值最大的所在的下标即预测分类的结果
print(pred)

6、sequential

Sequential模型适用于简单堆叠网络层，即每一层只有一个输入和一个输出。

# ==1== 设置全连接层
# [b,784]=>[b,256]=>[b,128]=>[b,64]=>[b,32]=>[b,10]，中间层一般从大到小降维
network = Sequential([
    layers.Dense(256, activation='relu'), #第一个连接层，输出256个特征
    layers.Dense(128, activation='relu'), #第二个连接层
    layers.Dense(64, activation='relu'), #第三个连接层
    layers.Dense(32, activation='relu'), #第四个连接层
    layers.Dense(10), #最后一层不需要激活函数，输出10个分类
    ])
# ==2== 设置输入层维度
network.build(input_shape=[None, 28*28])
# ==3== 查看网络结构
network.summary()
# ==4== 查看网络的所有权重和偏置
network.trainable_variables
# ==5== 自动把x从第一层传到最后一层
network.call()

7、自定义层构建网络

通过对 tf.keras.Model 进行子类化并定义自己的前向传播模型。在 __init__ 方法中创建层并将它们设置为类实例的属性。在 call 方法中定义前向传播。

# 自定义Dense层
class MyDense(layers.Layer): #必须继承layers.Layer层，放到sequential容器中
    # 初始化方法
    def __int__(self, input_dim, output_dim):
        super(MyDense, self).__init__() # 调用母类初始化，必须
        
        # 自己发挥'w''b'指定名字没什么用，创建shape为[input_dim, output_dim的权重
        # 使用add_variable创建变量
        self.kernel = self.add_variable('w', [input_dim, output_dim])
        self.bias = self.add_variable('b', [output_dim])
    
    # call方法，training来指示现在是训练还是测试
    def call(self, inputs, training=None):
        out = inputs @ self.kernel + self.bias
        return out


# 自定义层来创建网络
class MyModel(keras.Model):  # 必须继承keras.Model大类，才能使用complie、fit等功能
    # 
    def __init__(self):
        super(MyModel, self).__init__() # 调用父类Mymodel
        # 使用自定义层创建5层
        self.fc1 = MyDense(28*28,256) #input_dim=784，output_dim=256
        self.fc2 = MyDense(256,128)
        self.fc3 = MyDense(128,64)
        self.fc4 = MyDense(64,32)
        self.fc5 = MyDense(32,10)

    def call(self, inputs, training=None):
        # x从输入层到输出层
        x = self.fc1(inputs)
        x = tf.nn.relu(x)
        x = self.fc2(x)
        x = tf.nn.relu(x)        
        x = self.fc3(x)
        x = tf.nn.relu(x)
        x = self.fc4(x)
        x = tf.nn.relu(x)
        x = self.fc5(x) #logits层
        return x

各位同学好，今天和大家分享一下TensorFlow2.0深度学习中的交叉验证法和正则化方法，最后展示一下自定义网络的小案例。

交叉验证、正则化，自定义网络

1、交叉验证

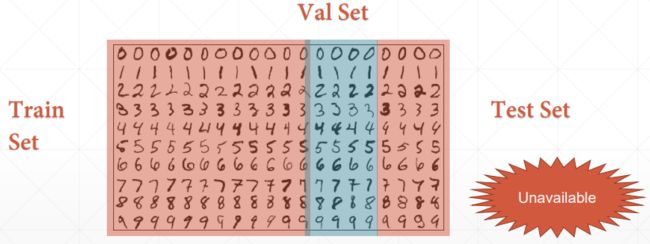
交叉验证主要防止模型过于复杂而引起的过拟合，找到使模型泛化能力最优的参数。我们将数据划分为训练集、验证集、测试集。训练集用于输入网络模型作为样本进行学习。验证集是在迭代过程中对模型进行评估，寻找最优解。测试集是在整个网络训练完成后进行评估。

K折交叉验证，就是将训练集数据等比例划分成K份，以其中的1份作为验证数据，其他的K-1份数据作为训练数据。每次迭代从都是从K个部分选取一份不同的数据部分作为测试数据，剩下的K-1个当作训练数据，最后把得到的K个实验结果进行平分。

​

​

划分方法

（1）构造数据集时划分

首先导入训练集(x,y)和测试集(x_test, y_test)，K折交叉验证是对测试集的划分，指定迭代500次，每次迭代都从训练集中选出一部分作为验证数据ds_val，剩下的作为训练数据ds_train。使用 tf.random.shuffle() 随机打乱索引顺序，不影响x和y之间的对应关系。tf.gather() 根据索引来选取值。

# 以手写数字为例，获取训练集和测试集
(x,y),(x_test,y_test) = datasets.mnist.load_data()

# 预处理函数
def processing(x,y): 
    # 从[0,255]=>[-1,1]
    x = 2 * tf.cast(x, dtype=tf.float32) / 255.0 - 1
    y = tf.cast(y, dtype=tf.int32)
    return(x,y)

# 交叉验证K=500
for epoch in range(500):

    idx = tf.range(60000) # 假设training数据一共有60k张图象，生成索引
    idx = tf.random.shuffle(idx) # 随机打乱索引
    
    # 利用随机打散的索引来收集数据，不改变xy之间的关联
    x_train, y_train = tf.gather(x, idx[:50000]), tf.gather(y, idx[:50000])
    x_val, y_val = tf.ga，ther(x, idx[-10000:]), tf.gather(y, idx[-10000:])
    
    # 构建训练集
    ds_train = tf.data.Dataset.from_tensor_slices((x_train, y_train))  # 自动将输入的xy转变成tenosr类型
    ds_train = ds_train.map(processing).shuffle(10000).batch(128) # 对数据集中的所有数据使用预处理函数
    
    # 构建验证集
    ds_val = tf.data.Dataset.from_tensor_slices((x_val, y_val))  
    ds_val = ds_test.map(processing).batch(128) # 每次迭代取128组数据，验证不需要打乱数据

（2）使用训练函数fit()中的参数划分

如果嫌使用上面的方法构造数据集太麻烦的话，可以在模型训练函数fit()中指定划分方式validation_split=0.1，每次迭代取0.1倍的训练数据作为验证集，剩下的作为训练集。ds_train_val 要求是没有被划分过的训练集数据。这样的话就不需要再指定validation_data验证集数据了，在划分时自动生成。

# ds_train_val指没有划分过的train和val数据集，validation_split=0.1动态切割，0.1比例的数据分给val
network.fit(ds_train_val, epochs=6, validation_split=0.1, validation_freq=2)
# 不需要再指定validation_data，已经在被包含在validation_split中了

在模型迭代过程中使用验证集来查看什么时候模型效果最优，找到最优的就跳出循环。验证集在挑选模型参数的时候，先保存误差极小值对应的权重，如果后面检测到的误差都大于它，就使用当前这个权重。

​

2、正则化

当采用比较复杂的模型，去拟合数据时，很容易出现过拟合现象，这会导致模型的泛化能力下降，对模型添加正则化项可以限制模型的复杂度，使得模型在复杂度和性能达到平衡。
​

L1正则化是在原来的损失函数基础上加上权重参数的绝对值。L1可以产生0解，L1获得稀疏解。

L2正则化是在原来的损失函数基础上加上权重参数的平方和。L2可以产生趋近0的解，L2获得非零稠密解。

在构建网络层时指定正则化参数kernel_regularizer，使用二范数的方法keras.regularizers.l2，惩罚系数0.01。

# 使用二范数正则化，loss = loss + 0.001*regularizer，指定正则化的权重
model = keras.Sequential([
    keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001), activation=tf.nn.relu),
    keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001), activation=tf.nn.relu),
    keras.layers.Dense(1, activation=tf.nn.sigmoid)])

3、自定义网络

3.1 数据获取

首先导入我们需要的库文件，从系统中导入图片数据，划分测试集和训练集。

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import datasets, layers, optimizers, Sequential, metrics
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # 输出框只输出有意义的信息

#（1）数据获取
(x,y),(x_test,y_test) = datasets.cifar10.load_data() #获取图像分类数据
# 查看数据信息
print(f'x.shape: {x.shape}, y.shape: {y.shape}')  #查看训练集的维度信息
print(f'x_test.shape: {x_test.shape}, y_test.shape: {y_test.shape}')  #测试集未读信息
print(f'y[:5]: {y[:5]}')  #查看训练集目标的前5项
# 绘图展示
import matplotlib.pyplot as plt
for i in range(10): # 展示前10张图片
    plt.subplot(2,5,i+1)  # 2行5列第i+1个位置
    plt.imshow(x[i])
    plt.xticks([]) # 不显示x和y轴坐标刻度
    plt.yticks([])

# 输入的图像形状
# x.shape: (50000, 32, 32, 3), y.shape: (50000, 1)
# x_test.shape: (10000, 32, 32, 3), y_test.shape: (10000, 1)

需要训练的图片如下，图片本身不清晰，这里只说一下基本的自定义网络的构造，最多只有80%准确率，模型优化到卷积神经网络章节再谈。

​

3.2 数据预处理

由于导入的目标值y的shape时二维[50k,1]，需要将axis=1的轴压缩掉，变成一个一维的向量[50k]，使用**tf.squeeze()**压缩指定轴，对目标值one-hot编码对应索引的值变为1，其他索引对应的值变为0，shape变为[b,10]。把特征值x的范围映射到[-1,1]之间。

#（2）数据预处理
# 定义预处理函数
def processing(x,y): 
    # 由于目标数据是而二维的，把shape=1的轴删除，从向量变成标量
    y = tf.squeeze(y)  # 默认压缩所有维度为1的轴，shape为[50k]
    y = tf.one_hot(y, depth=10) # one-hot编码，分成10个类别，shape为[50k,10]，对应下标所在的值为1
    # 每个像素值的范围在[-1,1]之间，从[0,255]=>[-1,1]
    x = 2 * tf.cast(x, dtype=tf.float32) / 255.0 - 1
    y = tf.cast(y, dtype=tf.int32)
    return(x,y)

# 构建训练集数据集
ds_train = tf.data.Dataset.from_tensor_slices((x, y))  # 自动将输入的xy转变成tenosr类型
ds_train = ds_train.map(processing).batch(128).shuffle(10000)  # 对数据集中的所有数据使用预处理函数

# 构建测试集数据集
ds_test = tf.data.Dataset.from_tensor_slices((x_test, y_test))  
ds_test = ds_test.map(processing).batch(128) # 每次迭代取128组数据，测试不需要打乱数据

# 构造迭代器，查看数据集是否正确
sample = next(iter(ds_train))  # 每次运行从训练数据集中取出一组xy
print('x_batch.shape', sample[0].shape, 'y_batch.shape', sample[1].shape)
# x_batch.shape (128, 32, 32, 3)   y_batch.shape (128, 10)

3.3 自定义网络

#（3）构造网络
class MyDense(layers.Layer): #必须继承layers.Layer层，放到sequential容器中
    # 代替layers.Dense层
    def __init__(self, input_dim, output_dim):
        super(MyDense, self).__init__()   # 调用母类初始化，必须

        # 自己发挥'w''b'指定名字没什么用，创建shape为[input_dim, output_dim的权重
        # 使用add_variable创建变量        
        self.kernel = self.add_variable('w',[input_dim, output_dim])
        self.bias = self.add_variable('b', [output_dim])

    # call方法，training来指示现在是训练还是测试         
    def call(self, inputs, training=None):
        
        x = inputs @ self.kernel + self.bias
        
        return x

# 自定义网络层
class MyNetwork(keras.Model):  # 必须继承keras.Model大类，才能使用complie、fit等功能
    
    def __init__(self):
        super(MyNetwork, self).__init__()  # 调用父类Mymodel
        # 新建五个层次
        self.fc1 = MyDense(32*32*3, 256)  #input_dim=784，output_dim=256
        self.fc2 = MyDense(256, 128)
        self.fc3 = MyDense(128, 64)
        self.fc4 = MyDense(64, 32)        
        self.fc5 = MyDense(32, 10)
  
    def call(self, inputs, training=None):
        # 前向传播，可以接收四维的tensor
        x = tf.reshape(inputs, [-1,32*32*3]) # 改变输入特征的形状
        x = self.fc1(x) #第一层[b,32*32*3]==>[b,256]
        x = tf.nn.relu(x) #激活函数
        x = self.fc2(x)
        x = tf.nn.relu(x)
        x = self.fc3(x)
        x = tf.nn.relu(x)
        x = self.fc4(x)
        x = tf.nn.relu(x)
        x = self.fc5(x)  #logits层
        return x

---

3.4 网络配置

#（4）网络配置
network = MyNetwork()       
network.compile(optimizer = optimizers.Adam(lr=0.001),  # 指定优化器
                loss = tf.losses.CategoricalCrossentropy(from_logits=True), #交叉熵损失
                metrics = ['accuracy'])  # 测试指标     

#（5）网络训练，输入训练数据，循环5次，验证集为ds_test，每一次大循环做一次测试
network.fit(ds_train, epochs=5, validation_data=ds_test, validation_freq=1)

# 循环5次后的结果为
Epoch 5/5
391/391 [==============================] - 3s 8ms/step - loss: 1.2197 - accuracy: 0.5707 - val_loss: 1.3929 - val_accuracy: 0.5182

学习率衰减策略

如何使用 TensorFlow 构建 多项式学习率衰减策略、单周期余弦退火学习率衰减策略、多周期余弦退火学习率衰减策略，并使用Mnist数据集来验证构建的方法是否可行。

下面创建的自定义学习率的类，都继承** tf.keras.optimizers.schedules.LearningRateSchedule

1、多项式衰减

1.1 方法介绍

学习率的多项式有两种情况，如下图所示。首先设置学习率的最高值和最低值，当学习率从最高点下降到最低点后。（1）cycle==False，接下去的所有学习率都保持最低值；（2）cycle==True，学习率从最低点上升到一个新的较高的值，并重新开始下降，以固定周期的形式，下降到最低点后又再次上升。

（1）cycle==False 的衰减公式

首先判断当前的 step 是否处于衰减周期 decay_period 中。如果在这个周期中，让用于计算的当前步数 current_step = step，表明学习率处于衰减过程之中；如果不在这个周期中，即已经下降到最低值，让用于计算当前步数 current_step = decay_period，表明已经结束了衰减过程。

计算公式如下：

lr 代表调整后的学习率；initial_lr 代表初始学习率，即最大学习率；min_lr 代表最小学习率；power 代表多项式的幂；其余同上

lr = (initial_lr - min_lr) * (1 - current_step / decay_period) ** (power) + min_lr

（2）cycle==True 的衰减公式

首先判断当前 step 处于第几个周期，计算公式如下。current_period 代表当前 step 处于第几个周期内；decay_period 代表一个衰减周期的 step 数；ceil 代表向上取整

current_period = decay_period * ceil(step / decay_period)

接下来就是计算衰减后的学习率，lr 代表调整后的学习率；initial_lr 代表初始学习率，即最大学习率；min_lr 代表最小学习率；power 代表多项式的幂

公式中的 step / current_period 一定是一个大于0小于1的数， 随着 step 增加，step越来越接近当前周期的step数，这一项就越来越接近1，那么整个 lr 就越来越接近0

lr = (initial_lr - min_lr) * (1 - step / current_period) ** (power) + min_lr

1.2 代码展示

这里的 cycle==True 衰减方式的计算，有一点和公式中不一样，在分母 current_period 后面增加了一项无限接近于0的数 keras.backend.epsilon()，防止分母为0，整个学习率变成无穷大。

lr = (initial_lr - min_lr) * (1 - step / (current_period + keras.backend.epsilon())) ** (power) + min_lr

我自定义的类，是继承至 keras.optimizers.schedules.LearningRateSchedule 自定义学习率调度器。为了清晰的展示训练过程中学习率的变化，如果当前的 step 是外部指定的 print_step 的整数倍，就打印一次学习率。并且使用列表 self.learning_rate_list 保存训练过程中每个 step 的学习率，训练完成之后，可调用查看。

# ----------------------------------------------------------------------- #
# 学习率多项式衰减
# ----------------------------------------------------------------------- #
# eager模式防止graph报错
tf.config.experimental_run_functions_eagerly(True)
# ----------------------------------------------------------------------- #
# 继承自定义学习率的类
class PolynomialDecay(keras.optimizers.schedules.LearningRateSchedule):
    '''
    initial_lr: 初始的学习率
    decay_period: 一次多项式衰减的周期
    power: 多项式的幂
    min_lr: 学习率的最小值
    cycle: 是否进行多个多项式衰减
    print_step: 训练时多少个step打印一次学习率
    '''
    # 初始化
    def __init__(self, initial_lr, decay_period, power, min_lr, cycle, print_step):
        # 继承父类的初始化方法
        super(PolynomialDecay, self).__init__()
        
        # 属性分配
        self.initial_lr = tf.cast(initial_lr, dtype=tf.float32)
        self.decay_period = tf.cast(decay_period, dtype=tf.float32)
        self.power = power
        self.min_lr = tf.cast(min_lr, dtype=tf.float32)
        self.cycle = cycle
        self.print_step = print_step
        
        # 保存每个step的学习率
        self.learning_rate_list = []
        
        
    # 前向传播
    def __call__(self, step):
        
        #（1）学习率达到最低学习率后，就一直保持最低学习率
        if self.cycle is False:
            
            # 比较找出当前step是否超出了一个周期
            current_step = tf.where(step<self.decay_period, step, self.decay_period)
            
            # 计算衰减后的学习率
            decayed_learning_rate = (self.initial_lr - self.min_lr) *                            \
                                    (1 - current_step / self.decay_period) ** (self.power) +     \
                                    self.min_lr
            
            # 保存每个step的学习率
            self.learning_rate_list.append(decayed_learning_rate.numpy().item())
                        
            # 训练时每个epoch打印一次学习率
            if step % self.print_step == 0:
                # 打印当前epoch的学习率
                print('learning_rate has changed to: ', decayed_learning_rate.numpy().item())
                
            # 返回调整后的学习率
            return decayed_learning_rate


        #（2）学习率达到最低后，再上升一个较高的学习率再下降
        if self.cycle is True:
            
            # 计算目前处于第几个周期, tf.math.ceil向上取整
            current_period = self.decay_period * tf.math.ceil(step / self.decay_period)
            
            # 计算衰减后的学习率, 分母加上一个很小的数keras.backend.epsilon()防止分母为0
            decayed_learning_rate = (self.initial_lr - self.min_lr) *                                \
                                    (1 - step / (current_period + keras.backend.epsilon())) **       \
                                    (self.power) + self.min_lr
            
            
            # 保存每个step的学习率
            self.learning_rate_list.append(decayed_learning_rate.numpy().item())
                        
            
            # 训练时每个epoch打印一次学习率
            if step % self.print_step == 0:
                # 打印当前epoch的学习率
                print('learning_rate has changed to: ', decayed_learning_rate.numpy().item())


            return decayed_learning_rate

---

2、单周期的余弦退火衰减

2.1 方法介绍

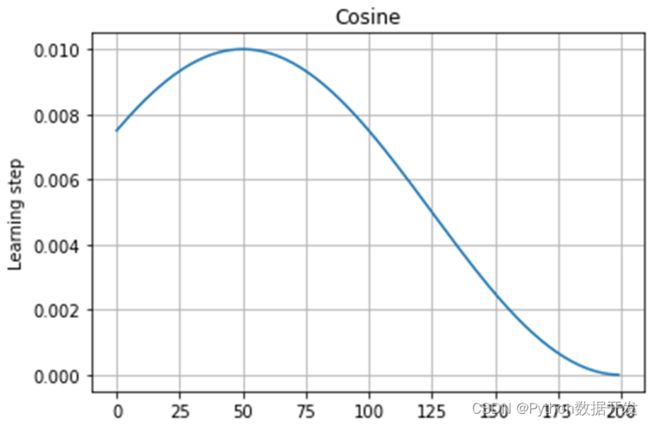
在传统的训练过程中，设置学习率的策略往往是阶梯式的或者指数衰减式的。若要是使用恒定的学习率进行训练，会使得模型在临近最优解的时候开始震荡，进而无法达到损失函数最低点的最优解。故而使用衰减的学习率，在靠近最优解的附近，梯度逐渐减小，对应减小学习率，使得模型能够顺利收敛到正确的期望位置。

然而在实际过程中，由于模型的复杂，很难正确的描述最优解位置以及损失函数的结构，这使得模型往往会收敛到一个局部的最优解。最终由于学习率的衰减，使得模型最终陷入一个局部的最优解，而非全局的最优解。

而对训练过程的学习率使用余弦退火方法则是通过不断的调整学习率，在衰减到一定值之后，重新调整恢复学习率，跳出当前的局部最优解而重新去寻找全局的最优解。

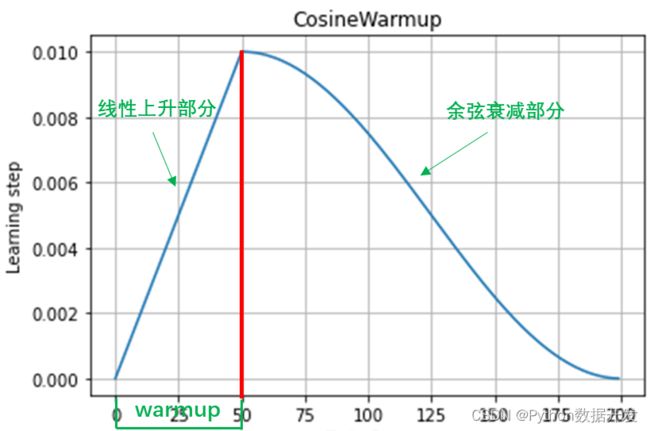
单周期余弦退火图像如下：

余弦曲线部分的计算公式如下，其中 initial_lr 代表最大学习率，min_lr 代表最小学习率，step_warmup 代表线性上升部分需要对step，total_step 代表一个周期的step

lr = min_lr + 0.5 * (initial_lr - min_lr) * (1 + cos(pi * (step-warmup_step) \ (total_step-warmup_step)))

该计算公式得出的结果在可视化后的曲线图如下，余弦曲线峰值点的位置就是线性上升部分的终点。

线性上升部分的计算公式如下，可理解为 y=kx+b 的形式。然后以 warmup 为界限，左侧为线性上升部分，右侧为余弦下降部分

# 增长系数k
k = (initial_lr - min_lr) / warmup_step 
# 增长线段 y=kx+b
warmup = k * step + min_lr

2.2 代码展示

重点的计算公式我已经在上面说明了，这里需要注意的就是 tf.where(step 这个函数的目的就是，如果当前step处于warmup阶段，那么就取线性部分，如果step超出了warmup阶段，就取余弦衰减部分。最终以warmup作为两种学习率的分界。

我自定义的类，是继承至 keras.optimizers.schedules.LearningRateSchedule 自定义学习率调度器。为了清晰的展示训练过程中学习率的变化，如果当前的 step 是外部指定的 print_step 的整数倍，就打印一次学习率。并且使用列表 self.learning_rate_list 保存训练过程中每个 step 的学习率，训练完成之后，可调用查看。

# ----------------------------------------------------------------------- #
# 单周期余弦退火衰减
# ----------------------------------------------------------------------- #
# eager模式防止graph报错
tf.config.experimental_run_functions_eagerly(True)
# ------------------------------------------------ #
import math

# 继承自定义学习率的类
class CosineWarmupDecay(keras.optimizers.schedules.LearningRateSchedule):
    '''
    initial_lr: 初始的学习率, 即最大学习率
    min_lr: 学习率的最小值
    warmup_step: 线性上升部分需要的step
    total_step: 整个余弦退火需要对总step
    print_step: 多少个step打印一次学习率
    '''
    # 初始化
    def __init__(self, initial_lr, min_lr, warmup_step, total_step, print_step):
        # 继承父类的初始化方法
        super(CosineWarmupDecay, self).__init__()
        
        # 属性分配
        self.initial_lr = tf.cast(initial_lr, dtype=tf.float32)
        self.min_lr = tf.cast(min_lr, dtype=tf.float32)
        self.warmup_step = warmup_step
        self.total_step = total_step
        self.print_step = print_step
        
        # 保存训练过程中每个step的学习率
        self.learning_rate_list = []
        
        
    # 前向传播
    def __call__(self, step):
        
        # 余弦曲线计算公式
        decayed_learning_rate = self.min_lr + 0.5 * (self.initial_lr - self.min_lr) *       \
                                (1 + tf.math.cos(math.pi * (step-self.warmup_step) /        \
                                 (self.total_step-self.warmup_step)))
        
        # 线性上升线段计算公式
        # 增长系数k
        k = (self.initial_lr - self.min_lr) / self.warmup_step 
        # 增长线段 y=kx+b
        warmup = k * step + self.min_lr
        
        # 将余弦部分和增长线段组合，以warmup_step为界限
        decayed_learning_rate = tf.where(step<self.warmup_step, warmup, decayed_learning_rate)
        
        # 保存每个step的学习率
        self.learning_rate_list.append(decayed_learning_rate.numpy().item())
        
        # 训练时每个epoch打印一次学习率
        if step % self.print_step == 0:
            # 打印当前epoch的学习率
            print('learning_rate has changed to: ', decayed_learning_rate.numpy().item())
    
        # 返回更新后的学习率
        return decayed_learning_rate

3、多周期余弦退火衰减

3.1 方法介绍

在看多周期之前，请先把上面的单周期掌握了。

这可以理解为是一种带重启的随机梯度下降算法。在网络模型更新时，由于存在很多局部最优解，这就导致模型会陷入局部最优解，即优化函数存在多个峰值。这就要求，当模型陷入局部最优解时，能够跳出去，并且继续寻找下一个最优解，直到找到全局最优解。要使得模型跳出局部最优解，就需要在模型陷入局部最优解时突然提高学习率，即重启学习率。

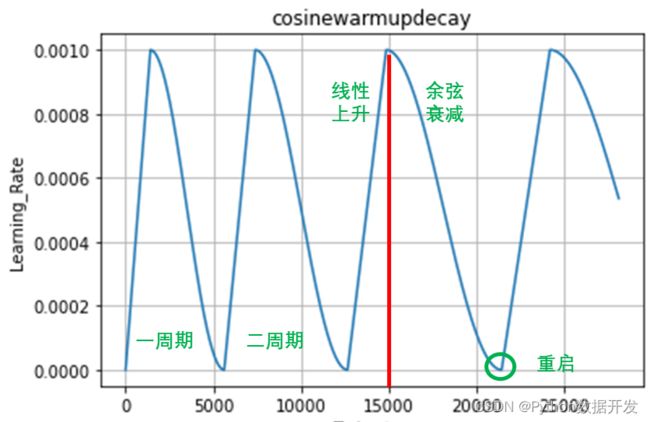
多周期的余弦退火衰减示意图如下：

多周期余弦退火算法的公式和单周期的一样，只需要在代码中稍做改动就可以了。改动的地方，新增了一个变量 self.step，并且在 __call__() 方法中，我增加了一个 if 条件判断。

我的思路是，如果当前的 step 到达了一个周期末尾的 step，那么就将当前 step 重置为 0，重新开始线性上升，并增加 warmup 段长度和整个周期的长度。如果有更好的方法，请大家在评论区指出来。

# ----------------------------------------------------------------------- #
# 多周期余弦退火衰减
# ----------------------------------------------------------------------- #
# eager模式防止graph报错
tf.config.experimental_run_functions_eagerly(True)
# ------------------------------------------------ #
import math

# 继承自定义学习率的类
class CosineWarmupDecay(keras.optimizers.schedules.LearningRateSchedule):
    '''
    initial_lr: 初始的学习率
    min_lr: 学习率的最小值
    max_lr: 学习率的最大值
    warmup_step: 线性上升部分需要的step
    total_step: 第一个余弦退火周期需要对总step
    multi: 下个周期相比于上个周期调整的倍率
    print_step: 多少个step并打印一次学习率
    '''
    # 初始化
    def __init__(self, initial_lr, min_lr, warmup_step, total_step, multi, print_step):
        # 继承父类的初始化方法
        super(CosineWarmupDecay, self).__init__()
        
        # 属性分配
        self.initial_lr = tf.cast(initial_lr, dtype=tf.float32)
        self.min_lr = tf.cast(min_lr, dtype=tf.float32)
        self.warmup_step = warmup_step  # 初始为第一个周期的线性段的step
        self.total_step = total_step    # 初始为第一个周期的总step
        self.multi = multi
        self.print_step = print_step
        
        # 保存每一个step的学习率
        self.learning_rate_list = []
        # 当前步长
        self.step = 0
        
        
    # 前向传播, 训练时传入当前step，但是上面已经定义了一个，这个step用不上
    def __call__(self, step):
        
        # 如果当前step达到了当前周期末端就调整
        if  self.step>=self.total_step:
            
            # 乘上倍率因子后会有小数，这里要注意
            # 调整一个周期中线性部分的step长度
            self.warmup_step = self.warmup_step * (1 + self.multi)
            # 调整一个周期的总step长度
            self.total_step = self.total_step * (1 + self.multi)
            
            # 重置step，从线性部分重新开始
            self.step = 0
            
        # 余弦部分的计算公式
        decayed_learning_rate = self.min_lr + 0.5 * (self.initial_lr - self.min_lr) *       \
                                (1 + tf.math.cos(math.pi * (self.step-self.warmup_step) /        \
                                  (self.total_step-self.warmup_step)))
        
        # 计算线性上升部分的增长系数k
        k = (self.initial_lr - self.min_lr) / self.warmup_step 
        # 线性增长线段 y=kx+b
        warmup = k * self.step + self.min_lr
        
        # 以学习率峰值点横坐标为界，左侧是线性上升，右侧是余弦下降
        decayed_learning_rate = tf.where(self.step<self.warmup_step, warmup, decayed_learning_rate)
        
        
        # 每个epoch打印一次学习率
        if step % self.print_step == 0:
            # 打印当前step的学习率
            print('learning_rate has changed to: ', decayed_learning_rate.numpy().item())
        
        # 每个step保存一次学习率
        self.learning_rate_list.append(decayed_learning_rate.numpy().item())

        # 计算完当前学习率后step加一用于下一次
        self.step = self.step + 1
        
        # 返回调整后的学习率
        return decayed_learning_rate

---

4、实践验证

下面以Mnist手写数据集为例，来验证一下上面定义的多周期余弦退火学习率衰减能不能用。预处理和网络构建我就不讲了，都比较基础，我们直接看到下面代码中的第（6）部分。

首先对我们自定义的学习率类实例化，传入必要的初始化参数 cosinewarmupdecay = CosineWarmupDecay(…)，然后将我们定义的学习率方法传入至Adam优化器中，keras.optimizers.Adam(cosinewarmupdecay)，那么在训练时，每次都会给这个类方法传入一个当前 step 值，经过计算学习率后，将调整后的学习率返回给模型。

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
import matplotlib.pyplot as plt

# 调用GPU加速
gpus = tf.config.experimental.list_physical_devices(device_type='GPU')
for gpu in gpus:
    tf.config.experimental.set_memory_growth(gpu, True)


# ----------------------------------------------------------------------- #
# （1）fashion_mnist数据预加载及预处理
# ----------------------------------------------------------------------- #
(x_train, y_train), (x_test, y_test) = keras.datasets.fashion_mnist.load_data()
print('x_train.shape:', x_train.shape, 'y_train.shape:', y_train.shape) # (60000, 28, 28) , (60000,)
print('x_test.shape:', x_test.shape)  # (10000, 28, 28)

# 记录训练集的数量
total_train_num = x_train.shape[0]


# ----------------------------------------------------------------------- #
# 学习率多周期余弦退火衰减
# ----------------------------------------------------------------------- #
# eager模式防止graph报错
tf.config.experimental_run_functions_eagerly(True)
# ------------------------------------------------ #
import math

# 继承自定义学习率的类
class CosineWarmupDecay(keras.optimizers.schedules.LearningRateSchedule):
    '''
    initial_lr: 初始的学习率
    min_lr: 学习率的最小值
    max_lr: 学习率的最大值
    warmup_step: 线性上升部分需要的step
    total_step: 第一个余弦退火周期需要对总step
    multi: 下个周期相比于上个周期调整的倍率
    print_step: 多少个step并打印一次学习率
    '''
    # 初始化
    def __init__(self, initial_lr, min_lr, warmup_step, total_step, multi, print_step):
        # 继承父类的初始化方法
        super(CosineWarmupDecay, self).__init__()
        
        # 属性分配
        self.initial_lr = tf.cast(initial_lr, dtype=tf.float32)
        self.min_lr = tf.cast(min_lr, dtype=tf.float32)
        self.warmup_step = warmup_step  # 初始为第一个周期的线性段的step
        self.total_step = total_step    # 初始为第一个周期的总step
        self.multi = multi
        self.print_step = print_step
        
        # 保存每一个step的学习率
        self.learning_rate_list = []
        # 当前步长
        self.step = 0
        
        
    # 前向传播, 训练时传入当前step，但是上面已经定义了一个，这个step用不上
    def __call__(self, step):
        
        # 如果当前step达到了当前周期末端就调整
        if  self.step>=self.total_step:
            
            # 乘上倍率因子后会有小数，这里要注意
            # 调整一个周期中线性部分的step长度
            self.warmup_step = self.warmup_step * (1 + self.multi)
            # 调整一个周期的总step长度
            self.total_step = self.total_step * (1 + self.multi)
            
            # 重置step，从线性部分重新开始
            self.step = 0
            
        # 余弦部分的计算公式
        decayed_learning_rate = self.min_lr + 0.5 * (self.initial_lr - self.min_lr) *       \
                                (1 + tf.math.cos(math.pi * (self.step-self.warmup_step) /        \
                                  (self.total_step-self.warmup_step)))
        
        # 计算线性上升部分的增长系数k
        k = (self.initial_lr - self.min_lr) / self.warmup_step 
        # 线性增长线段 y=kx+b
        warmup = k * self.step + self.min_lr
        
        # 以学习率峰值点横坐标为界，左侧是线性上升，右侧是余弦下降
        decayed_learning_rate = tf.where(self.step<self.warmup_step, warmup, decayed_learning_rate)
        
        
        # 每个epoch打印一次学习率
        if step % self.print_step == 0:
            # 打印当前step的学习率
            print('learning_rate has changed to: ', decayed_learning_rate.numpy().item())
        
        # 每个step保存一次学习率
        self.learning_rate_list.append(decayed_learning_rate.numpy().item())

        # 计算完当前学习率后step加一用于下一次
        self.step = self.step + 1
        
        # 返回调整后的学习率
        return decayed_learning_rate


# ----------------------------------------------------------------------- #
# （3）参数设置
# ----------------------------------------------------------------------- #
# 每个step处理多少张图像
batch_size = 32
# 迭代次数
num_epochs = 15
# 初始学习率
initial_lr = 0.001
# 学习率下降的最小值
min_lr = 1e-7
# 余弦退火的周期调整倍率
multi = 0.25

# 一个epoch包含多少个batch也是多少个steps, 即1875
one_epoch_batchs = int(total_train_num / batch_size)

# 第一个余弦退火周期需要的总step，以三个epoch为一个周期
total_step = one_epoch_batchs * 3

# 线性上升部分需要的step, 一个周期的四分之一的epoch用于线性上升
warmup_step = int(total_step * 0.25)

# 多少个step打印一次学习率, 一个epoch打印一次
print_step = one_epoch_batchs


# ----------------------------------------------------------------------- #
# （4）划分数据集
# ----------------------------------------------------------------------- #

# 预处理
def preprocessing(x, y):
    x = tf.cast(x, dtype=tf.float32) / 255.0  # 像素归一化
    x = tf.expand_dims(x, axis=-1)  # 增加通道维度
    y = tf.cast(y, dtype=tf.int32)  # 标签转为tensor类型
    return x,y

# 训练集
train_ds = tf.data.Dataset.from_tensor_slices((x_train, y_train)) 
train_ds = train_ds.map(preprocessing).batch(batch_size).shuffle(10000)
# 测试集
test_ds = tf.data.Dataset.from_tensor_slices((x_test, y_test))
test_ds = test_ds.map(preprocessing).batch(batch_size)

# 迭代器查看数据是否正确
sample = next(iter(train_ds))  
print('x_batch:', sample[0].shape, 'y_batch:', sample[1].shape)  # (32, 28, 28, 1), (32,)


# ----------------------------------------------------------------------- #
# （5）网络构建
# ----------------------------------------------------------------------- #
inputs = keras.Input(sample[0].shape[1:])  # 构造输入层
# [28,28,1]==>[28,28,32]
x = layers.Conv2D(32, kernel_size=3, padding='same', activation='relu')(inputs)
# [28,28,32]==>[14,14,32]
x = layers.MaxPool2D(pool_size=(2,2), strides=2, padding='same')(x)
# [14,14,32]==>[14,14,64]
x = layers.Conv2D(64, kernel_size=3, padding='same', activation='relu')(x)
# [14,14,64]==>[7,7,64]
x = layers.MaxPool2D(pool_size=(2,2), strides=2, padding='same')(x)
# [7,7,64]==>[None,7*7*64]
x = layers.Flatten()(x)
# [None,7*7*64]==>[None,128]
x = layers.Dense(128)(x)
# [None,128]==>[None,10]
outputs = layers.Dense(10, activation='softmax')(x)
# 构建模型
model = keras.Model(inputs, outputs)


# ------------------------------------------------------------------ #
# （6）模型训练
# ------------------------------------------------------------------ #
# 接收学习率调整方法
cosinewarmupdecay = CosineWarmupDecay(initial_lr=initial_lr, # 初始学习率，即最大学习率
                                  min_lr=min_lr,             # 学习率下降的最小值
                                  warmup_step=warmup_step,   # 线性上升部分的step
                                  total_step=total_step,     # 训练的总step
                                  multi=multi,               # 周期调整的倍率
                                  print_step=print_step)     # 每个epoch打印一次学习率值


# 设置adam优化器，指定学习率
opt = keras.optimizers.Adam(cosinewarmupdecay)

# 网络编译
model.compile(optimizer=opt,   # 学习率
              loss='sparse_categorical_crossentropy',  # 损失
              metrics=['accuracy'])  # 监控指标

# 网络训练
model.fit(train_ds, epochs=num_epochs, validation_data=test_ds)

# 绘制学习率变化曲线
plt.plot(cosinewarmupdecay.learning_rate_list)
plt.xlabel("Train step")
plt.ylabel("Learning_Rate")
plt.title('cosinewarmupdecay')
plt.grid()
plt.show()

我设置了在训练过程中，每个epoch打印一次学习率，训练过程如下：

Epoch 1/15
learning_rate has changed to:  1.0000000116860974e-07
1875/1875 [==============================] - 27s 14ms/step - loss: 0.9364 - accuracy: 0.6849 - val_loss: 0.3792 - val_accuracy: 0.8629
Epoch 2/15
learning_rate has changed to:  0.0009698210633359849
1875/1875 [==============================] - 25s 13ms/step - loss: 0.3030 - accuracy: 0.8920 - val_loss: 0.2907 - val_accuracy: 0.8989
------------------------------------------------------------
------------------------------------------------------------
Epoch 14/15
learning_rate has changed to:  0.0009987982921302319
1875/1875 [==============================] - 29s 15ms/step - loss: 0.1430 - accuracy: 0.9470 - val_loss: 0.2871 - val_accuracy: 0.9107
Epoch 15/15
learning_rate has changed to:  0.0008539927075617015
1875/1875 [==============================] - 29s 15ms/step - loss: 0.1213 - accuracy: 0.9563 - val_loss: 0.2902 - val_accuracy: 0.9156

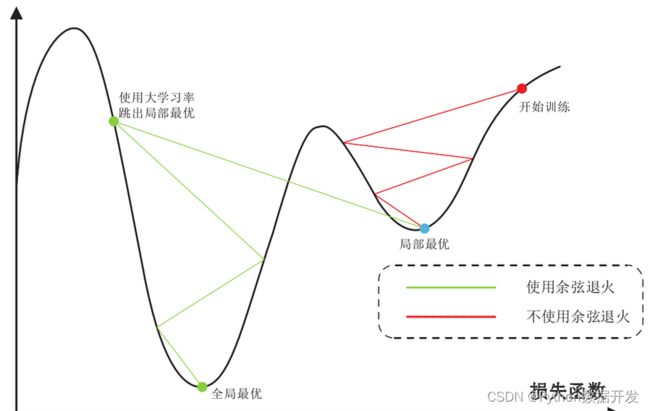
我设置了在训练过程中每一个step都保存一次当前学习率值，保存于 self.learning_rate_list ，训练完成之后可以通过 cosinewarmupdecay.learning_rate_list 读取这个列表，绘制学习率变化曲线

使用余弦退火学习率衰减方法和传统的学习率连续衰减方法的对比图