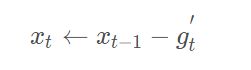深度学习Optimizer优化器小结

禁止任何形式的转载!!!

简介

目前各类采用梯度下降进行更新权重的优化算法无非就是对下面公式三个红框部分进行不断改进。

现在深度学习所用的优化器大多可以划分为两大类：

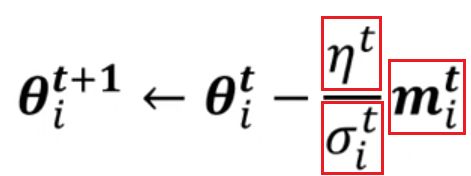
代码

torch.optim包里实现了实现各种常用的优化算法，使用时先建立优化器对象
optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9)，当想要指定每层学习速率时：

optim.SGD([
                {'params': model.base.parameters()},
                {'params': model.classifier.parameters(), 'lr': 1e-3}#学习率1e-3 动量0.9
            ], lr=1e-2, momentum=0.9) #除了特别设置参数，默认都使用学习率1e-2 动量0.9

使用示例：

for input, target in dataset:
    optimizer.zero_grad() #先要将之前的梯度清零，才反向传播计算新的梯度
    output = model(input)
    loss = loss_fn(output, target)
    loss.backward()
    optimizer.step() #参数进行一次更新

优化器算法介绍

1.SGD

带动量的随机梯度下降SGDM是最常用的方法

torch.optim.SGD(params, lr=xxx, momentum=0, dampening=0, weight_decay=0, nesterov=False)

参数含义：假设g为梯度，p为参数
momentum动量：即μ （默认0 常用0.9）
weight_decay权重衰减：L2正则化

dampening抑制因子：是乘到g上的一个数，(1-dampening)*g_t+1
nesterov:牛顿动量法是Momentum的进一步变形，Momentum动量是在原位置计算梯度之后更新，Nesterov牛顿动量是先将动量加上在新位置计算梯度后进行修正更新。(即NAG)

momentum首先计算一个梯度(短的蓝色向量)，然后在加速更新梯度的方向进行一个大的跳跃(长的蓝色向量)，nesterov项首先在之前加速的梯度方向进行一个大的跳跃(棕色向量)，计算梯度然后进行校正(绿色梯向量)

SGD的特点：由于积累之前的动量来替代真正的梯度，下降初期时，使用上一次参数更新，下降方向一致，乘上较大的μ能够进行很好的加速。在梯度方向发生改变时，μ能减少更新，抑制振荡，从而加快收敛。

2.Adagrad

自适应梯度算法是为了自适应调整学习率，给学习率加上了一项分母。

torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0, initial_accumulator_value=0, eps=1e-10)

特点：学习率随着梯度值的累加而变小，起到了学习率减少的作用；中后期由于分母的累积会使得学习率很小，可能使得训练提前结束。（较少使用）

3.RMSprop

torch.optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)

由于Adagrad一直累加之前的所有梯度，使得学习率之后很小，且受全局的梯度影响。RMSprop这里进行了改进，分母虽然是累加但是经过了指数加权移动平均，可以看作只受最近的梯度影响。

特点：训练初中期，加速效果不错，很快训练，后期，梯度小学习率变大，可能会反复在局部最小值附近抖动，也可能跳出局部最小值找到更好的解。

3.Adadelta

torch.optim.Adadelta(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)

AdaDelta算法也像RMSProp算法一样

与RMSProp算法不同的是，AdaDelta算法还维护一个额外的状态变量Δx

AdaDelta算法没有学习率超参数，它通过使用有关自变量更新量平方的指数加权移动平均的项来替代RMSProp算法中的学习率。

5.Adam

torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)

Adam是RMSProp的动量版，原来的梯度变成带动量的梯度，此外还为了消除刚开始没有梯度累计时的偏差，除了一项随时间变大的式子。


由表达式可以看出，对更新的步长计算，能够从梯度均值及梯度平方两个角度进行自适应地调节，而不是直接由当前梯度决定。β₂=0.999意味着分母会综合1000步的梯度平方。缺点：当训练到后期的时候，梯度通常都是很小的，少量有用的大梯度会被大量无用的梯度淹没

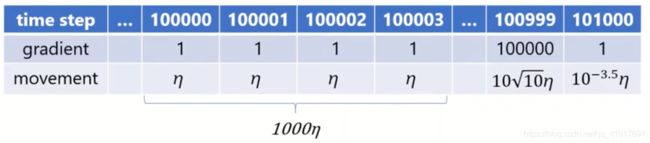
所以有人提出了amsgrad：但是这样又会使得分母越来越大，出现早停

此外，有人在使用Adam的时候将lr打印出来发现后期学习率会比较极端，量级相差较大。

有人就进行了Clip，但是感觉完全是凭经验设计的，一点也不adaptive

6.Adamax

torch.optim.Adamax(params, lr=0.002, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)

Adamax是Adam的一种变体，此方法对分母部分进行了改进，Adam单个权重的更新规则是将其梯度与当前和过去梯度的L2范数成反比例缩放，这里泛化到基于Lp范数的更新规则，虽然p的值较大会使得数值上变得不稳定，但令p趋于无穷会得出一个稳定和简单的算法。经过推导，分母的更新变成了max（），增加了一个学习率上限的概念，与原来的g_t²不同。与AMSgrad有一定相似之处。

7.NAdam

torch.optim.NAdam(params, lr=0.002, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, momentum_decay=0.004)

NAdam是将Nesterov NAG的思想用到了Adam上

8.RAdam

torch.optim.RAdam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)

将warmup的思想用到ADAM上

9.AdamW*

torch.optim.AdamW(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0.01, amsgrad=False)

AdamW是在Adam+L2正则化的基础上进行改进的算法
这是因为，后来有学者认为Adam算法存在错误，本来正则化是对权重参数进行约束的，但是在SGDM Adam加入动量后一并将正则化引入到动量和分母之中。

因此后面提出AdamW，正则化只在参数更新的时候用到，这个在某些Bert训练中得到了运用。

所以，注意区分L2 penalty 与weight decay，下面两图分别是Adam与AdamW参数的解释，可见在优化器里着两者有着不同的含义。

其它

小结

就我个人而言，喜欢使用SGD搭配learning rate schedules，通过多次实验找到一个适合模型训练的学习率和策略，一般来说在验证集的精度上要比Adam要好一点。不过，在合适的初始化和优化器下，不同优化器给模型带来的提升其实并不大，可以多花时间在其它地方进行优化。

请看下一个息息相关的小结:learning rate schedules总结

目前较为出名的模型，YOLO、MaskRCNN、ResNet等都采用SGDM，Transformer、Bert、Big-GAN、MEMO等都采用的Adam。

禁止任何形式的转载!!!