基于MATLAB_GUI的发动机曲柄活塞铰链四杆机构优化设计与仿真

目录
摘要 I
Abstract II
第一章绪论 1
1.1 机构学的概念与发展 1
1.1.1机构学的概念与地位 1
1.1.2 机构学的发展与成果 1
1.1.3 机构学的未来 3
1.2 MATLAB的介绍 3
1.2.1 MATLAB的基础功能 3
1.2.2 MATLAB的优化 4
1.3 课题介绍和内容安排 5
第二章连杆机构常用设计方法 6
2.1 连杆机构的介绍 6
2.2 连杆机构的设计方法 7
2.2.1 图解法 7
2.2.2 解析法 7
2.3 连杆机构的优化方法 8
2.3.1 优化函数的含义 8
2.3.2 优化函数的使用 8
第三章铰链四杆机构的设计 10
3.1 铰链四杆机构的常规设计 10
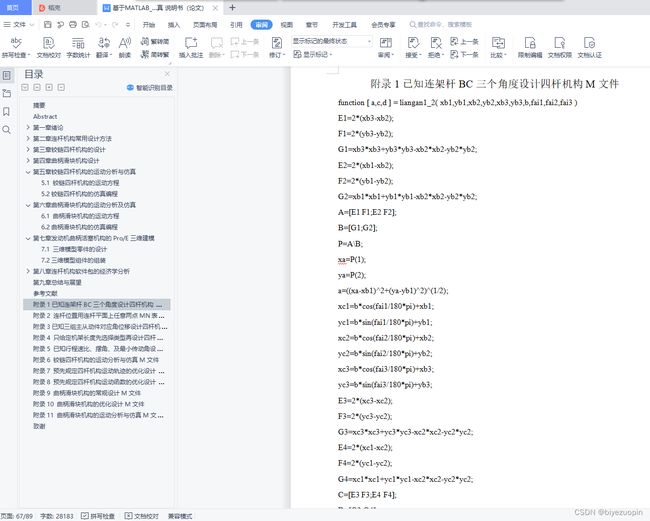
3.1.1 已知连架杆BC三个角度设计四杆机构 10
3.1.2 连杆位置用连杆平面上任意两点MN表示设计四杆机构 14
3.1.3 已知三组主从动件对应角位移设计四杆机构 17
3.1.4 只给定机架长度先选择类型再设计四杆结构 21
3.1.5 已知行程速比、摆角、及最小传动角设计四杆结构 25
3.2 铰链四杆机构的优化设计 28
3.2.1 预先规定四杆机构运动轨迹的优化设计 28
3.2.2 预先规定连杆运动函数的优化设计 33
第四章曲柄滑块机构设计 39
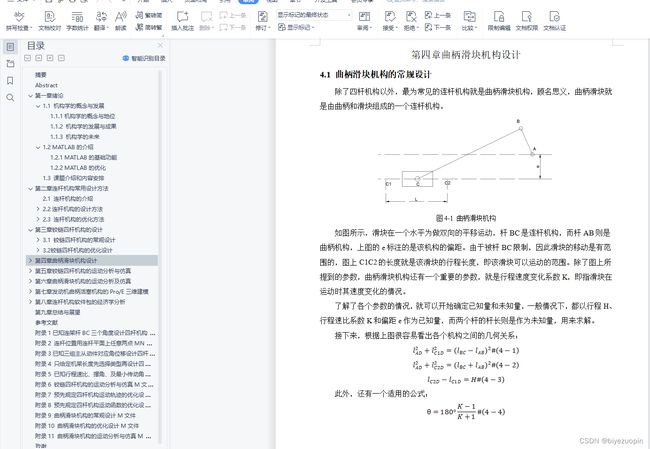
4.1 曲柄滑块机构的常规设计 39
4.2 曲柄滑块机构的优化设计 41
第五章铰链四杆机构的运动分析与仿真 44
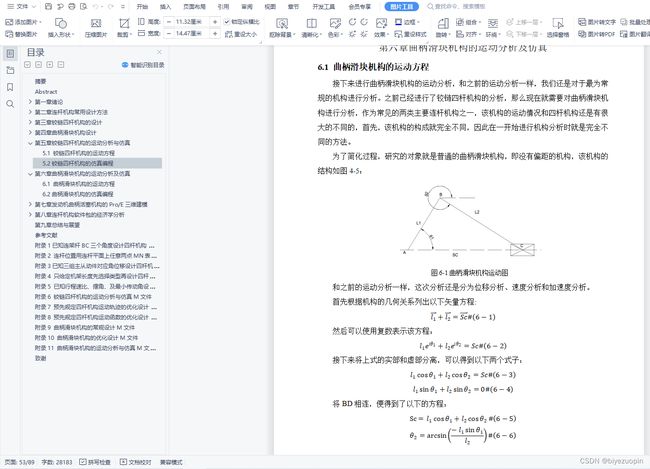
5.1 铰链四杆机构的运动方程 44
5.2 铰链四杆机构的仿真编程 45
第六章曲柄滑块机构的运动分析及仿真 47
6.1 曲柄滑块机构的运动方程 47
6.2 曲柄滑块机构的仿真编程 48
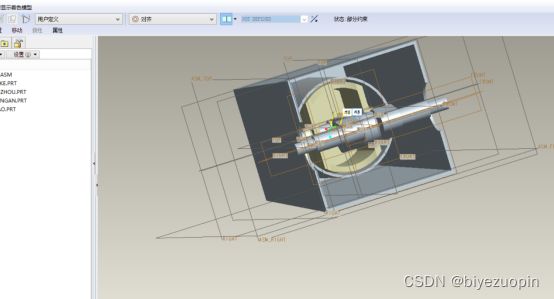
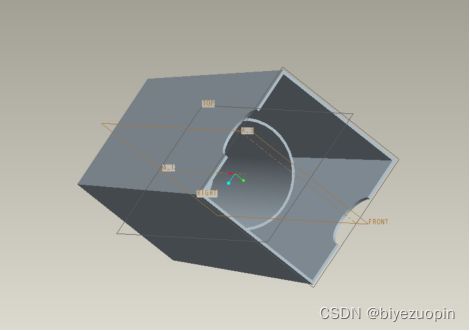
第七章发动机曲柄活塞机构的Pro/E三维建模 50
7.1 三维模型零件的设计 50
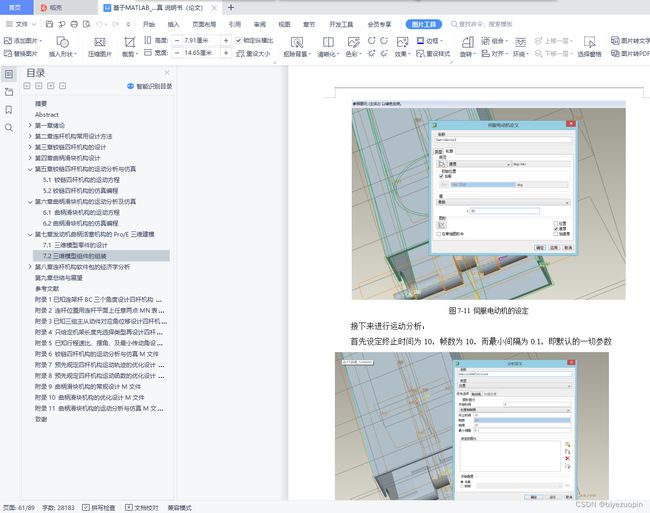
7.2 三维模型组件的组装 52
第八章连杆机构软件包的经济学分析 56
8.1 连杆机构软件市场分析 56
8.2 连杆机构包成本核算 57
第九章总结与展望 58
参考文献 60
附录1 已知连架杆BC三个角度设计四杆机构M文件 62
附录2 连杆位置用连杆平面上任意两点MN表示设计四杆机构M文件 64
附录3 已知三组主从动件对应角位移设计四杆机构M文件 65
附录4 只给定机架长度先选择类型再设计四杆结构M文件 66
附录5 已知行程速比、摆角、及最小传动角设计四杆结构M文件 71
附录6 铰链四杆机构的运动分析与仿真M文件 72
附录7 预先规定四杆机构运动轨迹的优化设计M文件 75
附录8 预先规定四杆机构运动函数的优化设计M文件 77
附录9 曲柄滑块机构的常规设计M文件 79
附录10 曲柄滑块机构的优化设计M文件 80
附录11 曲柄滑块机构的运动分析与仿真M文件 81
致谢 84
连杆作为机构中最为常见的一类，在生产中时常都会用到连杆，因此连杆的研究问题就成了一个不可回避的紧迫问题。因此，本课题着重对于连杆的设计和优化进行了一系列分类研究，力求在绝大部分情况下都可以找到一个合适的连杆解决方案。关于连杆问题的设计优化，采取的思想是根据已知条件进行分类研究，再使用MATLAB软件进行数学模型的设计优化处理。一般连杆问题可以分为大致六类，以下会逐一地专门介绍，而连杆的优化问题，着重研究三类。
本文的内容安排如下：
（1）对于铰链四杆模型和曲柄滑块模型进行数学模型的分析；
（2）使用 MATLAB根据分析出的数学模型对各类情况逐个进行程序的编程；
（3）使用MATLAB绘制四杆机构和曲柄滑块机构的运动仿真图；
（4）使用MATLBA对各个程序编写相应的GUI界面；
（5）使用Pro-E软件绘制连杆三维模型；
3.2铰链四杆机构的优化设计
3.2.1 预先规定四杆机构运动轨迹的优化设计
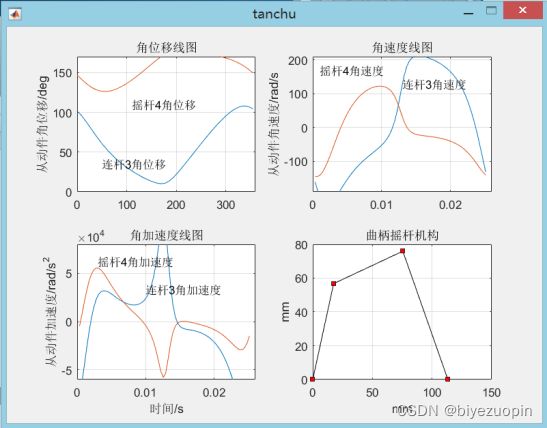
连杆机构的优化设计主要分为两类，其中第一类，即实现连杆预定轨迹的优化设计。这类设计设计连杆机构的依据是该连杆机构运动的轨迹，即让连杆上一点按照给定的轨迹运动，由于连杆机构上任意一点有且只有一条运动轨迹，且该轨迹只能适合一个机构的运动，因此，只需要确定一个点的运动轨迹便可以确定该机构的各杆情况。
如下图所示，可以清晰地看到M点的轨迹变化，因此，就预先设定BC杆上一点M的轨迹。但是稍微分析一下，就能发现M点的变化应该是一个光滑的曲线，因此，需要给出的轨迹应该是一个可以表示M点运动的函数，但是这很难实现，所以便优先给定大量的M点，近似地进行轨迹的安排。如果给出的轨迹是近似的，这在设计的时候便会出现一定的误差，因此就可以在此基础上进行优化，以求让实际运动的轨迹和给定的轨迹之间的误差最小。

图3-22M点预定的轨迹图

l1=30;
l2=75;
omega1=40;
theta1=0;
for i=1:161
thate2=asin((-1*l1*sin(theta1/180*pi))/l2)/pi*180;
sc=l1*cos(theta1/180*pi)+l2*cos(thate2/180*pi);
th34(i,:)=[theta1 thate2 sc];
theta1=theta1+5;
end
subplot(2,2,1);
[AX1]=plotyy(th34(:,1),th34(:,2),th34(:,1),th34(:,3));
grid ;
title('位移线图');
xlabel('曲柄转角θ/°');
set(get(AX1(1),'Ylabel'),'String','连杆角位移/°');
set(get(AX1(2),'Ylabel'),'String','滑块位移/mm');
for i=1:161
f1=l2*sin(th34(i,2)/180*pi);
f2=1;
g1=-1*l2*cos(th34(i,2)/180*pi);
g2=0;
h1=-1*l1*sin(th34(i,1)/180*pi)*omega1;
h2=l1*cos(th34(i,1)/180*pi)*omega1;
A=[f1 f2;g1 g2];
B=[h1;h2];
P=A\B;
omega2=P(1);
vc=P(2);
om34(i,:)=[th34(i,1) omega2 vc];
end
subplot(2,2,2);
[AX2]=plotyy(om34(:,1),om34(:,2),om34(:,1),om34(:,3));
grid ;
title('速度线图');
xlabel('曲柄转角θ/°');
set(get(AX2(1),'Ylabel'),'String','连杆角速度/rad/s');
set(get(AX2(2),'Ylabel'),'String','滑块速度/mm/s');
for i=1:161
f3=l2*sin(th34(i,2)/180*pi);
f4=1;
g3=-1*l2*cos(th34(i,2)/180*pi);
g4=0;
h3=-1*l1*cos(th34(i,1)/180*pi)*omega1*omega1-l2*cos(th34(i,2)/180*pi)*om34(i,2)*om34(i,2);
h4=-1*l1*sin(th34(i,1)/180*pi)*omega1*omega1-l2*sin(th34(i,2)/180*pi)*om34(i,2)*om34(i,2);
C=[f3 f4;g3 g4];
D=[h3;h4];
Q=C\D;
alpha2=Q(1);
ac=Q(2);
js34(i,:)=[th34(i,1) alpha2 ac];
end
subplot(2,2,3);
[AX3]=plotyy(js34(:,1),js34(:,2),js34(:,1),js34(:,3));
grid ;
title('加速度线图');
xlabel('曲柄转角θ/°');
set(get(AX3(1),'Ylabel'),'String','连杆角加速度/rad/(s*s)');
set(get(AX3(2),'Ylabel'),'String','滑块加速度/mm/(s*s)');

% syms omega2 vc
% f1=l2*sin(thate2/180*pi);
% f2=1;
% g1=-1*l2*cos(thate2/180*pi);
% g2=0;
% h1=-1*l1*sin(theta1/180*pi)*omega1;
% h2=l1*cos(theta1/180*pi)*omega1;
% A=[f1 f2;g1 g2];
% B=[h1;h2];
% P=A\B;
% omega2=P(1);
% vc=P(2);
% om34(i,:)=[i omega2 vc];
% f3=l2*sin(thate2/180*pi);
% f4=1;
% g3=-1*l2*cos(thate2/180*pi);
% g4=0;
% h3=-1*l1*cos(theta1/180*pi)*omega1*omega1-l2*cos(thate2/180*pi)*omega2*omega2;
% h4=-1*l1*sin(theta1/180*pi)*omega1*omega1-l2*sin(thate2/180*pi)*omega2*omega2;
% C=[f3 f4;g3 g4];
% D=[h3;h4];
% Q=C\D;
% alpha2=Q(1,:);
% ac=Q(2,:);
% subplot(2,2,1);
% plotyy(theta1,thate2,theta1,sc);
% hold on;
% subplot(2,2,3);
% plotyy(theta1,alpha2,theta1,ac);
% hold on;