神经网络训练梯度算法详解
文章目录
- 题目
- The basic definition
- The motivation
- Paper detailed introduction
-
- 梯度下降变体
-
- 批梯度下降
- 随机梯度下降算法
- 小批量梯度下降法MBGD
- Challenges
- Gradient descent optimization algorithms
-
- Momentum
- Nesterov accelerated gradient
- AdaGrad
- RMSProp
- Adadelta
- Adam
- Nadam and Adammax
- 对比图
- 总结
- Which optimizer to use
- Parallelizing and distributing SGD
-
- Hogwild
- Downpour SGD
- Delay-tolerant Algorithms for SGD
- TensorFlow
- Elastic A veraging SGD
- Additional strategies for optimizing SGD
-
- Shuffling and Curriculum Learning
- Batch normalization
- Early stopping
题目
- An overview of gradient descent optimization
The basic definition
-
鞍点：一个维度向上倾斜且另一维度向下倾斜的点。这些鞍点通常被相同误差值的平面所包围，这使得算法陷入其中很难脱离出来，因为梯度在所有维度上接近于零。
-
一篇论文《Identifying and attacking the saddle point problem in high-dimensional non-convex optimization》参考，提出高维非凸优化问题之所以困难，是因为存在大量的鞍点而不是局部极值。
-
鞍点和局部极值的区别：
f ( x + η u ) ≈ f ( x ) + η 2 2 u ⊤ ∇ 2 f ( x ) u > f ( x ) f(x+\eta u) \approx f(x)+\frac{\eta^{2}}{2} u^{\top} \nabla^{2} f(x) u>f(x) f(x+ηu)≈f(x)+2η2u⊤∇2f(x)u>f(x)
当Hessian矩阵正定时（即对任意的u≠0，有 u T ∇ 2 f ( x ) u > 0 u^{T}∇2f(x)u > 0 uT∇2f(x)u>0恒成立），对于任何方向向量u，通过二阶泰勒展开式，可知x必定是一个局部最小值点。同样，当Hessian矩阵负定时，此点是一个局部最大值点；当Hessian矩阵同时具有正负特征值时，此点便是鞍点。(有时候可以更进二阶导数，若某个一阶导数为0的点在至少一个方向上的二阶导数小于0，那它就是鞍点)- 鞍点和局部极小值相同的是，在该点处的梯度都等于零，不同在于在鞍点附近Hessian矩阵是不定的(行列式小于0)，而在局部极值附近的Hessian矩阵是正定的。
- 在鞍点附近，基于梯度的优化算法（几乎目前所有的实际使用的优化算法都是基于梯度的）会遇到较为严重的问题：
- 鞍点处的梯度为零，鞍点通常被相同误差值的平面所包围（这个平面又叫Plateaus，Plateaus是梯度接近于零的平缓区域，会降低神经网络学习速度），在高维的情形，这个鞍点附近的平坦区域范围可能非常大，这使得SGD算法很难脱离区域，即可能会长时间卡在该点附近（因为梯度在所有维度上接近于零）。
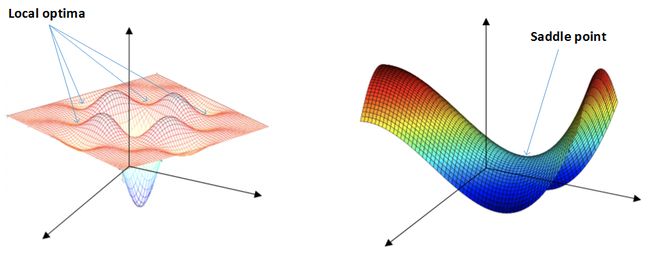
- 图一表示：神经网络只有两个参数时的情况（水平方向分别为两个参数，纵轴代表损失函数），有多个局部最小值
图二表示：神经网络具有高维参数时，可看到有鞍点。
-
-
Plateaus是梯度接近于零的平缓区域，会降低神经网络学习速度
The motivation
- 梯度下降优化算法虽然越来越流行，但经常被用作黑盒优化器，因为很难对它们的优缺点进行实用的解释
- 本文旨在为读者提供有关不同算法的想法，使他们可以使用它们
- 研究了梯度下降的不同变体，总结了各种挑战，介绍了最常用的优化算法，在并行和分布式环境中查看了架构，并研究了用于优化梯度下降的其他策略
Paper detailed introduction
梯度下降变体
批梯度下降
θ = θ − η ⋅ ∇ θ J ( θ ; x ( i ) ; y ( i ) ) \theta=\theta-\eta \cdot \nabla_{\theta} J\left(\theta ; x^{(i)} ; y^{(i)}\right) θ=θ−η⋅∇θJ(θ;x(i);y(i))
- 我们在训练神经网络模型时，最常用的就是梯度下降，批梯度下降，BGD，一次迭代训练所有样本
- BGD的优点是理想状态下经过足够多的迭代后可以达到全局最优。但是缺点也很明显，就是如果你的数据集非常的大（现在很常见），根本没法全部塞到内存（显存）里，所以BGD对于小样本还行，大数据集就没法娱乐的玩耍了。而且因为每次迭代都要计算全部的样本，所以对于大数据量会非常的慢。
随机梯度下降算法
θ = θ − η ⋅ ∇ θ J ( θ ; x ( i ) ; y ( i ) ) \theta=\theta-\eta \cdot \nabla_{\theta} J\left(\theta ; x^{(i)} ; y^{(i)}\right) θ=θ−η⋅∇θJ(θ;x(i);y(i))
-
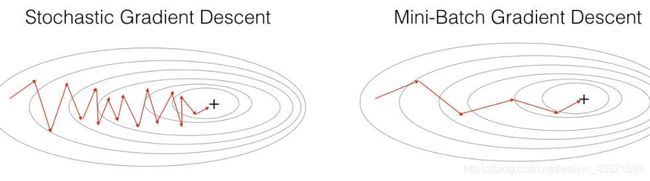
为了加快收敛速度，并且解决大数据量无法一次性塞入内存（显存）的问题，SGD就被提出来了，SGD的思想是每次只训练一个样本去更新参数。
-
SGD优缺点
- 因为每次只用一个样本来更新参数，会导致不稳定性大些，每次仅仅用一个样本去去决定梯度方向，往往得到解可能不是最优解。由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。
- 每次训练用一个样本所以训练速度快
小批量梯度下降法MBGD
θ = θ − η ⋅ ∇ θ J ( θ ; x ( i : i + n ) ; y ( i : i + n ) ) \theta=\theta-\eta \cdot \nabla_{\theta} J\left(\theta ; x^{(i: i+n)} ; y^{(i: i+n)}\right) θ=θ−η⋅∇θJ(θ;x(i:i+n);y(i:i+n))
- 在上述的批梯度的方式中每次迭代都要使用到所有的样本，对于数据量特别大的情况，如大规模的机器学习应用，每次迭代求解所有样本需要花费大量的计算成本。是否可以在每次的迭代过程中利用部分样本代替所有的样本呢？基于这样的思想，便出现了mini-batch的概念。这种方法是前两种方法的折中。现在深度学习中，基本上都是用 mini-batch gradient descent，（在深度学习中，很多直接把mini-batch gradient descent（a.k.a stochastic mini-batch gradient descent）简称为SGD，所以当你看到深度学习中的SGD，一般指的就是mini-batch gradient descent）
Challenges
小批量梯度下降不能保证良好的收敛性，但是会带来一些需要解决的挑战
- 选择合适的学习率可能很困难。学习率太小会导致收敛缓慢而痛苦，而学习率太大会阻碍收敛，并导致损失函数在最小值附近波动甚至发散。因为小样本有很大的随机性，小样本的梯度不能指示参数优化的大方向。
- 学习率策略试图通过例如调整训练过程中的学习率,根据预定义的策略或在各个时期之间的目标变化低于阈值时降低学习率，但是，这些计划和阈值必须预先定义，因此无法适应数据集的特征
- 相同的学习率适用于所有的参数更新，如果我们的数据稀疏，数据的特征有不同的特点，则我们可能不想对所有data更新到相同的程度，而是对很少发生的特征执行较大的更新
- 最小化神经网络常见的高度非凸误差函数的另一个关键挑战是避免陷入其众多次优局部最小值中，有人指出困难实际上不是由局部最小值产生的，而是由鞍点引起的，即一维向上倾斜而另一维向下倾斜的点，这些鞍点通常被相同误差的平稳段包围，这使SGD很难逃脱，因为在所有维度上梯度都接近于零
- 在鞍点附近，基于梯度的优化算法（几乎目前所有的实际使用的优化算法都是基于梯度的）会遇到较为严重的问题，鞍点处的梯度为零，鞍点通常被相同误差值的平面所包围（这个平面又叫Plateaus，Plateaus是梯度接近于零的平缓区域，会降低神经网络学习速度），在高维的情形，这个鞍点附近的平坦区域范围可能非常大，这使得SGD算法很难脱离区域，即可能会长时间卡在该点附近（因为梯度在所有维度上接近于零）。
- 鞍点和局部极小值相同的是，在该点处的梯度都等于零，不同在于在鞍点附近Hessian矩阵是不定的(行列式小于0)，而在局部极值附近的Hessian矩阵是正定的
Gradient descent optimization algorithms
Momentum
v t = γ v t − 1 + η ∇ θ J ( θ ) θ = θ − v t \begin{aligned} v_{t} &=\gamma v_{t-1}+\eta \nabla_{\theta} J(\theta) \\ \theta &=\theta-v_{t} \end{aligned} vtθ=γvt−1+η∇θJ(θ)=θ−vt
- 动量是一种有助于在相关方向上加速SGD并抑制振荡的方法主要是解决challenge one收敛波动。通过将过去时间步长的更新向量的分数γ与当前更新向量相加来完成此操作
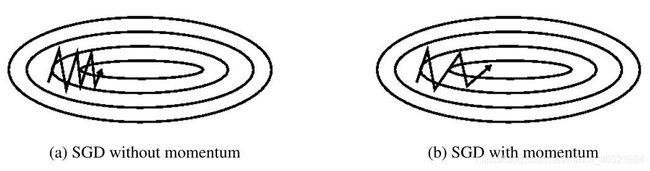
- 在峡谷地区（某些方向较另一些方向上陡峭的多，常见于局部极值点），SG方向会在这些地方附近震荡，从而导致收敛速度变慢，加动量项法就可解决这个问题。在更新模型参数时，对于那些当前梯度方向与上一次梯度方向相同的参数，应进行加强，即在这些方向上更快了，否则进行削减，通过使用Momentum我们可以获得更快的收敛速度并减少振荡。
- 使用动量时，类似于我们将球推下山坡。球在下坡时会积聚动量，在途中速度越来越快。
Nesterov accelerated gradient
v t = γ v t − 1 + η ∇ θ J ( θ − γ v t − 1 ) θ = θ − v t \begin{aligned} v_{t} &=\gamma v_{t-1}+\eta \nabla_{\theta} J\left(\theta-\gamma v_{t-1}\right) \\ \theta &=\theta-v_{t} \end{aligned} vtθ=γvt−1+η∇θJ(θ−γvt−1)=θ−vt
- 然而滚下山坡的这个球，希望不是盲目跟随山坡，而是更聪明一些，让这个球有个意识，知道在山坡再次变缓之前会减速
- 用 θ − γ v t − 1 \theta-\gamma v_{t-1} θ−γvt−1来近似当做参数下一步会变成的值，则在计算梯度时，不是在当前位置，而是它这个预测未来的位置上
- 特点
- 此预期更新可防止我们过快地执行并导致响应速度增加，从而显着提高了RNN在许多任务上的性能
- 此预期更新可防止我们过快地执行并导致响应速度增加，从而显着提高了RNN在许多任务上的性能
- 对比分析
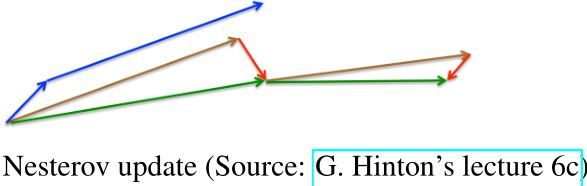
- 蓝色是 Momentum的过程，会先计算当前的梯度，然后在更新后的累积梯度后会有一个大的跳跃。
- 而 NAG 会先在前一步的累积梯度上(brown vector)有一个大的跳跃，然后衡量一下梯度做一下修正(red vector)，这种预期的更新可以避免我们走的太快
AdaGrad
E [ g 2 ] t = 0.9 E [ g 2 ] t − 1 + 0.1 g t 2 θ t + 1 = θ t − η E [ g 2 ] t + ϵ g t \begin{aligned} E\left[g^{2}\right]_{t} &=0.9 E\left[g^{2}\right]_{t-1}+0.1 g_{t}^{2} \\ \theta_{t+1} &=\theta_{t}-\frac{\eta}{\sqrt{E\left[g^{2}\right]_{t}+\epsilon}} g_{t} \end{aligned} E[g2]tθt+1=0.9E[g2]t−1+0.1gt2=θt−E[g2]t+ϵηgt
对上述 g t g_{t} gt学习率前系数还有下面这个公式的描述：
η s + ϵ \frac{\eta}{\sqrt{s+\epsilon}} s+ϵη
-
AdaGrad 算法做出的改进用来解决第二个挑战，对于学习率参数的选择，这个方法记录了每个参数的历史梯度平方和（平方是 element-wise的），并以此表征每个参数变化的剧烈程度，继而自适应地为变化剧烈的参数选择更小的学习率。
-
然而，我们希望学习率怎样变化呢？如果一个参数的梯度一直都非常大，就让它的学习率变小一点，防止震动，反之，则让其学习率变大，使其能更快更新，对每个参数，（初始化一个变量s=0，每次参数更新时，将梯度平方求和累加到s上）参数每次更新时将梯度平方和加到G上面（所以梯度越大，累加得s越大，学习率越小）所以梯度越大，累加得G越大，学习率越小
-
G 是一个对角阵，每个对角元素i，是t时间步长关于 θ i θ_{i} θi的梯度的平方和， ϵ \epsilon ϵ 是一个光滑项 (usuallyon the order of 1e−8)
-
特点
- 优点：学习率可以自适应的减小。在稀疏的样本下，下降的方向，涉及的变量可能有很大的差异。非常适用。
- 缺点：学习率过早、过量的减少。初始学习率需要手动设置 η \eta η。设置太大优化不稳定，设置太小，没到局部最有结果就停止了到后期，分母越来越大，学习率会变得较小，无法较好的收敛
RMSProp
E [ g 2 ] t = 0.9 E [ g 2 ] t − 1 + 0.1 g t 2 θ t + 1 = θ t − η E [ g 2 ] t + ϵ g t \begin{aligned} E\left[g^{2}\right]_{t} &=0.9 E\left[g^{2}\right]_{t-1}+0.1 g_{t}^{2} \\ \theta_{t+1} &=\theta_{t}-\frac{\eta}{\sqrt{E\left[g^{2}\right]_{t}+\epsilon}} g_{t} \end{aligned} E[g2]tθt+1=0.9E[g2]t−1+0.1gt2=θt−E[g2]t+ϵηgt
-
RMSProp通过使用递归递减的形式来记录历史梯度的平方和来解决Adagrad的缺陷。
-
简单来讲，给了历史累加的s一个权重，使其到后面不至于过大
-
起到的效果是在参数空间更为平缓的方向，会取得更大的进步（因为平缓，所以历史梯度平方和较小，对应学习下降的幅度较小），并且能够使得陡峭的方向变得平缓，从而加快训练速度。
-
特点：
- 解决了AdaGrad越到后面学习率会变得较小，无法较好的收敛
- 在参数空间更为平缓的方向，会取得更大的进步（因为平缓，所以历史梯度平方和较小，对应学习下降的幅度较小），并且能够使得陡峭的方向变得平缓，从而加快训练速度
- 鉴于神经网络都是非凸条件下的，RMSProp在非凸条件下结果更好，改变梯度累积为指数衰减的移动平均以丢弃遥远的过去历史
蓝色线是Adagrad算法，b方向上的梯度g要大于在w方向上的梯度，
绿色是RMSprop算法，梯度越大的反而更新越小，越小的值反而更新越大，那么后面的更新则会像下面绿色线更新一样，明显就会好于蓝色更新曲线
-
应用：对于RNN（循环网络效果比较好），处理序列问题，比如文本分类，序列预测
Adadelta
E [ Δ θ 2 ] t = γ E [ Δ θ 2 ] t − 1 + ( 1 − γ ) Δ θ t 2 R M S [ Δ θ ] t = E [ Δ θ 2 ] t + ϵ θ t + 1 = θ t − R M S [ Δ θ ] t − 1 R M S [ g ] t g t \begin{aligned} E\left[\Delta \theta^{2}\right]_{t} &=\gamma E\left[\Delta\theta^{2}\right]_{t-1}+(1-\gamma) \Delta \theta_{t}^{2}\\ R M S[\Delta \theta]_{t}&=\sqrt{E\left[\Delta \theta^{2}\right]_{t}+\epsilon}\\ \theta_{t+1}&=\theta_{t}-\frac{R M S[\Delta \theta]_{t-1}}{R M S[g]_{t}} g_{t} \end{aligned} E[Δθ2]tRMS[Δθ]tθt+1=γE[Δθ2]t−1+(1−γ)Δθt2=E[Δθ2]t+ϵ=θt−RMS[g]tRMS[Δθ]t−1gt
- 这个算法是对 Adagrad 的改进，和 Adagrad 相比，
- 1.就是分母的 G 换成了过去的梯度平方的衰减平均值，这样就能解决了AdaGrad越到后面学习率会变得较小，无法较好的收敛。
- 梯度更新规则还将学习率 η 换成了 RMS[Δθ]可以看到类似NSG方法，不需要提前设定学习率了，将过去时间步长的更新向量的分数γ与当前更新向量相加(相当于对更新加了一个权重)来完成此操作可以减少震荡
- 特点：
- 解决了Adagrad的学习率锐减的问题
- 不用提前设置学习率
- RMSprop 与 Adadelta的第一种形式相同：使用的是指数加权平均，旨在消除梯度下降中的摆动，与Momentum的效果一样，某一维度的导数比较大，则指数加权平均就大，某一维度的导数比较小，则其指数加权平均就小，这样就保证了各维度导数都在一个量级，进而减少了摆动。允许使用一个更大的学习率η
Adam
简单来讲 Adam 算法就是综合了 AdaGra 和 RMSProp 的一种算法，其既记录了历史梯度均值作为动量，又考虑了历史梯度平方和实现各个参数的学习率自适应调整，解决了 SGD 的上述两个问题。
结合AdaGrad和RMSProp两种优化算法的优点。对梯度的一阶矩估计（First Moment Estimation，即梯度的均值）和二阶矩估计进行综合考虑，计算出更新步长
可以看做修正后的Momentum+RMSProp算法
Adam对超参数的选择相当鲁棒，这里鲁棒就是不敏感，这样对于我们选择超参数就比较宽松一些
- 特点
- 结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点
- 实现简单，计算高效，对内存需求少
- 参数的更新不受梯度的伸缩变换影响
- 超参数具有很好的解释性，且通常无需调整或仅需很少的微调
- 更新的步长能够被限制在大致的范围内（初始学习率）
- 能自然地实现步长退火过程（自动调整学习率）
- 很适合应用于大规模的数据及参数的场景
- 适用于不稳定目标函数
- 适用于梯度稀疏或梯度存在很大噪声的问题
- 综合Adam在很多情况下算作默认工作性能比较优秀的优化器
- 缺点：虽然Adam算法目前成为主流的优化算法，不过在很多领域里（如计算机视觉的对象识别、NLP中的机器翻译）的最佳成果仍然是使用带动量（Momentum）的SGD来获取到的。Wilson 等人的论文结果显示，在对象识别、字符级别建模、语法成分分析等方面，自适应学习率方法（包括AdaGrad、AdaDelta、RMSProp、Adam等）通常比Momentum算法效果更差。
Nadam and Adammax
- Nadam类似于带有Nesterov动量项的Adam
- Adamax是Adam的一种变体，此方法对学习率的上限提供了一个更简单的范围
- 特点：
- Adamax学习率的边界范围更简单
- 一般而言，在想使用带动量的RMSprop，或者Adam的地方，大多可以使用Nadam取得更好的效果
对比图
-
鞍点对比图
-
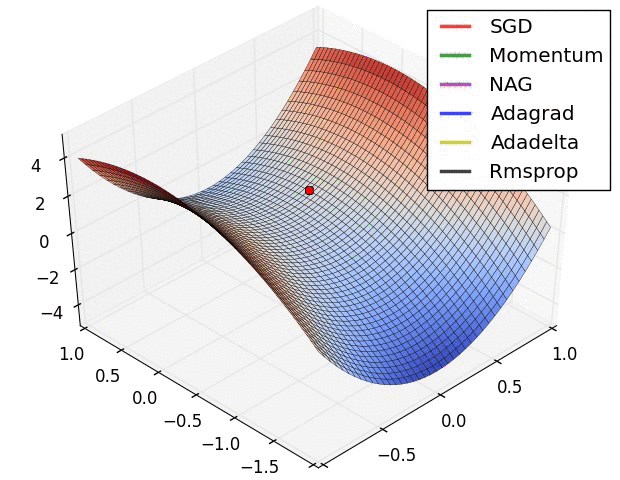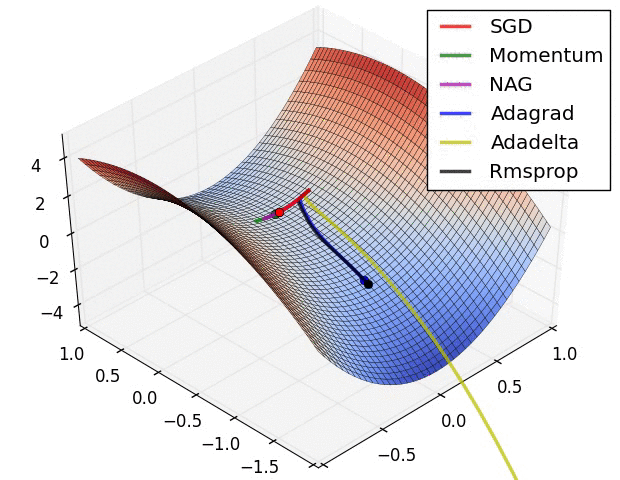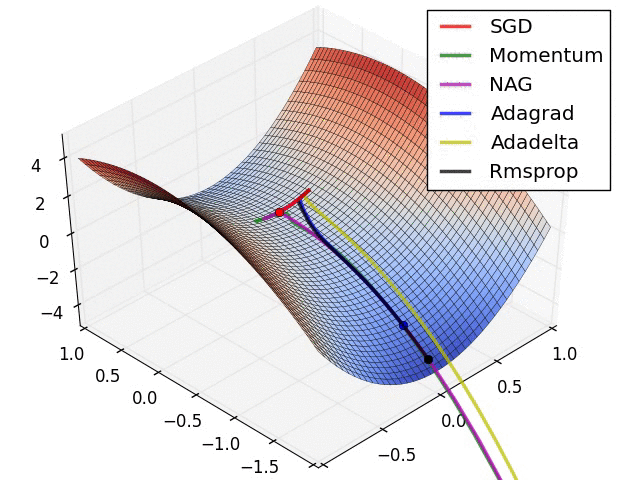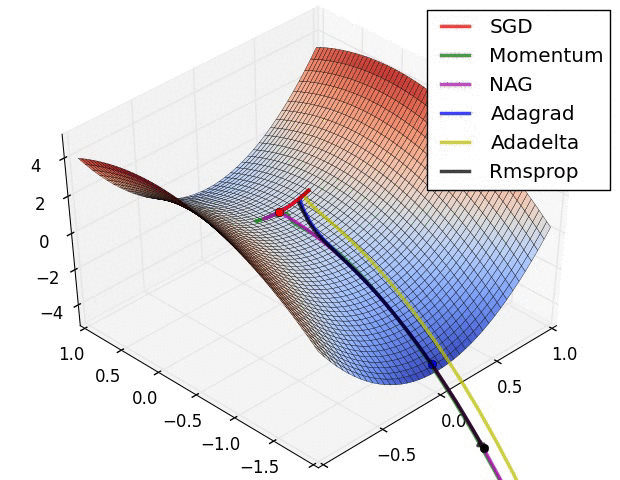
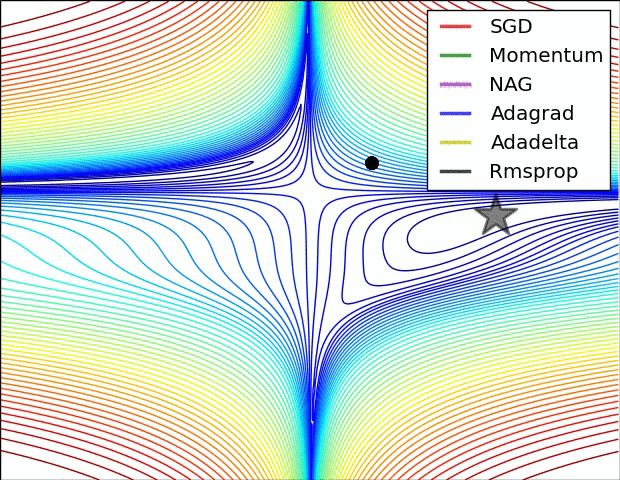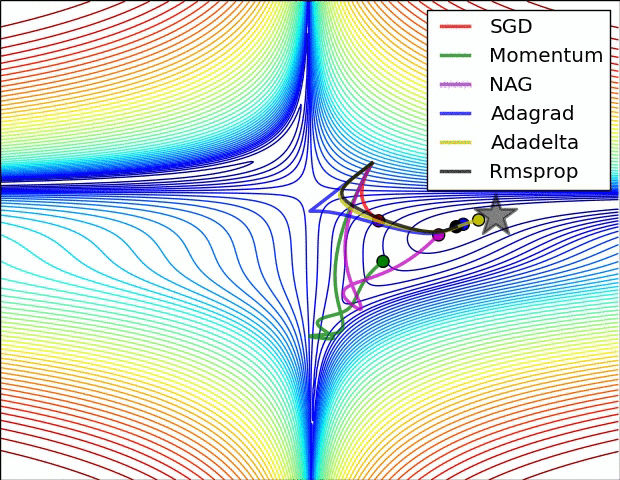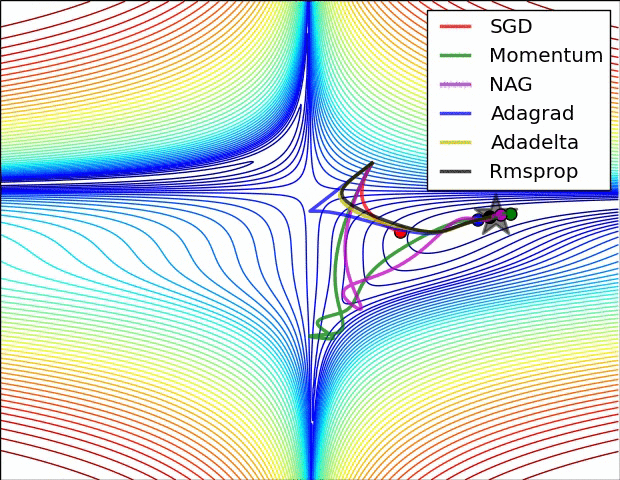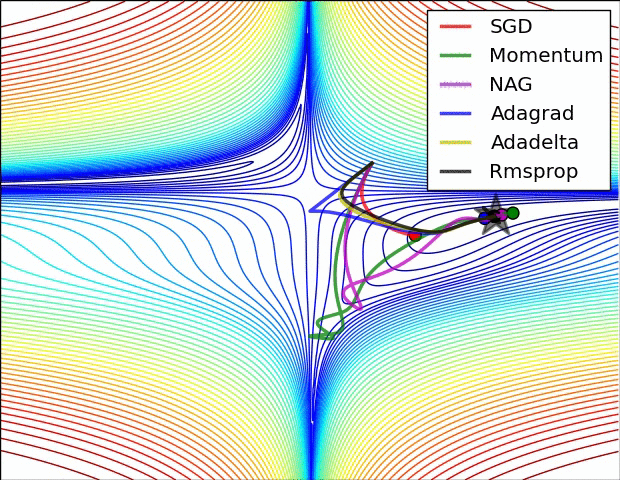
注意，Adagrad，Adadelta和RMSprop立即向正确的方向驶去，并以类似的速度收敛，而Momentum和NAG则偏离了赛道，让人联想起滚下山顶的球的形象。但是，由于NAG向前看并走到最低限度，因此响应能力增强，因此能够更快地纠正航向
-
损失等高线图
-
算法在鞍点处的行为方式，即一个维度的正斜率，而另一维度的负斜率，这对SGD造成了困难。请注意，SGD，Momentum和NAG很难打破对称性，尽管后两者最终设法摆脱了鞍点，而Adagrad，RMSprop和Adadelta则迅速下降到负斜率，而Adadelta领先
总结
- 对于稀疏数据，尽量使用学习率可自适应的优化方法，如果在意更快的收敛，并且需要训练较深较复杂的网络时，推荐使用学习率自适应的优化方法
- SGD通常训练时间更长，但是在好的初始化和学习率调度方案的情况下，结果更可靠
- Adadelta，RMSprop，Adam是比较相近的算法，在相似的情况下表现差不多，
- 在想使用带动量的RMSprop，或者Adam的地方，大多可以使用Nadam取得更好的效果
Which optimizer to use
- 如果输入数据稀疏，则可能会使用一种自适应学习率方法来获得最佳结果。另一个好处是您无需调整学习率，但可能会使用默认值获得最佳结果
- 总而言之，RMSprop是Adagrad的扩展，用于处理其学习率急剧下降的问题。它与Adadelta相同，除了Adadelta在分子更新规则中使用参数更新的RMS。最后，RMSprop添加了偏差校正和动量。就此而言，RMSprop，Adadelta和Adam是非常相似的算法，在相似的情况下效果很好。金马等。 [10]表明，随着梯度变得稀疏，它的偏差校正有助于Adam在优化结束时略胜于RMSprop。就目前而言，adam可能是最佳的整体选择
- 有趣的是，最近的许多论文都使用了没有动力的简单SGD和简单的学习速率退火时间表。如图所示，SGD通常可以找到最小值，但是与某些优化策略相比，它可能花费更长的时间，它更多地依赖于可靠的初始化和退火策略，并且可能卡在鞍点而不是局部最小值。因此，如果您关心快速收敛并训练一个深度或复杂的神经网络，则应该选择一种自适应学习率方法
Parallelizing and distributing SGD
- 考虑到大规模数据解决方案的普遍存在和低商品集群的可用性，分配SGD进一步加快速度是一个显而易见的选择。 SGD本身具有固有的顺序性：逐步，我们将进一步迈向最低限度。运行它可提供良好的收敛性，但可能会很慢，尤其是在大型数据集上。相反，异步运行SGD更快，但是工作人员之间的通信欠佳会导致收敛不佳。此外，我们还可以在一台机器上并行化SGD，而无需大型计算集群。以下是已提出的优化并行和分布式SGD的算法和体系结构。
Hogwild
介绍了一种称为Hogwild的更新方案！允许在CPU上并行执行SGD更新。允许处理器访问共享内存而无需锁定参数。这仅在输入数据稀疏的情况下有效，因为每次更新只会修改所有参数的一部分。他们表明，在这种情况下，更新方案几乎可以达到最佳的收敛速度，因为处理器不太可能会覆盖有用的信息。
Downpour SGD
- Downpour SGD是Dean等人使用的SGD的异步变体。 [6]在Google的DistBelief框架（TensorFlow的前身）中进行。它在训练数据的子集上并行运行模型的多个副本。这些模型将其更新发送到参数服务器，该参数服务器分布在许多计算机上。每台机器都负责存储和更新部分模型参数。但是，由于副本之间无法相互通信，例如通过共享权重或更新，它们的参数不断处于分散的风险中，从而阻碍收敛
Delay-tolerant Algorithms for SGD
- McMahan和Streeter [12]通过开发耐延迟算法将AdaGrad扩展到并行设置，该算法不仅适应过去的梯度，还适应更新延迟。实践证明，这很有效
- H. Brendan Mcmahan and Matthew Streeter. Delay-Tolerant Algorithms for Asynchronous
Distributed Online Learning. Advances in Neural Information Processing Systems (Proceedings
of NIPS), pages 1–9, 2014.
TensorFlow
- TensorFlow14 [1]是Google最近开源的框架，用于实施和部署大规模机器学习模型。它基于他们在DistBelief的经验，已经在内部用于在各种移动设备以及大规模分布式系统上执行计算。分布式版本（于201615年4月发布）依赖于一个计算图，该计算图被划分为每个设备的子图，而通信使用发送/接收节点对进行
Elastic A veraging SGD
- 张等 提出了Elastic A veraging SGD，其将异步SGD的工人的参数与弹性力（即由参数服务器存储的中心变量）联系起来。这允许局部变量与中心变量进一步波动，这在理论上允许对参数空间进行更多探索。他们凭经验表明，这种增加的勘探能力会通过发现新的局部最优来提高性能
Additional strategies for optimizing SGD
Shuffling and Curriculum Learning
- 通常，我们希望避免以有意义的顺序向我们的模型提供训练示例，因为这可能会使优化算法产生偏差。因此，通常最好在每个epoch之后对训练数据进行打乱shuffle
- 另一方面，在某些情况下，我们旨在解决日益棘手的问题，以有意义的顺序提供培训示例实际上可能会导致性能提高和更好的融合。建立这种有意义的顺序的方法称为课程学习（ Curriculum Learning）
- Zaremba和Sutskever只能训练LSTM来使用课程学习评估简单的程序，并且表明联合或混合策略比单纯的策略更好，后者通过增加难度来对示例进行排序
Batch normalization
- 为了促进学习，我们通常通过零均值和单位方差初始化参数的初始值来对其进行归一化。随着训练的进行以及我们将参数更新到不同的程度，我们将失去这种标准化，这会减慢训练速度，并随着网络的不断深入而放大变化
- 批处理规范化[9]为每个小型批处理重新建立这些规范化，并且更改也通过操作反向传播。通过将归一化作为模型体系结构的一部分，我们可以使用较高的学习率，而对初始化参数的关注较少。批处理规范化还可以充当正则化器，从而减少（有时甚至消除）对Dropout的需求。
Early stopping
-
应该在训练过程中始终监视验证集上的错误，如果验证错误没有得到足够的改善，请停止
-
Neelakantan et al. add noise that follows a Gaussian distribution N ( 0 , σ t 2 ) N(0, σ_{t}^{2}) N(0,σt2)to each gradient update:
-
他们表明，添加这种噪声可使网络对不良的初始化更加健壮，并有助于训练特别深而复杂的网络。他们怀疑增加的噪声使模型有更多的机会逃脱并找到新的局部极小值，这对于更深层的模型而言更为常见。
-
文章参考
《An overview of gradient descent optimization
algorithms》
https://zhuanlan.zhihu.com/p/22252270
https://www.cnblogs.com/ljygoodgoodstudydaydayup/p/7294671.html
https://blog.csdn.net/u012759136/article/details/52302426/