基于matlab编程二维空间内目标作匀速直线运动和匀速圆周运动的特点源码

T=2;
alpha=0.8;            %  加权衰减因子
window=1/(1-alpha);   %  检测机动的有效窗口长度
dt=100;               %  dt=dt_x=dt_y=100
Th=25;              %  机动检测门限
Ta=9.49;              %  退出机动的检测门限
N=800/T;              %　采样次数
M=50;                 %　模拟次数

%　真实轨迹数据
t=2:2:400;
    xo0=2000+0*t;
    yo0=10000-15*t;
t=402:2:600;
    xo1=2000+0.075*((t-400).^2)/2;
    yo1=10000-15*400-(15*(t-400)-0.075*((t-400).^2)/2);
t=602:2:610   ;
    xo2=xo1(100)+15*(t-600);
    yo2=yo1(100)+0*t;   
t=612:2:660;
    xo3=xo2(5)+(15*(t-610)-0.3*((t-610).^2)/2);
    yo3=yo2(5)-0.3*((t-610).^2)/2;
t=662:2:800;
    xo4=xo3(25)+0*t;
    yo4=yo3(25)-15*(t-660);
x=[xo0,xo1,xo2,xo3,xo4];
y=[yo0,yo1,yo2,yo3,yo4];

e_x1=zeros(1,N);
e_x2=zeros(1,N);
e_y1=zeros(1,N);
e_y2=zeros(1,N);
px=zeros(1,N);
qy=zeros(1,N);
u=zeros(1,N);
u_a=zeros(1,N);

for j=1:M
  no1=100*randn(1,N);       %  随机白噪
  no2=100*randn(1,N);
  for i=1:N;
    zx(i)=x(i)+no1(i);      %  观测数据
    zy(i)=y(i)+no2(i);
    z(:,i)=[zx(i);zy(i)];
  end  
  
%
X_estimate(2,:)=[zx(2),(zx(2)-zx(1))/T,zy(2),(zy(2)-zy(1))/T];
X_est=X_estimate(2,:);
P_estimate=[dt^2,dt^2/T,0,0;dt^2/T,(dt^2)*2/(T^2),0,0;0,0,dt^2,dt^2/T;0,0,dt^2/T,(dt^2)*2/(T^2)];
x1(1)=zx(1); y1(1)=zy(1); x1(2)=X_estimate(2,1); y1(2)=X_estimate(2,3);
u(1)=0; u(2)=0; 
u1=u(2);

pp=0;% ０表示非机动，１表示机动
qq=0;
rr=1;
k=3;
while k<=N    
    if k<=20
        z1=z(:,k);
        [X_pre,X_est,P_estimate,u1]=kalmanstatic(X_est,P_estimate,z1,k,u1);
        X_estimate(k,:)=X_est;
        X_predict(k,:)=X_pre;
        P(k,:)=[P_estimate(1,1),P_estimate(1,2),P_estimate(2,2),P_estimate(3,3),P_estimate(3,4),P_estimate(4,4)];
        x1(k)=X_estimate(k,1);
        y1(k)=X_estimate(k,3);
        u(k)=u1;
        k=k+1;
    else
        if pp==0  %　进入非机动模型
            if rr==window+1 %　由机动进入非机动模型，为防止回朔，至少递推window＋1次
                u1=0;
            else 
            end
            while rr>0
            z1=z(:,k);
            [X_pre,X_est,P_estimate,u1]=kalmanstatic(X_est,P_estimate,z1,k,u1);
            X_estimate(k,:)=X_est;
            X_predict(k,:)=X_pre;
            P(k,:)=[P_estimate(1,1),P_estimate(1,2),P_estimate(2,2),P_estimate(3,3),P_estimate(3,4),P_estimate(4,4)];
            x1(k)=X_estimate(k,1);
            y1(k)=X_estimate(k,3);
            u(k)=u1;
            rr=rr-1;
            end
            rr=1;
            if u(k)>=Th
                pp=1;qq=1; %　“pp=1，qq=1”表示由非机动进入机动模型
            else
            end
            k=k+1;
        else   %　机动模型
            if qq==1   %由非机动进入机动模型，需要进行修正
                k=k-window-1;  
                Xm_est=[X_estimate(k-1,:),0,0];
                Xm_pre=[X_predict(k,:),0,0];
                Pm_estimate=zeros(6,6);
                P=P(k-1,:);
                m=0;
            else      %在机动模型中进行递推
                Xm_est=Xm_estimate(k-1,:);  
            end
                z1=z(:,k);
                [Xm_est,Pm_estimate,ua1,qq,m]=kalmandynamic(Xm_pre,Xm_est,Pm_estimate,z1,k,P,qq,m);
                Xm_estimate(k,:)=Xm_est;
                x1(k)=Xm_estimate(k,1);
                y1(k)=Xm_estimate(k,3);
                ua(k)=ua1;
            if ua1                 X_est=Xm_estimate(k,1:4);
                P_estimate=Pm_estimate(1:4,1:4);
                pp=0; 
                rr=window+1;
            else
            end
            k=k+1;
        end
    end
end

for j=1:N
      px(1,j)=x1(1,j)+px(1,j);  %　迭加每次估计的数据
      qy(1,j)=y1(1,j)+qy(1,j);
 
      e_x1(j)=(x1(j)-x(j))+e_x1(j);
      e_y1(j)=(y1(j)-y(j))+e_y1(j);
      e_x2(j)=((x1(j)-x(j))^2)+e_x2(j);
      e_y2(j)=((y1(j)-y(j))^2)+e_y2(j);
end
end
for k=1:N
    px(1,k)=px(1,k)/M;
    qy(1,k)=qy(1,k)/M;
    e_x(k)=e_x1(k)/M;
    ex(k)=sqrt(e_x2(k)/M-e_x(k)^2);
    e_y(k)=e_y1(k)/M;
    ey(k)=sqrt(e_y2(k)/M-e_y(k)^2);
end
figure(1);
plot(x,y);axis([1500 5000 -2000 12000]);
figure(2);
plot(x,y,'b-',zx,zy,'k:',px,qy,'r');
legend('真实轨迹','观测轨迹','50次滤波轨迹');
figure(3);
plot(x,y,'k',x1,y1,'r');
legend('真实轨迹','一次滤波轨迹');

figure(4);
subplot(2,2,1),plot(e_x); title('X坐标 滤波误差均值曲线');
subplot(2,2,2),plot(e_y); title('Y坐标 滤波误差均值曲线');
subplot(2,2,3),plot(ex);  title('X坐标 滤波误差标准差曲线');
subplot(2,2,4),plot(ey);  title('Y坐标 滤波误差标准差曲线');
 

 

 

%%%%函数1静态模型
function[X_pre,X_est,P_estimate,u1]=kalmanstatic(X_est,P_estimate,z1,k,u1)
   T=2;
   alpha=0.8;            %  加权衰减因子
   Phi=[1,T,0,0;0,1,0,0;0,0,1,T;0,0,0,1];
   H=[1,0,0,0;0,0,1,0];
   I=[1,0,0,0;0,1,0,0;0,0,1,0;0,0,0,1];
   R=[10000,0;0,10000];  %  观测噪声方差阵
   X_estimate(k-1,:)=X_est;
    u(k-1)=u1;
    X_predict(k,:)=(Phi*X_estimate(k-1,:)')';
    P_predict=Phi*P_estimate*(Phi)';
    K=P_predict*(H)'*inv(H*P_predict*(H)'+R);
    X_estimate(k,:)=(X_predict(k,:)'+K*(z1-H*X_predict(k,:)'))';
    P_estimate=(I-K*H)*P_predict;
    X_est=X_estimate(k,:);
    X_pre=X_predict(k,:);

    v(:,k)=z1-H*(X_predict(k,:))';     %  新信息
    S=H*P_predict*H'+R;                %  新信息的方差阵
    delta(k)=v(:,k)'*inv(S)*v(:,k); 
    u(k)=alpha*u(k-1)+delta(k);
    u1=u(k);
 

 

%%函数2 动态模型
function [Xm_est,Pm_estimate,ua1,qq,m]=kalmandynamic(Xm_pre,Xm_est,Pm_estimate,z1,k,P,qq,m);
T=2;
I=diag([1,1,1,1,1,1]);
Phi=[1,T,0,0,(T^2)/2,0;0,1,0,0,T,0;0,0,1,T,0,(T^2)/2;0,0,0,1,0,T;0,0,0,0,1,0;0,0,0,0,0,1];
H=[1,0,0,0,0,0;0,0,1,0,0,0];
G=[(T^2)/2,0;T,0;0,(T^2)/2;0,T;1,0;0,1];
R=[10000,0;0,10000];     %  观测噪声方差阵
alpha=0.8;               %  加权衰减因子
window=1/(1-alpha);      %  检测机动的有效窗口长度
Xm_estimate(k-1,:)=Xm_est;
if qq==1   %由非机动进入机动模型，需进行修正， 初始化
    Xm_predict(k,:)=Xm_pre;
    Xm_estimate(k,5)=[z1(1)-Xm_predict(k,1)]*2/(T^2);
    Xm_estimate(k,6)=[z1(2)-Xm_predict(k,3)]*2/(T^2);
    Xm_estimate(k,1)=z1(1);
    Xm_estimate(k,3)=z1(2);
    Xm_estimate(k,2)=Xm_estimate(k-1,2)+Xm_estimate(k,5)*T;
    Xm_estimate(k,4)=Xm_estimate(k-1,4)+Xm_estimate(k,6)*T;
    % 修正协方差阵
    Pm_estimate(1,1)=R(1,1);
    Pm_estimate(3,3)=R(2,2);

    Pm_estimate(1,2)=R(1,1)*2/T;
    Pm_estimate(2,1)=Pm_estimate(1,2);
    Pm_estimate(3,4)=R(2,2)*2/T;
    Pm_estimate(4,3)=Pm_estimate(3,4);

    Pm_estimate(1,5)=R(1,1)*2/(T^2);
    Pm_estimate(5,1)=Pm_estimate(1,5);
    Pm_estimate(3,6)=R(2,2)*2/(T^2);
    Pm_estimate(6,3)=Pm_estimate(3,6);

    Pm_estimate(5,5)=[R(1,1)+P(1)+P(2)*2*T+P(3)*T*T]*4/(T^4);
    Pm_estimate(6,6)=[R(2,2)+P(4)+P(5)*2*T+P(6)*T*T]*4/(T^4);

    Pm_estimate(2,2)=R(1,1)*4/(T^2)+P(1)*4/(T^2)+P(3)+P(2)*4/T;
    Pm_estimate(4,4)=R(2,2)*4/(T^2)+P(4)*4/(T^2)+P(6)+P(5)*4/T;

    Pm_estimate(2,5)=R(1,1)*4/(T^3)+P(1)*4/(T^3)+P(3)*2/T+P(2)*6/(T^2);
    Pm_estimate(5,2)=Pm_estimate(2,5);
    Pm_estimate(4,6)=R(2,2)*4/(T^3)+P(4)*4/(T^3)+P(6)*2/T+P(5)*6/(T^2);
    Pm_estimate(6,4)=Pm_estimate(4,6);
    Xm_est=Xm_estimate(k,:);

    qq=0;%修正后，标志qq复位（不再初始化），ua1设为１０，使不进入非机动模型
    ua1=10;
    m=0;
else 
    %  滤波方程
    Xm_predict(k,:)=(Phi*Xm_estimate(k-1,:)')';
    Q=[(Xm_estimate(k-1,5)/20)^2,0;0,(Xm_estimate(k-1,6)/20)^2];
    Pm_predict=Phi*Pm_estimate*(Phi)'+G*Q*G';
    K=Pm_predict*(H)'*inv(H*Pm_predict*(H)'+R);
    Xm_estimate(k,:)=(Xm_predict(k,:)'+K*(z1-H*Xm_predict(k,:)'))';
    Pm_estimate=(I-K*H)*Pm_predict;
    Xm_est=Xm_estimate(k,:);
    m=m+1;
    delta(k)=[Xm_estimate(k,5),Xm_estimate(k,6)]*[Pm_estimate(5,5),0;0,Pm_estimate(6,6)]*[Xm_estimate(k,5);Xm_estimate(k,6)];
    if m>=window
        ua(k)=delta(k)+delta(k-1)+delta(k-2)+delta(k-3)+delta(k-4);
        ua1=ua(k);
    else
        ua1=10;
    end
end

 

 

 

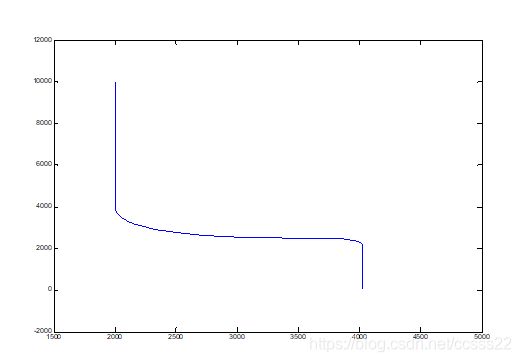
假定有一二座标雷达对一平面上运动的目标进行观测，目标在0-400秒沿着y轴作恒速直线运动，运动速度为-15米/秒，目标的起始点为(2000米,10000米)，在t= 400-600秒向轴x方向做的慢转弯，加速度为0.075米/秒，完成慢转弯后加速度将降为零，从t=610秒开始做90度的快转弯，加速度为0.3米/秒，在660秒结束转弯，加速度降至零。雷达扫描周期T=2秒，X和Y独立地进行观测，观测噪声的标准差均为100米。描述如下：

 

其中，程序算法中各参数为:

加权衰减因子, 机动检测门限; 退出机动的检测门限;

在跟踪的开始,首先采用非机动模型,从第20次采样开始,激活机动检测器。

 

 

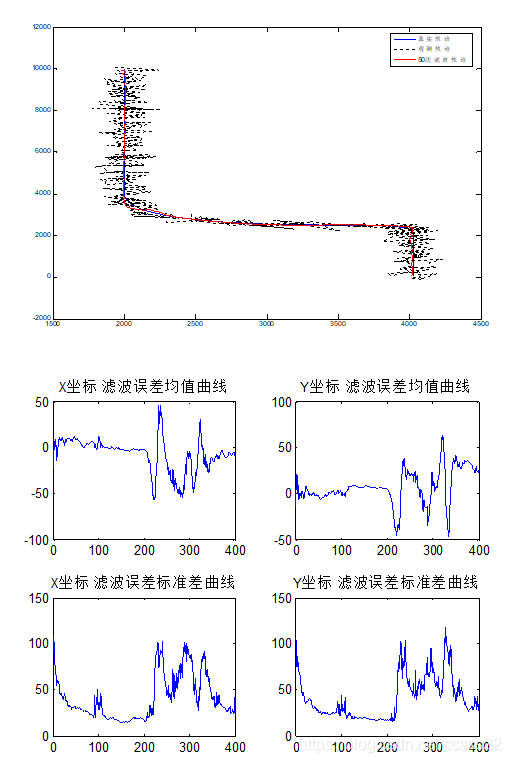
通过上图，可以看到：VD算法有4次机动,分别对应目标的2次加速运动,和2次匀速运动,符合目标真实轨迹变化。只是在模型出现机动的时候,会出现大的误差。在模型的调整过程中,可以明显发现:机动检测门限,退出机动的检测门限,加权衰减因子对算法的有效滤波有很大的影响，当目标快转弯时,会出现大的误差,这时候可以通过改变机动检测门限来减小。