NumPy构建多层感知机训练MNIST数据集
运行环境:python 3.6.12
1.加载MNIST数据集
1.1 代码
def load_data_wrapper():
# tr_d => {tuple:2}
# tr_d[0] => {ndarray:(50000, 784)}
# tr_d[1] => {ndarray:(50000,)}
tr_d, va_d, te_d = load_data()
# training_inputs => {list:50000}
# training_inputs[n] => {ndarray:(784, 1)}
training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]] # training_inputs对应神经网络最左边的784*1
# training_labels => {list:50000}
# training_labels[n] => {ndarray:(10, 1)}
training_labels = [vectorized_label(y) for y in tr_d[1]] # y对应实际手写数字值,training_labels对应神经网络最右边的10*1
# training_data => {list:50000}
# training_data[n] => {tuple:2}
# training_data[n][0] => {ndarray:(784, 1)}
# training_data[n][1] => {ndarray:(10, 1)}
training_data = list(zip(training_inputs, training_labels))
# validation_inputs => {list:10000}
# validation_inputs[n] => {ndarray:(784, 1)}
validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
# validation_data => {list:10000}
# validation_data[n] => {tuple:2}
# validation_data[n][0] => {ndarray:(784, 1)}
# validation_data[n][1] => {int64}
validation_data = list(zip(validation_inputs, va_d[1]))
# test_inputs => {list:10000}
# test_inputs[n] => {ndarray:(784, 1)}
test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
# test_data => {list:10000}
# test_data[n] => {tuple:2}
# test_data[n][0] => {ndarray:(784, 1)}
# test_data[n][1] => {int64}
test_data = list(zip(test_inputs, te_d[1]))
return training_data, validation_data, test_data
1.2 数据格式
2.one-hot处理标签特征
# 向量化标签,即对特征进行one-hot处理
def vectorized_label(j):
"""
:param j:一幅手写数字图对应的标签,dtype: int64
:return:
"""
e = np.zeros((10, 1))
e[j] = 1.0 # e[j][0] = 1.0也可以
return e
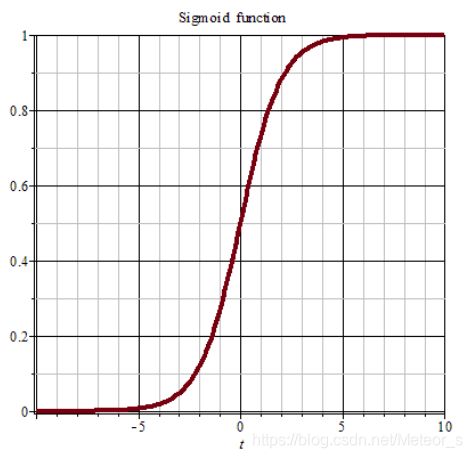
3.激活函数sigmoid
它可以将一个实数映射到(0,1)的区间,公式定义:
s i g m o i d ( x ) = 1 1 + e − x sigmoid(x)=\frac{1}{1+e^{-x}} sigmoid(x)=1+e−x1
def sigmoid(z): # 激活函数之前的值称之为z
return 1.0/(1.0+np.exp(-z))
其对x的导数:
s i g m o i d ′ ( x ) = e − x ( 1 + e − x ) 2 = s i g m o i d ( x ) ( 1 − s i g m o i d ( x ) ) sigmoid'(x)=\frac{e^{-x}}{(1+e^{-x})^2}=sigmoid(x)(1-sigmoid(x)) sigmoid′(x)=(1+e−x)2e−x=sigmoid(x)(1−sigmoid(x))
def dsigmoid(z): # sigmoid的导数
return sigmoid(z)(1-sigmoid(z))
4.实现 MLP_np 类
4.1 神经网络图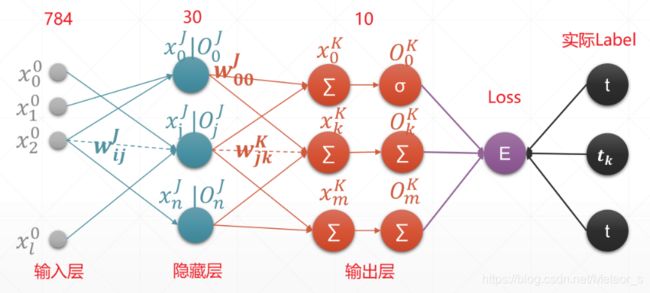
4.2 初始化函数
def __init__(self, sizes):
"""
:param sizes:[784, 30, 10]
"""
# sizes:[784, 30, 10]
# w:[ch_out, ch_in]
# b:[ch_out]
self.sizes = sizes
self.num_layers = len(sizes) - 1 # 网络层数2层
# weights => {list:2}
# weights[0] => {ndarray:(30, 784)}
# weights[1] => {ndarray:(10, 30)}
self.weights = [np.random.randn(ch2, ch1) for ch1, ch2 in zip(sizes[:-1], sizes[1:])] # [784, 30], [30, 10]
# biases => {list:2}
# biases[0] => {ndarray:(30, 1)}
# biases[1] => {ndarray:(10, 1)}
self.biases = [np.random.randn(ch, 1) for ch in sizes[1:]] # z = wx + b 因为wx是[30, 1],所以b也是[30, 1]
4.3 反向传播
def backprop(self, x, y):
"""
:param x: 图片数据{ndarray:(784, 1)}
:param y: 标签信息{ndarray:(10, 1)}
:return:
"""
# nabla_w => {list:2}
# nabla_w[0] => {ndarray:(30, 784)}
# nabla_w[1] => {ndarray:(10, 30)}
nabla_w = [np.zeros(w.shape) for w in self.weights] # 新建和self.weights同维度的列表,存储梯度信息
# nabla_b => {list:2}
# nabla_b[0] => {ndarray:(30, 1)}
# nabla_b[1] => {ndarray:(10, 1)}
nabla_b = [np.zeros(b.shape) for b in self.biases] # 新建和self.biases同维度的列表,存储梯度信息
# 1.前向传播
zs = [] # 保存每一层输出值
activations = [x] # 保存每一层激活值
activation = x # 保存输入数据
# 单独写forward是为了test的时候用,test不需要反向传播
for b, w in zip(self.biases, self.weights): # zip返回ndarray对象,b[0]w[0], b[1]w[1]
z = np.dot(w, activation) + b # z = wx + b,激活函数前的值称为z
activation = sigmoid(z) # z经过激活函数输出,作为下一层的输入
zs.append(z) # 记录z方便以后计算梯度
activations.append(activation) # 记录activation方便以后计算梯度
loss = np.power(activations[-1] - y, 2).sum() # 计算loss,不加sum的话返回向量
# 2.反向传播
# 2.1 计算输出层梯度
delta = activations[-1] * (1-activations[-1]) * (activations[-1] - y) # 点乘 [10, 1] with [10, 1] => [10, 1]
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].T) # 矩阵[10,1]@[1,30]才会得到[10,30],而activations[-2]维度为[30,1],所以activations[-2]需要加一个转置
# 2.2 计算隐藏层梯度
z = zs[-2]
a = activations[-2]
# [10, 30]T @ [10, 1] => [30, 10] @ [10, 1] => [30,1] 因为公式有求和在,所以是矩阵相乘
# [30, 1] * [30, 1] => [30, 1]
delta = np.dot(self.weights[-1].T, delta) * a * (1 - a)
nabla_b[-2] = delta
# [30, 1] @ [784, 1]T => [30, 784]
nabla_w[-2] = np.dot(delta, activations[-3].T) # 本质上是对应位置相乘,但是因为数据存储格式不一样,所以采用了矩阵相乘的方式
return nabla_w, nabla_b, loss
Loss函数:
M S E = 1 M ∑ m = 1 M x y ( y m − y ^ m ) 2 MSE =\frac{1}{M}\displaystyle \sum^{M}_{m=1}{\frac{x}{y}} (y_m-\hat y_m)^2 MSE=M1m=1∑Myx(ym−y^m)2
输出层计算梯度: k ∈ K k \in K k∈K
∂ E ∂ W j k = O j δ k \frac{\partial E}{\partial W_{jk}}=O_j\delta_k ∂Wjk∂E=Ojδk
∂ E ∂ b = δ k \frac{\partial E}{\partial b}=\delta_k ∂b∂E=δk
δ k = O k ( 1 − O k ) ( O k − t k ) \delta_k=O_k(1-O_k)(O_k-t_k) δk=Ok(1−Ok)(Ok−tk)
隐藏层计算梯度: j ∈ J j \in J j∈J
∂ E ∂ W i j = O i δ j \frac{\partial E}{\partial W_{ij}}=O_i\delta_j ∂Wij∂E=Oiδj
∂ E ∂ b = δ k \frac{\partial E}{\partial b}=\delta_k ∂b∂E=δk
δ j = O j ( 1 − O j ) ∑ k ∈ K δ k W j k \delta_j=O_j(1-O_j)\underset{k\in K}{\sum}\delta_kW_{jk} δj=Oj(1−Oj)k∈K∑δkWjk
4.4 训练
def train(self, training_data, epochs, batchsz, lr, test_data):
"""
:param training_data: [((784, 1),(10, 1))_0,...((784, 1),(10, 1))_49999] 训练数据50000条
:param epochs: 1000
:param batchsz: 10
:param lr: 0.01
:param test_data: [((784, 1),(10, 1))_0,...((784, 1),(10, 1))_9999] 测试数据10000条
:return:
"""
if test_data:
n_test = len(test_data) # 记录测试数据长度 10000
n = len(training_data) # 记录训练数据长度 50000
for j in range(epochs):
random.shuffle(training_data) # 打散训练数据
# 切割数据,切割成一个一个batch的,每个mini_batches包含10组训练数据
mini_batches = [training_data[k:k+batchsz] for k in range(0, n, batchsz)]
# mini_batch => {list:10}
# mini_batch[n] => {tuple:2}
# mini_batch[n][0] => {ndarray:(784, 1)}
# mini_batch[n][1] => {ndarray:(10, 1)}
for mini_batch in mini_batches:
loss = self.update_mini_batch(mini_batch, lr) # 在每个batch上更新weights和biases,返回loss
if test_data:
print("Epoch {0}: {1} / {2}".format(
j, self.evaluate(test_data), n_test), loss)
else:
print("Epoch {0} complete".format(j))
4.5 更新网络参数
def update_mini_batch(self, batch, lr):
"""
:param batch:[((784, 1),(10, 1))_0,...((784, 1),(10, 1))_9] 总共10条数据
:param lr:0.01
:return:
"""
nabla_w = [np.zeros(w.shape) for w in self.weights]
nabla_b = [np.zeros(b.shape) for b in self.biases]
loss = 0
# x:{ndarray:(784, 1)}
# y:{ndarray:(10, 1)}
for x, y in batch:
nabla_w_, nabla_b_, loss_ = self.backprop(x, y) # 返回更新后的梯度、偏置和loss
nabla_w = [accu+cur for accu, cur in zip(nabla_w, nabla_w_)] # 相应位置进行累加
nabla_b = [accu+cur for accu, cur in zip(nabla_b, nabla_b_)]
loss += loss_
nabla_w = [w/len(batch) for w in nabla_w] # 点除,取平均值
nabla_b = [b/len(batch) for b in nabla_b]
loss = loss / len(batch)
self.weights = [w - lr * nabla for w, nabla in zip(self.weights, nabla_w)] # w = w - lr * nabla_w 更新w
self.biases = [b - lr * nabla for b, nabla in zip(self.biases, nabla_b)] # b = b - lr * nabla_b 更新b
return loss
4.6 统计正确识别的个数
def evaluate(self, test_data):
"""
:param test_data:
:return:
"""
# result => {list:10000}
# result[n] => {tuple:2}
# result[n][0] => {int64}
# result[n][1] => {int64}
result = [(np.argmax(self.forward(x)), y) for x, y in test_data] # y不是one-hot编码,y是标量!
correct = sum(int(pred == y) for pred, y in result) # 返回识别对的个数
return correct
5.main函数
def main():
import mnist_loader
training_data, validation_data, test_data = mnist_loader.load_data_wrapper() # 加载MNIST数据集
net = MLP_np([784, 30, 10]) # 建立神经网络
net.train(training_data, epochs=1000, batchsz=10, lr=0.01, test_data=test_data) # 训练神经网络
6.完整代码
mnist_loader.py
"""
mnist_loader
~~~~~~~~~~~~
A library to load the MNIST image data. For details of the data
structures that are returned, see the doc strings for ``load_data``
and ``load_data_wrapper``. In practice, ``load_data_wrapper`` is the
function usually called by our neural network code.
"""
# Libraries
# Standard library
import pickle
import gzip
import numpy as np
def load_data():
f = gzip.open('mnist.pkl.gz', 'rb')
training_data, validation_data, test_data = pickle.load(f, encoding='bytes')
f.close()
return training_data, validation_data, test_data
def load_data_wrapper():
# tr_d => {tuple:2}
# tr_d[0] => {ndarray:(50000, 784)}
# tr_d[1] => {ndarray:(50000,)}
tr_d, va_d, te_d = load_data()
# training_inputs => {list:50000}
# training_inputs[n] => {ndarray:(784, 1)}
training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]] # training_inputs对应神经网络最左边的784*1
# training_labels => {list:50000}
# training_labels[n] => {ndarray:(10, 1)}
training_labels = [vectorized_label(y) for y in tr_d[1]] # y对应实际手写数字值,training_labels对应神经网络最右边的10*1
# training_data => {list:50000}
# training_data[n] => {tuple:2}
# training_data[n][0] => {ndarray:(784, 1)}
# training_data[n][1] => {ndarray:(10, 1)}
training_data = list(zip(training_inputs, training_labels))
# validation_inputs => {list:10000}
# validation_inputs[n] => {ndarray:(784, 1)}
validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
# validation_data => {list:10000}
# validation_data[n] => {tuple:2}
# validation_data[n][0] => {ndarray:(784, 1)}
# validation_data[n][1] => {int64}
validation_data = list(zip(validation_inputs, va_d[1]))
# test_inputs => {list:10000}
# test_inputs[n] => {ndarray:(784, 1)}
test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
# test_data => {list:10000}
# test_data[n] => {tuple:2}
# test_data[n][0] => {ndarray:(784, 1)}
# test_data[n][1] => {int64}
test_data = list(zip(test_inputs, te_d[1]))
return training_data, validation_data, test_data
# 向量化标签,即对特征进行one-hot处理
def vectorized_label(j):
"""
:param j:一幅手写数字图对应的标签,dtype: int64
:return:
"""
e = np.zeros((10, 1))
e[j] = 1.0 # e[j][0] = 1.0也可以
return e
mlp_np.py
import numpy as np
import random
def sigmoid(z): # 激活函数之前的值称之为z
return 1.0/(1.0+np.exp(-z))
def dsigmoid(z): # sigmoid的导数
return sigmoid(z)(1-sigmoid(z))
class MLP_np:
def __init__(self, sizes):
"""
:param sizes:[784, 30, 10]
"""
# sizes:[784, 30, 10]
# w:[ch_out, ch_in]
# b:[ch_out]
self.sizes = sizes
self.num_layers = len(sizes) - 1 # 网络层数2层
# weights => {list:2}
# weights[0] => {ndarray:(30, 784)}
# weights[1] => {ndarray:(10, 30)}
self.weights = [np.random.randn(ch2, ch1) for ch1, ch2 in zip(sizes[:-1], sizes[1:])] # [784, 30], [30, 10]
# biases => {list:2}
# biases[0] => {ndarray:(30, 1)}
# biases[1] => {ndarray:(10, 1)}
self.biases = [np.random.randn(ch, 1) for ch in sizes[1:]] # z = wx + b 因为wx是[30, 1],所以b也是[30, 1]
def forward(self, x):
"""
:param x: 输入的图片数据 {ndarray:(784, 1)}
:return: 前向传播生成的数据 {ndarray:(10, 1)}
"""
for b, w in zip(self.biases, self.weights):
# [30, 784] @ [784, 1] => [30, 1]
# [30, 1] + [30, 1] => [30, 1]
z = np.dot(w, x) + b # 矩阵相乘
# [30, 1]
x = sigmoid(z)
return x
def backprop(self, x, y):
"""
:param x: 图片数据{ndarray:(784, 1)}
:param y: 标签信息{ndarray:(10, 1)}
:return:
"""
# nabla_w => {list:2}
# nabla_w[0] => {ndarray:(30, 784)}
# nabla_w[1] => {ndarray:(10, 30)}
nabla_w = [np.zeros(w.shape) for w in self.weights] # 新建和self.weights同维度的列表,存储梯度信息
# nabla_b => {list:2}
# nabla_b[0] => {ndarray:(30, 1)}
# nabla_b[1] => {ndarray:(10, 1)}
nabla_b = [np.zeros(b.shape) for b in self.biases] # 新建和self.biases同维度的列表,存储梯度信息
# 1.前向传播
zs = [] # 保存每一层输出值
activations = [x] # 保存每一层激活值
activation = x # 保存输入数据
# 单独写forward是为了test的时候用,test不需要反向传播
for b, w in zip(self.biases, self.weights): # zip返回ndarray对象,b[0]w[0], b[1]w[1]
z = np.dot(w, activation) + b # z = wx + b,激活函数前的值称为z
activation = sigmoid(z) # z经过激活函数输出,作为下一层的输入
zs.append(z) # 记录z方便以后计算梯度
activations.append(activation) # 记录activation方便以后计算梯度
loss = np.power(activations[-1] - y, 2).sum() # 计算loss,不加sum的话返回向量
# 2.反向传播
# 2.1 计算输出层梯度
delta = activations[-1] * (1 - activations[-1]) * (activations[-1] - y) # 点乘 [10, 1] with [10, 1] => [10, 1]
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[
-2].T) # 矩阵[10,1]@[1,30]才会得到[10,30],而activations[-2]维度为[30,1],所以activations[-2]需要加一个转置
# 2.2 计算隐藏层梯度
z = zs[-2]
a = activations[-2]
# [10, 30]T @ [10, 1] => [30, 10] @ [10, 1] => [30,1] 因为公式有求和在,所以是矩阵相乘
# [30, 1] * [30, 1] => [30, 1]
delta = np.dot(self.weights[-1].T, delta) * a * (1 - a)
nabla_b[-2] = delta
# [30, 1] @ [784, 1]T => [30, 784]
nabla_w[-2] = np.dot(delta, activations[-3].T) # 本质上是对应位置相乘,但是因为数据存储格式不一样,所以采用了矩阵相乘的方式
return nabla_w, nabla_b, loss
def train(self, training_data, epochs, batchsz, lr, test_data):
"""
:param training_data: [((784, 1),(10, 1))_0,...((784, 1),(10, 1))_49999] 训练数据50000条
:param epochs: 1000
:param batchsz: 10
:param lr: 0.01
:param test_data: [((784, 1),(10, 1))_0,...((784, 1),(10, 1))_9999] 测试数据10000条
:return:
"""
if test_data:
n_test = len(test_data) # 记录测试数据长度 10000
n = len(training_data) # 记录训练数据长度 50000
for j in range(epochs):
random.shuffle(training_data) # 打散训练数据
# 切割数据,切割成一个一个batch的,每个mini_batches包含10组训练数据
mini_batches = [training_data[k:k + batchsz] for k in range(0, n, batchsz)]
# mini_batch => {list:10}
# mini_batch[n] => {tuple:2}
# mini_batch[n][0] => {ndarray:(784, 1)}
# mini_batch[n][1] => {ndarray:(10, 1)}
for mini_batch in mini_batches:
loss = self.update_mini_batch(mini_batch, lr) # 在每个batch上更新weights和biases,返回loss
if test_data:
print("Epoch {0}: {1} / {2}".format(
j, self.evaluate(test_data), n_test), loss)
else:
print("Epoch {0} complete".format(j))
def update_mini_batch(self, batch, lr):
"""
:param batch:[((784, 1),(10, 1))_0,...((784, 1),(10, 1))_9] 总共10条数据
:param lr:0.01
:return:
"""
nabla_w = [np.zeros(w.shape) for w in self.weights]
nabla_b = [np.zeros(b.shape) for b in self.biases]
loss = 0
# x:{ndarray:(784, 1)}
# y:{ndarray:(10, 1)}
for x, y in batch:
nabla_w_, nabla_b_, loss_ = self.backprop(x, y) # 返回更新后的梯度、偏置和loss
nabla_w = [accu + cur for accu, cur in zip(nabla_w, nabla_w_)] # 相应位置进行累加
nabla_b = [accu + cur for accu, cur in zip(nabla_b, nabla_b_)]
loss += loss_
nabla_w = [w / len(batch) for w in nabla_w] # 点除,取平均值
nabla_b = [b / len(batch) for b in nabla_b]
loss = loss / len(batch)
self.weights = [w - lr * nabla for w, nabla in zip(self.weights, nabla_w)] # w = w - lr * nabla_w 更新w
self.biases = [b - lr * nabla for b, nabla in zip(self.biases, nabla_b)] # b = b - lr * nabla_b 更新b
return loss
def evaluate(self, test_data):
"""
:param test_data:
:return:
"""
# result => {list:10000}
# result[n] => {tuple:2}
# result[n][0] => {int64}
# result[n][1] => {int64}
result = [(np.argmax(self.forward(x)), y) for x, y in test_data] # y不是one-hot编码,y是标量!
correct = sum(int(pred == y) for pred, y in result) # 返回识别对的个数
return correct
def main():
import mnist_loader
training_data, validation_data, test_data = mnist_loader.load_data_wrapper() # 加载MNIST数据集
net = MLP_np([784, 30, 10]) # 建立神经网络
net.train(training_data, epochs=1000, batchsz=10, lr=0.01, test_data=test_data) # 训练神经网络
if __name__ == '__main__':
main()