6、多层神经网络

前言：

经过之前的5个博客内容，我们已经完成了运用已有的数据集进行了一个简单的手写识别并且对参数进行了训练，使识别精确更加的准确。但是之前的神经网络只是用两层，一个输入层，一个输出层。但是一般的神经网络是有三层，输入层，隐藏层，输出层。我们现在就在原来的基础上再添加一层，隐藏层。当然隐藏层可以有很多层，我们这里实现一层之后，实现多层也是用一样的方法。那我们现在就开始吧！

步骤：

1、导入所需要的库

正所谓：工欲善其事，必先利其器。要想实现神经网络，就要先把所需要的工具都准备好。在这里就导入各种模块和拓展程序库了。

numpy： Numerical Python 是 Python 语言的一个扩展程序库，支持大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库。
math: math库是python提供的内置数学类函数库，math库不支持复数类型，仅支持整数和浮点数运算。
struct: struct 模块提供了用于在字节字符串和Python原生数据类型之间转换函数，比如数字和字符串。
pickle: 模块 pickle 实现了对一个Python 对象结构的二进制序列化和反序列化。
pathlib ： 该模块提供表示文件系统路径的类，其语义适用于不同的操作系统。
matplotlib.pyplot： matplotlib的pyplot子库提供了和matlab类似的绘图API，方便用户快速绘制2D图表。
tqdm: tqdm是一个快速，可扩展的Python进度条，可以在Python 长循环中添加一个进度提示信息，用户只需要封装任意的迭代器 tqdm(iterator)。
copy: Python自带名为copy的库，用于赋值，浅拷贝，深拷贝。

import numpy as np
import math,struct,pickle
from pathlib import Path
import matplotlib.pyplot as plt
from tqdm import tqdm
import copy

2、确定神经网络结构及参数

这次要完成有三个神经元的神经网络，就是在之前的基础上再加一层。参数也是用之前给出的结构来确定。第一层的输入层还是接收一个图片的数据，28×28。第二层隐藏层，就定一个100吧，这个隐藏层可以根据需求来定义。第三层输出层就还是10，表示0~9十个数。至于参数的确定，根据之前在博客中的内容可以确定为如下代码中的形式。

#三层神经元的数据维数
dimensions=[28*28,100,10]
#对应三层激活函数
activation=[bypass,tanh,softmax]
#每一层的参数
distribution=[
    {}, #第0层就是原样输出，不用参数
    {'b':[0,0],'w':[-math.sqrt(6/(dimensions[0]+dimensions[1])),math.sqrt(6/(dimensions[0]+dimensions[1]))]},
    {'b':[0,0],'w':[-math.sqrt(6/(dimensions[1]+dimensions[2])),math.sqrt(6/(dimensions[1]+dimensions[2]))]},
]

3、确定激活函数及其导数和验证

这里为了方便，我们把第一层接收的数据直接进行输出，就是第一次激活函数f(x)=x，则第一层激活函数的导数就是1；第二层的激活函数就是softmax；第三层的激活函数是tanh;再把三个激活函数放入字典当中，方便我们调用。这个时候我们要注意第二层激活函数的导数d_tanh，返回的是一个数而不是一个向量。所以因为到后面对参数求偏导时，有些部分要进行向量运算，而这就涉及到数乘和点积的问题了。所以这边再定义一个运算类型d_type，根据激活函数的不同来进行不同的运算。

#第一层激活函数
def bypass(x):
    return x
#第二层激活函数
def tanh(x):
    return np.tanh(x)
#第三层激活函数
def softmax(x):
    exp=np.exp(x-x.max())
    return exp/exp.sum()
#第一层激活函数导数
def d_bypass(x):
    return 1
#第二层激活函数导数  
def d_tanh(data):
    return 1/(np.cosh(data))**2
#第三层激活函数导数
def d_softmax(data):
    sm=softmax(data)
    return np.diag(sm)-np.outer(sm,sm)
#导数字典
differential={softmax:d_softmax,tanh:d_tanh,bypass:d_bypass}

d_type={bypass:'times',softmax:'dot',tanh:'times'}

激活函数导数验证如下：
softmax:

h=0.0001
func=softmax
input_len=4
for i in range(input_len):
    test_input=np.random.rand(input_len)
    derivative=differential[func](test_input)
    value1=func(test_input)
    test_input[i]+=h
    value2=func(test_input)
    print(derivative[i]-(value2-value1)/h)

结果：符合，在误差允许范围之内

tanh:

h=0.000001
func=tanh
input_len=4
for i in range(input_len):
    test_input=np.random.rand(input_len)
    derivative=differential[func](test_input)
    value1=func(test_input)
    test_input[i]+=h
    value2=func(test_input)
    print(derivative[i]-((value2-value1)/h)[i])

结果：符合，在误差允许范围之内

4、进行参数初始化

跟之前博客中的参数初始化一样的代码，不用对其进行修改，因为用的就是for循环来实现的。代码如下：

def init_parameters_b(layer):
    dist=distribution[layer]['b']
    return np.random.rand(dimensions[layer])*(dist[1]-dist[0])+dist[0]
def init_parameters_w(layer):
    dist=distribution[layer]['w']
    return np.random.rand(dimensions[layer-1],dimensions[layer])*(dist[1]-dist[0])+dist[0]
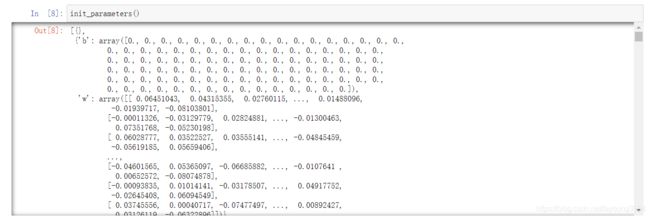
def init_parameters():
    parameter=[]
    for i in range(len(distribution)):
        layer_parameter={}
        for j in distribution[i].keys():
            if j=='b':
                layer_parameter['b']=init_parameters_b(i)
                continue
            if j=='w':
                layer_parameter['w']=init_parameters_w(i)
                continue
        parameter.append(layer_parameter)
    return parameter

初始化结果（一部分）如下：

5、导入数据集

现在有了参数，就缺导入的数据了。这里还是用MNIST数据集，对它进行导入。MNIST数据集里有三部分，训练集、验证集、测试集。这三个中的每一个里都有若干图片img和与之对应的标签label。
代码如下：

#MNIST数据集的地址
dataset_path=Path('../Scripts/MNIST')
train_img_path=dataset_path/'train-images.idx3-ubyte'
train_lab_path=dataset_path/'train-labels.idx1-ubyte'
test_img_path=dataset_path/'t10k-images.idx3-ubyte'
test_lab_path=dataset_path/'t10k-labels.idx1-ubyte'

train_num=50000#训练集的数量
valid_num=10000#验证集的数量
test_num=10000#测试集的数量

with open(train_img_path,'rb') as f:
    struct.unpack('>4i',f.read(16))
    tmp_img=np.fromfile(f,dtype=np.uint8).reshape(-1,28*28)/255
    train_img=tmp_img[:train_num]
    valid_img=tmp_img[train_num:]
    
with open(test_img_path,'rb') as f:
    struct.unpack('>4i',f.read(16))
    test_img=np.fromfile(f,dtype=np.uint8).reshape(-1,28*28)/255

with open(train_lab_path,'rb') as f:
    struct.unpack('>2i',f.read(8))
    tmp_lab=np.fromfile(f,dtype=np.uint8)
    train_lab=tmp_lab[:train_num]
    valid_lab=tmp_lab[train_num:]
    
with open(test_lab_path,'rb') as f:
    struct.unpack('>2i',f.read(8))
    test_lab=np.fromfile(f,dtype=np.uint8)

6、查看数据集

我们现在已经导入了数据集，那就要看看数据集里面有什么。

#查看训练集
def show_train(index):
    plt.imshow(train_img[index].reshape(28,28),cmap='gray')
    print('label : {}'.format(train_lab[index]))
#查看验证集
def show_valid(index):
    plt.imshow(valid_img[index].reshape(28,28),cmap='gray')
    print('label : {}'.format(valid_lab[index]))
#查看测试集
def show_test(index):
    plt.imshow(test_img[index].reshape(28,28),cmap='gray')
    print('label : {}'.format(test_lab[index]))

训练集中的随机一个图片

show_train(np.random.randint(train_num))

验证集中的随机一个图片

show_vaild(np.random.randint(vaild_num))

测试集中的随机一个图片

show_test(np.random.randint(test_num))

由此我们可以看到在训练集和验证集中，图片上的数字大部分是和标签是相对应的，也就是精确度较高。而在测试集中，碰到模棱两可的就有一些不太准确了。这是由三个小数据集的特性导致的。把我们写的神经网络想象成人的学习行为。我们的神经网络在训练集里要干的事情就是在上课，学习老师讲的知识点；在验证集里要干的事情是做作业，对老师讲的知识点进行巩固；在测试集里的要干的事情就是考试，运用已经掌握的知识点对没有做过的题目进行解答。

7、对结果进行预测

写一个predict预测函数，来对结果进行预测。在每一层中都要进行一个运算，l_out = A(l_in ×w+ b)。最后的预测结果就是l_out。

def predict(img,parameters):
	#对输入和输出进行初始化
    l_in=img#数据集里的图片作为第0层的输入
    l_out=activation[0](l_in)
    #通过一个for循环不断把上一层的输出作为下一层的输入，最后在进行输出
    for layer in range(1,len(dimensions)):#第0层没有参数，所以从第1层开始
        l_in=np.dot(l_out,parameters[layer]['w'])+parameters[layer]['b']
        l_out=activation[layer](l_in)
    return l_out

预测一下：

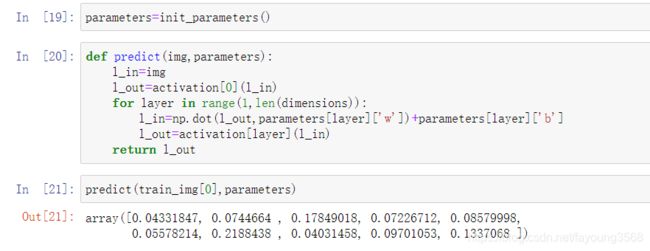
这里我们预测是训练集中的第0张图片在初始参数下的结果。一共是十个数字分别代表结果是数字0~9的概率。由此可以看出在这个参数下的对训练集中的图片预测结果是非常差的，什么数字都有可能出现。我们理想的结果应该是这样子的，十个数字，只有一个与标签对应的为1，其他的全为0。也就预测出来的数和图片上的数字是一定吻合的，没有其他数字的可能。

8、确定误差

我们已经看出这个误差的很大了，但现在我们要把这个误差具体是多少要算出来，以方便我们根据这个误差来对参数进行调整。在神经网络里对误差的计是是通过损失函数（Loss function） 进行的。损失函数有很多，这里为了方便，使用平方损失函数，就是将预测值和理想值之差再平方—(y-y_pred)^2。平方损失函数通过图片数据，标签，参数来确定误差。
代码如下：

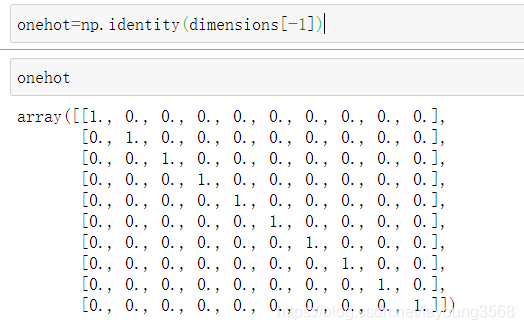
onehot=np.identity(dimensions[-1])

def sqr_loss(img,lab,parameters):
    y_pred=predict(img,parameters)
    y=onehot[lab]
    diff=y-y_pred
    return np.dot(diff,diff)#两个向量作内积，就是对应分量相乘再相加

onehot如下：

9、计算参数梯度

我们每一层（除了第0层）都有两个参数w和b。当输入值l_in确定时，预测结果l_out只有两个参数有关。通过改变两个参数，可以改变预测结果，使其符合我们的要求，也就是我们要根据预测结果和参数的关系找到预测结果的最低点使损失函数的值最小。这时就要预测结果l_out对两个参数分别求对应的偏导数，也叫做梯度。
注意：这里有多个激活函数，所以要进行复合函数求偏导。l_out（i） = A(l_in(i-1) ×w(i)+ b(i))。就是对l_out 递归求偏导。如果对参数b(i-1)求偏导，那就是w(i)×d_ l_in (i-1)×d_A(l_in(i-1) ×w(i)+ b(i)).

def grad_parameters(img,lab,parameters):
	#因为是多层神经网络，用列表存储输入和输出
    l_in_list=[img]
    l_out_list=[activation[0](l_in_list[0])]
    for layer in range(1,len(dimensions)):
    	#上一层的输入作为输出
        l_in=np.dot(l_out_list[layer-1],parameters[layer]['w'])+parameters[layer]['b']
        l_out=activation[layer](l_in)
        l_in_list.append(l_in)
        l_out_list.append(l_out)
    #对y_pred求偏导的公因式。(y-y_pred)^2
    d_layer=-2*(onehot[lab]-l_out_list[-1])
    
    #对每一层的参数初始化，即层数个None
    grad_result=[None]*len(dimensions)
    #range(start, stop, step)，从start到stop,每次加step
    for layer in range(len(dimensions)-1,0,-1):
    	#如果是第0层和第1层，运算符号是数乘
        if d_type[activation[layer]]=='times':
            d_layer=differential[activation[layer]](l_in_list[layer])*d_layer
        #如果是第2层，运算符号是内积
        if d_type[activation[layer]]=='dot':
            d_layer=np.dot(differential[activation[layer]](l_in_list[layer]),d_layer)
        grad_result[layer]={}
        grad_result[layer]['b']=d_layer
        grad_result[layer]['w']=np.outer(l_out_list[layer-1],d_layer)
        d_layer=np.dot(parameters[layer]['w'],d_layer)
    
    return grad_result

计算结果（一部分）如下：

除了第0层是None之外，其他两层的w和b都有值。

10、验证梯度的正确性

我们是根据计算的推导结果写出代码，但是推导错了怎么办？接下来就要对参数梯度进行验证。根据定义，验证1式-2式≈0就可以了。：

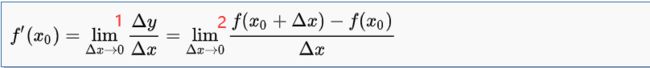
验证参数b（只需更改layer的值就可以验证不同层的参数b）:

#参数b
h=0.00001#Δx
layer=2#第几层
pname='b'#验证的参数
grad_list=[]
for i in range(len(parameters[layer][pname])):
    img_i=np.random.randint(train_num)
    test_parameters=init_parameters()
    derivative=grad_parameters(train_img[img_i],train_lab[img_i],test_parameters)[layer][pname]
    value1=sqr_loss(train_img[img_i],train_lab[img_i],test_parameters)
    test_parameters[layer][pname][i]+=h
    value2=sqr_loss(train_img[img_i],train_lab[img_i],test_parameters)
    grad_list.append(derivative[i]-(value2-value1)/h)
np.abs(grad_list).max()

b(1):

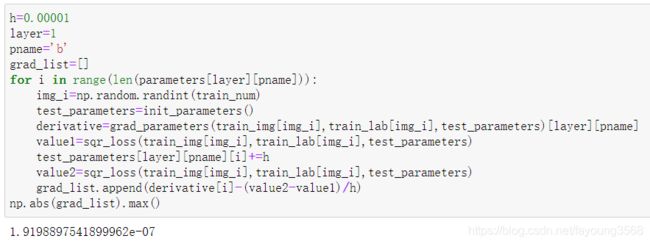
b(2):

验证参数w（只需更改layer的值就可以验证不同层的参数w）:

h=0.00001
layer=2
pname='w'
grad_list=[]
for i in range(len(parameters[layer][pname])):
    for j in range(len(parameters[layer][pname][0])):
        img_i=np.random.randint(train_num)
        test_parameters=init_parameters()
        derivative=grad_parameters(train_img[img_i],train_lab[img_i],test_parameters)[layer][pname]
        value1=sqr_loss(train_img[img_i],train_lab[img_i],test_parameters)
        test_parameters[layer][pname][i][j]+=h
        value2=sqr_loss(train_img[img_i],train_lab[img_i],test_parameters)
        grad_list.append(derivative[i][j]-(value2-value1)/h)
np.abs(grad_list).max()

w(1):

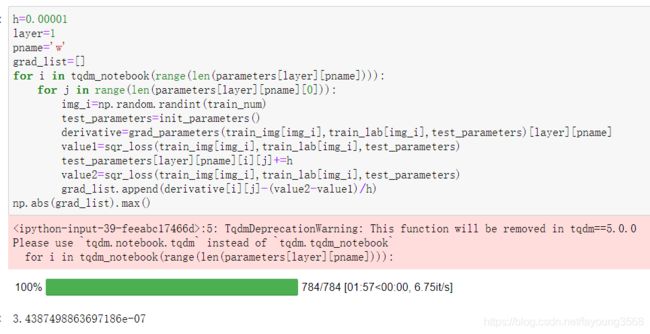
w(2):

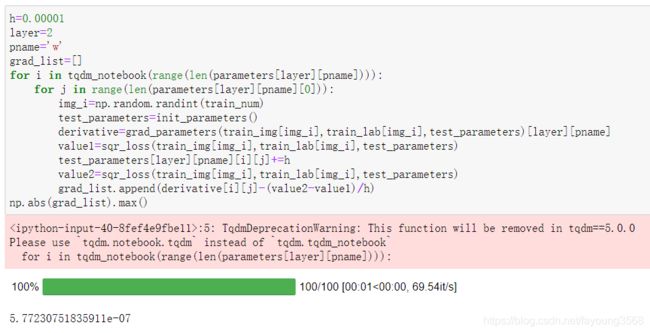
最后得出来的数值都是在10^-7量级，可以验证我们得出来的参数梯度是正确的，没有问题。

11、得到误差和精确度

现在我们有了数据、参数，就可以得到误差和进一步得到精确度。这里我们有三个小数据集，所以我们要得到这三个小数据集的误差和精确值。方便我们对参数进行一个综合分析。代码如下：

#训练集
def train_loss(parameters):
    loss_accu=0
    for img_i in range(train_num):
        loss_accu+=sqr_loss(train_img[img_i],train_lab[img_i],parameters)
    return loss_accu/(train_num/10000)
def train_accuracy(parameters):
    correct=[predict(train_img[img_i],parameters).argmax()==train_lab[img_i] for img_i in range(train_num)]
    return correct.count(True)/len(correct)
#验证集
def valid_loss(parameters):
    loss_accu=0
    for img_i in range(valid_num):
        loss_accu+=sqr_loss(valid_img[img_i],valid_lab[img_i],parameters)
    return loss_accu/(valid_num/10000)
def valid_accuracy(parameters):
    correct=[predict(valid_img[img_i],parameters).argmax()==valid_lab[img_i] for img_i in range(valid_num)]
    return correct.count(True)/len(correct)
#测试集
def test_accuracy(parameters):
    correct=[predict(test_img[img_i],parameters).argmax()==test_lab[img_i] for img_i in range(test_num)]
    return correct.count(True)/len(correct)
def test_loss(parameters):
    loss_accu=0
    for img_i in range(test_num):
        loss_accu+=sqr_loss(test_img[img_i],test_lab[img_i],parameters)
    return loss_accu/(test_num/10000)

12、对参数梯度进行处理

我们现在已经可以求出某一层的某一个参数了，而我们有多层多个参数，如果我们每训练一次就对单个参数进行处理，那要处理的数据就太多了。所以要对得到的梯度进行处理，并且是进行分组处理，以至于方便我们后续的处理数据。在这里我们是将每个小数据集分成了500组。
grad_add: 将得到的参数梯度进行一个累加。而为了方便处理数据，这个函数接收两个参数，我们使grad1=grad2+grad1
grad_divide: 将得到的参数进行一个平均化。因为我们得到的参数很多，累加起来数值很大，不方便我们使用，所以我们要把进行一个等比缩小，让数据更具有值观性。再这个方法中就是让各个参数除以其对应神经元的维数，也就是输入数据的个数。即grad=grad/demoninator。
train_batch： 运用上面两个参处理函数对训练集中每一组数据的参数进行处理，最后得到当前训练集中的平均化参数。
combine_parameters： 进行梯度下降。通过上面三个函数，我们可以对参数进行修改了，即梯度下降。parameter=parameter-learn_rate*grad。 这里的learn_rate指的是学习率，就是下降的幅度。如果默认学习率为1，那在一开始的时候，可能预测结果很好，但是当越来越接近最低点的时候，还按照之前的幅度下降，就有可能越过最低点，又上去了。所以，我们后面还要对学习率进行一个调整。
代码如下：

def grad_add(grad1,grad2):
    for layer in range(1,len(grad1)):
        for pname in grad1[layer].keys():
            grad1[layer][pname]+=grad2[layer][pname]
    return grad1
def grad_divide(grad,denominator):
    for layer in range(1,len(grad)):
        for pname in grad[layer].keys():
            grad[layer][pname]/=denominator
    return grad

batch_size=100
def train_batch(current_batch,parameters):
    grad_accu=grad_parameters(train_img[current_batch*batch_size+0],train_lab[current_batch*batch_size+0],parameters)
    for img_i in range(1,batch_size):
        grad_tmp=grad_parameters(train_img[current_batch*batch_size+img_i],train_lab[current_batch*batch_size+img_i],parameters)
        grad_add(grad_accu,grad_tmp)
    grad_divide(grad_accu,batch_size)
    return grad_accu

def combine_parameters(parameters,grad,learn_rate):
    parameter_tmp=copy.deepcopy(parameters)
    for layer in range(1,len(parameter_tmp)):
        for pname in parameter_tmp[layer].keys():
            parameter_tmp[layer][pname]-=learn_rate*grad[layer][pname]
    return parameter_tmp

13、训练

现在我们一切都准备就绪了，有了参数，有了梯度，就可以开始进行训练了。这里的epoch就是训练次数。我们每训练一次，参数梯度就下降一次。然后观察在训练过程中的误差变化和精确度的变化。由此来判断最佳参数是多少。首先要对参数进行一个初始化，然后通过list列表收集相对于的数据，方便作出图表。

#初始化参数
parameters=init_parameters()
#当前的训练次数
current_epoch=0
#收集各个小数据的误差和精度
train_loss_list=[]
valid_loss_list=[]
test_loss_list=[]

train_accu_list=[]
valid_accu_list=[]
test_accu_list=[]

#学习率
learn_rate=10**-0
#训练次数
epoch_num=1
#开始训练
for epoch in tqdm_notebook(range(epoch_num)):
    for i in range(train_num//batch_size):
        grad_tmp=train_batch(i,parameters)
        parameters=combine_parameters(parameters,grad_tmp,learn_rate)
    current_epoch+=1
    train_loss_list.append(train_loss(parameters))
    train_accu_list.append(train_accuracy(parameters))
    valid_loss_list.append(valid_loss(parameters))
    valid_accu_list.append(valid_accuracy(parameters))

我们先看一下在初始参数下训练集、验证集、测试集的精确度分别是多少？

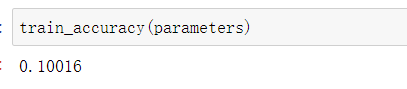
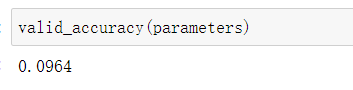
可以看出精确度都是在10%左右。这初始化的状态下，就差不多了。毕竟是10个里面选一个，就大概是十分之一的概率。并且我们可以看到精确度的大小排列是：测试集>训练集>验证集。这个结果是非常奇妙的。我们可以想一下，你在上完课后，写的课后作业的成绩还没有你考试的成绩好，所以可以说这个参数是有一点问题。那我们接下来训练一次看看训练效果，学习率就先设为1。训练代码如下：

learn_rate=10**-0
epoch_num=1
for epoch in tqdm_notebook(range(epoch_num)):
    for i in range(train_num//batch_size):
        grad_tmp=train_batch(i,parameters)
        parameters=combine_parameters(parameters,grad_tmp,learn_rate)
    current_epoch+=1
    train_loss_list.append(train_loss(parameters))
    train_accu_list.append(train_accuracy(parameters))
    valid_loss_list.append(valid_loss(parameters))
    valid_accu_list.append(valid_accuracy(parameters))

查看训练效果：

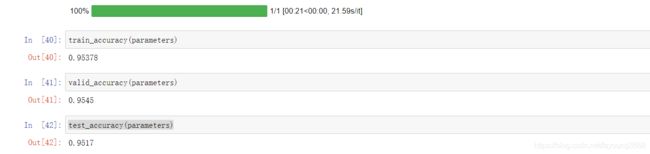
经过训练之后，我们可以看到精确度都有了非常显著的提高。这三者都达到了95%以上。说明经过训练之后，结果还是很好的。并且精确度结果是训练集>验证集>测试集这是符合我们的预期的。那我们在训练一次看看结果：

精确度还在提高。那我们接下来测试10次看看，并且我们把结果用图表的方式显示出来。只需将epoch_num=1改成10就可以了—epoch_num=10。代码如下：
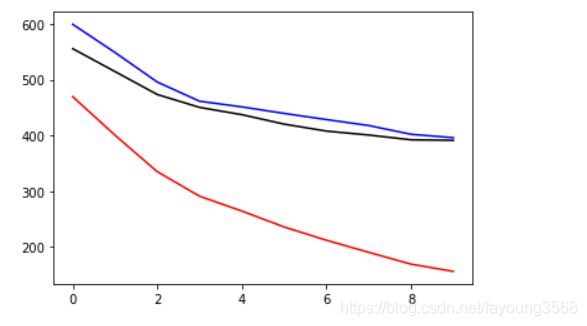
误差图表：

lower=-10
plt.plot(train_loss_list[lower:], color='red', label='train loss')
plt.plot(valid_loss_list[lower:], color='black', label='validation loss')
plt.plot(test_loss_list[lower:], color='blue', label='test loss')

plt.show()

精确度图表：

plt.plot(train_accu_list[lower:], color='red', label='train accuracy')
plt.plot(valid_accu_list[lower:], color='black', label='validation accuracy')
plt.plot(test_accu_list[lower:], color='blue', label='test accuracy')

plt.show()

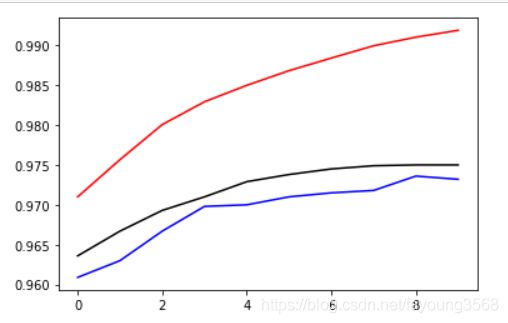
通过这两张图表我们可以看出，随着训练次数的增加，误差是越来越小，精确度是越来越大的。但是我们都可以看到他们都趋于水平了，甚至有下降的趋势。那我们接下来再看看训练一百次有什么效果？

14、100次训练

为了训练方便，大家可以直接把这个资料包里的训练模型modelv2_01.pkl导入到代码中，已经是提前训练好了100次，导入运行之后，直接看结果就可以了。在这里我们只研究训练集和验证集。可以把这个模型文件放在代码文件的同一级目录下。

path='modelv2_01.pkl'
with open(path,'rb') as f:
    (parameters,
        current_epoch,
        train_loss_list,
        valid_loss_list,
        train_accu_list,
        valid_accu_list
    )=pickle.load(f)

我们来看看结果：

精确度都非常高了，再看看图表是什么样子的。
先看完整的图表：
将lower=0
误差图表：

精确度图表：

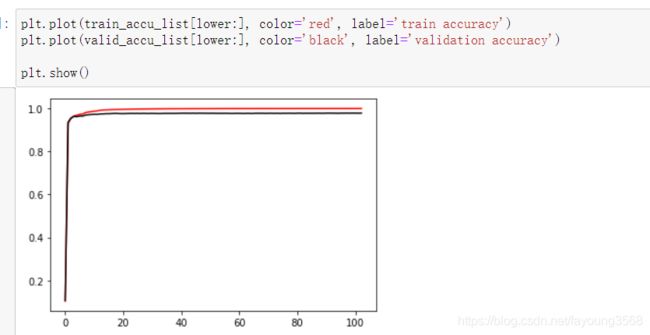
最后是趋于水平的，再看看最后20个数据。lower=-20
误差图表：

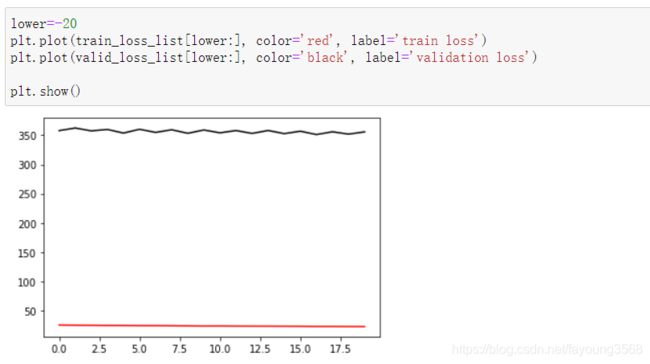
精确度图表：

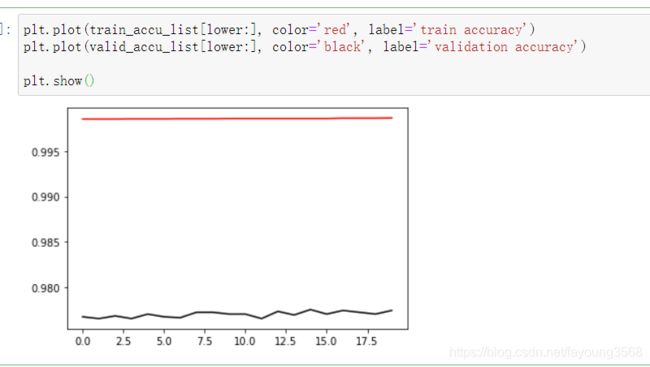
我们可以发现，测试集中的结果要比验证集中的效果好。这是一种过拟合现象。形象的说就是，在课堂上，对知识进行了一个很好的掌握，但是课后习题做的不太好。这是一种不好的现象。至于怎么解决这个问题，这涉及到很多因素。比如训练集的数量级和模型的复杂度不匹配、训练次数过多、训练集和测试集特征分布不一致等等。这属于进阶内容，入门的话只要有一个了解即可。

结尾：

到了现在，神经网络入门—手写识别已经全部完成了。希望我的博客可以对大家的学习有一定的帮助作用。接下来，我也将继续学习神经网络入门—猫狗大战部分，希望大家可以继续关注我的博客。

每日一句：生活是属于每个人自己的感受，不属于任何别人的看法