计算机视觉理论笔记 (4) - 图像质量和增强 (Image Quality & Enhancement)

总览

图像增强的目标在于生产一个比原图更"合适"的的图片。“合适”这个词在不同的应用中有不同的含义。

失真(distortion)和质量标准

图像捕获过程不可避免地会引入失真，从而降低图像质量。
视觉质量评估不足以用于计算机视觉应用。
图像质量应基于定量特征，这最终会影响对象识别和参数测量。

所有失真可以分为两类：

• 那些可以通过数字增强来纠正的。
• 那些无法通过数字增强校正并且需要优化成像过程的图像。

清晰度/锐度 (Sharpness)

清晰度决定图像可以清晰再现的细节量。
清晰度取决于几个因素：镜头质量，聚焦精度，传感器分辨率(传感器尺寸以像素为单位), CFA插值算法, 由于手抖导致的模糊。
相机制造商通常只宣传传感器分辨率。
清晰度的可测量参数是在垂直或水平方向上可以看到多少条黑白线。

图片缩放(调整大小)

下采样 (sub-sampling)

某些图像分析和对象识别操作不需要高分辨率图像。
图像尺寸可以通过下采样(sub-sampling)来减小。
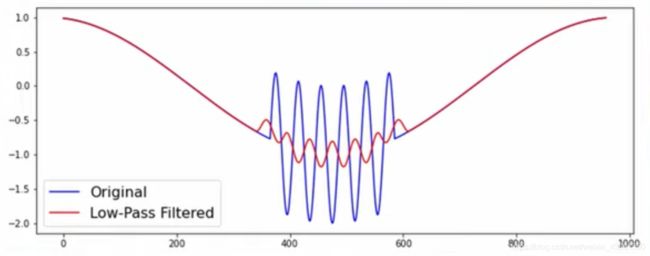
对图像进行直接下采样(去掉每第二个样本)很可能会违反采样定理(sampling theorem)而引入混叠。

采样定理 (the sampling theorem) : delta <= 1 / (2 * Fmax)
delta : 样本之间的间隔

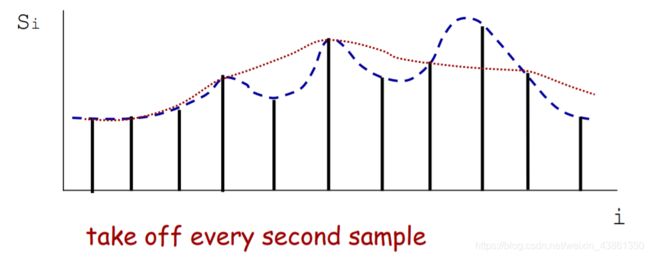
下采样：通过将每一个其他行和列丢弃从而创建一个相对原图1/2大小的图片。

混叠: 是指由于数字采样率不足而导致的信号频率测量错误。如果未使用足够的数据点对信号进行采样，则其真实频率将被低估。该错误估计的信号将与具有该真实较低频率的另一个信号无法区分。

如果Fmax = Fmax / 2，则下采样(sub-sampling)不会引起混叠。

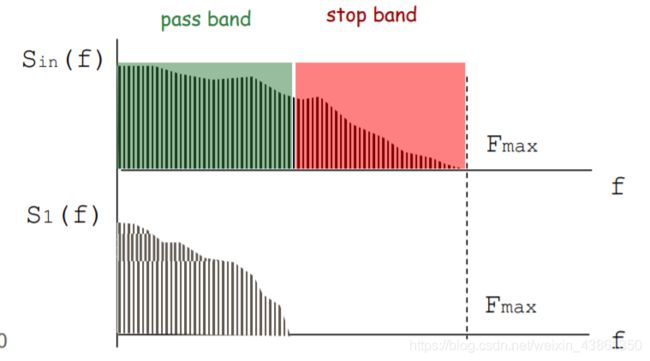
以N倍进行图像缩放的过程分为两个阶段
1.使用适当的频带限制滤波器将最大频率限制为Fmax / N
2.通过在N中仅保留一个样本来抽取图像

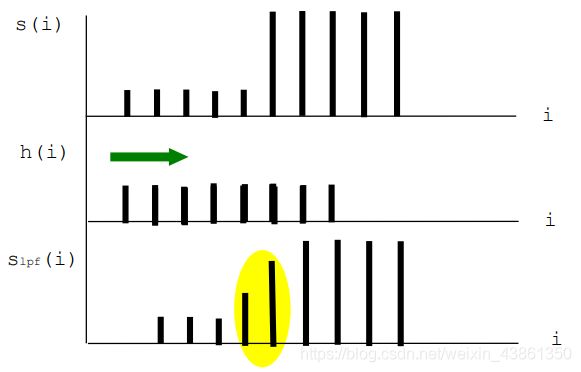
带限滤波器 (Band Limited Filter)

带限滤波器通常实现为线性运算，该线性运算使用输入样本的加权总和生成输出样本。

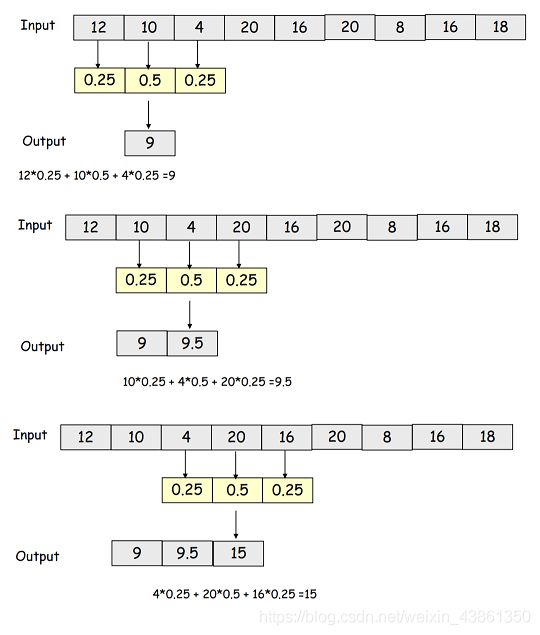
如图所示，这是个具有三个权重的带限低通滤波器(band limited low-pass filter)。滤波器对输入中的每三个数都进行运算并得出结果，该结果就是新输出的值。

滤波器 + 下采样

由于某些样本将被丢弃，因此可以将过滤和下采样过程结合起来以跳过不需要的位置

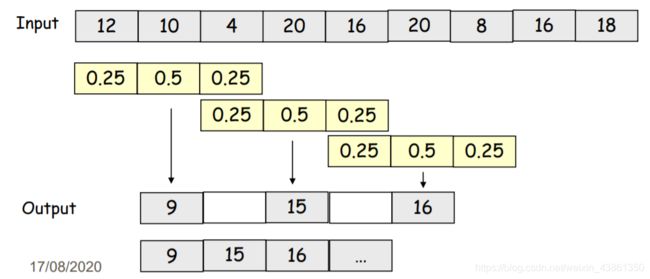
由于使用了下采样，因此滤波器的步长增加了。

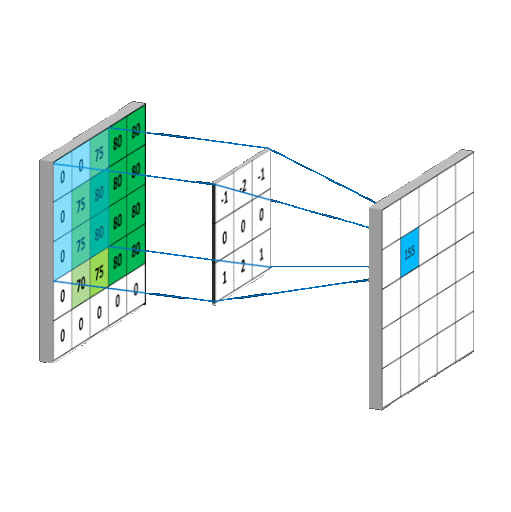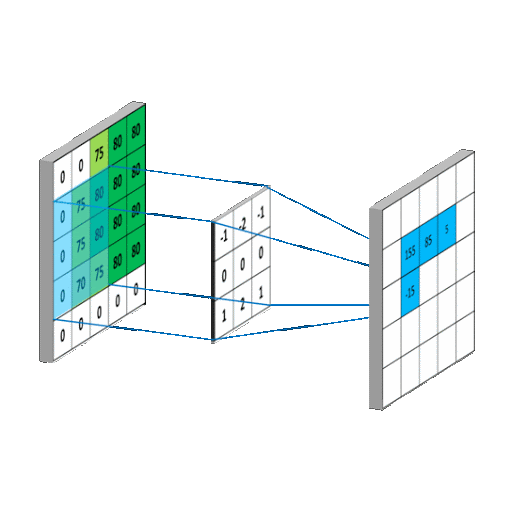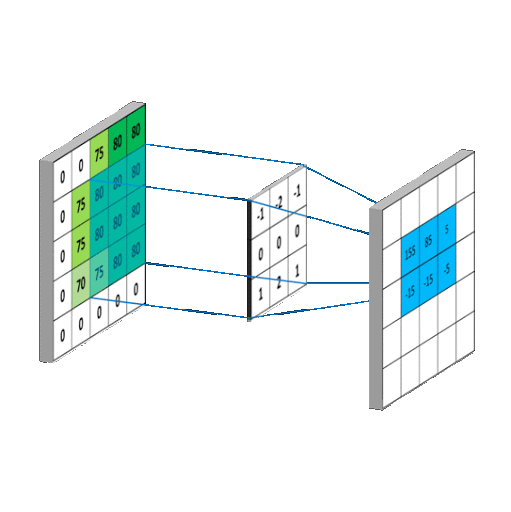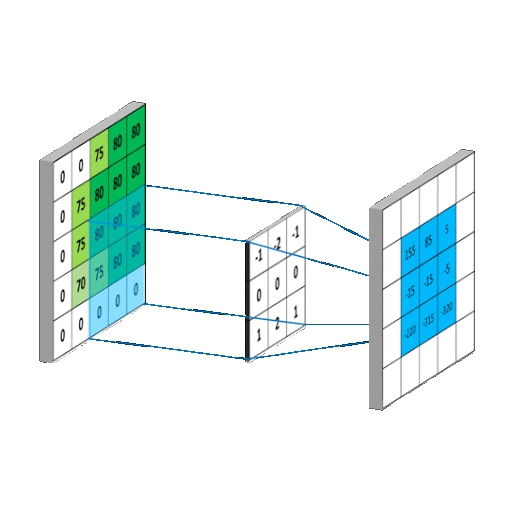
卷积(convolution)和2D低通滤波器

由于图像是样本的二维数组，因此会被二维滤波器过滤。二维滤波器是权重(滤波器系数)的二维数组。二维滤波器在图像上逐列逐行移动并生成处理后的输出图像。

步骤(循环执行)：

• 将滤波系数与相应的像素样本相乘，然后将结果相加，以生成滤波后的样本
• 将过滤后的样本放在输出图像中与过滤器中心当前位置相对应的位置
• 将过滤器移至下一个位置

颜色混叠 (Colour Aliasing)

具有Bayer模式的图像传感器的RGB分量以不同的速率采样。
而相机制造商通常会匹配G速率，即使这会导致R和B出现混叠。
颜色混叠无法消除，但可以通过CFA插值降低其可见性。(详见上一章)

对焦 (Focusing)

从理论上讲，当镜头聚焦到某个物体上时，与相机相距其他距离S的所有物体都无法聚焦。实际上，稍微靠近焦点的对象的前面和后面的对象也会显得相当清晰。 这种额外的深度称为景深(depth of field)。所有其他物体将模糊。

小的景深通常是艺术照片的理想功能，这用于强调感兴趣的物体并将其与背景隔离。计算机视觉相机可能需要较宽的景深，以便于分析复杂的场景。F-number越大，景深值越大。

焦外模糊

焦外模糊导致景深以外的所有物体的分辨率下降。焦外模糊以类似于低通滤波的方式影响图像。
数字图像处理可通过应用逆滤波器来提高图像清晰度，但副作用是会引入振铃效应。
振铃效应(ringing artifact)：所谓“振铃”，就是指输出图像的灰度剧烈变化处产生的震荡，就好像钟被敲击后产生的空气震荡。

运动模糊

运动模糊导致快速运动方向的分辨率下降。数字图像处理可以提高图像清晰度，但副作用是它同样会产生振铃效应。

饱和(Saturation)

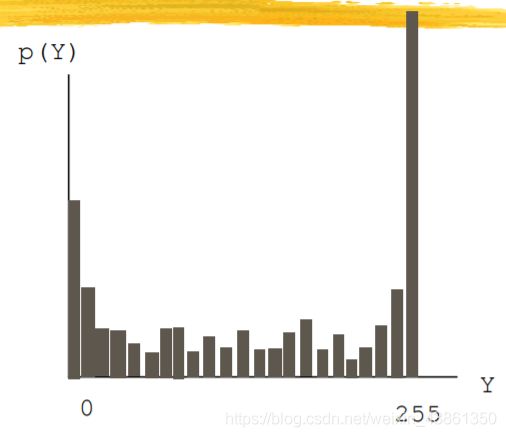
捕获高动态范围场景可能会导致饱和。
那些到达最大量化级别255的样本被裁剪，从而都变成了255的均匀区域，细节丢失了。

曝光不足

自动曝光 (auto-exposure) 和自动增益控制 (automatic gain control) 效率低下的数码相机可能会捕获未使用所有量化级别的图像，从而导致细节丢失。

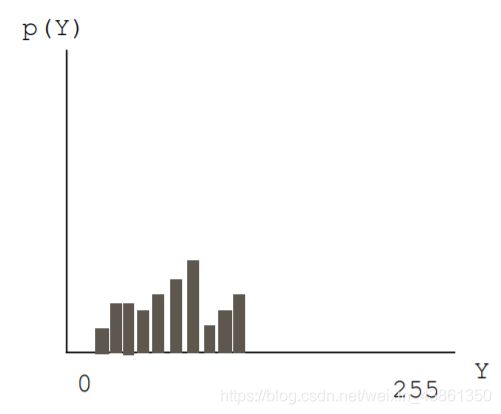
简单的对比度增强 (contrast enhancement) 仅改变图像的视觉外观，而使用相同数量的量化级别。

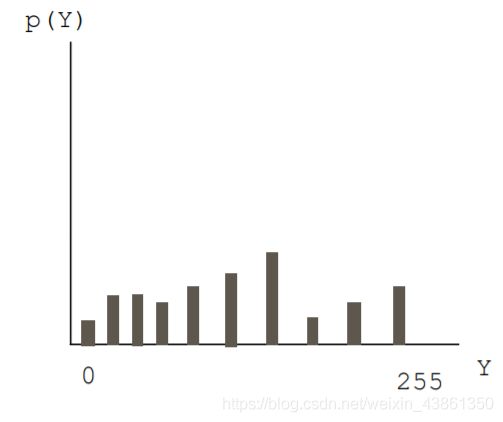
直方图

直方图是具有[0，L-1]范围内的灰度的图像的直方图(其中L通常为256)
其是离散函数 h® = n, 其中r是k级灰度值 ( 0 - 255), n是图像中拥有该灰度值的像素数量。
要归一化该直方图，我们需要让每个灰度级的n除以图片的总像素数。

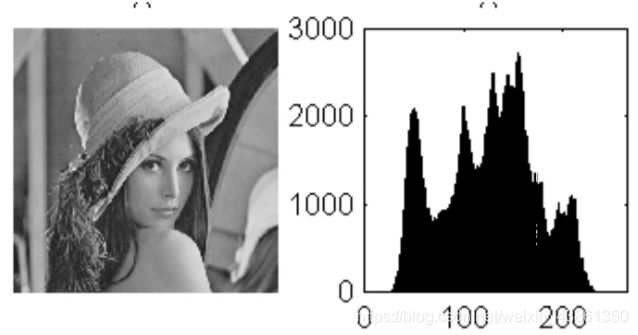
直方图均衡化/规格 (equalization / specification)

任何增强最终都会改变图像的颜色或强度分布。我们可以直接修改图像直方图来实现增强。

均衡化

均衡化：尝试使增强图像的直方图平坦，即利用所有可用的颜色/强度级别。目标是将图像直方图处理成第三张图的样子。

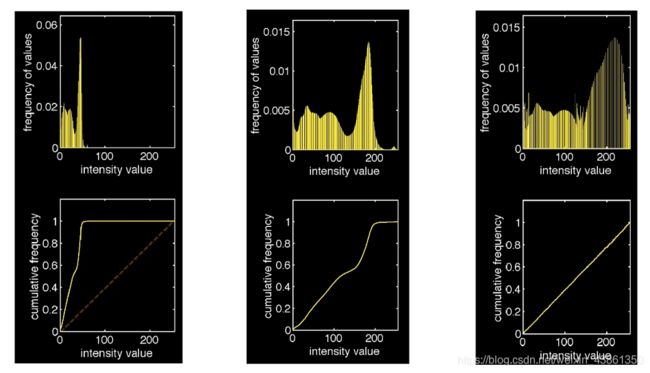
规格/匹配

规格/匹配：将图像的直方图修改为所需的直方图，令大多数观者感到满意。

光线

光源对颜色外观的影响以显色指数（CRI）表示，范围为0-100。 天然室外光的CRI为100，可作为其他任何光源的比较标准。

噪声

数码相机是一种除数字之外还包含模拟组件的电子设备。接收和处理目标信号会受到电流的随机波动，电子电路参数的随机变化以及来自其他电子组件的干扰的影响。噪声是一个随机过程，因此无法通过与影响图像质量的其他因素类似的方式消除，例如：分辨率，失焦 (defocus)，色彩保真度 (colour fidelity)，曝光不足 (under-exposure) 等。不采用统计和概率论就不可能降低噪声。

噪声源

• 光子散粒噪声 (photon shot noise) – 像素太小，以至于吸收的光子数量波动。
• 数字电路开关噪声 (digital circuit switching noise) – 来自数字电路的干扰。
• 固定模式噪声 (fixed pattern noise) – 不同像素的灵敏度略有不同。
• 热噪声 (thermal noise) – 取决于温度的电流波动。
• 量化噪声 (quantisation noise) – 量化导致的舍入误差。

噪声表示

噪声是一个随机过程，因此只能从统计学角度进行描述。其他统计参数也表征噪声，如均值和标准差。不同类型的噪声具有不同的概率密度。
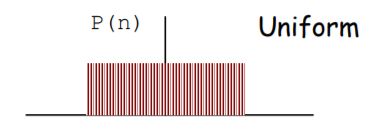
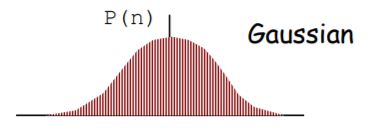
有两种最常见的概率密度：

1. Uniform (均匀分布)
   

2. Gaussian (高斯分布)
   
   Webber’s law：当一图片和另一图片的差异达到2％以上，人们就能意识到其差异。

量化噪声

量化噪声的均匀概率密度在[0…delta]的区间内。
若使用舍入 (truncation) 代替截断 (rounding)，则区间为[-delta/2 … delta/2]

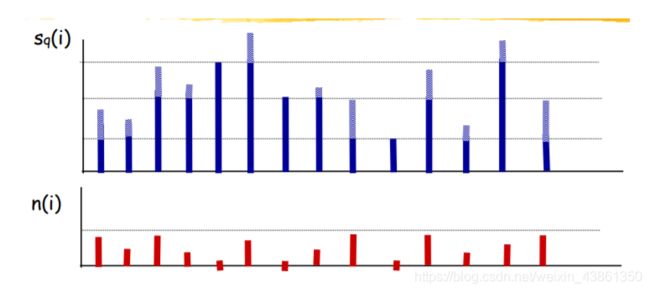
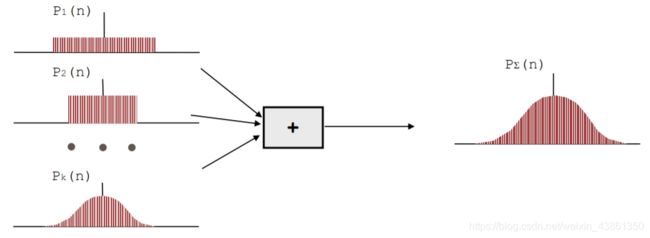
中心极限定理

大量独立随机过程的总和将具有大致的高斯概率密度。由于图像噪声来自多个独立来源，因此其分布近似为高斯分布，其中均值 = 0。

噪音模型

图像质量分析，图像处理和图像增强算法基于以下模型：均值为0的高斯分布噪声会添加到图像样本中。

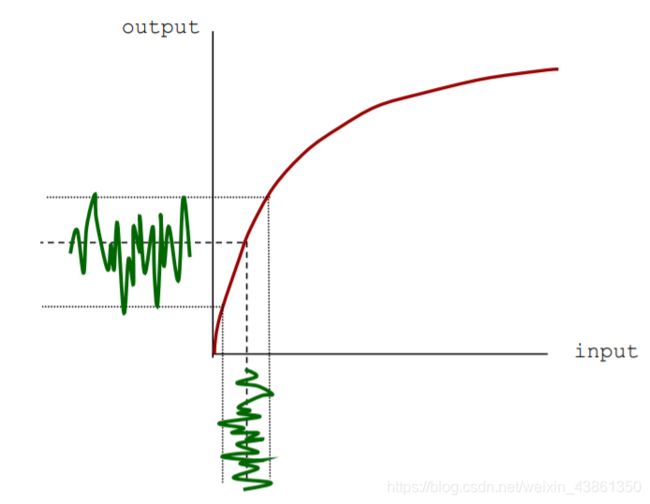
Gamma校正和噪声

Gamma校正的非线性会导致低照度的图像区域中的噪声放大。

颜色校正和噪声

提高色彩还原的准确性色彩校正会放大噪音。由于色彩校正是线性运算且噪声是加法运算，因此我们可以独立分析噪声传播。

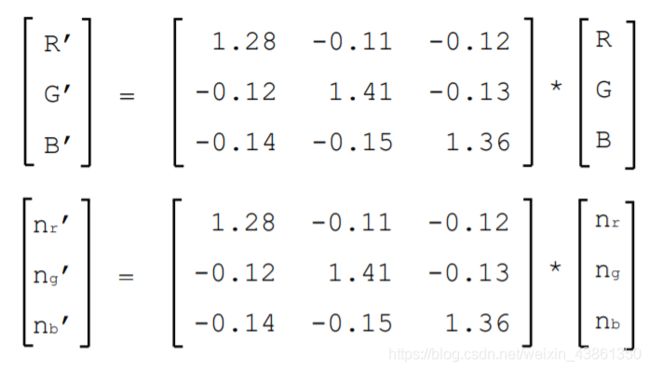
为了简化分析，我们做出两个假设：

1. 三个颜色通道R，G，B中的噪声在统计上是独立的（这对于带有Bayer模式传感器的相机并不严格正确）
2. R，G，B通道中的噪声标准偏差相同（对于配备Bayer模式传感器的摄像机来说，这不是严格正确的）

图片光谱

频域图像处理的基本步骤。首先图片原始信号f(x,y)会通过傅里叶变换转成傅里叶频谱F(u,v), 接着经过滤波操作。之后再通过反向傅里叶变换为增强的图片信号。

傅里叶变换 (Fourier Transform)

数学论证较为复杂，详见大神李永乐老师的讲解。

傅立叶变换如何理解？美颜和变声都是什么原理？李永乐老师告诉你

在图像中主要用途是将不规则的图像信号转化为傅里叶变换图 (连续频率分量，相位，频率)。同样，也可以有反向操作。将傅里叶变换图转换会原图像信号。

性质

• 对图片原始信号f(x,y)进行卷积操作和向其傅里叶转换结果做卷积操作是等价的。(给定核为h(x,y))。
• 自然图像的主要成分具有平滑的亮度和色彩变化，因此空间频率较低。
  由于人类拿相机倾向于水平或者垂直地拍摄目标景象，因此通常对角频谱分量通常弱于水平和垂直分量。
• 图像白噪声的空间频谱（即零均值，有限方差）是二维的（水平–垂直），例如 高斯白噪声。
  F(u, v)是图像f(x, y)的频谱，而N(u, v)是噪声n(x, y)的频谱，
  则 f(x, y) + n(x, y) = F(u, v) + N(u, v) (这是频谱表示的线性)

在频域中滤波

步骤：

1. 计算图片 f(x, y) 的 F(u, v).
2. 设计滤波函数 H(u, v)
3. 计算 G(u, v) = F(u, v)H(u, v)
4. 计算G(u, v)的反向傅里叶结果为滤波后或者处理后的图片。

根据通过图像光谱的哪个部分以及抑制光谱的哪个部分，可以将所有滤镜分为几组。

1. 低通滤波器。(low pass filter)
   低通滤波器倾向于找到高频信号并进行平滑和去噪。(因此低频信号就通过了)
   

• 0-1 低通滤波器
• Butterworth低通滤波器
• 高斯低通滤波器

2. 高通滤波器。(high pass filter)
   高通滤波器的一个经典应用场景就是边缘检测或者锐化。当我们使用高通滤波时，我们真正关心的是我们图片信号在哪里改变的最多(高频信号)。高频信号会通过，低频信号会接近0。
   

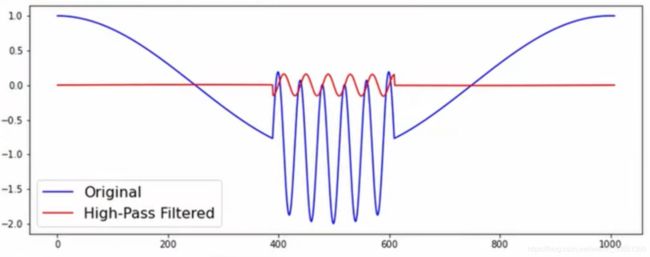
• 普通高通滤波器
• Butterworth高通滤波器
• 高斯高通滤波器

3. 带通滤波器。(band pass filter)
4. 带阻滤波器。(band stop filter)

作为典型的自然图像频谱，低频成分占主导地位。因此可以使用低通滤波器来除噪。 当滤波器的所有权重的总和等于1，滤波器不会影响图像的平均亮度。
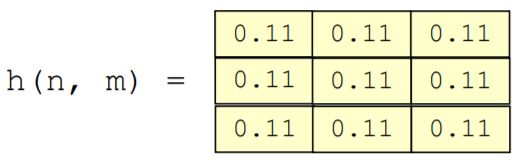
下图展现几种常用的Low pass filter - LPF内核，它们结合了合理的噪声抑制特性和较低的实现复杂性。

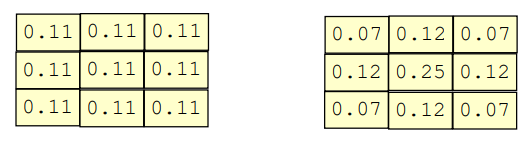
缺陷：LPF抑制噪声，也会影响图像。如果图像包含对象的锐利边缘 (sharp edges)，则它们会变得模糊。

理想的噪声抑制滤波器必须
1.有效降低噪音水平，尤其是在均匀区域。
2.不要模糊物体边缘。

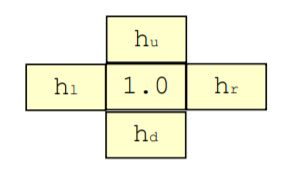
Anisotropic Diffusion是一种自适应滤波器，可避免跨对象边界进行LP滤波。其根据相邻图像像素在相应方向上的差异计算权重h。

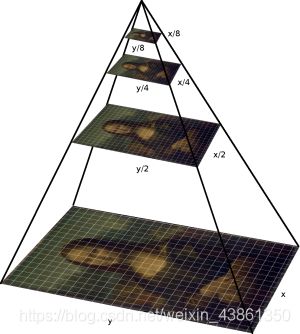
图像金字塔

图像在不同比例下可能看起来完全不同。 一种强大而简单的结构通常在计算机视觉图像金字塔中被使用，它以一种以上的分辨率表示图像。

高斯图像金字塔 (Gaussian Image Pyramids)

对某图像应用高斯低通滤波，并将滤波后的图像降采样2倍。如此循环以得到高斯图像金字塔。