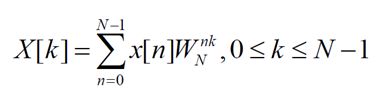基2FFT算法matlab程序编写,基2时抽8点FFT的matlab实现流程及FFT的内部机理

前言

本来想用verilog描述FFT算法，虽然是8点的FFT算法，但写出来的资源用量及时延也不比调用FFT IP的好，

还是老实调IP吧，了解内部机理即可，无需重复发明轮子。

参考

流程

FFT能做什么在此就不赘述了，只了解数据的运算流程。

1.FFT的基本公式：

第一眼看这个公式，肯定是脑袋瞬间宕机。

2.旋转因子：记住旋转因子具有可约性，对称性，周期性。

表示方法有两种，通过欧拉公式转换，本质上是一致的。

Wn=exp(-j*2*k*pi/N) ，N表示FFT点数，k表示第几个旋转因子。

Wn = cos(2*pi*k/N) - i*sin(2*pi*k/N)

第二次脑袋瞬间宕机。

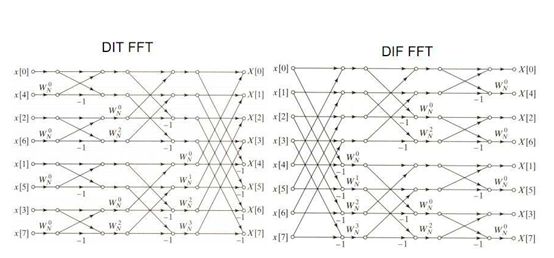
3.蝶形图：

好在数学家为了普通人类能理解公式，绘制了帅气的蝴蝶漫画图，8点FFT的如下：

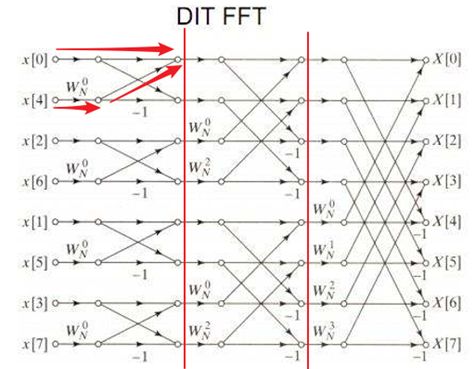
不直观，添加几条辅助线再看：可以看到分为三级蝶形运算。

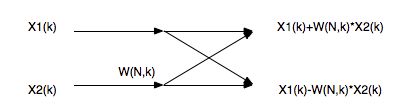
比如第一级的蝶形运算结果：x0’=x[0]+x[4]*w0,x1’=x[0]-x[4]*w0。其他节点以此类推。

注意-1的位置和旋转因子的位置。注意数据和旋转因子都是复数，这就是说蝶形图中的乘法和加减都是复数运算。

而所谓代码实现，不管什么代码，本质上就是对各级的公式进行实现，从而得到结果。

觉得讲得不清楚，那么看下图更直观：当然图中少标识了-1。

4.数据输入倒序：

从上图左侧可以看到，序列按照了一定的规则进行了倒序，如果按照顺序进行数据输入，肯定是不正确的。十进制可能看不出来，但使其转换为二进制表示就可以知道：

5.Matlab验证算法：

到这一步，就可以把蝶形结构用matlab语言描述出来了。蝶形因子进行了2^16次放大，数据经过了两级放大，结果需除去放大因子。

x序列为fs=500hz采样下的125hz且有直流分量的8点采样信号。

clc;

clear all;

close all;

%放大了2^16次的系数

w0 = ;

w1 = - *i;

w2 = -*i;

w3 = - - *i;

% w0 = ;

% w1 = 0.7071 - 0.7071*1i;

% w2 = -1i;

% w3 = -0.7071 - 0.7071*1i;

x = [,,,-,,,,-];

%%第一级蝶形运算,没有放大

x1()=x()+x();

x1()=x()-x();

x1()=x()+x();

x1()=x()-x();

x1()=x()+x();

x1()=x()-x();

x1()=x()+x();

x1()=x()-x();

%%第二级蝶形运算放大了65536，因为系数放大了2^，其他部分应当相应的放大

x2()=x1()*+x1()*;

x2()=x1()*+x1()*(w2);

x2()=x1()*-x1()*;

x2()=x1()*-x1()*(w2);

x2()=x1()*+x1()*;

x2()=x1()*+x1()*(w2);

x2()=x1()*-x1()*;

x2()=x1()*-x1()*(w2);

%%第三级蝶形运算放大了65536，因为系数放大了2^，其他部分相应的进行放大

y()=x2()*+x2()*;

y()=x2()*+x2()*(w1);

y()=x2()*+x2()*(w2);

y()=x2()*+x2()*(w3);

y()=x2()*-x2()*;

y()=x2()*-x2()*(w1);

y()=x2()*-x2()*(w2);

y()=x2()*-x2()*(w3);

% plot(abs(y/(^))-abs(fft(x)))

figure;

plot(x);

title('x value');

figure;

plot(abs(y/(^)));

title('旋转因子放大取整计算结果');

figure;

plot(abs(fft(x)));

title('matlab自带fft函数计算结果');

6.查看一下劳动成果：可以看到matlab自带的FFT和手动蝶形算出的FFT结果是一致的。

7.转成verilog描述，无非就是对各级的蝶形公式进行相关的实现。

注意：(1)乘法和加减法为复数运算。

(2)各级位宽需要注意，避免溢出。

看到蝶形图及相关公式，可以看到还是有点算法复杂度的。

虽然可以手敲实现，但FPGA厂商已经提供了足够好用的FFT IP core，资源量和计算延迟都很nice，

所以还是老实用IP吧。哈哈

8.FFT的一些性质：

(1)采样速率和点数的关系：

频谱分辨率△f=fs/N。点数和采样速率共同决定了FFT的频谱分辨率。

某一个点的频率关系：f=k*fs/N。注意FFT计算结果的第一点为直流分量。

(2)栅栏效应及补零处理：

频谱分辨率决定了透过栅栏窗子看真实频谱的真实度。补零可使得离散谱外观更加平滑，同时增长序列长度。

(3)FFT变换后的频域模幅度对应关系：

FFT计算出的第0个点为直流分量，其模值为直流分量的N倍。其余位置求得的模值需要除以N/2，才为真实的模值。

第0点：模值/N

其他频率点:模值/(N/2)

(4)频域幅度及相位计算：

某点(im,re)的幅度信息为：sqrt(im^2+re^2)，即实部平方加虚部平方开根号。

相位为：atan(im/re)，反三角算即可，即为本频谱时域的初相。

以上。

Matlab计算的FFT与通过Origin计算的FFT

实验的过程中,经常需要对所采集的数据进行频谱分析,软件的选择对计算速度影响挺大的.我在实验过程中,通常使用Origin7.5来进行快速傅里叶变换,因为方便快捷,计算之后,绘出来的图也容易编辑.但是当数 ...

多项式函数插值：全域多项式插值(一)单项式基插值、拉格朗日插值、牛顿插值 [MATLAB]

全域多项式插值指的是在整个插值区域内形成一个多项式函数作为插值函数.关于多项式插值的基本知识,见“计算基本理论”. 在单项式基插值和牛顿插值形成的表达式中,求该表达式在某一点处的值使用的Horner嵌 ...

Matlab周期图法使用FFT实现

参考文章:http://www.cnblogs.com/adgk07/p/9314892.html 首先根据他这个代码和我之前手上已经拥有的那个代码,编写了一个适合自己的代码. 首先模仿他的代码,测试 ...

FFT教你做乘法(FFT傅里叶变换)

题目来源:https://biancheng.love/contest/41/problem/C/index FFT教你做乘法 题目描述 给定两个8进制正整数A和B(A和B均小于10000位),请利用 ...

对AM信号FFT的matlab仿真

普通调幅波AM的频谱,大信号包络检波频谱分析 u(t)=Ucm(1+macos t)cos ct ma称为调幅系数 它的频谱由载波,上下边频组成 , 包络检波中二极管截去负半周再用电容低通滤波,可 ...

将caffe训练时loss的变化曲线用matlab绘制出来

1. 首先是提取 训练日志文件; 2. 然后是matlab代码: clear all; close all; clc; log_file = '/home/wangxiao/Downloads/43_ ...

几种快速傅里叶变换(FFT)的C++实现

链接:http://blog.csdn.net/zwlforever/archive/2008/03/14/2183049.aspx一篇不错的FFT 文章,收藏一下. DFT的的正变换和反变换分别为( ...

Xilinx FFT IP v9.0 使用(一)

reference:https://blog.csdn.net/shichaog/article/details/51189711 https://blog.csdn.net/qq_36375505/ ...

随机推荐

webpack练手项目之easySlide(一)：初探webpack (转)

最近在学习webpack,正好拿了之前做的一个小组件,图片轮播来做了下练手,让我们一起来初步感受下webpack的神奇魅力.     webpack是一个前端的打包管理工具,大家可以前往:http:/ ...

IE 下JS和CSS 阻塞后面内容总结

总结: 1.  CSS 都是可以并行下载的. 2.  IE6 和 IE7   JS 不能并行下载,CSS 和 JS 阻塞后面内容下载. 3.  IE8   JS 还是会阻塞图片下载 开始改变加载模式, ...

Bootstrap的学习以及简单运用

柠檬学院

How a non-windowed component can receive messages from Windows -- AllocateHWnd

http://www.delphidabbler.com/articles?article=1 Why do it? Sometimes we need a non-windowed componen ...

Linux性能监控分析命令

vmstat sar iostat top free uptime netstat ps strace lsof

iOS GCD 与 NSOperationQueue

NSOperationQueue ios NSOperation vs. GCD StackOverflow: NSOperation vs. Grand Central Dispatch Blog: ...

关于Servlet会话跟踪的那些事儿

关于servlet会话跟踪,一搜都能搜出很多.我也不免落入俗套,也总结了一把.希望我所总结的知识尽量是知识海洋里的一汪清泉.能帮助到我自己和哪怕一个人,那也是值得的. 故事由来: 我们知道,http协 ...

find grep

grep grep -rn "hello,world!" * #递归查找当前目录下所有包含hello,world的文件 grep -C number pattern files : ...

java的JCombobox实现中国省市区三级联动

源代码下载:点击下载源代码 用xml存储中国各大城市的数据. xml数据太多了就不贴上了,贴个图片: 要解释xml,添加了一个jdom.jar,上面的源代码下载里面有. 解释xml的类: packag ...

Mac 系统下创建可双击执行文件，cd到执行文件当前目录

在mac下之前我一直用.sh文件,但是要去终端里才能执行,后来得知可以写.command文件,双击及可执行,很方便,特此记录 #!/bin/bash basepath=$(cd `dirname $0 ...