构建智能系统：概率图开篇，机器学习中的图论总结(附思维导图)

0 写在前面

机器学习强基计划聚焦深度和广度，加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理；“广”在分析多个机器学习模型：决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。

详情：机器学习强基计划(附几十种经典模型源码合集)

---

概率图模型的知识体系非常庞大，在机器人、计算机视觉、推荐系统等领域应用广泛且难度较高，本专栏作为机器学习入门教程重点讲解概率图的基础概念。

本节介绍什么是概率图以及机器学习中的图论基础。

---

1 智能系统的三大组件

表示、推断和学习是构建智能系统的三个关键组件

• 表示(representation)是对真实世界的建模，主要以计算机可读的形式，合理编码关于系统运行的知识；
• 推断(inference)：很多任务需要智能系统利用已有的观测和先验知识去逻辑性地获得一系列当前未知的结论，这个过程称为推断；
• 学习(learning)：是从数据中产生模型的过程。基于数据学习，模型应提供对累积经验和专家先验知识的较优近似

机器学习模型都涉及上述三大组件中的至少一种。

2 什么是概率图？

概率图模型(Probabilistic Graphical Model, PGM)是以概率论、图论为理论基础，以局部随机变量条件独立性为核心，统一表示、推断、学习三大智能组件的灵活框架。

概率图模型用节点表示一个或一组随机变量，节点之间的边表示随机变量间的概率依赖关系。

概率图模型按图类型可分为两类：

• 有向无环概率图——常用于表示随机变量间显式的因果关系，经典的有向概率图为贝叶斯网络；
• 无向概率图——常用于表示随机变量间存在相关性但不易表示因果性的场合，经典的无向概率图为马尔科夫随机场

概率图模型的主要技术总结如下。

3 图论知识清单

图论中的图与欧式几何的概念不同，其主要用于表征某类具体事物及这些事物间的联系。图论的内容非常丰富，不可能通过一篇文章涵盖，以下通过思维导图的方式介绍最基础的概念，帮助大家快速入门。

3.1 无向图

无向图(Undirected Graph)定义为一个有序二元组，记为$G=\left(V,E\right)$，其中

• $V\ne \oslash$ 称为顶点集，其元素称为顶点，$|V|$表示顶点数或阶数
• $E$是由$V$中的顶点组成的无序点对构成的集合，称为边集，其元素称为边，同一点对可在$E$中重复出现多次，$|E|$表示边数。

无向图的基本概念总结如下：

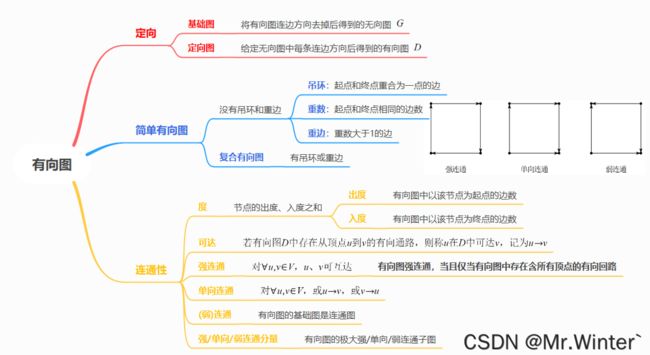
3.2 有向图

有向图(Directed Graph)基本定义与无向图一致，也是一个有序二元组$G=\left(V,E\right)$，只是$E$中元素称为弧，且对于边$e=⟨u,v⟩$，顶点$u$称为边$e$的起点或始点，$v$称为边$e$的终点。

有向图的基本概念总结如下：

3.3 树

树是连通的无圈图，其基本概念总结如下：

4 Python实现

基本方法继承自networkx库，不重复造轮子，但可以扩充或复写一些概率图的方法，比networkx库更适配机器学习模型，今后算法实验都采用这种方式。

4.1 继承nx.Graph

class DAG(nx.DiGraph):    
    def __init__(self, graph=None):
        super(DAG, self).__init__(graph)
        # DAG要求是无环图
        cycles = []
        try:
            cycles = list(nx.find_cycle(self))
        except nx.NetworkXNoCycle:
            pass
        else:
            out_str = "Cycles are not allowed in a DAG."
            out_str += "\nEdges indicating the path taken for a loop: "
            out_str += "".join([f"({u},{v}) " for (u, v) in cycles])
            raise ValueError(out_str)

4.2 添加节点和边

添加节点

def addNode(self, node, weight=None):
    super(DAG, self).add_node(node, weight=weight)

添加边

def addEdge(self, u, v, weight=None):
     super(DAG, self).add_edge(u, v, weight=weight)

4.3 可视化

network不提供这种方法，需要我们自己实现。

def plotGraph(self, highlight=None):
    from graphviz import Digraph
    nodeAttr = dict(
        align='left',
        fontsize='10',
        ranksep='0.1',
        height='0.2'
    )
    graph = Digraph(node_attr=nodeAttr, graph_attr=dict(size="12,12"))
    edges = self.edges()
    for u, v in edges:
        graph.edge(u, v)
    # 需要高亮的节点
    if highlight:
        for node in highlight:
            graph.node(node, style='filled', fillcolor='#b693fe')
    saveDir = os.path.abspath(os.path.join(__file__, "../../cache"))
    graph.view(filename='graph', directory=saveDir)

采用专门的绘图引擎可视化，不管是实验还是科研都非常有用。

完整代码联系下方博主名片获取

---

更多精彩专栏：

• 《ROS从入门到精通》
• 《机器人原理与技术》
• 《机器学习强基计划》
• 《计算机视觉教程》
• …

源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系