题目描述
题目链接:623. 在二叉树中增加一行
给定一个二叉树的根 root 和两个整数 val 和 depth ,在给定的深度 depth 处添加一个值为 val 的节点行。
注意,根节点 root 位于深度 1 。
加法规则如下:
- 给定整数
depth,对于深度为depth - 1的每个非空树节点cur,创建两个值为val的树节点作为cur的左子树根和右子树根。 cur原来的左子树应该是新的左子树根的左子树。cur原来的右子树应该是新的右子树根的右子树。- 如果
depth == 1意味着depth - 1根本没有深度,那么创建一个树节点,值val作为整个原始树的新根,而原始树就是新根的左子树。
提示:
示例 1:
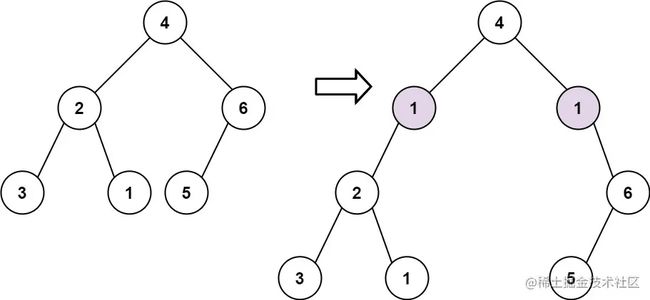
输入: root = [4,2,6,3,1,5], val = 1, depth = 2
输出: [4,1,1,2,null,null,6,3,1,5]
示例 2:
输入: root = [4,2,null,3,1], val = 1, depth = 3
输出: [4,2,null,1,1,3,null,null,1]
整理题意
题目给定一棵二叉树,要求我们在深度为 depth 的位置插入一行节点,这些节点的值为 val,题目规定根节点所在层位 1,且插入节点 val 的时候,原来节点的左子树要连接在新节点的左子树上,原来节点的右子树要连接在新节点的右子树上。
需要特别注意 depth = 1 的情况,此时将新节点作为根节点,将原来的根节点连接在新节点的左子树上。
解题思路分析
层序遍历(广度优先搜索)
根据题意描述,很容易想到使用 BFS 对整棵树进行层序遍历,在遍历到第 depth - 1 层时按照题意进行插入节点即可。
递归(深度优先搜索)
该题还可以通过给定的函数本身进行递归完成,在递归的过程中不断维护当前 depth 的值,当 depth 的值为 2 时进行节点的插入即可。
具体实现
常规的二叉树搜索,在对整棵二叉树进行搜索的同时维护当前树的深度即可,在第 depth 按照题意进行插入节点即可。
在实现过程中需要注意特判 depth = 1 的情况,也就是当插入的层数为 1 时,需要将根节点放在新插入节点的左子树上,并返回新插入的这个节点。
复杂度分析
- 时间复杂度:O(n),其中
n为输入的树的节点数。最坏情况下,需要遍历整棵树。 - 空间复杂度:O(n),在层序遍历中队列空间开销最多为 O(n),递归的深度最多为 O(n)。
代码实现
层序遍历(广度优先搜索)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* addOneRow(TreeNode* root, int val, int depth) {
// 特判 depth = 1 的情况
if(depth == 1){
TreeNode *res = new TreeNode(val);
res->left = root;
return res;
}
// k 记录当前层数
int k = 1;
queue que;
while(que.size()) que.pop();
que.push(root);
// bfs层序遍历
while(que.size()){
int n = que.size();
// 遍历到 depth - 1 层时开始插入元素 val
if(k == depth - 1){
for(int i = 0; i < n; i++){
TreeNode *now = que.front();
que.pop();
TreeNode *l = new TreeNode(val, now->left, NULL);
TreeNode *r = new TreeNode(val, NULL, now->right);
now->left = l;
now->right = r;
}
// 插入完成后跳出
break;
}
// 压入下一层节点元素
for(int i = 0; i < n; i++){
TreeNode *now = que.front();
que.pop();
if(now->left != NULL) que.push(now->left);
if(now->right != NULL) que.push(now->right);
}
k++;
}
return root;
}
};
递归(深度优先搜索)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* addOneRow(TreeNode* root, int val, int depth) {
if(root == nullptr) return root;
// 特判 depth = 1 的情况
if(depth == 1){
return new TreeNode(val, root, nullptr);
}
// 当 depth 到第 2 层时表示 在当前层的下一层插入节点 val
if(depth == 2){
root->left = new TreeNode(val, root->left, nullptr);
root->right = new TreeNode(val, nullptr, root->right);
return root;
}
// 否则一直递归
else{
root->left = addOneRow(root->left, val, depth - 1);
root->right = addOneRow(root->right, val, depth - 1);
}
return root;
}
};
总结
- 该题为常规的搜索题,既可以使用广度优先搜索进行层序遍历来完成,也可以使用深度优先搜索来递归完成,因为题目描述为插入一层元素节点,很容易想到层序遍历,而递归的方法较难想到,在实现过程中可以尝试使用递归的方式来完成,可以锻炼递归的思维以及在实现递归时的各种边界考虑。同时递归的代码也比层序遍历的代码更为简洁。
- 测试结果:
以上就是C C++ LeetCode题解在二叉树中增加一行示例详解的详细内容,更多关于C C++ 在二叉树中增加一行的资料请关注脚本之家其它相关文章!