【leetcode速通java版】01——数组入门

1.数组的基础理论

数组是在内存中空间连续的一块区域存储的某种数据类型的集合。

Q:java中二维数组在内存的空间地址是连续的么？

测试下

public static void test_arr() {
    int[][] arr = {{1, 2, 3}, {3, 4, 5}, {6, 7, 8}, {9,9,9}};
    System.out.println(arr[0]);
    System.out.println(arr[1]);
    System.out.println(arr[2]);
    System.out.println(arr[3]);
}

输出结果如下：

[I@7852e922
[I@4e25154f
[I@70dea4e
[I@5c647e05

上面的地址经过了处理，不过它们都没有规律，显然不连续。实际上，java的二位数组可能是这样的。

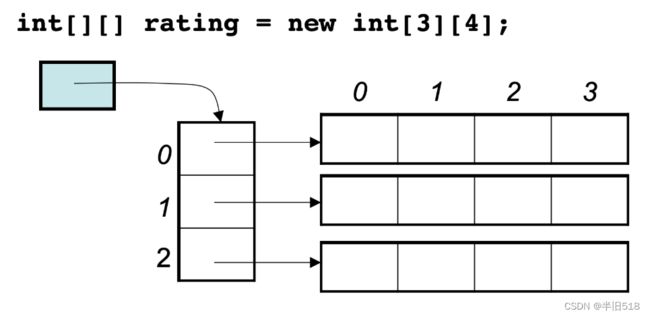
从这个角度，我们可以认为java中实际上不存在二维数组，因为二维数组不过是由一维数组链接而成的，并没有在地址空间上连续。

2.二分查找

分析：
这个题目要求对数组元素有序，同时给出了二分查找的两个条件，适用二分查找。
(1)数组是有序的
(2)数组元素不重复(一旦重复，则返回的结果可能是多个)

题解：

class Solution {
    public int search(int[] nums, int target) {
        // 注意第一次调用right为nums.length-1,而不是nums.length
        return BinarySearch(nums, target, 0, nums.length-1);
    }

    public int BinarySearch(int [] nums,int target, int left, int right) {
        if(left > right) {
            return -1;
        }
        int mid = (left + right)/2;
        if(nums[mid] == target) {
            return mid;
        } else if(nums[mid] < target) {
            return BinarySearch(nums, target, mid + 1, right);
        } else if(nums[mid] > target) {
            return BinarySearch(nums, target, left, mid-1);
        }

        return -1;
    }

上面的代码有两个return -1，不优雅，优化下。

class Solution {
    public int search(int[] nums, int target) {
        // 注意第一次调用right为nums.length-1,而不是nums.length
        return BinarySearch(nums, target, 0, nums.length-1);
    }

    public int BinarySearch(int [] nums,int target, int left, int right) {
        while(left <= right) {
            int mid = (left + right)/2;
             if(nums[mid] == target) {
                 return mid;
              } else if(nums[mid] < target) {
                 return BinarySearch(nums, target, mid + 1, right);
             } else if(nums[mid] > target) {
                 return BinarySearch(nums, target, left, mid-1);
         }

        }
     
        return -1;
    }
}

提升：
写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right),上面的解法是基于左闭右闭区间实现的。

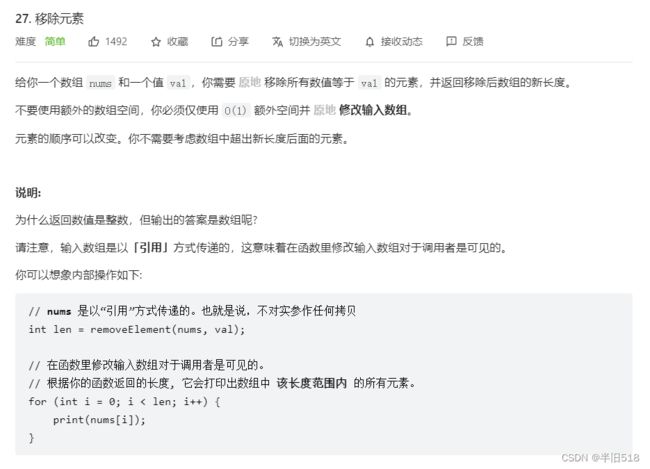
3 移除元素

知识点：
(1)算法原地工作
算法的实现只需要使用O(1)的空间，不需要额外的附加空间解决问题
(2)数组的元素在内存地址中是连续的，不能单独删除数组中的某个元素，只能覆盖。

法1：暴力解法
使用两层遍历，第一层用于查询，第二层用于更新元素。

class Solution {
    public int removeElement(int[] nums, int val) {
        int count = 0;
        for(int i = 0; i <  nums.length; i++) {
           if(nums[i] == val) {
               count++;
               for(int j = i; j < nums.length - 1; j++) {
                   nums[j] = nums[j+1];
               }
               i--; //所有元素往前移了，我们遍历索引也需要对应进行前一
           }
        }
        return nums.length - count;
    }
}

时间复杂度:O(n^2)
空间复杂度:O(1)
可见，该法的时间复杂度过高。

法2：快慢指针法
通过一个快指针和一个慢指针在一个for循环里完成两个for循环的操作。

定义快慢指针：
快指针：快速遍历原数组，寻找目标元素
慢指针：作为新数组的定位索引

class Solution {
    public int removeElement(int[] nums, int val) {
        int index = 0;
        for(int i = 0; i <  nums.length; i++) {
           if(nums[i] != val) {
               nums[index] = nums[i];
               index++;
           }
        }
        return index;
    }
}

时间复杂度：O(n)
空间复杂度：O(1)