【深度学习】Python实现CNN操作（附代码）

>参考： https://zhuanlan.zhihu.com/p/102119808 （可以直接看这个）

0 动机

通过普通的神经网络可以实现，但是现在图片越来越大，如果通过 NN 来实现，训练的参数太多。例如 224 x 224 x 3 = 150,528，隐藏层设置为 1024 就需要训练参数 150,528 x 1024 = 1.5 亿 个，这还是第一层，因此会导致我们的网络很庞大。

另一个问题就是特征位置在不同的图片中会发生变化。例如小猫的脸在不同图片中可能位于左上角或者右下角，因此小猫的脸不会激活同一个神经元。

CNN相较于全连接能够实现参数的共享。当使用一个具有9个卷积核、大小为5*5、步长为1的滤波器对一个大小为224 x 224 x 3 的图片进行卷积时，其参数量大小：(5 x 5+1) x 9 x 3 = 702
注： 不同通道之间的参数不共享。

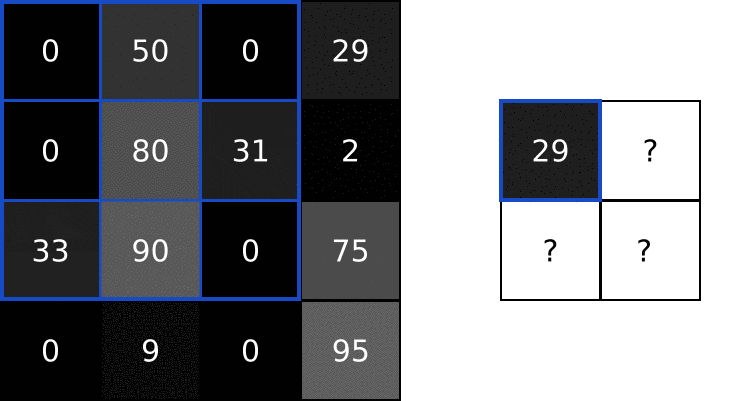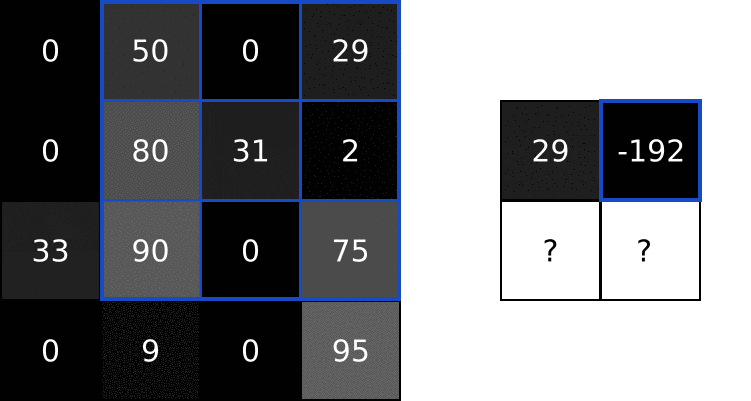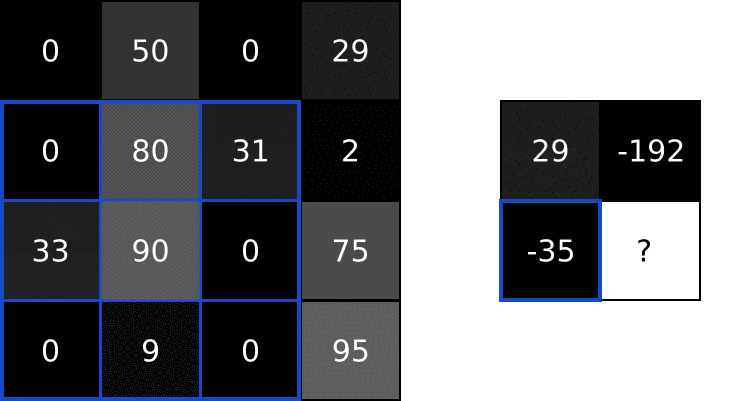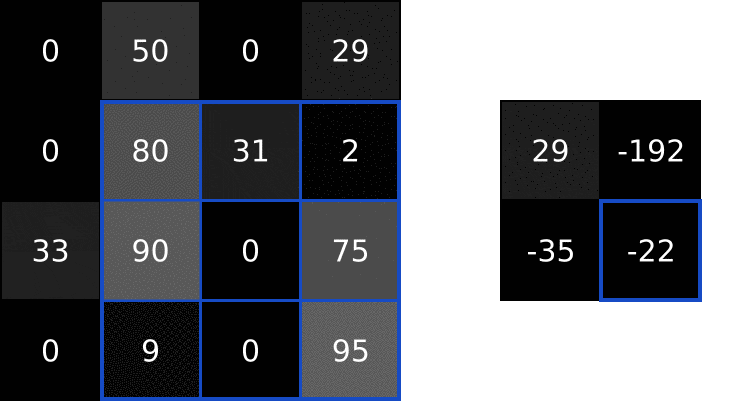
1. Conv

• Conv的原理示意图：
  

• 代码：

  class Conv3x3:
      # 卷积层使用3*3的filter.
      def __init__(self, num_filters):
          self.num_filters = num_filters
          self.filters = np.random.randn(num_filters, 3, 3) / 9       # 除以9是为了减小初始值的方差
          
      def iterate_regions(self, image):
          h, w = image.shape
          
          for i in range(h - 2):                                   # (h-2)/(w-2)是滤波以单位为1的步长，所需要移动的步数
              for j in range(w - 2):
                  im_region = image[i:(i + 3), j:(j + 3)]          # （i+3） 3*3的filter所移动的区域
                  yield im_region, i, j
                  
      def forward(self, input):
          # 28x28
          self.last_input = input
          
          h, w = input.shape
          output = np.zeros((h - 2, w - 2, self.num_filters))      # 创建一个（h-2）*（w-2）的零矩阵用于填充每次滤波后的值
          
          for im_region, i, j in self.iterate_regions(input):
              output[i, j] = np.sum(im_region * self.filters, axis=(1, 2))
              
          return output                                            # 4*4的矩阵经过3*3的filter后得到一个2*2的矩阵
      
      def backprop(self, d_L_d_out, learn_rate):
          # d_L_d_out: the loss gradient for this layer's outputs
          # learn_rate: a float
          d_L_d_filters = np.zeros(self.filters.shape)
          
          for im_region, i, j in self.iterate_regions(self.last_input):
              for f in range(self.num_filters):
                  # d_L_d_filters[f]: 3x3 matrix
                  # d_L_d_out[i, j, f]: num
                  # im_region: 3x3 matrix in image
                  d_L_d_filters[f] += d_L_d_out[i, j, f] * im_region
                  
          # Update filters
          self.filters -= learn_rate * d_L_d_filters
          
          # We aren't returning anything here since we use Conv3x3 as
          # the first layer in our CNN. Otherwise, we'd need to return
          # the loss gradient for this layer's inputs, just like every
          # other layer in our CNN.
          return None
  

2. MaxPool

• MaxPool的原理示意图：
  

• 代码：

  class MaxPool2:
      # A Max Pooling layer using a pool size of 2.
  
      def iterate_regions(self, image):
          '''
          Generates non-overlapping 2x2 image regions to pool over.
          - image is a 2d numpy array
          '''
          # image: 3d matix of conv layer
          
          h, w, _ = image.shape
          new_h = h // 2
          new_w = w // 2
  
          for i in range(new_h):
              for j in range(new_w):
                  im_region = image[(i * 2):(i * 2 + 2), (j * 2):(j * 2 + 2)]
                  yield im_region, i, j
  
      def forward(self, input):
          '''
          Performs a forward pass of the maxpool layer using the given input.
          Returns a 3d numpy array with dimensions (h / 2, w / 2, num_filters).
          - input is a 3d numpy array with dimensions (h, w, num_filters)
          '''
          # 26x26x8
          self.last_input = input
          
          # input: 3d matrix of conv layer
          h, w, num_filters = input.shape
          output = np.zeros((h // 2, w // 2, num_filters))
  
          for im_region, i, j in self.iterate_regions(input):
              output[i, j] = np.amax(im_region, axis=(0, 1))
          
          return output
          
      def backprop(self, d_L_d_out):
          # d_L_d_out: the loss gradient for the layer's outputs
          
          d_L_d_input = np.zeros(self.last_input.shape)
          
          for im_region, i, j in self.iterate_regions(self.last_input):
              h, w, f = im_region.shape
              amax = np.amax(im_region, axis=(0, 1))
              
              for i2 in range(h):
                  for j2 in range(w):
                      for f2 in range(f):
                          # If this pixel was the max value, copy the gradient to it.
                          if im_region[i2, j2, f2] == amax[f2]:
                              d_L_d_input[i + i2, j + j2, f2] = d_L_d_out[i, j, f2]
                              
          return d_L_d_input
  

3. Softmax

• Softmax的用法：
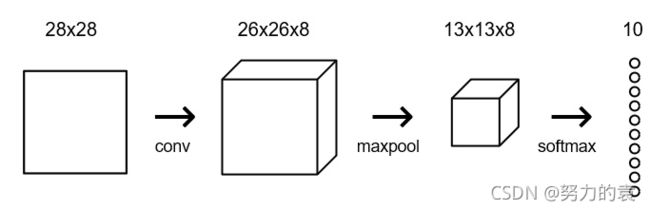
  使用一个含有 10 个节点（分别代表相应数字）的 softmax 层，作为 CNN 的最后一层。最后一层为一个全连接层，只是激活函数为 softmax。经过 softmax 的变换，数字就是具有最高概率的节点。
  

• 交叉熵损失函数（Cross-Entropy Loss）：
  

• 代码：

  class Softmax:
      # A standard fully-connected layer with softmax activation.
      
      def __init__(self, input_len, nodes):
          # We divide by input_len to reduce the variance of our initial values
          # input_len: length of input nodes
          # nodes: lenght of ouput nodes
          
          self.weights = np.random.randn(input_len, nodes) / input_len
          self.biases = np.zeros(nodes)
  
      def forward(self, input):
          '''
          Performs a forward pass of the softmax layer using the given input.
          Returns a 1d numpy array containing the respective probability values.
          - input can be any array with any dimensions.
          '''
          # 3d
          self.last_input_shape = input.shape
          
          # 3d to 1d
          input = input.flatten()
          
          # 1d vector after flatting
          self.last_input = input
  
          input_len, nodes = self.weights.shape
  
          totals = np.dot(input, self.weights) + self.biases
          
          # output before softmax
          # 1d vector
          self.last_totals = totals
          
          exp = np.exp(totals)
          return exp / np.sum(exp, axis=0)
      
      def backprop(self, d_L_d_out, learn_rate):
          # only 1 element of d_L_d_out is nonzero
          for i, gradient in enumerate(d_L_d_out):
              # k != c, gradient = 0
              # k == c, gradient = 1
              # try to find i when k == c
              if gradient == 0:
                  continue
          
              # e^totals
              t_exp = np.exp(self.last_totals)
          
              # Sum of all e^totals
              S = np.sum(t_exp)
              
              # Gradients of out[i] against totals
              # all gradients are given value with k != c
              d_out_d_t = -t_exp[i] * t_exp / (S ** 2)
              # change the value of k == c
              d_out_d_t[i] = t_exp[i] * (S - t_exp[i]) / (S ** 2)
          
              # Gradients of out[i] against totals
              # gradients to every weight in every node
              # this is not the final results
              d_t_d_w = self.last_input  # vector
              d_t_d_b = 1
              # 1000 x 10
              d_t_d_inputs = self.weights
          
              # Gradients of loss against totals
              # d_L_d_t, d_out_d_t, vector, 10 elements
              d_L_d_t = gradient * d_out_d_t
          
              # Gradients of loss against weights/biases/input
              # (1000, 1) @ (1, 10) to (1000, 10)
              d_L_d_w = d_t_d_w[np.newaxis].T @ d_L_d_t[np.newaxis]
              d_L_d_b = d_L_d_t * d_t_d_b
              # (1000, 10) @ (10, 1)
              d_L_d_inputs = d_t_d_inputs @ d_L_d_t
          
              # Update weights / biases
              self.weights -= learn_rate * d_L_d_w
              self.biases -= learn_rate * d_L_d_b
          
              # it will be used in previous pooling layer
              # reshape into that matrix
              return d_L_d_inputs.reshape(self.last_input_shape)
              
  # We only use the first 1k testing examples (out of 10k total)
  # in the interest of time. Feel free to change this if you want.
  test_images = mnist.test_images()[:1000]
  test_labels = mnist.test_labels()[:1000]
  
  # We only use the first 1k examples of each set in the interest of time.
  # Feel free to change this if you want.
  train_images = mnist.train_images()[:1000]
  train_labels = mnist.train_labels()[:1000]
  test_images = mnist.test_images()[:1000]
  test_labels = mnist.test_labels()[:1000]
  
  conv = Conv3x3(8)                    # 28x28x1 -> 26x26x8
  pool = MaxPool2()                    # 26x26x8 -> 13x13x8
  softmax = Softmax(13 * 13 * 8, 10)    # 13x13x8 -> 10
  
  def forward(image, label):
      '''
      Completes a forward pass of the CNN and calculates the accuracy and
      cross-entropy loss.
      - image is a 2d numpy array
      - label is a digit
      '''
      # We transform the image from [0, 255] to [-0.5, 0.5] to make it easier
      # to work with. This is standard practice.
      out = conv.forward((image / 255) - 0.5)
      out = pool.forward(out)
      out = softmax.forward(out)
  
      # Calculate cross-entropy loss and accuracy. np.log() is the natural log.
      loss = -np.log(out[label])
      acc = 1 if np.argmax(out) == label else 0
  
      return out, loss, acc
      
      # out: vertor of probability
      # loss: num
      # acc: 1 or 0
  

4. Train

• 训练概述：
  

• 代码:

  def train(im, label, lr=0.01):
      # Forward
      out, loss, acc = forward(im, label)
      
      # Calculate intial gradient
      gradient = np.zeros(10)
      gradient[label] = -1 / out[label]
      
      # Backprop
      gradient = softmax.backprop(gradient, lr)
      gradient = pool.backprop(gradient)
      gradient = conv.backprop(gradient, lr)
      
      return loss, acc
      
  print('MNIST CNN initialized!')
  
  
  # Train the CNN for 3 epochs
  for epoch in range(50):
      print('--- Epoch %d ---' % (epoch + 1))
      
      # Shuffle the training data
      permutation = np.random.permutation(len(train_images))
      train_images = train_images[permutation]
      train_labels = train_labels[permutation]
      
      # Train
      loss = 0
      num_correct = 0
      # i: index
      # im: image
      # label: label
      for i, (im, label) in enumerate(zip(train_images, train_labels)):
          if i > 0 and i % 100 == 99:
              print(
                  '[Step %d] Past 100 steps: Average Loss %.3f | Accuracy: %d%%' %
                  (i + 1, loss / 100, num_correct)
              )
              loss = 0
              num_correct = 0
  
          l, acc = train(im, label)
          loss += 1
          num_correct += acc
          
  # Test the CNN
  print('\n--- Testing the CNN ---')
  loss = 0
  num_correct = 0
  for im, label in zip(test_images, test_labels):
      _, l, acc = forward(im, label)
      loss += l
      num_correct += acc
  
  num_tests = len(test_images)
  print('Test Loss:', loss / num_tests)
  print('Test Accuracy:', num_correct / num_tests)
  

  结果：

  MNIST CNN initialized!
  --- Epoch 1 ---
  [Step 100] Past 100 steps: Average Loss 0.990 | Accuracy: 17%
  [Step 200] Past 100 steps: Average Loss 1.000 | Accuracy: 30%
  [Step 300] Past 100 steps: Average Loss 1.000 | Accuracy: 39%
  [Step 400] Past 100 steps: Average Loss 1.000 | Accuracy: 62%
  [Step 500] Past 100 steps: Average Loss 1.000 | Accuracy: 67%
  [Step 600] Past 100 steps: Average Loss 1.000 | Accuracy: 64%
  [Step 700] Past 100 steps: Average Loss 1.000 | Accuracy: 72%
  [Step 800] Past 100 steps: Average Loss 1.000 | Accuracy: 72%
  [Step 900] Past 100 steps: Average Loss 1.000 | Accuracy: 80%
  [Step 1000] Past 100 steps: Average Loss 1.000 | Accuracy: 77%
  --- Epoch 2 ---
  [Step 100] Past 100 steps: Average Loss 0.990 | Accuracy: 84%
  [Step 200] Past 100 steps: Average Loss 1.000 | Accuracy: 76%
  [Step 300] Past 100 steps: Average Loss 1.000 | Accuracy: 81%
  [Step 400] Past 100 steps: Average Loss 1.000 | Accuracy: 78%
  [Step 500] Past 100 steps: Average Loss 1.000 | Accuracy: 85%
  [Step 600] Past 100 steps: Average Loss 1.000 | Accuracy: 86%
  [Step 700] Past 100 steps: Average Loss 1.000 | Accuracy: 87%
  [Step 800] Past 100 steps: Average Loss 1.000 | Accuracy: 86%
  [Step 900] Past 100 steps: Average Loss 1.000 | Accuracy: 88%
  [Step 1000] Past 100 steps: Average Loss 1.000 | Accuracy: 77%
  --- Epoch 3 ---
  [Step 100] Past 100 steps: Average Loss 0.990 | Accuracy: 90%
  [Step 200] Past 100 steps: Average Loss 1.000 | Accuracy: 85%
  [Step 300] Past 100 steps: Average Loss 1.000 | Accuracy: 84%
  [Step 400] Past 100 steps: Average Loss 1.000 | Accuracy: 85%
  [Step 500] Past 100 steps: Average Loss 1.000 | Accuracy: 86%
  [Step 600] Past 100 steps: Average Loss 1.000 | Accuracy: 86%
  [Step 700] Past 100 steps: Average Loss 1.000 | Accuracy: 91%
  [Step 800] Past 100 steps: Average Loss 1.000 | Accuracy: 83%
  [Step 900] Past 100 steps: Average Loss 1.000 | Accuracy: 81%
  [Step 1000] Past 100 steps: Average Loss 1.000 | Accuracy: 82%
  
  --- Testing the CNN ---
  Test Loss: 0.5717330897439417
  Test Accuracy: 0.817