Q-Q图原理及Python实现
一、累积分布函数与分位数
累积密度函数（CDF，Cumulative Distribution Function）即概率密度函数的积分，公式如下：
分位数
是指满足 
的数，例如上四分位数是指累积概率达到75%时所对应的值。
二、Q-Q图的定义
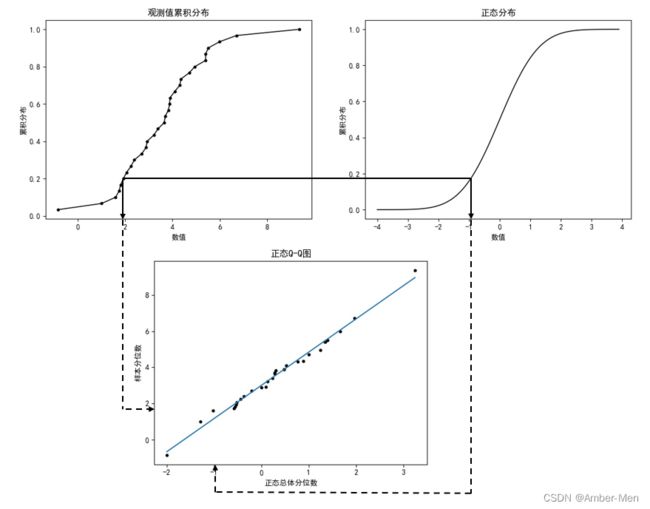
Q-Q图（Quantile-Quantile Plot，样本分位数-总体分位数）是一种散点图，它描述了样本分位数与观测值确实服从正态分布时所观察到的分位数之间的关系，可用来检验正态性假定是否成立。当各点近似分布在一条直线附近时，可认为正态性假设成立；反之，则不成立。
设
为某一随机变量
的n个观测值，这些观测值按大小排序后表示为
，由经验分布函数可知，
，
，为分析方便，作“连续性”修正，
近似为
(也可以近似为
，效果更好，R语言绘制的Q-Q图就是采用这种修正方法）
作Q-Q的步骤如下：
- 把原始观测值排序，得到
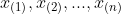和它们对应的概率值
,
,...,
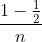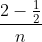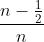
- 计算标准正态分位数
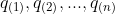，对于标准正态分布，分位数
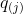由下述关系定义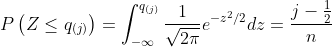
- 作观测值的点对(
),(
),...,(
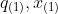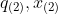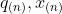)的图形，并检查结果的“直线性”（假设观测值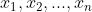服从正态分布，则
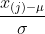服从标准正态分布，累积概率相同时，由Q-Q图可知
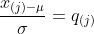，即
，由此可以看出若观测值近似服从标准正态分布，则各点应围绕
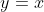波动）
三、Python实现
复刻一下大佬的图
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.distributions.empirical_distribution import ECDF
plt.figure(1)
x = np.arange(-4, 4, 0.1)
y = stats.norm.cdf(x, 0, 1)
plt.plot(x, y,c='k',lw=1.2)
plt.yticks(np.arange(0, 1.2, 0.2))
plt.xticks(np.arange(-4, 5, 1))
plt.xlabel('数值')
plt.ylabel('累积分布')
plt.title('正态分布')
# 样本数据随机取自均值为3，标准差为2的正态分布
mu, sigma = 3, 2
np.random.seed(10086)
data = np.random.normal(mu,sigma,size=30)
ecdf = ECDF(data)
cdf = ecdf(data)
data.sort()
cdf.sort()
plt.figure(2)
plt.scatter(data,cdf,c='k',s=10)
plt.plot(data,cdf,c='k',lw=1.2)
plt.xlabel('数值')
plt.ylabel('累积分布')
plt.title('观测值累积分布')
plt.figure(3)
mu, sigma = 0, 1
np.random.seed(12345)
x = np.random.normal(mu,sigma,size=30)
x.sort()
plt.scatter(x,data,c='k',s=10)
z = np.polyfit(x, data, 1)
f = np.poly1d(z)
# 绘制拟合线
plt.plot(x,f(x))
plt.xlabel('正态总体分位数')
plt.ylabel('样本分位数')
plt.title('正态Q-Q图')
plt.show() 
四、参考文献
实用多元统计分析：第6版 /（美）约翰逊（Johnson,R.A.），（美）威克恩（Wichern,D.W.）著；陆璇，叶俊译.
QQ图判断一个分布是否为正态分布_陋室逢雨的博客-CSDN博客_qq图怎么看正态分布