【动手学深度学习】3 Softmax 回归 + 损失函数

上一篇移步【动手学深度学习PyTorch版】2 线性回归_水w的博客-CSDN博客

 

目录

一、线性回归的简洁实现

1.1. 生成数据集

1.2. 读取数据集

1.3. 定义模型

1.4. 初始化模型参数

1.5. 定义损失函数

1.6. 定义优化算法

1.7. 训练

1.8. 小结

二、Softmax 回归

2.1. Softmax 回归

◼ 回归VS分类

# Kaggle分类问题

◼ 从回归到分类

2.2 交叉熵损失

2.3 总结

---

一、线性回归的简洁实现

1.1. 生成数据集

我们首先生成数据集，

1.2. 读取数据集

我们可以调用框架中现有的API来读取数据。 我们将features和labels作为API的参数传递，并通过数据迭代器指定batch_size。

此外，布尔值is_train表示是否希望数据迭代器对象在每个迭代周期内打乱数据。

​

为了验证是否正常工作，让我们读取并打印第一个小批量样本。 与之前不同，这里我们使用iter构造Python迭代器，并使用next从迭代器中获取第一项。 

​

1.3. 定义模型

我们实现线性回归时， 我们明确定义了模型参数变量，并编写了计算的代码，这样通过基本的线性代数运算得到输出。 但是，如果模型变得更加复杂，且当你几乎每天都需要实现模型时，你会想简化这个过程。 这种情况类似于为自己的博客从零开始编写网页。 做一两次是有益的，但如果每个新博客你就花一个月的时间重新开始编写网页，那并不高效。

对于标准深度学习模型，我们可以使用框架的预定义好的层。这使我们只需关注使用哪些层来构造模型，而不必关注层的实现细节。

我们首先定义一个模型变量net，它是一个Sequential类的实例。

Sequential类将多个层串联在一起。 当给定输入数据时，Sequential实例将数据传入到第一层， 然后将第一层的输出作为第二层的输入，以此类推。

在下面的例子中，我们的模型只包含一个层，因此实际上不需要Sequential。 但是由于以后几乎所有的模型都是多层的，在这里使用Sequential会让你熟悉“标准的流水线”。

回顾下图中的单层网络架构， 这一单层被称为全连接层（fully-connected layer）， 因为它的每一个输入都通过矩阵-向量乘法得到它的每个输出。​

在PyTorch中，全连接层在Linear类中定义。 值得注意的是，我们将两个参数传递到nn.Linear中。

• 第一个指定输入特征形状，即2，
• 第二个指定输出特征形状，输出特征形状为单个标量，因此为1。

​

1.4. 初始化模型参数

在使用net之前，我们需要初始化模型参数。 如在线性回归模型中的权重和偏置。 深度学习框架通常有预定义的方法来初始化参数。

在这里，我们指定每个权重参数应该从均值为0、标准差为0.01的正态分布中随机采样， 偏置参数将初始化为零。

正如我们在构造nn.Linear时指定输入和输出尺寸一样， 现在我们能直接访问参数以设定它们的初始值。 我们通过net[0]选择网络中的第一个图层， 然后使用weight.data和bias.data方法访问参数。 我们还可以使用替换方法normal_和fill_来重写参数值。

​

1.5. 定义损失函数

计算均方误差使用的是MSELoss类，也称为平方范数。 默认情况下，它返回所有样本损失的平均值。

​

1.6. 定义优化算法

小批量随机梯度下降算法是一种优化神经网络的标准工具， PyTorch在optim模块中实现了该算法的许多变种。 当我们实例化一个SGD实例时，我们要指定优化的参数 （可通过net.parameters()从我们的模型中获得）以及优化算法所需的超参数字典。 小批量随机梯度下降只需要设置lr值，这里设置为0.03。

​

1.7. 训练

通过深度学习框架的高级API来实现我们的模型只需要相对较少的代码。 我们不必单独分配参数、不必定义我们的损失函数，也不必手动实现小批量随机梯度下降。

当我们需要更复杂的模型时，高级API的优势将大大增加。 当我们有了所有的基本组件，训练过程代码与我们从零开始实现时所做的非常相似。

回顾一下：在每个迭代周期里，我们将完整遍历一次数据集（train_data）， 不停地从中获取一个小批量的输入和相应的标签。 对于每一个小批量，我们会进行以下步骤:

• 通过调用net(X)生成预测并计算损失l（前向传播）。

• 通过进行反向传播来计算梯度。

• 通过调用优化器来更新模型参数。

为了更好的衡量训练效果，我们计算每个迭代周期后的损失，并打印它来监控训练过程。​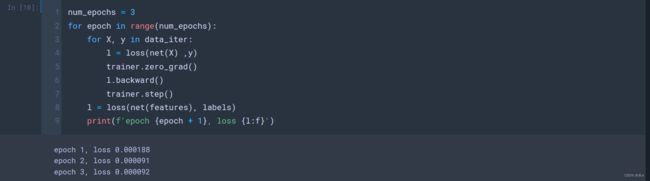

下面我们比较生成数据集的真实参数和通过有限数据训练获得的模型参数。

要访问参数，我们首先从net访问所需的层，然后读取该层的权重和偏置。

​

正如在从零开始实现中一样，我们估计得到的参数与生成数据的真实参数非常接近。 

1.8. 小结

• 我们可以使用PyTorch的高级API更简洁地实现模型。

• 在PyTorch中，data模块提供了数据处理工具，nn模块定义了大量的神经网络层和常见损失函数。

• 我们可以通过_结尾的方法将参数替换，从而初始化参数。

二、Softmax 回归

2.1. Softmax 回归

回归可以用于预测多少的问题。 比如预测房屋被售出价格，或者棒球队可能获得的胜场数，又或者患者住院的天数。

事实上，我们也对分类问题感兴趣：不是问“多少”，而是问“哪一个”：

• 某个电子邮件是否属于垃圾邮件文件夹？

• 某个用户可能注册或不注册订阅服务？

• 某个图像描绘的是驴、狗、猫、还是鸡？

• 某人接下来最有可能看哪部电影？

通常，机器学习实践者用分类这个词来描述两个有微妙差别的问题： 1. 我们只对样本的“硬性”类别感兴趣，即属于哪个类别； 2. 我们希望得到“软性”类别，即得到属于每个类别的概率。 这两者的界限往往很模糊。其中的一个原因是：即使我们只关心硬类别，我们仍然使用软类别的模型。

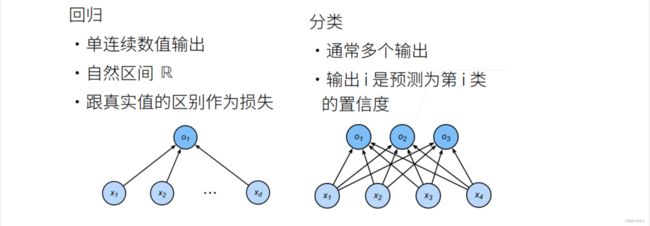
◼ 回归VS分类

• 回归估计一个连续值；
• 分类预测一个离散类别；

​

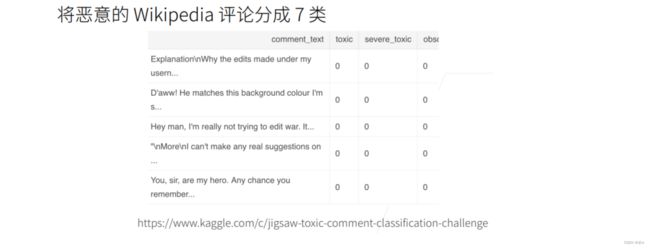
# Kaggle分类问题

​

​ 

​

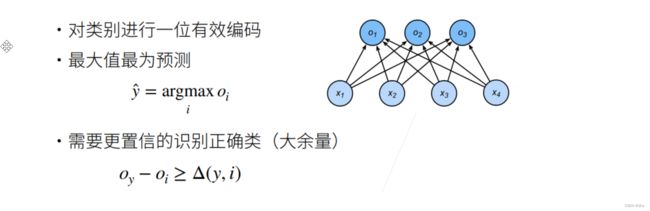
◼ 从回归到分类

​

假设我们有n个类别，那么我们的标号就是长为n的向量，从y1，y2......一直到yn。其中，假设我们的真实类别是第i个的话，那么我的yi就等于1，其他的元素全部都是等于0。所以就是说一位有效编码。

​

有了编码之后，我们其实可以用最简单的线性回归问题的均方损失来训练模型，我们就可以在不改动的情况下。

然后假设我们训练出来了一个模型，做预测的时候，那么我们就是选取i是的最大化的Oi，就是置信度的值，作为我的预测值y^，就是我们预测的一个标号。

接下来，我们看一下就是说怎么样从这个技术点一步一步过渡到我们真正的softmax回归。

​

就分类来讲，我们其实不关心它们之间的实际的值，我们关心的是说能不能够对正确类别的置信度特别大。比如我们可以将目标函数改成， 我们需要使得我们对正确类别y的置信度Oy要远大于其他非对正确类别的置信度，这样能够保证真正的正确类别y与其他类别区分开。这是我们最简单的一个想法。

另外我们一个想法是说：

虽然我们这里没有说具体的正确类别y的置信度Oy是什么样的值，大一点小一点都没关系，我们关系的是一个相对值。但是呢，如果我们把值放在一个合适的区间里，也会让我们后面的处理变得更加简单。

比如说，我们希望使得输出的能够是一个概率，现在我们的输出是一个向量（O1,O2,...On），我们可以引入一个新的操作子softmax，将softmax作用在O上，得到一个y^，它是一个长为n的向量，但是它每个元素都是非负的，且和为一。

​

这样的好处就是，我们的y^其实就是一个概率了。任何满足每个元素都是非负的，且和为一的都可以看成是一个概率。

那么我们就得到了两个概率，一个是真实的概率，一个是预测的概率。我们可以比较两个概率之间 的区别作为损失。

2.2 交叉熵损失

一般我们使用交叉熵损失用来衡量两个概率之间的区别，

​

如果我们把它当成损失的话，那么真实值y对预测值y^之间的损失就是l(y,y^)。这个损失的梯度其实就是真实概率和预测概率的区别。

2.3 总结

​