【机器学习】最经典案例：房价预测（完整流程：数据分析及处理、模型选择及微调）

环境：anaconda+jupyter notebook

数据处理前导：

首先要明白一点：
数据决定模型的上限！数据决定模型的上限！数据决定模型的上限！（重要的事情说三遍。）对于数据的处理在一个完整案例中花费精力的比重应该占到一半以上。
以下分为：数据分析、数据清洗两部分。
数据分析主要包括：查看数据内容（行列意义）、属性（数值型、类别型）、非空值数量、属性自身分布、属性之间的关联度、属性与预测目标值之间的关联度高低等。
数据清洗包括：1）数值型的缺省值处理办法、2）文本/类别型数据处理办法3）自定义处理数据方法、4）特征缩放处理、5）对于以上几种方法的封装

（一）、数据分析

这一部分你可以看成是操作数据的一些常用工具罗列，一些是必要的，一些是不必要的，但都可以帮助你更好的了解你的数据。

1、收集数据（必要）->2、查看数据（5个常用函数）->3、分割训练、测试数据（必要）->4、数据相关性及可视化

1、收集数据

创建一个小函数来实现实时下载数据包，不仅可以获取实时数据，而且很方便查看数据。

import os 
import tarfile
import urllib

DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml2/master/"
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz"#网址位置
HOUSING_PATH = os.path.join("datasets", "housing")#存储位置

def fetch_housing_data(housing_url = HOUSING_URL, housing_path = HOUSING_PATH):
    os.makedirs(housing_path, exist_ok = True)
    tgz_path = os.path.join(housing_path, "housing.tgz")
    urllib.request.urlretrieve(housing_url, tgz_path)
    housing_tgz = tarfile.open(tgz_path)
    housing_tgz.extractall(path = housing_path)#解压
    housing_tgz.close()
#调用
fetch_housing_data()

至此，已经下载好了数据集。

接下来，需要加载你下载好的数据，将数据的pandas DataFrame对象作为返回。

import pandas as pd

def load_housing_data(housing_path = HOUSING_PATH):
    csv_path = os.path.join(housing_path, "housing.csv")
    return pd.read_csv(csv_path)#返回 包含所有数据的pandas DataFrame对象
housing = load_housing_data()

至此，已经将数据加载到housing中，可以对housing进行一系列数据操作了。

2、查看数据结构

共介绍了5个常用函数，注释包含了每个函数实现的功能。

housing.head()#函数1：无参数时，默认查看前5行
#前面的列都是数值属性，最后一列是文字/类别属性

housing.info()#函数2：查看数据集属性描述（必要）
#如图所示：20640行*10列，列出每列的属性，非空值个数（total_bedrooms有空值），类型

housing.describe()#函数3：查看数值属性列的均值、最小最大值等信息

%matplotlib inline 
# 设置matplotlib使用jupyter自己的后端，随后在notebook 上呈现图形
import matplotlib.pyplot as plt
housing.hist(bins = 50, figsize = (20,15))#函数4：各属性各自的分布：即处于横轴区间（x轴）的样本个数为多少（y轴）
plt.show()

housing["ocean_proximity"].value_counts()#函数5：查看这个唯一的文本/类别属性ocean_proximity共有多少种分类

至此，我们用一些常用函数查看了数据的一些有用信息。

接下来，我们要划分数据集，分为训练集和测试集两份。测试集比例设为20%。

3、划分数据集

划分方式是灵活的，可以自定义划分数据集，或者调用sklearn提供的train_test_spllit（）方法都是可以的。但这种随机划分数据集的方式容易导致数据是有偏的，即存在验本偏差。（举个栗子：某地区一家公司要给1000个人打电话调研一些问题，已知该地区男女比例6:4，那么调查的样本中也应该包含6成男性、4成女性，否则将会存在抽样偏差。）

所以这里介绍分层抽样，一种常用的抽样方法：
分层抽样的前提是要直到对于样本分布的一个重要指标是什么（就像上面的例子中直到==知道该地区的男女比例很重要一样），那么从领域专家那里了解到收入中位数对于房价中位数的预测有重要作用。然而，收入中位数是一个连续值属性，需要先把它进行区间划分，转为类别属性，再从每个类中进行抽样。

#分层之前先摸底，查看完整数据集的分布
#专家说收入中位数是很重要的，按收入范围分成category
import numpy as np
housing["income_cat"] = pd.cut(housing["median_income"], bins = [0., 1.5, 3., 4.5, 6., np.inf], labels = [1, 2, 3, 4, 5])#创建5个收入分类，标签1-5
housing["income_cat"].hist()#显示收入类别直方图

至此，已经将income_cat属性从数值型转化为类别型。

接下来，需要进行分层抽样：

#开始抽样，显示抽样比例分布
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits = 1, test_size = 0.2, random_state = 42)
for train_index, test_index in split.split(housing, housing["income_cat"]):
    strat_train_set = housing.loc[train_index]#训练集
    strat_test_set = housing.loc[test_index]#测试集
#检验各个类别的比例分布
strat_test_set["income_cat"].value_counts()/len(strat_test_set)

至此，已经完成了分层抽样，将数据集划分为了strat_train_set、strat_test_set。

接下来，这个类别属性就用不到了，删掉即可：

#数据恢复原样，去掉income_cat属性
for set_ in (strat_train_set, strat_test_set):
    set_.drop("income_cat", axis = 1, inplace = True)

4、数据相关性可视化

首先拷贝一份训练数据集的副本，以免伤害原始数据。

#创建数据副本，防止伤害训练集                                                                                                                                                              
housing = strat_train_set.copy()

接下来，查看房价和地理位置（x,y）和人口密度s的关系：（图中横轴表示经度，纵轴表示维度，圆的半径大小代表了人口数量，颜色从蓝到红表示房价由低到高。）

#房价分布, s-蓝色-人口数量，c-颜色-价格-（蓝-红）
housing.plot(kind = "scatter", x = "longitude", y = "latitude", alpha = 0.4, 
             s = housing["population"]/100, label = "population", figsize = (10,7), 
             c = "median_house_value", cmap = plt.get_cmap("jet"), colorbar = True,
            )
plt.legend()

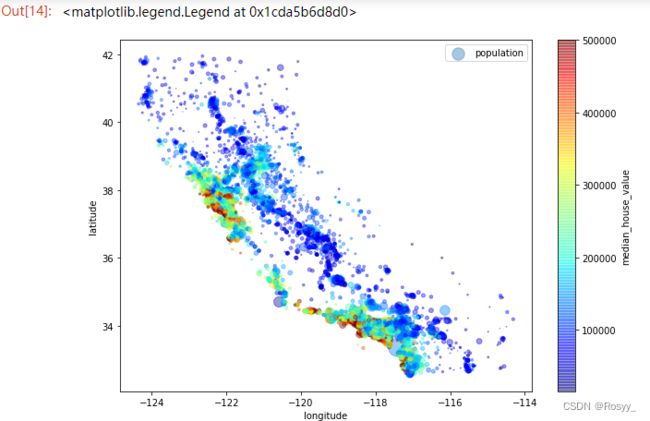
从图中可以初步判断：沿海地区的房价要偏高一些，当然也会受到人口等其他因素的影响。

接下来，寻找数据之间的相关性，这里主要查看房价与所有属性之间的相关性：

#计算每对属性的相关系数
corr_matrix = housing.corr()
#每个属性与房价中位数的相关系数
corr_matrix["median_house_value"].sort_values(ascending = False) 

可以看出前四行：median_income、total_rooms、housing_median_age与median_house_value的相关度还是挺高的。

接下来，看一下他们几个之间的相关性如何：

from pandas.plotting import scatter_matrix

attributes = ["median_house_value", "median_income", "total_rooms", "housing_median_age"]
scatter_matrix(housing[attributes], figsize = (12,8))

从图中可以看出median_house_value和median_income呈现较为明显的线性相关性。（也印证了：前文所说的从领域专家那里了解到房价和收入中位数有较强的相关性。）

接下来，我们从已有属性中创造一些新的属性，或许新的属性可以和房价之间有较好的相关性，这个相关系数或许会高于已知属性和房价的相关系数。

#几栋房/每家
#几个卧室/每栋房子
#几个人/每家
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"] = housing["population"]/housing["households"]
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending = False)

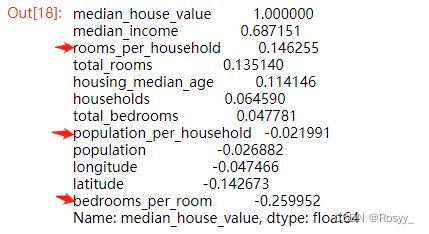
从结果上可以看出rooms_per_household比一些已有属性具有和房价更高的相关性。所以这个属性或许对我们之后的房价预测起到一定帮助。

（二）、数据清洗

前文介绍了很多关于数据的一些常规操作，这些操作一些是可选的，但可以帮助更好的理解数据。
接下来，是比较重要的数据清洗。
主要介绍几种方法适用于不同情况，最后介绍如何将这些清洗操作封装起来。（封装起来的目的是，训练集、测试集都需要执行清洗一系列操作，封装好可以直接调用，更加简洁）

1、缺失值

对于含有空值的列（如前文交代的total_bedroom列），通常可以采取3种方法：1）放弃缺失值相应的区域、2）放弃含缺失值的列、3）用中位数/0/均值来代替缺失值。
然而，前两种方法对于数据来说无疑是一种浪费，这里介绍如何用第三种方法，完成缺失值填补。
首先，还是将训练集拷贝下来，注意是训练集。
用drop()和copy()将数据集的标签分离出来，即分理出x,y。

#干净的训练集：预测器和标签分开，因为两者进行数据转换的方式不同。
housing  = strat_train_set.drop("median_house_value", axis = 1)#housing数据副本 只包含预测器（9列），不含标签
housing_labels = strat_train_set["median_house_value"].copy()
housing.info()

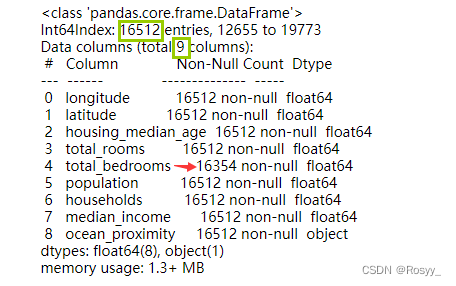
从结果中可以看到：训练集的x为16512*9的，其中total_bedrooms有空值。

接下来，开始用中位数填补空值：
根据sklearn提供的SimpleImputer类，很方便的用中位数填补空值。（助记：0.创建类1.fit() 2.transform()）

from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy = "median")#0.类
housing_num = housing.drop("ocean_proximity", axis = 1)#housing_num不含标签和ocean_proximity属性
imputer.fit(housing_num)#1.fit

X = imputer.transform(housing_num)#iii 缺失值替换成中位数，从而完成训练集转换结果numpy
housing_tr = pd.DataFrame(X, columns = housing_num.columns, index = housing_num.index)

# housing_num.info()#补好的数据存入了X, X再变成DataFrame存入housing_tr
housing_tr.info()

至此，已经填补好了数值类型的缺失值。

2、文本/分类属性

由于计算机没办法处理文本类型的属性，所以需要对其进行编码，转化为数学表达。常用的编码方式有：转化为数字类别，一种是转化为独热码。
如果转化为数字编码：从（一）数据分析->2、查看数据结构->函数5可知：ocean_proximity属性共有5种类别，即为0~4，但是这里引入了一个不友好的因素，就是数字相近的类别具有较高的相似度（通俗来说就是，一个样本如果在类别1或2之间徘徊，如果最后评分的时候把它归为了1类，但是它其实含有和类别2相似的因素。）
所以，这里介绍采用独热码的形式进行编码：
根据sklearn提供的OneHotEncoder类，很方便的用中位数填补空值。（助记：0.创建类1.fit() 2.transform()，1.2可以合并）

#  编码器，独热编码：生成独热向量
from sklearn.preprocessing import OneHotEncoder
housing_cat = housing[["ocean_proximity"]]##

cat_encoder = OneHotEncoder()#相当于类对象：含有方法：fit_transform，含有变量：categories_
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
housing_cat_1hot
# print(housing_cat_1hot[:10])
#转化为密集的numpy
housing_cat_1hot.toarray()

至此，完成了对文本/分类属性的编码。

3、自定义转换器

可以根据需要自定义一些转换器，来处理数据，把不论是任何形式的数据，最终都变成数学表达。
在此案例中主要用于处理我们后来新创建的几个联合属性。

from sklearn.base import BaseEstimator, TransformerMixin
rooms_ix, bedrooms_ix, population_ix, household_ix = 3,4,5,6
class CombinedAttributesAdder(BaseEstimator, TransformerMixin):#自定义转换器：CombinedAttributesAdder
    def __init__(self, add_bedrooms_per_room = True): #没有 *args, **kargs
        self.add_bedrooms_per_room = add_bedrooms_per_room
    def fit(self, X, y = None):
        return self
    def transform(self, X):
        rooms_per_household = X[:, rooms_ix]/X[:, household_ix]
        population_per_household = X[:, population_ix]/ X[:, household_ix]
        if self.add_bedrooms_per_room :
            bedrooms_per_room = X[:, bedrooms_ix]/ X[:, rooms_ix]
            return np.c_[X, rooms_per_household, population_per_household, bedrooms_per_room]
        else:
            return np.c_[X, rooms_per_household, population_per_household]
attr_adder = CombinedAttributesAdder(add_bedrooms_per_room = False)
housing_extra_attribs = attr_adder.transform(housing.values)

4、特征缩放

如果输入的数值属性具有较大的比例差异，那么非常必要将其进行缩放。
常用的缩放方法有：01缩放、标准化。
0-1缩放：(x-Min)/(Max-Min)
非常简单，但是容易受到异常值的影响。（举个栗子：本来属性值大部分处于0~ 15之间，突然有一个异常值为100，那么缩放之后大部分的属性值被缩放到0~ 0.15之间，而不是0~ 1之间。）
标准化：(x-均值)/方差
不容易受到异常值的影响。
所以本案例采用标准化方式：根据sklearn提供的standardScaler类，很方便的进行属性缩放。（在后文应用）

5、封装成流水线

将以上几个步骤封装起来，便于对任意数据集处理。
先把数值型数据的操作封装起来，在把数值型和文本/分类型属性一起封装。
首先，根据sklearn提供的Pipeline类，进行初步封装。

#安排数据转换的正确步骤
from sklearn.pipeline import Pipeline#通过一系列转换器/估算器定义步骤序列
from sklearn.preprocessing import StandardScaler
#定义转换器：
num_pipeline = Pipeline([
    ('imputer', SimpleImputer(strategy = "median")),  #转换器：缺失值替换成中位数
    ('attribs_adder', CombinedAttributesAdder()),  #自定义转换器：处理数据
    ('std_scaler', StandardScaler()),  #缩放器
])
housing_num_tr = num_pipeline.fit_transform(housing_num)#对所有数值列

housing_num_tr = pd.DataFrame(housing_num_tr) 
print(housing_num_tr.info(0))

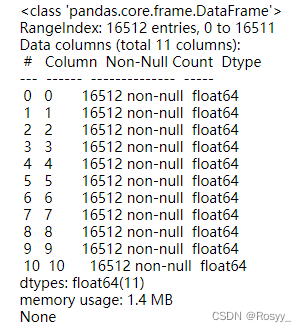
至此封装好了数值型数据的处理。
接下来，根据sklearn提供的ColumnTransformer类进行进一步的封装。

from sklearn.compose import ColumnTransformer
num_attribs = list(housing_num)
cat_attribs = ["ocean_proximity"]
#定义转换器：
full_pipeline = ColumnTransformer([ #创建个ColumnTransformer类对象
    ("num", num_pipeline, num_attribs),
    ("cat", OneHotEncoder(), cat_attribs),
])
housing_prepared = full_pipeline.fit_transform(housing) 

至此，将所有的数据清洗操作全部封装在了full_pipeline中。

以上（一）、（二）完成了所有对训练数据集的操作。

（三）、模型选择

1、线性模型

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)
housing_predictions = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels, housing_predictions) #计算rmse，[y, f(x)]
lin_rmse = np.sqrt(lin_mse)
print(lin_rmse)

结果坏掉了，欠拟合：1.选择更大的模型2.选择更好的特征3.减少对模型的限制，如去掉正则化。
线性模型-交叉验证：

from sklearn.model_selection import cross_val_score
#线性模型的评分：
lin_scores = cross_val_score(lin_reg, housing_prepared, housing_labels,scoring = "neg_mean_squared_error", cv = 10)
lin_rmse_scores = np.sqrt(-lin_scores)
print("LinearRegression")
display_scores(lin_rmse_scores)
#线性模型评分6万9

2、决策树

from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor()
tree_reg.fit(housing_prepared, housing_labels)#1.fit
housing_predictions = tree_reg.predict(housing_prepared)#2.predict
tree_mse = mean_squared_error(housing_labels, housing_predictions)
tree_rmse = np.sqrt(tree_mse)
print(tree_rmse)

训练集上结果太好，猜测严重过拟合：1.选择简单模型2.收集更多训练数据3.减少训练噪声。
决策树-交叉验证：

from sklearn.model_selection import cross_val_score
#决策树先来交叉验证，评分
scores = cross_val_score(tree_reg, housing_prepared, housing_labels, scoring = "neg_mean_squared_error", cv = 10)
tree_rmse_scores = np.sqrt(-scores)#效用函数，越大越好

def display_scores(scores):#结果每次运行均会在某区间变动
    print("Scores:", scores)
    print("Mean:", scores.mean())
    print("Standard deviation:", scores.std())

print("DecisionTreeRegressor:")
display_scores(tree_rmse_scores)

发现决策树如果采用交叉验证的话，评分7万，说明在整个测试集上确实过拟合。

3、随机森林

from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor()#0.类
forest_reg.fit(housing_prepared, housing_labels)#1.fit
housing_predictions = forest_reg.predict(housing_prepared)#2.predict
forest_mse = mean_squared_error(housing_labels, housing_predictions)#3.rmse
forest_rmse = np.sqrt(forest_mse)
print(forest_rmse)

随机森林-交叉验证：

from sklearn.model_selection import cross_val_score

#随机森林的评分
forest_scores = cross_val_score(forest_reg, housing_prepared, housing_labels, scoring = "neg_mean_squared_error", cv =10)
forest_rmse_scores = np.sqrt(-forest_scores)
print("RandomForestRegressor:")
display_scores(forest_rmse_scores)

随机森林单看rmse的值，似乎很有戏，但依旧比交叉验证的评分低很多，意味着模型也是过拟合。
不论如何，相比于前两种模型，表现稍好，所以接下来将随机森林应用于案例。

（四）、模型微调

常用的模型微调方法就是网格搜索。
根据sklearn提供的GridSearchCV类，告知其超参数有哪些、需要尝试的参数值，他就会根据交叉验证来评估所有超参数的可能组合。

from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestRegressor
param_grid = [
    {'n_estimators': [3, 10, 30], 'max_features': [2, 4, 6, 8]},
    {'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [2, 3, 4]},
]
forest_reg = RandomForestRegressor()
grid_search = GridSearchCV(forest_reg, param_grid, cv = 5, scoring = 'neg_mean_squared_error', return_train_score = True)

grid_search.fit(housing_prepared, housing_labels)

grid_search.best_params_

得到最终的最优的一组超参数，使用的数据不同，该结果也会有不同。

（五）、预测结果

将上面选出的最好的超参数对应的模型应用于测试数据。
首先还是现将测试数据及进行标签分离，然后应用前面封装好的数据清洗流水线full_pipeline进行处理，接下来便可用于房价预测：

final_model = grid_search.best_estimator_
X_test = strat_test_set.drop("median_house_value", axis = 1)
y_test = strat_test_set["median_house_value"].copy()

X_test_prepared = full_pipeline.transform(X_test)
final_predictions = final_model.predict(X_test_prepared)

final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse)
print(final_rmse)

得到的测试集上的评分往往会略逊于之前交叉验证的表现结果。虽然这里的结果并非如此，但也不要再调整超参数了，因为即使改变在泛化到新数据时也没有什么用了。

至此，整个案例的流程就走完了。