动手深度学习PyTorch（十二）word2vec

独热编码

独热编码即 One-Hot 编码，又称一位有效编码，其方法是使用N位状态寄存器来对N个状态进行编码，每个状态都有它独立的寄存器位，并且在任意时候，其中只有一位有效。举个例子，假设我们有四个样本（行），每个样本有三个特征（列），如图：

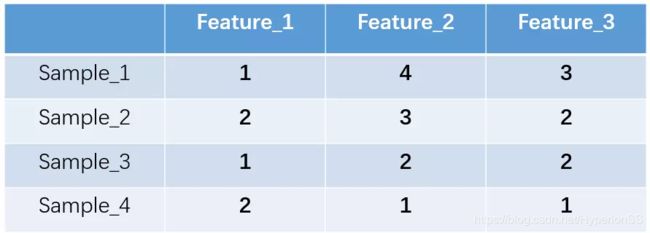
我们的feature_1有两种可能的取值，比如是男/女，这里男用1表示，女用2表示。feature_2 和feature_3各有4种取值（状态）。one-hot编码就是保证每个样本中的单个特征只有1位处于状态1，其他的都是0。上述状态用one-hot编码如下图所示：

考虑一下的三个特征：
[“male”, “female”]
[“from Europe”, “from US”, “from Asia”]
[“uses Firefox”, “uses Chrome”, “uses Safari”, “uses Internet Explorer”]

将它换成独热编码后，应该是：
feature1=[01,10]
feature2=[001,010,100]
feature3=[0001,0010,0100,1000]

优缺点分析

优点：一是解决了分类器不好处理离散数据的问题，二是在一定程度上也起到了扩充特征的作用。

缺点：在文本特征表示上有些缺点就非常突出了。首先，它是一个词袋模型，不考虑词与词之间的顺序（文本中词的顺序信息也是很重要的）；其次，它假设词与词相互独立（在大多数情况下，词与词是相互影响的）；最后，它得到的特征是离散稀疏的。

为什么得到的特征是离散稀疏的？

上面举例比较简单，但现实情况可能不太一样。比如如果将世界所有城市名称作为语料库的话，那这个向量会过于稀疏，并且会造成维度灾难。

杭州 [0,0,0,0,0,0,0,1,0,……，0,0,0,0,0,0,0]
上海 [0,0,0,0,1,0,0,0,0,……，0,0,0,0,0,0,0]
宁波 [0,0,0,1,0,0,0,0,0,……，0,0,0,0,0,0,0]
北京 [0,0,0,0,0,0,0,0,0,……，1,0,0,0,0,0,0]

在语料库中，杭州、上海、宁波、北京各对应一个向量，向量中只有一个值为1，其余都为0。

能不能把词向量的维度变小呢？

Dristributed representation可以解决One hot representation的问题，它的思路是通过训练，将每个词都映射到一个较短的词向量上来。所有的这些词向量就构成了向量空间，进而可以用普通的统计学的方法来研究词与词之间的关系。这个较短的词向量维度是多大呢？这个一般需要我们在训练时自己来指定。

比如下图我们将词汇表里的词用"Royalty",“Masculinity”, "Femininity"和"Age"4个维度来表示，King这个词对应的词向量可能是(0.99,0.99,0.05,0.7)(0.99,0.99,0.05,0.7)。当然在实际情况中，我们并不能对词向量的每个维度做一个很好的解释。

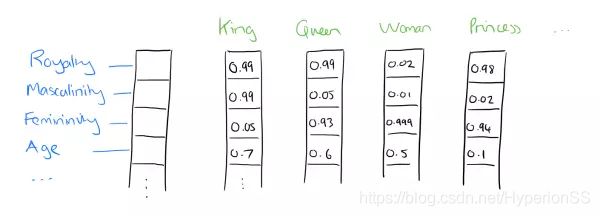
我们将king这个词从一个可能非常稀疏的向量坐在的空间，映射到现在这个四维向量所在的空间，必须满足以下性质：

（1）这个映射是单设（不懂的概念自行搜索）；
（2）映射之后的向量不会丢失之前的那种向量所含的信息。

这个过程称为word embedding（词嵌入），即将高维词向量嵌入到一个低维空间。顺便找了个图

经过我们一系列的降维神操作，有了用Dristributed representation表示的较短的词向量，我们就可以较容易的分析词之间的关系了，比如我们将词的维度降维到2维，有一个有趣的研究表明，用下图的词向量表示我们的词时，我们可以发现：

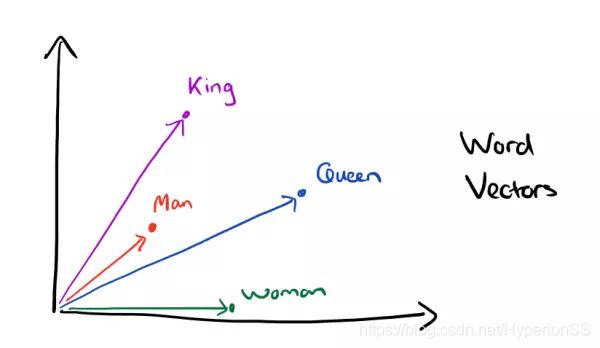
是不是好像发现了什么了不得的事情？

出现这种现象的原因是，我们得到最后的词向量的训练过程中引入了词的上下文。

词嵌入（word2vec）

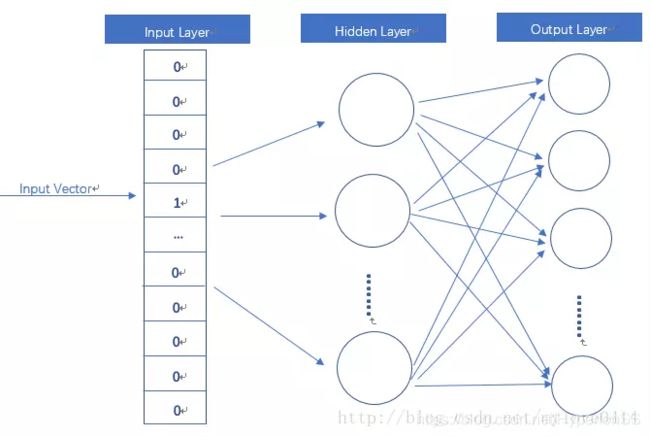
word2vec模型其实就是简单化的神经网络。

输入是One-Hot Vector，Hidden Layer没有激活函数，也就是线性的单元。Output Layer维度跟Input Layer的维度一样，用的是Softmax回归。当这个模型训练好以后，我们并不会用这个训练好的模型处理新的任务，我们真正需要的是这个模型通过训练数据所学得的参数，例如隐层的权重矩阵。

这个模型是如何定义数据的输入和输出呢？一般分为CBOW(Continuous Bag-of-Words 与Skip-Gram两种模型。CBOW模型的训练输入是某一个特征词的上下文相关的词对应的词向量，而输出就是这特定的一个词的词向量。　Skip-Gram模型和CBOW的思路是反着来的，即输入是特定的一个词的词向量，而输出是特定词对应的上下文词向量。CBOW对小型数据库比较合适，而Skip-Gram在大型语料中表现更好。

跳字模型（Skip-Gram）

跳字模型假设基于某个词来生成它在文本序列周围的词。举个例子，假设文本序列是“the”“man”“loves”“his”“son”。以“loves”作为中心词，设背景窗口大小为2。如图10.1所示，跳字模型所关心的是，给定中心词“loves”，生成与它距离不超过2个词的背景词“the”“man”“his”“son”的条件概率，即

$$P(\text{“the"},\text{“man"},\text{“his"},\text{“son"}\mid \text{“loves"}).$$

假设给定中心词的情况下，背景词的生成是相互独立的，那么上式可以改写成

$$P(\text{“the"}\mid \text{“loves"})\cdot P(\text{“man"}\mid \text{“loves"})\cdot P(\text{“his"}\mid \text{“loves"})\cdot P(\text{“son"}\mid \text{“loves"}).$$

在跳字模型中，每个词被表示成两个$d$维向量，用来计算条件概率。假设这个词在词典中索引为$i$，当它为中心词时向量表示为${\mathbf{v}}_i\in {\mathbb{R}}^d$，而为背景词时向量表示为${\mathbf{u}}_i\in {\mathbb{R}}^d$。设中心词$w_c$在词典中索引为$c$，背景词$w_o$在词典中索引为$o$，给定中心词生成背景词的条件概率可以通过对向量内积做softmax运算而得到：

$$P(w_o\mid w_c)=\frac{\text{exp}({\mathbf{u}}_o^{\top }{\mathbf{v}}_c)}{{\sum }_{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)},$$

其中词典索引集$\mathcal{V}=\{0,1,\dots ,|\mathcal{V}|-1\}$。假设给定一个长度为$T$的文本序列，设时间步$t$的词为$w^{(t)}$。假设给定中心词的情况下背景词的生成相互独立，当背景窗口大小为$m$时，跳字模型的似然函数即给定任一中心词生成所有背景词的概率

$$\prod _{t=1}^T\prod _{-m\le j\le m,j\ne 0}P(w^{(t+j)}\mid w^{(t)}),$$

这里小于1和大于$T$的时间步可以忽略。

训练跳字模型

跳字模型的参数是每个词所对应的中心词向量和背景词向量。训练中我们通过最大化似然函数来学习模型参数，即最大似然估计。这等价于最小化以下损失函数：

$$-\sum _{t=1}^T\sum _{-m\le j\le m,j\ne 0}\text{log}P(w^{(t+j)}\mid w^{(t)}).$$

如果使用随机梯度下降，那么在每一次迭代里我们随机采样一个较短的子序列来计算有关该子序列的损失，然后计算梯度来更新模型参数。梯度计算的关键是条件概率的对数有关中心词向量和背景词向量的梯度。根据定义，首先看到

$$\log P(w_o\mid w_c)={\mathbf{u}}_o^{\top }{\mathbf{v}}_c-\log \left(\sum _{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)\right)$$

通过微分，我们可以得到上式中${\mathbf{v}}_c$的梯度

$$\begin{array}{rl}\frac{\partial \text{log}P(w_o\mid w_c)}{\partial {\mathbf{v}}_c}& ={\mathbf{u}}_o-\frac{{\sum }_{j\in \mathcal{V}}\exp ({\mathbf{u}}_j^{\top }{\mathbf{v}}_c){\mathbf{u}}_j}{{\sum }_{i\in \mathcal{V}}\exp ({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)}\\ & ={\mathbf{u}}_o-\sum _{j\in \mathcal{V}}\left(\frac{\text{exp}({\mathbf{u}}_j^{\top }{\mathbf{v}}_c)}{{\sum }_{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)}\right){\mathbf{u}}_j\\ & ={\mathbf{u}}_o-\sum _{j\in \mathcal{V}}P(w_j\mid w_c){\mathbf{u}}_j.\end{array}$$

它的计算需要词典中所有词以$w_c$为中心词的条件概率。有关其他词向量的梯度同理可得。

训练结束后，对于词典中的任一索引为$i$的词，我们均得到该词作为中心词和背景词的两组词向量${\mathbf{v}}_i$和${\mathbf{u}}_i$。在自然语言处理应用中，一般使用跳字模型的中心词向量作为词的表征向量。

10.1.3 连续词袋模型

连续词袋模型与跳字模型类似。与跳字模型最大的不同在于，连续词袋模型假设基于某中心词在文本序列前后的背景词来生成该中心词。在同样的文本序列“the”“man”“loves”“his”“son”里，以“loves”作为中心词，且背景窗口大小为2时，连续词袋模型关心的是，给定背景词“the”“man”“his”“son”生成中心词“loves”的条件概率（如图10.2所示），也就是

$$P(\text{“loves"}\mid \text{“the"},\text{“man"},\text{“his"},\text{“son"}).$$

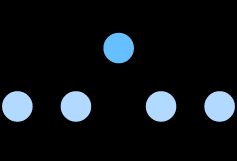
因为连续词袋模型的背景词有多个，我们将这些背景词向量取平均，然后使用和跳字模型一样的方法来计算条件概率。设${\mathbf{v}}_{\mathbf{i}}\in {\mathbb{R}}^d$和${\mathbf{u}}_{\mathbf{i}}\in {\mathbb{R}}^d$分别表示词典中索引为$i$的词作为背景词和中心词的向量（注意符号的含义与跳字模型中的相反）。设中心词$w_c$在词典中索引为$c$，背景词$w_{o_1},\dots ,w_{o_{2m}}$在词典中索引为$o_1,\dots ,o_{2m}$，那么给定背景词生成中心词的条件概率

$$P(w_c\mid w_{o_1},\dots ,w_{o_{2m}})=\frac{\text{exp}\left(\frac{1}{2m}{\mathbf{u}}_c^{\top }({\mathbf{v}}_{o_1}+\dots +{\mathbf{v}}_{o_{2m}})\right)}{{\sum }_{i\in \mathcal{V}}\text{exp}\left(\frac{1}{2m}{\mathbf{u}}_i^{\top }({\mathbf{v}}_{o_1}+\dots +{\mathbf{v}}_{o_{2m}})\right)}.$$

为了让符号更加简单，我们记${\mathcal{W}}_o=\{w_{o_1},\dots ,w_{o_{2m}}\}$，且${\bar{\mathbf{v}}}_o=\left({\mathbf{v}}_{o_1}+\dots +{\mathbf{v}}_{o_{2m}}\right)/(2m)$，那么上式可以简写成

$$P(w_c\mid {\mathcal{W}}_o)=\frac{\exp \left({\mathbf{u}}_c^{\top }{\bar{\mathbf{v}}}_o\right)}{{\sum }_{i\in \mathcal{V}}\exp \left({\mathbf{u}}_i^{\top }{\bar{\mathbf{v}}}_o\right)}.$$

给定一个长度为$T$的文本序列，设时间步$t$的词为$w^{(t)}$，背景窗口大小为$m$。连续词袋模型的似然函数是由背景词生成任一中心词的概率

$$\prod _{t=1}^{T}P(w^{(t)}\mid w^{(t-m)},\dots ,w^{(t-1)},w^{(t+1)},\dots ,w^{(t+m)}).$$

10.1.3.1 训练连续词袋模型

训练连续词袋模型同训练跳字模型基本一致。连续词袋模型的最大似然估计等价于最小化损失函数

$$-\sum _{t=1}^T\text{log}P(w^{(t)}\mid w^{(t-m)},\dots ,w^{(t-1)},w^{(t+1)},\dots ,w^{(t+m)}).$$

注意到

$$\log P(w_c\mid {\mathcal{W}}_o)={\mathbf{u}}_c^{\top }{\bar{\mathbf{v}}}_o-\log \left(\sum _{i\in \mathcal{V}}\exp \left({\mathbf{u}}_i^{\top }{\bar{\mathbf{v}}}_o\right)\right).$$

通过微分，我们可以计算出上式中条件概率的对数有关任一背景词向量${\mathbf{v}}_{o_i}$（$i=1,\dots ,2m$）的梯度

$$\frac{\partial \log P(w_c\mid {\mathcal{W}}_o)}{\partial {\mathbf{v}}_{o_i}}=\frac{1}{2m}\left({\mathbf{u}}_c-\sum _{j\in \mathcal{V}}\frac{\exp ({\mathbf{u}}_j^{\top }{\bar{\mathbf{v}}}_o){\mathbf{u}}_j}{{\sum }_{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\bar{\mathbf{v}}}_o)}\right)=\frac{1}{2m}\left({\mathbf{u}}_c-\sum _{j\in \mathcal{V}}P(w_j\mid {\mathcal{W}}_o){\mathbf{u}}_j\right).$$

有关其他词向量的梯度同理可得。同跳字模型不一样的一点在于，我们一般使用连续词袋模型的背景词向量作为词的表征向量。

参考资料

https://www.zhihu.com/question/53354714
https://www.zhihu.com/question/32275069/answer/80188672
https://www.cnblogs.com/lianyingteng/p/7755545.html
http://blog.clzg.cn/blog-1579109-884831.html
https://www.cnblogs.com/haobang008/p/5911466.html
https://www.zhihu.com/question/44832436/answer/266068967
https://baijiahao.baidu.com/s?id=1589564139527612155&wfr=spider&for=pc
https://www.jianshu.com/p/cede3ae146bb
https://www.jianshu.com/p/f58c08ae44a6
https://blog.csdn.net/mylove0414/article/details/61616617
https://www.cnblogs.com/pinard/p/7160330.html
https://www.leiphone.com/news/201706/PamWKpfRFEI42McI.html
https://www.leiphone.com/news/201706/eV8j3Nu8SMqGBnQB.html
https://www.zhihu.com/question/44832436/answer/266068967