Bishop 模式识别与机器学习读书笔记_ch2.2 连续性概率分布
ch2.2 连续型概率分布
1. 高斯分布
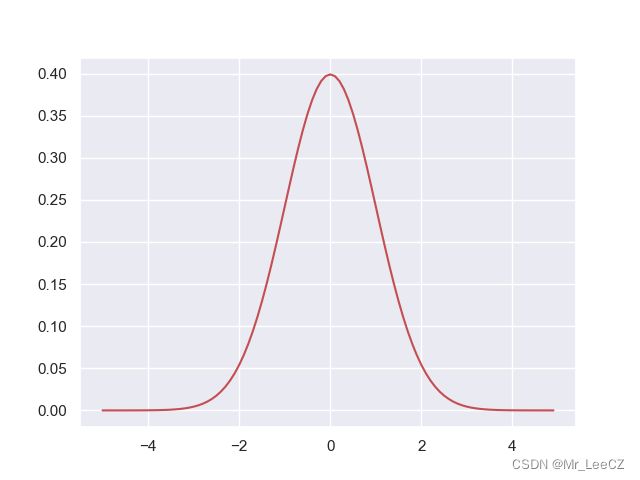
⾼斯分布,也被称为正态分布,⼴泛应⽤于连续型随机变量分布的模型中。对于⼀元变量 x x x 的情形,⾼斯分布可以写成下⾯的形式
KaTeX parse error: Undefined control sequence: \notag at position 104: …\sigma^2}\Big\}\̲n̲o̲t̲a̲g̲ ̲
此处, μ \mu μ 表示均值, σ 2 \sigma^2 σ2 表示方差。
import math
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style="darkgrid")
mu = 0
sigma = 1
x = np.arange(-5, 5, 0.1)
y = np.exp((x-mu)**2/(-2*sigma**2))/math.sqrt(2*math.pi*sigma**2)
plt.plot(x, y, 'r-')
plt.show()
对于 D D D-维向量 x \mathbf{x} x,高斯分布表示为
KaTeX parse error: Undefined control sequence: \notag at position 176: …hbf{\mu})\Big\}\̲n̲o̲t̲a̲g̲ ̲
此处, μ \mathbf{\mu} μ 表示 D D D 维均值向量, Σ \Sigma Σ 为 D × D D\times D D×D 维的协方差矩阵, ∣ ⋅ ∣ \vert\cdot\vert ∣⋅∣ 表示矩阵的行列式。
#!/usr/bin/python
# -*- coding:utf-8 -*-
import numpy as np
from scipy import stats
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
if __name__ == '__main__':
x1, x2 = np.mgrid[-5:5:51j, -5:5:51j]
x = np.stack((x1, x2), axis=2)
print('x1 = \n', x1)
print('x2 = \n', x2)
print('x = \n', x)
mpl.rcParams['axes.unicode_minus'] = False
mpl.rcParams['font.sans-serif'] = 'SimHei'
plt.figure(figsize=(9, 8), facecolor='w')
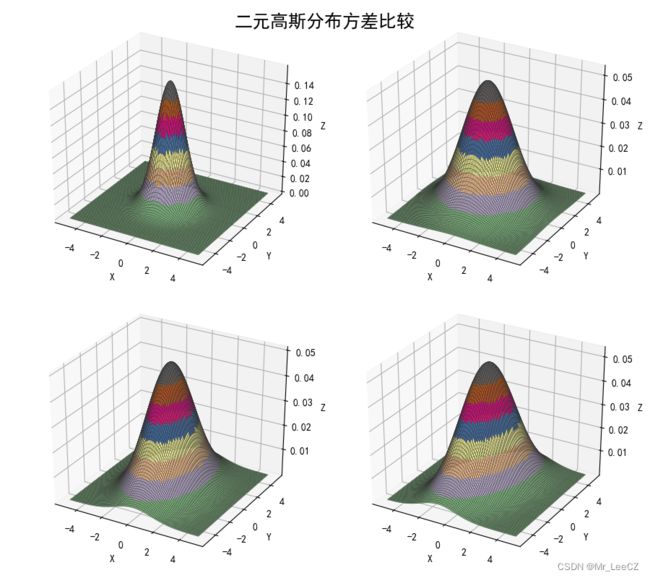
sigma = (np.identity(2), np.diag((3,3)), np.diag((2,5)), np.array(((2,1), (1,5))))
for i in np.arange(4):
ax = plt.subplot(2, 2, i+1, projection='3d')
norm = stats.multivariate_normal((0, 0), sigma[i])
y = norm.pdf(x)
ax.plot_surface(x1, x2, y, cmap=cm.Accent, rstride=1, cstride=1, alpha=0.9, lw=0.3, edgecolor='#303030')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.suptitle('二元高斯分布方差比较', fontsize=18)
plt.tight_layout(1.5)
plt.show()
高斯分布会在许多不同的问题中产生,可以从多个不同的角度来理解。例如,我们可以看到,对于一个一元实值向量,使熵取得最大值的是高斯分布。这个性质对于多元高斯也成立。
当我们考虑多个随机变量之和的时候,也会产生高斯分布。拉普拉斯提出的中心极限定理(central limit theorem)告诉我们,对于某些温和的情况,⼀组随机变量之和(当然也是随机变量)的概率分布随着和式中项的数量的增加而逐渐趋向高斯分布(Walker,1969)。考虑 N N N 个变量(特征或列) { x i ∈ R ∣ i = 1 , ⋯ , N } \{x_i\in R\vert i=1,\cdots,N\} {xi∈R∣i=1,⋯,N},每⼀个都是区间 [ 0 , 1 ] [0,1] [0,1] 上的均匀分布,然后考虑均值(列均值) ( x 1 + ⋯ + x N ) / N (x_1+\cdots+x_N)/N (x1+⋯+xN)/N 的分布。对于大的N,这个分布趋向于高斯分布,如图所示(样本点个数设定为10万)。
import matplotlib.pyplot as plt
from scipy.stats import uniform
plt.figure(figsize=(10, 5))
plt.subplot(1, 3, 1)
plt.xlim(0, 1)
plt.ylim(0, 5)
plt.annotate("N=1", (0.1, 4.5))
print(uniform.rvs(5)) # 与下一行相比,加不加参数“size=”,有天壤之别
plt.hist(uniform.rvs(size=100000), bins=20, density=True)
plt.subplot(1, 3, 2)
plt.xlim(0, 1)
plt.ylim(0, 5)
plt.annotate("N=2", (0.1, 4.5))
plt.hist(0.5 * (uniform.rvs(size=100000) + uniform.rvs(size=100000)), bins=20, density=True)
plt.subplot(1, 3, 3)
plt.xlim(0, 1)
plt.ylim(0, 5)
sample = 0
for _ in range(10):
sample = sample + uniform.rvs(size=100000)
plt.annotate("N=10", (0.1, 4.5))
plt.hist(sample * 0.1, bins=20, density=True)
plt.show()
在实际应⽤中,随着 N N N 的增加,分布会很迅速收敛为高斯分布。这个结论导致的⼀个结果是,⼆项分布(⼆元随机变量 x x x 在 N N N 次观测中出现次数 m m m 的分布)将会在 N → ∞ N\to\infty N→∞ 时趋向于高斯分布。高斯分布有许多重要的分析性质,且需要对各种矩阵性质比较熟悉。我们强烈鼓励读者能够使用这里介绍的技术熟练操作高斯分布,因为这对于理解后续章节中出现的更加复杂的模型是非常有帮助的。
2. 高斯分布的几何结构
高斯函数中自变量 x x x 的函数依赖关系是通过指数部分的二次型实现的,
Δ 2 = ( x − μ ) T Σ − 1 ( x − μ ) \Delta^2=(\boldsymbol{x}-\boldsymbol{\mu})^T\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu}) Δ2=(x−μ)TΣ−1(x−μ)
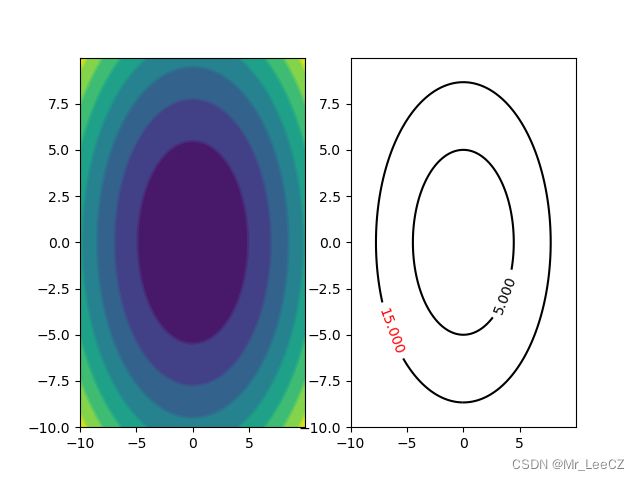
这个量我们称为 μ \boldsymbol{\mu} μ 到 x \boldsymbol{x} x 的 Mahalanobis 距离,而当 Σ = I \Sigma=I Σ=I 时,该量称为 μ \boldsymbol{\mu} μ 到 x \boldsymbol{x} x 的欧氏距离。该二次型如果是常数 Δ 2 = c o n s t \Delta^2=const Δ2=const 可以描述为等高线,如下图所示
#导入模块
import numpy as np
import matplotlib.pyplot as plt
#建立步长为0.01,即每隔0.01取一个点
step = 0.01
x = np.arange(-10,10,step)
y = np.arange(-10,10,step)
#也可以用x = np.linspace(-10,10,100)表示从-10到10,分100份
#将原始数据变成网格数据形式
X,Y = np.meshgrid(x,y)
#写入函数,z是大写
Z = X**2/4+Y**2/5
#设置打开画布大小,长10,宽6
#plt.figure(figsize=(10,6))
plt.subplot(1,2,1)
#填充颜色,f即filled
plt.contourf(X,Y,Z)
#画等高线
plt.contour(X,Y,Z)
plt.subplot(1,2,2)
contour = plt.contour(X,Y,Z,[5,15],colors='k')
#等高线上标明z(即高度)的值,字体大小是10,颜色分别是黑色和红色
plt.clabel(contour,fontsize=10,colors=('k','r'))
plt.show()
注释: 由于此程序只考虑了高斯函数指数部分的相反数,所以等高线越往外值越大,如果考虑高斯函数的整体,则等高线越往里越大。
3. 高斯分布的性质
高斯函数本质上是对距离函数的一个非线性变换,主要体现在高斯函数指数部分的 x \mathbf{x} x 到 μ \mu μ 距离的二次型上
KaTeX parse error: Undefined control sequence: \notag at position 75: …-\mathbf{\mu}) \̲n̲o̲t̲a̲g̲ ̲
其中, Δ \Delta Δ 称为 x \mathbf{x} x 到 中心点 μ \mathbf{\mu} μ 的 Mahalanobis 距离,当 Σ = I \Sigma=\mathbf{I} Σ=I时该距离退化成欧氏距离。由于矩阵 Σ \Sigma Σ 是一个实对称矩阵,因此,可以实现矩阵的对角化,即存在一组线性无关的基底 [ u 1 , u 2 , ⋯ , u D ] [\mathbf{u}_1, \mathbf{u}_2, \cdots,\mathbf{u}_D] [u1,u2,⋯,uD] 使得
KaTeX parse error: Undefined control sequence: \notag at position 260: …dots,\lambda_D)\̲n̲o̲t̲a̲g̲ ̲
或 U Σ U T = Diag ( λ 1 , λ 2 , ⋯ , λ D ) \mathbf{U}\Sigma\mathbf{U}^T=\text{Diag}(\lambda_1,\lambda_2,\cdots,\lambda_D) UΣUT=Diag(λ1,λ2,⋯,λD)
即
KaTeX parse error: Undefined control sequence: \notag at position 69: …i=1,2,\cdots,D \̲n̲o̲t̲a̲g̲ ̲
其中,基是标准正交基
KaTeX parse error: Undefined control sequence: \notag at position 68: …\mathbf{u}_j=0 \̲n̲o̲t̲a̲g̲ ̲
或 U U T = I \mathbf{U}\mathbf{U}^T=\mathbf{I} UUT=I
又因为
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \Sigma&=\mathb…
可知
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \Sigma^{-1}&=\…
将(2)带入 (1)得
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \Delta^2&=(\bo…
或者
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \Delta^2&=(\bo…
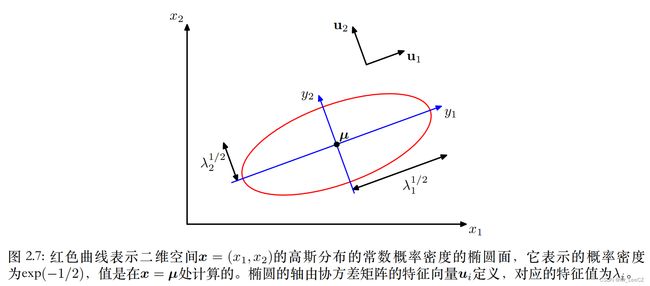
由公式(3)可知, Δ 2 = ∑ i D 1 λ i y i 2 = c o n s t \Delta^2=\sum_i^D\frac{1}{\lambda_i}y_i^2=const Δ2=∑iDλi1yi2=const,(椭圆的轴)此时,高斯密度函数也是常数,即可表示出等高线。通过坐标变换 y = U ( x − μ ) \boldsymbol{y}=\boldsymbol{U}(\boldsymbol{x}-\boldsymbol{\mu}) y=U(x−μ) 将椭圆的主轴做了旋转,坐标轴由 x x x 轴转变为 y y y 轴,如图所示。矩阵 U \boldsymbol{U} U 是把原始坐标轴旋转到投影长度最大的的坐标轴,即通过特征值分解获得的特征向量。
对于高斯分布,有必要要求协方差矩阵的所有特征值 λ i \lambda_i λi 严格大于零,否则分布将不能被正确地归⼀化。⼀个特征值严格大于零的矩阵被称为正定(positive definite)矩阵。在第12章,我们会遇到⼀个或者多个特征值为零的高斯分布,那种情况下分布是奇异的,被限制在了⼀个低维的子空间中。如果所有的特征值都是非负的,那么这个矩阵被称为半正定(positive semidefine)矩阵。
注解: 数据如果在某个或者几个坐标轴的无投影的话,则可以用少数的坐标轴进行表示,即子空间。
现在考虑在由 y i y_i yi 定义的新坐标系下高斯分布的形式。从 x \boldsymbol{x} x 坐标系到 y \boldsymbol{y} y 坐标系,我们有⼀个Jacobian矩阵 J \boldsymbol{J} J,它的元素可通过一下推导进行表示。
由公式 y = U ( x − μ ) \boldsymbol{y}=\boldsymbol{U}(\boldsymbol{x}-\boldsymbol{\mu}) y=U(x−μ) 可得 x = U T y + μ \boldsymbol{x}=\boldsymbol{U}^T\boldsymbol{y}+\boldsymbol{\mu} x=UTy+μ,则
KaTeX parse error: Undefined control sequence: \notag at position 93: …symbol{U}_{ji} \̲n̲o̲t̲a̲g̲ ̲
或者 J = U T \boldsymbol{J}=\boldsymbol{U}^T J=UT
其中, U j i \boldsymbol{U}_{ji} Uji 是矩阵 U T \boldsymbol{U}^T UT 的元素。由于 U \boldsymbol{U} U 矩阵的正交性,雅可比矩阵的行列式可表示为
KaTeX parse error: Undefined control sequence: \notag at position 181: …ymbol{I}\vert=1\̲n̲o̲t̲a̲g̲ ̲
由 Σ = U T ⋅ Diag ( λ 1 , λ 2 , ⋯ , λ D ) ⋅ U \Sigma=\mathbf{U}^T\cdot\text{Diag}(\lambda_1,\lambda_2,\cdots,\lambda_D)\cdot\mathbf{U} Σ=UT⋅Diag(λ1,λ2,⋯,λD)⋅U 可知,
∣ Σ ∣ 1 / 2 = ∏ j = 1 D λ j 1 / 2 (5) \vert\Sigma\vert^{1/2}=\prod_{j=1}^D\lambda_j^{1/2}\tag{5} ∣Σ∣1/2=j=1∏Dλj1/2(5)
将公式(2)和(5)带入高斯概率密度函数的
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ p(\boldsymbol{…
在新的坐标系 y \boldsymbol{y} y 下,概率密度函数 p ( y ) p(\boldsymbol{y}) p(y) 仍然是不需要归一化的,因为
KaTeX parse error: Undefined control sequence: \notag at position 136: …j}\Big\}dy_j=1 \̲n̲o̲t̲a̲g̲ ̲
3.1 高斯分布的期望
高斯概率密度函数 p ( x ) = 1 ( 2 π ) D / 2 ∣ Σ ∣ 1 / 2 exp { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } p(\boldsymbol{x})=\frac{1}{(2\pi)^{D/2}\vert\Sigma\vert^{1/2}}\exp\Big\{−\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\Big\} p(x)=(2π)D/2∣Σ∣1/21exp{−21(x−μ)TΣ−1(x−μ)} 有两个参数, μ \boldsymbol{\mu} μ 和 Σ \Sigma Σ。下面分别计算高斯概率密度函数关于 x \boldsymbol{x} x 的期望和方差。
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲\mathbb{E}[\bol…
所示, μ \boldsymbol{\mu} μ 称为高斯分布的均值。
3.2 高斯分布的方差
要求多维高斯分布的方差,首先我们需要求 E [ x ⋅ x T ] \mathbb{E}[\boldsymbol{x}\cdot\boldsymbol{x}^T] E[x⋅xT],
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \mathbb{E}[\bo…
由公式(4) y = U ( x − μ ) \boldsymbol{y}=\mathbf{U}(\boldsymbol{x}-\boldsymbol{\mu}) y=U(x−μ) 及上式代换 z = x − μ \boldsymbol{z}=\boldsymbol{x}-\boldsymbol{\mu} z=x−μ 可得 z = ∑ j = 1 D y j u j \boldsymbol{z}=\sum_{j=1}^Dy_j\boldsymbol{u}_j z=∑j=1Dyjuj,则上式可继续表示为
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \mathbb{E}[\bo…
则
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ cov[\boldsymbo…
因为高斯分布的参数矩阵 Σ \Sigma Σ 控制着 x x x 的方差,称为协方差矩阵。
3.2 高斯分布的弊端
高斯分布的参数包括均值向量 μ \boldsymbol{\mu} μ 和 协方差矩阵 Σ \Sigma Σ ,这种各向异性高斯分布虽然表达能力强,但是包含参数个数多,为 D + D ( D − 1 ) / 2 = D ( D + 1 ) / 2 D+D(D-1)/2=D(D+1)/2 D+D(D−1)/2=D(D+1)/2个;为了减少参数个数,可降低高斯密度函数的表达能力,可设定 Σ = σ 2 I \Sigma=\sigma^2 I Σ=σ2I, 变成各向同性高斯分布,此时的参数个数为 D + 1 D+1 D+1 个。
单高斯密度函数最大的问题是不能表达多高斯分布,需要借助更深层的学习,引入潜在变量和多模态高斯,主要应用于马尔可夫随机场和线性动态系统,一个有效的计算框架是概率图模型。
4. 高斯的极大似然
观测数据 X = ( x 1 , x 2 , ⋯ , x n ) T X=(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n)^T X=(x1,x2,⋯,xn)T 中每个样本(行向量)均独立采样于多维高斯分布
KaTeX parse error: Undefined control sequence: \notag at position 193: …bol{\mu})\Big\}\̲n̲o̲t̲a̲g̲ ̲
则
KaTeX parse error: Undefined control sequence: \notag at position 195: …bol{\mu})\Big\}\̲n̲o̲t̲a̲g̲ ̲
即
ln p ( X ∣ μ , Σ ) = N D 2 ln ( 2 π ) − N 2 ln ∣ Σ ∣ − 1 2 ∑ n = 1 N ( x n − μ ) T Σ − 1 ( x n − μ ) (6) \ln p(X\vert\boldsymbol{\mu},\Sigma)=\frac{ND}{2}\ln(2\pi)-\frac{N}{2}\ln\vert\Sigma\vert−\frac{1}{2}\sum_{n=1}^N(\mathbf{x}_n-\boldsymbol{\mu})^T\Sigma^{-1}(\mathbf{x}_n-\boldsymbol{\mu}) \tag{6} lnp(X∣μ,Σ)=2NDln(2π)−2Nln∣Σ∣−21n=1∑N(xn−μ)TΣ−1(xn−μ)(6)
经过简单的整理,发现(6)只与两个量有关,分别为 ∑ n = 1 N x n \sum_{n=1}^N\mathbf{x}_n ∑n=1Nxn 和 ∑ n = 1 N x n x n T \sum_{n=1}^N\mathbf{x}_n\mathbf{x}_n^T ∑n=1NxnxnT 有关,称为高斯分布的充分统计量。
通过极大似然的方式可以求出参数 μ \boldsymbol{\mu} μ,
KaTeX parse error: Undefined control sequence: \notag at position 137: …symbol{\mu})=0 \̲n̲o̲t̲a̲g̲ ̲
即参数 μ \boldsymbol{\mu} μ 的极大似然解为
KaTeX parse error: Undefined control sequence: \notag at position 60: …^N\mathbf{x}_n \̲n̲o̲t̲a̲g̲ ̲
为观测值的均值。
接下来对 log 似然函数关于参数 Σ \Sigma Σ 求导数
KaTeX parse error: Undefined control sequence: \notag at position 247: …{\mu})\Bigg\}=0\̲n̲o̲t̲a̲g̲ ̲
得
KaTeX parse error: Undefined control sequence: \notag at position 124: …ol{\mu}_{ML})^T\̲n̲o̲t̲a̲g̲ ̲
这是一个有偏估计,因为
KaTeX parse error: Undefined control sequence: \notag at position 52: …boldsymbol{\mu}\̲n̲o̲t̲a̲g̲ ̲
KaTeX parse error: Undefined control sequence: \notag at position 71: …dsymbol{\Sigma}\̲n̲o̲t̲a̲g̲ ̲
为了得到无偏估计,我们需要做如下调整
KaTeX parse error: Undefined control sequence: \notag at position 134: …l{\mu}_{ML})^T \̲n̲o̲t̲a̲g̲ ̲
5. 高斯的贝叶斯推断
**问题:**高斯分布关于参数 μ \mu μ 和 Σ \Sigma Σ 的极大似然估计是一种点估计方法,过分地依赖观测数据,估计结果与总体分布难免有偏颇。
策略: 通过引入先验的方式开发贝叶斯方法,即引入超参数,由先验估计后验。
我们以简单的单变量高斯为例,假设总体分布的方差 σ 2 \sigma^2 σ2 已知,通过 N N N 个采样 x = { x 1 , x 2 , ⋯ , x n } \mathbf{x}=\{x_1,x_2,\cdots,x_n\} x={x1,x2,⋯,xn} 推断总体的均值 μ \mu μ. 关于参数 μ \mu μ 的似然函数表示为
KaTeX parse error: Undefined control sequence: \notag at position 141: …_i-\mu)^2\Big\}\̲n̲o̲t̲a̲g̲ ̲
**注意:**似然函数并未归一化,也不是一个概率密度函数。
由于似然函数是关于参数 μ \mu μ 的指数形式,可设定先验分布 p ( μ ) p(\mu) p(μ) 为高斯分布,后验分布也将是高斯分布,使得似然与后验分布具有相同的指数形式。因此,先验分布设定如下
KaTeX parse error: Undefined control sequence: \notag at position 130: …-\mu_0)^2\Big\}\̲n̲o̲t̲a̲g̲ ̲
则后验分布表示为
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \ln p(\mu\vert…
所以,后验分布为 p ( μ ∣ x ) = N ( μ ∣ μ ~ , σ ~ ) p(\mu\vert\mathbf{x})=\mathcal{N}(\mu\vert\widetilde{\mu},\widetilde{\sigma}) p(μ∣x)=N(μ∣μ ,σ ) ,其中,
μ ~ = N σ 0 2 ⋅ μ M L + σ 2 μ 0 N σ 0 2 + σ 2 = σ 2 N σ 0 2 + σ 2 μ 0 + N σ 0 2 N σ 0 2 + σ 2 μ M L (7) \widetilde{\mu}=\frac{N\sigma_0^2\cdot\mu_{ML}+\sigma^2\mu_0}{N\sigma_0^2+\sigma^2}=\frac{\sigma^2}{N\sigma_0^2+\sigma^2}\mu_0+\frac{N\sigma_0^2}{N\sigma_0^2+\sigma^2}\mu_{ML}\tag{7} μ =Nσ02+σ2Nσ02⋅μML+σ2μ0=Nσ02+σ2σ2μ0+Nσ02+σ2Nσ02μML(7)
1 σ 2 ~ = N σ 2 + 1 σ 0 2 (8) \frac{1}{\widetilde{\sigma^2}}=\frac{N}{\sigma^2}+\frac{1}{\sigma_0^2}\tag{8} σ2 1=σ2N+σ021(8)
由公式(7)可知,后验均值是先验均值和极大似然均值的折中。
- N = 0 N=0 N=0 时,强烈依赖于先验,后验均值等于先验均值
- N → ∞ N\to\infty N→∞ 时,强烈依赖于似然,后验均值等于似然均值
相似地,由公式(8)可知,后验的精度会随着 N N N 的增大而稳步增加
- N = 0 N=0 N=0 时,强烈依赖于先验,后验精度等于先验精度
- N → ∞ N\to\infty N→∞ 时,后验方差接近于 0 0 0 ,分布在极大似然均值附近变得陡峭
**注意:**对于固定的 N N N ,当 σ 0 2 → ∞ \sigma_0^2\to\infty σ02→∞ 时,后验均值会退化成极大似然均值;后验方差 σ 2 ~ = σ 2 / N \widetilde{\sigma^2}=\sigma^2/N σ2 =σ2/N,效果如下图所示。
1 σ 2 ~ = N σ 2 + 1 σ 0 2 (8) \frac{1}{\widetilde{\sigma^2}}=\frac{N}{\sigma^2}+\frac{1}{\sigma_0^2}\tag{8} σ2 1=σ2N+σ021(8)
由公式(7)可知,后验均值是先验均值和极大似然均值的折中。
- N = 0 N=0 N=0 时,强烈依赖于先验,后验均值等于先验均值
- N → ∞ N\to\infty N→∞ 时,强烈依赖于似然,后验均值等于似然均值
相似地,由公式(8)可知,后验的精度会随着 N N N 的增大而稳步增加
- N = 0 N=0 N=0 时,强烈依赖于先验,后验精度等于先验精度
- N → ∞ N\to\infty N→∞ 时,后验方差接近于 0 0 0 ,分布在极大似然均值附近变得陡峭
**注意:**对于固定的 N N N ,当 σ 0 2 → ∞ \sigma_0^2\to\infty σ02→∞ 时,后验均值会退化成极大似然均值;后验方差 σ 2 ~ = σ 2 / N \widetilde{\sigma^2}=\sigma^2/N σ2 =σ2/N,效果如下图所示。