机器学习---一元线性回归（实战）

1.数据集展示

导入相关包

import numpy as np
from matplotlib import pyplot as plt

载入数据，是一个99行2列的数据

#载入数据
data = np.genfromtxt("data.csv",delimiter=",")
print(data)

2.定义损失函数和梯度下降法3.333

#学习率learning rate
lr = 0.0001
#截距
b=0
#斜率
k=0
#最大迭代个数
epochs=50
#最小二乘法
def compute_error(b,k,x_data,y_data):
    totalError = 0
    for i in range(0,len(x_data)):
        totalError+=(y_data[i]-(k*x_data[i]+b))**2
    return totalError /float(len(x_data))/2

def gradient_descent_runner(x_data,y_data,b,k,lr,epochs):
    #计算总数据量
    m = float(len(x_data))
    #循环epochs次
    for i in range(epochs):
        b_grad=0
        k_grad=0
        #计算梯度的总和再求平均
        for j in range(0,len(x_data)):
            b_grad+=(1/m)*((k*x_data[j]+b)-y_data[j])
            k_grad += (1/m) * (x_data[j])*(((k*x_data[j]+b)-y_data[j]))
        #更新b和k
        b = b-(lr*b_grad)
        k = k-(lr*k_grad)
    return b,k

3.可视化

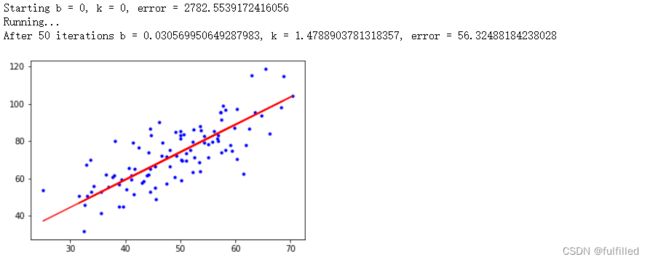
print("Starting b = {0}, k = {1}, error = {2}".format(b, k, compute_error(b, k, x_data, y_data)))
print("Running...")
b, k = gradient_descent_runner(x_data, y_data, b, k, lr, epochs)
print("After {0} iterations b = {1}, k = {2}, error = {3}".format(epochs, b, k, compute_error(b, k, x_data, y_data)))

# 画图
plt.plot(x_data, y_data, 'b.')  #"b是蓝色 .表示用点表示"
plt.plot(x_data, k*x_data + b, 'r')
plt.show()

4.使用Sklearn

from sklearn.linear_model import LinearRegression
import numpy as np
from matplotlib import pyplot as plt
data = np.genfromtxt("data.csv",delimiter=",")
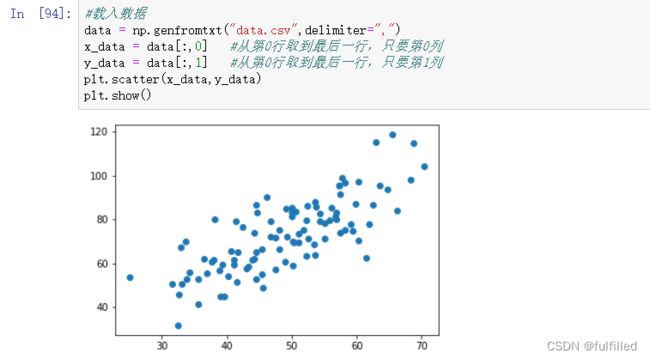
x_data=data[:,0]
y_data=data[:,1]
plt.scatter(x_data,y_data)
plt.show
print(x_data.shape)
x_data = data[:,0,np.newaxis]
y_data = data[:,1,np.newaxis]
#创建并你和模型
model = LinearRegression()
model.fit(x_data,y_data)
#画图
plt.plot(x_data,y_data,'b .')
plt.plot(x_data,model.predict(x_data),'r')
plt.show