NLP 第五周 语言模型，bert（2）

BERT类预训练语言模型

我们传统训练网络模型的方式首先需要搭建网络结构，然后通过输入经过标注的训练集和标签来使得网络可以直接达成我们的目的。这种方式最大的缺点就是时间长，因为我们对于模型权重的初始化是随机的，相当于一切从0开始学，如果我们能够在将训练集输入到模型之前先对权重进行预训练（pre train）,使其权重提前具备我们训练的某些规律，就好像我们在学习cv之前要求我们学习机器学习一样，其目的都是打基础，当然你预训练的数据需要和你的任务多多少少有所关联，你学cv之前你跑去学化学那就噶了。

我们进行预训练的数据需要是无标注文本的数据。无标注数据不等于是无标签数据，无标注是指不需要人为在训练之前就对样本进行标签或其他数据的标记，比如我们上面所用到通过前n个字符预测下一个字符，我们输入进去的只是单纯的文本，但是我们在网络里面通过文本自身从文本中提取出来了训练数据和标签，这就是无标注文本。我们在预训练上的目的只是通过前n个字对后一个字符进行预测，但是我们可以通过这个功能扩展到多个领域，这就是上面说的打基础。

NLP中预训练模型对无标注文本进行的处理一般有两种
①完形填空
其原理类似于我们上面的预测后一个字符。我们需要对一个文本中的一段话中的某个字符替换成这种token，选择替换的字符可以按照一定的规则，并且这段话里面可以不止替换一处，然后将替换后的文本输入网络，训练的数据是对处的字符作为标签进行学习。

②句子关系预测
其本质是一个二分类问题，我们将文本中的一段话从一处截断，然后输入到网络里面需要它来判断截断的两边是前后句的关系，也就是此时预测的标签为True。我们利用相同的手法，将文本中不同段话从一处截断，然后将每段话的前后句都与对方组合，比如A前配B后，B前配C后，前配后即可，只要保证不和自己的另一端组合就行，然后预测的标签设置为False，也就是说此时前后两段话并不存在前后句关系，相当于前后句没有逻辑关系：

这里的三个token是告诉网络句首，断点，句末的，作用与sos近似。

BERT的本质

BERT的本质是一种文本表征，也就是对文本的一种向量化，将文本中的文字转化为了可以用来计算和训练的向量。

对于文本的向量化而言，word2vec（词向量）也具备相同的功能，其原理就是单纯地对文本中的每一个字都进行了编码，如果我们改变每个字符的顺序，但是由于字符映射的数字是不变的，那么每个字符对应的编码并不会因此而改变。所以我们称word2vec是静态的。
但是BERT不同的是，我们在经过embedding层之后还要经过transformer结构，其输出的维度维度是不变的，可以暂时简单的认为一个输入的编码对应一个transformer的输出。transformer的特点决定了你输入字符编码的顺序不同，它对应的输出也会不同，如果我们把transformer的输出当作是对字符的二次编码，那么每个字符的编码会由于你输入顺序的不同而发生改变，相当于我们在编码里面假如了字符位置的特点，这样就更有利于我们探寻句子中字符的关系。所以BERT这种随着位置不断变化的编码我称之为动态的。这种方法的最大好处就是有效解决了一词多义的问题。

BERT结构-Encoder

我们用DETR里面Encoder做横向对比来比较二者的不同与相同（肯定相同更多一点）

输入预处理embedding模块
NLP方向

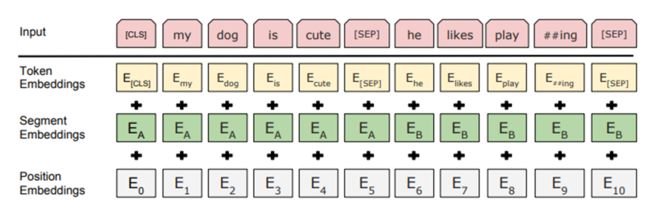
NLP方面的编码非常方便，如果我们采用断句的方式（其实断句这两个字并不准确，应该是连接两个句子的形式，这两个句子可以不是一句话通过断句来得到的，我只需要能够体现前后句关系就行）输入一句话到embedding层，那么每一个字符就被编码一次，到了中文里面就是一个字进行编码（当然加上了首尾和断句符号）。其具体步骤分为三步：

• 手下通过通常的embedding层进行编码即可，没有什么需要增强的
• 为不同的句子添加不同的segment编码（segment又叫做段，段落），以告诉网络这是两句话
• 最后为每一个字符添加唯一的能够显示位置的位置编码，以告诉网络每一个字符的位置信息，对于位置编码的讨论之前的博客已经深入讨论过了

需要说明的是，segment编码和position编码都是规定成训练的或者固定的，只要能够满足编码符合你设置的初衷就可以了。

如果我们输入进来的字符串有20个字符，那么三层编码的大小均为[20,768]，这样的话三者相加以后大小还是[20,768]，以此作为进入到encoder模块的输入

CV方向

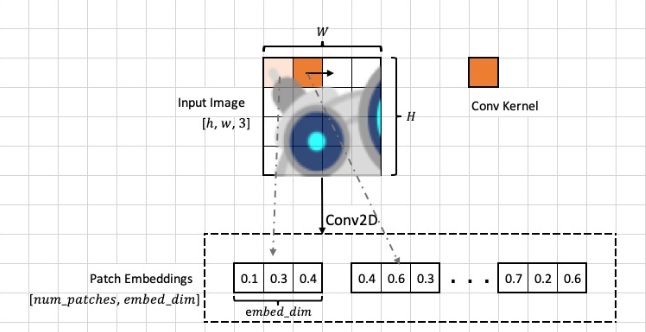
我们最简单的做法是按照如图的规则，对一张图分成等大的16个小方格，然后将每一个小方格里面的像素拿出来利用全连接层进行维度的映射到我们指定的embed_dim,也就是我们在embedding中的input_dim。这种操作可以用卷积来代替，将上面的图片进行尺寸大小为小方格尺寸，步长为小方格尺寸的卷积，然后设置卷积核的个数为input_dim，可以有相同的效果。在更复杂的网络结构中，我们会先使用一个backbone网络结构来专门处理输入进来的图像，例如DETR结构中使用的resnet53作为backbone，然后将得到的特征图中的每一个特征点当作是NLP中对每一个字符的编码再加上我们设置的位置编码position embedding之后输入进encoder里面。

这二者最大的区别我认为输入的含义不同，NLP中编码的含义就纯粹是编码并且，我们利用的就是embedding对字符进行编码，然后加上一些其他的东西，但是在CV中我们的主体是图片的特征，此时运用embedding仅仅是辅助我们进行位置编码，甚至大多数时候位置编码都是固定的，还用不上embedding。

attention计算模块
NLP与CV方向
其实只要规定了输入，那么encoder里面的流程都是一样的
NLP和CV各自提供了一套PPT，这两版结合起来的效果是非常不错的。
在DETR代码里面我们输入进encoder层里面的shape为[576,2,256],其中576是24x24，也就是特征图的宽高，2是batch，256是input_dim，它这个顺序是为了满足封装好的api，如果我们在解释原理的时候就直接用[576,256]来举例就方便多了。就代表一共有576个字符或特征点，input_dim为256。

首先将输入分别经过三个全连接层Wq，Wk，Wv（q表示query，k表示key，v表示value），对于映射到的维度数，源码中保持维度不变，但是这里为了方便理解，我们设置为100，也就是说得到的Q，K，V的shape均为[576,100]：

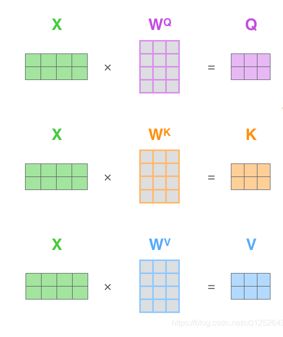
然后Q和K的转置进行矩阵乘法，即[576,100] dot [100,576]=[576,576]。我们可以推理一下结果中第一行是如何得到的，首先[576,100]中的第一行表示第一个字符的特征1，第二行表示第二个字符的特征1…[100,576]中的第一列表示第一个字符的特征2，第二列表示第二个字符的特征2…如此一来，相当于我们用一个字符的特征1与所有字符（包括它自己）的特征二相矩阵乘，每次结果都是一个矩阵对应位置相乘求和之后的一个数，所以[576,576]中的第一行就是第一个字符的特征1与所有字符的特征二矩阵乘之后的576个数，第二行就是第二个字符的特征1与所有字符的特征二矩阵乘之后的576个数…由于这576个数是由某一个字符的特征1与所有字符的特征2计算得到的结果，即这个数是二者作用的结果，所以给它取一个名字：注意力。代表这个注意力是反映二者联系的一种表示：

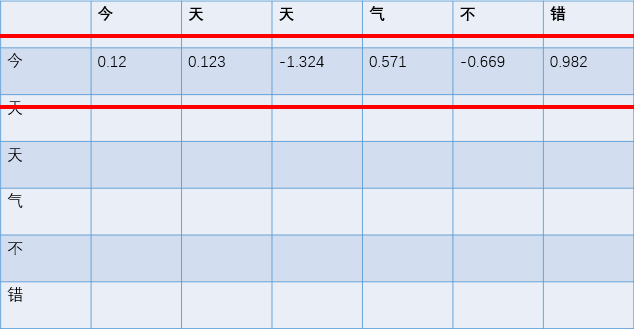
在得到每一个字符对所有字符的注意力之后，我们需要将它反馈给网络，这个时候就需要用到V，V的shape依然是[576,100]，可以说是字符的特征三。我们希望某一个字符对其他字符的注意力大的时候就影响这个字符多一点，反之则少一点。所以我们将注意力矩阵[576,576]与V[576,100]，这样的话得到原始的输出依然是[576,100],但是含义已经变了，此时的第一行是各个字符的特征三[100,]与第一个字符对各个字符的注意力进行加权求和之后得到的，相当于是λ1*(100,)+λ2*(100,)+λ3(100,)+…+λ576(100,)=(100,)

所以我们可以加深对注意力机制的理解：Q和K专门用来计算所有的注意力，而V才是整个注意力模块输出的模型，原始的V只是单纯地表示每个字符的特征，我们甚至可以直接理解为就是字符的编码，第一行就是第一个字符的编码，我们用什么来替换第一行的编码呢？用所有字符的加权和来作为替代，而权重则是第一个字符对所有字符的注意力，所以这也就解释了为什么BERT是动态的，因为只要某些字符的位置发生变化，那么所有字符对这些字符的注意力就会发生变化，又由于这些移动过后的字符的特征3也会发生改变，从而导致每一个字符最后输出的编码都会发生变化。

重点解释加粗的这句话

如果我们把位置编码去掉，就是单纯地将字符编码输入到encoder里面，你会发现最后只是单纯地增加网络的深度，而对于我们的语序问题没有丝毫的帮助。
因为如果只是单纯的字符编码，我们首先固定第一个字符不动，然后将某一个字符在同一句中的改变，假设第一个字符是A，改变位置的字符是B，B一开始在第6位，此时的B称作B6，后来移动到了第8位，此时的B称作B8。
然后A经过Wq以后得到A的特征1，B6经过Wk以后得到了特征2，B8经过Wk以后得到了特征2。其中B6和B8的特征二是一模一样的。
之后A与B6,B8分别矩阵乘得到了A对B6,B8的注意力，由于B6和B8的特征二是一样的，所以A对二者的注意力也是一样的
最后B6和B8经过Wv以后得到特征3，同时二者的特征3也是一样的，这样的话最后的加权结果由于二者的注意力是一样的，特征3又是一样的，所以对于字符A最后编码的输出影响是一样的。
这就是为什么不加位置编码最后并不会训练出语序的信息。

但是如果加了位置编码，就算你是相同的两个字，如上面的B6和B8，你本身字符的编码是一样，但是加上位置编码以后新的编码二者都是不一样的，从而两个相同的字符经过Wk以后得到的特征二就不一样，从而字符A对二者的注意力就不一样，又由于二者的特征3也不一样，所以最后对A的编码影响也不一样。

以上的机理是一个头的工作原理，也就是one head 而BERT是基于multi-head的结构。我们上面说过三个W矩阵映射到的维度是自己定义的，如果是one head，那么映射到的维度和input_dim是相同的，如果是多头注意力，假设10个头，那么每一个头映射的维度就是input_dim/10,那么一个头按照上面的逻辑最后得到的编码输出就是[576,10]，然后将每一个头拼起来组成[576,100]，然后会有一个新的全连接重新融合一下，维度不改变，依然是[576,100]。
多头机制的优势：bagging思想，也就是集成思想。将多个较弱的模型组合成一个较强模型。

最后公式中的根号，里面的dk就是就是映射的维度，在多头里面就是10，它的目的是将我们的输入的新的编码数字之间更加平滑，也就是方差减小趋于0。因为我们对softmax是逐行进行的，也就是每一个字符新的编码都会在自己内部进行softmax，如果这里面有的数字存在过大或者过小，那么我们在softmax了以后过小的数会趋于0，过大的数会趋于1，任何趋于极端的数据对于训练来说都是不利的，所以当我们改变了数据的方差，就可以使得在不改变二者大小的情况下，尽可能地把两个数的差距拉近，使其分布更加均匀。

随笔：归一化的目的是为了统一标准，因为不同的特征自己原始的标准是不同的，例如年龄从20到80岁，工资从5000到10万，这两种特征的范围是不一样的，所以梯度的更新会很难通知满足这两个条件，梯度大了工资可能回归地准确，但是年龄会出现在最优值附近来回横跳，梯度小了，年龄可能会回归得比较准确，但是对工资的修正幅度太小。所以归一化的目的就是将两类范围很大的数据标准统一。

第一部分的源码是通过输入的字符的索引来比较手动实现和调用接口实现的结果，其目的是熟悉bert的工作流程

diy_bert.py

bert = BertModel.from_pretrained(r"D:\code\自然语言处理NLP\第五周 语言模型，bert\下午\bert-base-chinese", return_dict=False)
state_dict = bert.state_dict()

BertModel是transformer包里面已经封装好的一个类，也就是最原始的bert结构，后来人们根据这个结构训练了很多种类的模型，训练方式就是根据前后文猜中间字和判断前后句的关系是否符合逻辑。这里采用的权重就是用这个模型训练好的判断中文的一个关系。权重地址为：https://huggingface.co/models

首先从保存了权重的文件夹里面将权重全部读取出来，相当于BertModel这个类只是简单的布置了所有网络层，现在我们将所有网络层都赋予了权重，所以此时的bert就是已经具备有效权重的各个网络层
这里的return_dict最好设置一下并且为False，要不然可能会报错。

然后使用类里面的state_dict()方法将参数全部提取出来得到state_dict

然后将模型设置为验证模式，目的仅仅是固定模型的BN和Dropout层，但是需要注意的是，model.eval()并不会阻止权重计算梯度，也不会阻止梯度的反向传播，只是因为我们自己没有设置.backward()和.step()，和eval()无关。

x = np.array([2450, 15486, 15167, 2110]) #通过vocab对应输入：深度学习
torch_x = torch.LongTensor([x])  #pytorch形式输入
seqence_output, pooler_output = bert(torch_x)

x是我们假装输入的一句话中四个字符映射的数字索引，由于是一维的，所以输入进去之前需要加一个[]。在x输入模型之后，得到的两个返回我们比较完手动实现的内容之后再做解释。

class DiyBert

class DiyBert:
    #将预训练好的整个权重字典输入进来
    def __init__(self, state_dict):
        self.num_attention_heads = 12
        self.hidden_size = 768
        self.num_layers = 12
        self.load_weights(state_dict)

必须与预训练模型里面的结构保持一致，这里设置的头数是12，编码的维度是768，所以可以盲猜下面的步骤会得到一个W矩阵映射的维度是768/12=64。
需要将encoder层堆叠12次，这个是唯一可以改变的参数，我可以选择使用训练好的12层encoder中的前几层的参数，但是这个参数也只能在这个自定义类里面改了才有效，因为人家的权重是在12层encoder已经训练完毕了，你改人家原本的json文件又没用，人家根本已经不需要训练了。

    def load_weights(self, state_dict):
        #embedding部分
        self.word_embeddings = state_dict["embeddings.word_embeddings.weight"].numpy()
        self.position_embeddings = state_dict["embeddings.position_embeddings.weight"].numpy()
        self.token_type_embeddings = state_dict["embeddings.token_type_embeddings.weight"].numpy()
        self.embeddings_layer_norm_weight = state_dict["embeddings.LayerNorm.weight"].numpy()
        self.embeddings_layer_norm_bias = state_dict["embeddings.LayerNorm.bias"].numpy()
        self.transformer_weights = []

这是输入embedding层的权重编码

        #transformer部分，有多层
        for i in range(self.num_layers):
            q_w = state_dict["encoder.layer.%d.attention.self.query.weight" % i].numpy()
            q_b = state_dict["encoder.layer.%d.attention.self.query.bias" % i].numpy()
            k_w = state_dict["encoder.layer.%d.attention.self.key.weight" % i].numpy()
            k_b = state_dict["encoder.layer.%d.attention.self.key.bias" % i].numpy()
            v_w = state_dict["encoder.layer.%d.attention.self.value.weight" % i].numpy()
            v_b = state_dict["encoder.layer.%d.attention.self.value.bias" % i].numpy()
            attention_output_weight = state_dict["encoder.layer.%d.attention.output.dense.weight" % i].numpy()
            attention_output_bias = state_dict["encoder.layer.%d.attention.output.dense.bias" % i].numpy()
            attention_layer_norm_w = state_dict["encoder.layer.%d.attention.output.LayerNorm.weight" % i].numpy()
            attention_layer_norm_b = state_dict["encoder.layer.%d.attention.output.LayerNorm.bias" % i].numpy()
            intermediate_weight = state_dict["encoder.layer.%d.intermediate.dense.weight" % i].numpy()
            intermediate_bias = state_dict["encoder.layer.%d.intermediate.dense.bias" % i].numpy()
            output_weight = state_dict["encoder.layer.%d.output.dense.weight" % i].numpy()
            output_bias = state_dict["encoder.layer.%d.output.dense.bias" % i].numpy()
            ff_layer_norm_w = state_dict["encoder.layer.%d.output.LayerNorm.weight" % i].numpy()
            ff_layer_norm_b = state_dict["encoder.layer.%d.output.LayerNorm.bias" % i].numpy()
            self.transformer_weights.append([q_w, q_b, k_w, k_b, v_w, v_b, attention_output_weight, attention_output_bias,
                                             attention_layer_norm_w, attention_layer_norm_b, intermediate_weight, intermediate_bias,
                                             output_weight, output_bias, ff_layer_norm_w, ff_layer_norm_b])

这个进入到encoder层以后的权重，因为encoder层可能不止一层。
之后由于我们需要复现两种方式的结果，所以我需要你每一个网络层里面的权重，现在单独拿出来说每一个网络层的权重没意义，等用到了他们各自的结合用途一起说明。

        #pooler层
        self.pooler_dense_weight = state_dict["pooler.dense.weight"].numpy()
        self.pooler_dense_bias = state_dict["pooler.dense.bias"].numpy()

这是最后接的分类层。

def forward

    #最终输出
    def forward(self, x):
        x = self.embedding_forward(x)

self.embedding_forward方法的作用就是将产生的三个编码和字符的编码进行相加最后返回

def embedding_forward

    def embedding_forward(self, x):
        # x.shape = [max_len]
        we = self.get_embedding(self.word_embeddings, x)  # shpae: [max_len, hidden_size]
        # position embeding的输入 [0, 1, 2, 3]
        pe = self.get_embedding(self.position_embeddings, np.array(list(range(len(x)))))  # shpae: [max_len, hidden_size]
        # token type embedding,单输入的情况下为[0, 0, 0, 0]
        te = self.get_embedding(self.token_type_embeddings, np.array([0] * len(x)))  # shpae: [max_len, hidden_size]
        embedding = we + pe + te
        # 加和后有一个归一化层
        embedding = self.layer_norm(embedding, self.embeddings_layer_norm_weight, self.embeddings_layer_norm_bias)  # shpae: [max_len, hidden_size]
        return embedding

self.word_embeddings是对所有字符进行编码的tensor对应的numpy，相当于是训练好的nn.Embedding的对象。所以self.word_embeddings是一个二维的numpy，这个可以单独拿出来看看，非常大：

[[ 0.02615827  0.01094903 -0.01868878 ...  0.09030139  0.0028486
   0.00642775]
 [ 0.00211436  0.02164099  0.00108996 ...  0.08090564  0.00178312
   0.02494784]
 [ 0.01467745  0.00050856  0.00283794 ...  0.08360939  0.01208044
   0.02821462]
 ...
 [ 0.03456404  0.00210567  0.00852101 ...  0.00853979  0.03371229
   0.00985317]
 [ 0.05406349  0.02890619  0.02626012 ...  0.0525924   0.06508742
   0.03532186]
 [ 0.02002425  0.00229523 -0.00892451 ...  0.07987329 -0.05615233
   0.02471835]]
(21128, 768)

def get_embedding(

    def get_embedding(self, embedding_matrix, x):
        return np.array([embedding_matrix[index] for index in x])

利用循环挨个调用x中各个索引，然后利用索引去self.word_embeddings里面找对应的编码最后返回，由于这里不涉及batch，所以返回的是二维数组，其shape为[4,768]。它就是我们的we，相当于是我们最原始的编码。

所以从这里可以看出来，任何一个网络模型不论是cv还是nlp，其处理数据的方式都是对一份样本进行的，其之所以可以允许输入的样本带batch，也不过是在网络里面将每一个样本单独过一遍网络然后将每个样本的输出再打包返回而已。

def embedding_forward
之后提取出我们需要的position embedding。

        pe = self.get_embedding(self.position_embeddings, np.array(list(range(len(x)))))  # shpae: [max_len, hidden_size]

其中self.position_embeddings就是训练好的位置编码，其shape为[512,768]，也就是说允许输入的一句话最多存在512个字符，然后按照顺序给每一个字符配备一个独一无二的位置编码，这个位置编码与字符本身的编码无关，只与你在一句话中的位置有关。
所以首先计算了输入进来的一句话有多少个字符，然后生成0到3的索引，最后根据索引从self.position_embeddings里面提取出位置编码，所以最后pe的shape=[4,768]

        te = self.get_embedding(self.token_type_embeddings, np.array([0] * len(x)))  # shpae: [max_len, hidden_size]

由于我们的训练任务中存在判断两个句子是否存在上下文关系，所以允许我们输入最多两句话，并分别对两句话中的字符在一个句子内赋予相同的编码。但是当我们的输入是一句话的时候，就只需要全体赋予第一个编码就行了。
self.token_type_embeddings的shape=[2.768]，由于只有一句话，所有后面的索引是4个0，即最后从self.token_type_embeddings中提取出来2当中的1四次，所以ts.shape=[4,768]

        embedding = we + pe + te
        # 加和后有一个归一化层
        embedding = self.layer_norm(embedding, self.embeddings_layer_norm_weight, self.embeddings_layer_norm_bias)  # shpae: [max_len, hidden_size]
        return embedding

将三个shape均为[4,768]的numpy进行相加得到的embedding 依然是[4,768]

之后将编码数组放进归一化函数里面

def layer_norm

    #归一化层
    def layer_norm(self, x, w, b):
        x = (x - np.mean(x, axis=1, keepdims=True)) / np.std(x, axis=1, keepdims=True)
        x = x * w + b
        return x

w也就是self.embeddings_layer_norm_weight，其提取的是embedding之后归一化中放大系数γ
b也就是self.embeddings_layer_norm_bias，其提取的是embedding之后归一化中的偏移系数β

之前在讨论eval的时候我们得出结论对于BN来说，训练的时候使用的每一组batch各自的均值和方差，但是在验证的时候使用的是之前训练集中所有样本的均值和方差。**看来LN不管是验证还是测试，使用的都是当前数据的方差和均值。**当然一定要注意它是在哪一维度进行的，对于BN而言是在将batch中的每一个样本中相同索引处的元素拿出来做归一化，我们把一个batch的样本当作是一本书，BN相当于是将每一页相同位置的字拿出来作为一个整体做的归一化。我们假设输入的tensor的shape为[b,c,hw],那么问题来了，我们知道的是把每一个样本中相同维度的元素拿去做归一化，但是每一个样本又不是一维的，到底是将一个样本中的hw中的每一个深度拍成一行以后以深度chw再取相同的位置进行归一化还是说每一个样本不排成一行就直接取对应位置的hw,以深度c进行归一化？其实没那么复杂，在源码里面其实仅仅是取了一个mean，然后dim设置为0，也就是我们说的第一种情况，dim为0，即把后面的[c,hw]看作是一个整体，自然效果就是和拍成一行一样的道理。
而LN则是在每一个样本内部做自归一化，相当于是一本书中每一页的所有文字作为一个整体做归一化。
在CV当中更多地使用BN，但是BN在batch很小的时候效果很差，因为batch太少，归一化的样本太小，不具有代表性。在NLP中更多得使用LN，因为一个batch相当于有很多句话，当我们使用BN的时候，会把每一句话的字符编码连接起来，然后再对应位置进行归一化，问题就在于，并不是每一句话的字符数目都是一样的，所以这个时候多余的字符实际是在和padding的字符进行归一化，自然效果就不佳了。所以采用LN，即一句话在自己的范围内进行归一化。

公式中β和γ的shape均为[768,]，我们输入进来的x的shape=[4,768]，所以这里LN绝不是将每一个字符的编码拍成一行，抛开两个参数的shape不谈，也不可能是拍成一行，因为每一句话的有效字符是不一样的，少的句子排成一行会有padding的编码填充，自然归一化起来就不靠谱。所以其实是每一个字符自己内部进行归一化，所有的字符都共用一组[768,]的γ和β。

回到计算上来，x的shape=[4，768]，首先计算x在第一个维度上面的均值，也就是768里面均值，并保持维度不变，所以np.mean返回的shape为[4,1]，同理求出方差，np.std返回的shape还是[4,1]

第一行代码得到的x.shape不变还是[4,768]
然后和w与b（shape均为[768,]）进行运算得到最后的x，shape还是[4,768]，这就是embedding_forward方法最后的输出

def forward(self, x):

sequence_output = self.all_transformer_layer_forward(x)

将x输入到encoder里面进行注意力的计算

def all_transformer_layer_forward

    #执行全部的transformer层计算
    def all_transformer_layer_forward(self, x):
        for i in range(self.num_layers):
            x = self.single_transformer_layer_forward(x, i)
        return x

将多个encoder层进行堆叠。其中i作为layer_index用来提取对应encoder层的权重

def single_transformer_layer_forward

    #执行单层transformer层计算
    def single_transformer_layer_forward(self, x, layer_index):
        weights = self.transformer_weights[layer_index]
        #取出该层的参数，在实际中，这些参数都是随机初始化，之后进行预训练
        q_w, q_b, \
        k_w, k_b, \
        v_w, v_b, \
        attention_output_weight, attention_output_bias, \
        attention_layer_norm_w, attention_layer_norm_b, \
        intermediate_weight, intermediate_bias, \
        output_weight, output_bias, \
        ff_layer_norm_w, ff_layer_norm_b = weights

这里的反斜杠并不代表不取，只是因为参数太多，我要换行书写，实际每一个参数我都要取出来。
我们之前说过，头的机制其实就是将完整的W矩阵按照头的数量进行平分，所以最后训练的W矩阵实际就是最初的最大的W矩阵。而W矩阵本质就是线性层，所以_w和_b其实就是线性层的权重和偏置。线性层的目的就是将编码的维度映射到另一维度，而字符的个数实际上只是决定矩阵的行数，所以我们在测试的时候字符个数多少都没关系，但是训练的时候会补齐到同一长度。

我们先说前6个参数
需要注意的是，_w的shape均为[768,768],这里后面的768才对应的输入维度，前面的768对应的是输出维度，和我们在定义linear层的时候是相反的（因为待会会求一个_w的转置）。而[4,768]中每一行与_w的转置的每一列做对应位数相乘再相加（实际就是线性计算）的时候都会加上一个偏置b，所以_w的转置有多少列，b就有多少个，也就是_w的行数，也即是我们需要映射到的输出维度大小。所以_b.shape=[768,]这个768是由输出维度大小决定的。

attention_output_weight, attention_output_bias
它们俩是将12个头的结果拼接之后融合特征的全连接层从权重和偏置，shape分别为[768,768],[768,]

attention_layer_norm_w, attention_layer_norm_b
它们俩是注意层输出和输入进行残差相加之后进行标准化的放大系数γ和偏移系数β,shape均为[768,]

intermediate_weight, intermediate_bias
它们俩是一个encoder层里面经过注意力机制层以后需要将维度大小通过线性层先放大，这次这个线性层的权重和偏置,shape分别为[3072,768],[3072]

output_weight, output_bias
它们俩是将放大的维度大小返回到原来维度大小的全连接层的权重和偏置，其shape分别为[768,3072],[768,]

ff_layer_norm_w, ff_layer_norm_b
它们俩是将经过两个全连接层的输出和未经过这两个全连接层的输入，即注意力机制的残差输出再进行一次残差计算以后最后做的LN时的γ和β，所以其shape均为[768,]

        #self attention层
        attention_output = self.self_attention(x,
                                q_w, q_b,
                                k_w, k_b,
                                v_w, v_b,
                                attention_output_weight, attention_output_bias,
                                self.num_attention_heads,
                                self.hidden_size)

def self_attention

    def self_attention(self,
                       x,
                       q_w,
                       q_b,
                       k_w,
                       k_b,
                       v_w,
                       v_b,
                       attention_output_weight,
                       attention_output_bias,
                       num_attention_heads,
                       hidden_size):
        q = np.dot(x, q_w.T) + q_b  # shape: [max_len, hidden_size]      W * X + B lINER
        k = np.dot(x, k_w.T) + k_b  # shpae: [max_len, hidden_size]
        v = np.dot(x, v_w.T) + v_b  # shpae: [max_len, hidden_size]
        attention_head_size = int(hidden_size / num_attention_heads)

x通过三个W矩阵需要得到对应的q，k，v，也就是将原始的编码维度映射到规定的编码维度，虽然这里不变。所以q的运算流程是：[4,768] dot[768,768].T=[4,768]+[768,]=[4,768],所以从这里面也可以看出来偏置实际上也是所有batch的所有字符都共用。k，v同理。但是这个步骤只是我们预想网络的工作原理，那么在实际训练中实际是创建了三个大的全连接层，然后将大的全连接层分成了head份，对应的head部分去计算加权和。具体可以参考DETR中自定义的qkv部分。

得到所有head的qkv以后计算每一个head分到的维度，也就是64

        # q.shape = num_attention_heads, max_len, attention_head_size
        q = self.transpose_for_scores(q, attention_head_size, num_attention_heads)
        # k.shape = num_attention_heads, max_len, attention_head_size
        k = self.transpose_for_scores(k, attention_head_size, num_attention_heads)
        # v.shape = num_attention_heads, max_len, attention_head_size
        v = self.transpose_for_scores(v, attention_head_size, num_attention_heads)

由于我们目前的qkv都是粘在一块的，多头注意力需要我们分开计算，所以transpose_for_scores的作用就是将qkv进行切分组合。

def transpose_for_scores

    #多头机制
    def transpose_for_scores(self, x, attention_head_size, num_attention_heads):
        # hidden_size = 768  num_attent_heads = 12 attention_head_size = 64
        max_len, hidden_size = x.shape
        x = x.reshape(max_len, num_attention_heads, attention_head_size)
        x = x.swapaxes(1, 0)  # output shape = [num_attention_heads, max_len, attention_head_size]
        return x

输入的x我们就当是q(shape=[4,768])，attention_head_size就是一个头对应的维度=64，num_attention_heads就是头数=12。

首先将q按照顺序，768中前64个位第一个头的，以此类推，所以仅仅用reshape我们就完成了第一步，x.shape=[4,12,64]

之后x转置成了[12,4,64]，这里剧透一下，q的shape是[12,4,64],之后k会被处理成[12,64,4]，因为头与头之间互不干扰，所以我们把12当作新的batch我们先不管，那么最后我们得到的shape就是[4,4]的，刚好对应4个字符和4个字符之间的注意力，同样这个注意力是由每个字符和所有字符分别相互作用得出来的。这也就是为什么最后需要转置成[12,4,64]的原因（因为用[12,64] dot [64,12]得到的是一个字符12个头之间的注意力，这是啥玩意儿啊…）

这里面还涉及到两个知识点

• np.swapaxes()和np.transpose()作用是相同的，但是前者括号里面只能出现两个轴，即只能进行两个轴之间的转置，如果需要类似于转(2,3,1)这种，则需要多次使用，后者则可以填写任意多的轴。
• np.matmul和np.dot的异同。首先两个函数都表示的是矩阵乘，就算是区别里面，也只是矩阵乘的时候选取的矩阵不同而已，当矩阵乘的双方都是2维数组的时候，二者的结果是一样的。不同点出在高维上，首先说简单的np.matmul，例如前后矩阵的shape为[2,2,3]和[2,3,2]那么最后结果的shape为[2,2,2]，它只会关注你最后两个维度能不能矩阵乘，如果可以，那就最后两个维度进行矩阵乘，其他维度以及维度大小不变，你就算再高维度，也仅仅是摆设。而np.dot中，[2,2,3]和[2,3,2]那么最后结果的shape为[2,2,2,2]，甚至维度都增加了，它的原理非常令人费解，它运算的主体还是最后两个维度，也即是[2,3]和[3,2]，但是它把矩阵运算分开了，首先前者的第一个3去乘后者的第一个3得到一个数，然后去乘后者的第二个3得到第二个数，这两个数组成了最深处dim的那个2(最后那个2)，然后取前者的第二个3去乘后者的第一个3得到一个数，然后去乘后者的第二个3得到第二个数(一样的步骤)，这两个2合起来得到了形状里面的倒数第二个2。又由于相乘的双方最外围各自还有一个0维度2，所以还有2x2中结果，所以最后的shape为[2,2,2,2]（目前看来这种运算逻辑毫无用处）。二者还有一点小不同的是matmul禁止矩阵和标量相乘，这个标量就是没有经过类似np.array的一个赤裸裸的数，而dot则会自动转为向量再做运算。

        # qk.shape = num_attention_heads, max_len, max_len
        qk = np.matmul(q, k.swapaxes(1, 2))
        qk /= np.sqrt(attention_head_size)
        qk = softmax(qk)
        # qkv.shape = num_attention_heads, max_len, attention_head_size
        qkv = np.matmul(qk, v)

将q[12,4,64]与k的转置[12,64,4]进行矩阵乘法得到[12,4,4]，相当于是12个头各自4x4的注意力矩阵
然后下一步除以了一个头维度的开方，其实这一步在哪里进行都可以了，目的是减少数据的方差

这里归一化是在求出注意力以后进行的，是按行的归一化，也就是归一化是在一个字符对所有字符的注意力的基础上进行的，其返回的是：

np.exp(x)/np.sum(np.exp(x), axis=-1, keepdims=True)

首先将attn中的所有数都取一个对数，所以np.exp(x)的shape还是[12,4,4]，然后由于我们是按照行里面的内容进行归一化，所以需要对最后一个维度进行相加，所以分母的shape为[12,4,1]，然后[12,4,4]/[12,4,1]，最后的结果还是[12,4,4]，但是已经替换成概率了。

最后attn与V进行矩阵乘来进行加权求和，即[12,4,4] dot [12,4,64]=[12,4,64]（再提醒一遍，譬如最后结果中的[4，64]中的第一行的64，其就是所有字符特征3中的64对位加权之后相加，这个权重就是第一个字符对对字符的注意力）

        # qkv.shape = max_len, hidden_size
        qkv = qkv.swapaxes(0, 1).reshape(-1, hidden_size)
        # attention.shape = max_len, hidden_size
        attention = np.dot(qkv, attention_output_weight.T) + attention_output_bias
        return attention

得到12个头的输出以后，我们需要将它们重新拼接成一个大的输出，所以先减输出qkv转置成[4,12,64],然后reshape成[4,768]

之后也像我们之前说过的那样，需要将仅仅是简单拼接的输出再经过一个全连接层进行特征的融合，attention_output_weight的shape=[768,768],第0个维度对应的是映射的维度，第1个维度对应的是输入的维度，attention_output_bias的shape=[768,]，每一个输出的维度最后线性运算的时候都会添加一个bias。

def single_transformer_layer_forward

        #bn层，并使用了残差机制
        x = self.layer_norm(x + attention_output, attention_layer_norm_w, attention_layer_norm_b)
        #feed forward层
        feed_forward_x = self.feed_forward(x,
                              intermediate_weight, intermediate_bias,
                              output_weight, output_bias)

在得到注意力层的输出以后需要先过一个残差网络，将注意力层的输入和输出相加之后再进行一个LN，这个LN层的γ，即attention_layer_norm_w，shape为[768,]，LN层的β，即attention_layer_norm_b，shape=[768,]。
最后返回的x的shape不变，还是[4,768]
之后又经过了两个全连接层先把维度放大，又把维度还原：

def feed_forward

    #前馈网络的计算
    def feed_forward(self,
                     x,
                     intermediate_weight,  # intermediate_size, hidden_size
                     intermediate_bias,  # intermediate_size
                     output_weight,  # hidden_size, intermediate_size
                     output_bias,  # hidden_size
                     ):
        # output shpae: [max_len, intermediate_size]
        x = np.dot(x, intermediate_weight.T) + intermediate_bias
        x = gelu(x)
        # output shpae: [max_len, hidden_size]
        x = np.dot(x, output_weight.T) + output_bias
        return x

既然是放大，那么用来放大的线性层的权重就是intermediate_weight，其shape=[3072,768]，对应的intermediate_bias的shape=[3072,]，用来缩小的线性层的权重是output_weight，其shape为[768,3072],对应的output_bias的shape=[768,]

首先将第一次残差时候的结果[4,768]经过第一个放大的全连接层以后shape变为[4,3072]，然后经过一个gelu的激活函数，其样式和relu差不多，但是公式变了很多，简单来说relu是一个分段函数，而gelu的公式为：xΦ(x)，相当于x乘了一个标准正态分布，其输入与输出的关系图为：

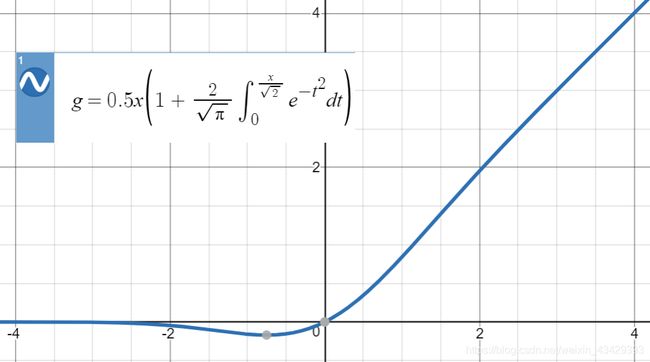
我们结合标准正太分布的图像可知，当x为负数时，那么后面便准正太的值也为正，但是不会超过1/2，那么总体呈现负数，但是当负得太多的时候，正太分布部分趋于0但是大于0，所以整体是趋于0但是小于0的地步，所以往后的曲线开始贴近x负半轴，而接近x正轴的负轴部分有一个小凹槽。
同时当x大于0时，由于正太部分不可能大于1，而x越大，越趋于1但是小于1，所以正半轴部分呈现类似于y=x的趋势，但是严格来说真实曲线是低于y=x的。

你让我怎么解释这个函数，我只能说他有类似于relu的特点但是比relu更加平滑，而且实际效果更好。

论文中将这个曲线的公式进行了近似化处理：

也就是下面我们用代码实现的那样

return 0.5 * x * (1 + np.tanh(math.sqrt(2 / math.pi) * (x + 0.044715 * np.power(x, 3))))

输入进去的x.shape=[4,3072]，相当于将每一个维度每一个数都做一个类似的运算过程，结果shape不变。

然后将输出放大过后的x再经过一个还原的全连接层得到最后返回的x，shape还原为[4,768]

def single_transformer_layer_forward

        #bn层，并使用了残差机制
        x = self.layer_norm(x + feed_forward_x, ff_layer_norm_w, ff_layer_norm_b)
        return x

最后一步就是将经过连续两个全连接层的输出和还未进入最后两个全连接层的输入，即注意力机制的残差输出再做一次残差，并将结果再一次用LN进行标准化，其中ff_layer_norm_w为进行标准化的γ，ff_layer_norm_b为进行标准化的β，其shape均为[768,]，如此一来一层的encoder就结束了。

一层是如此，利用def all_transformer_layer_forward可以继续套用下面层的encoder的参数，原理不变，所以只要改变self.num_layers，就可以任意使用训练好的encoder的任意层。

def forward

    #最终输出
    def forward(self, x):
        x = self.embedding_forward(x)
        sequence_output = self.all_transformer_layer_forward(x)
        pooler_output = self.pooler_output_layer(sequence_output[0])
        return sequence_output, pooler_output

那么all_transformer_layer_forward最后经过指定连续个数的encoder层以后返回的x还是[4,768]，维度和维度大小均未发生改变。

pooler_output_layer是设置的分类层，其实这里有一点信息之前没有来得及解释，那就是我们输入的句子的第一个字符，其实其本身并不是原始句子中的字符的映射数字，而是特意加在原始句子句首用来分类的一个token，它会和原始句子的字符进行同样的步骤，最后输出自己的综合注意力，例如我们就拿注意力最后输出的加权和x来说明，其shape为[4,768]，第一行就代表所有字符的特征三的加权和，权重就是第一个字符对所有字符的注意力，而实际就是cls token对所有字符的注意力，也就是第一行就是cls token对所有字符的特征三加注意力权重之和。所以把这一行单独拿出来做分类，相当于说认为它已经阅读过整体的特征了这么个意思。另外论文指出，是否额外加上这个cls token对训练结果影响不大。

所以self.pooler_output_layer中输入的shape仅仅是[768,]

def pooler_output_layer

    #链接[cls] token的输出层
    def pooler_output_layer(self, x):
        x = np.dot(x, self.pooler_dense_weight.T) + self.pooler_dense_bias
        x = np.tanh(x)
        return x

pooler_dense_weight和pooler_dense_bias的shape依然为[768,768]和[768,]
得到的x的shape不变，[768,]
然后经过一个tanh的激活函数，它的公式为：

它是难得的可以把结果映射到负数的激活函数，其范围为(-1,+1)
那么我们最后返回的x的shape不变，还是[768,],但是结果在被映射到-1和1之间。不是要做分类吗？为什么这里的shape不变呢？因为具体要分什么类是下游任务决定的，相当于这里只是先做一下分类的准备，单独先把网络层深入一下，之后只要直接接分类层就可以了。

def forward

        return sequence_output, pooler_output

最后返回的是几个连续encoder层的输出[4,768]和单独用来做分类任务的支线输出[768,]

diy_bert.py的最后

#自制
db = DiyBert(state_dict)
diy_sequence_output, diy_pooler_output = db.forward(x)
#torch
torch_sequence_output, torch_pooler_output = bert(torch_x)

# print(diy_sequence_output)
# print(torch_sequence_output)

print(diy_sequence_output.shape)
print(torch_sequence_output.shape)
print(diy_pooler_output.shape)
print(torch_pooler_output.shape)

输出shape为
(4, 768)
torch.Size([1, 4, 768])
(768,)
torch.Size([1, 768])

然后按照这个shape打印出来对应的位置，发现基本是一样的：

print(diy_sequence_output[-10:-1])
print(torch_sequence_output[0][-10:-1])
print(diy_pooler_output[:10])
print(torch_pooler_output[0][:10])

结果为：

	   [[ 0.11594751 -0.02066485 -0.4996819  ...  0.41767767  1.5785952
 		 -0.715069  ]
 		[ 0.38253862  0.05125671  0.3795222  ...  0.2413561   0.6288616
  		 0.14575967]
 		[ 0.4004798   0.07240379 -0.04194113 ...  0.35985705  0.66903
   		 0.17138824]]
tensor([[ 0.1160, -0.0212, -0.5076,  ...,  0.4161,  1.5789, -0.7164],
        [ 0.3805,  0.0512,  0.3781,  ...,  0.2404,  0.6275,  0.1468],
        [ 0.3985,  0.0724, -0.0436,  ...,  0.3577,  0.6685,  0.1720]],
       grad_fn=<SliceBackward0>)

		[-0.27626732  0.9648642  -0.98008376  0.9958502   0.3062773   0.8344301
 		-0.78546405 -0.729072    0.8875811   0.31061938]
 		
tensor([-0.2743,  0.9656, -0.9812,  0.9959,  0.3095,  0.8366, -0.7898, -0.7278,
         0.8866,  0.3109], grad_fn=<SliceBackward0>)

有个别差距的原因是numpy和torch在计算的时候保留的位数不同引起的。

下面一篇py是如何使用已经训练好的预训练模型bert来训练下游任务，我们的下游任务之前也使用过，即如果一个字符串里面有a或b或c，但是没有x或y或y，那么这类样本被归为一类，如果无前者但是有后者，再被归为一类，其他情况被归为第三类。

demo_with_bert.py

def main

def main():
    epoch_num = 15        #训练轮数
    batch_size = 20       #每次训练样本个数
    train_sample = 1000   #每轮训练总共训练的样本总数
    char_dim = 768         #每个字的维度
    sentence_length = 6   #样本文本长度
    vocab = build_vocab()       #建立字表

基本盘没变，这里也样本的字符长度固定死了，同时也改变了字符数字映射的字典，一开始用的是中文字符，这里为了减小运算量采用的是英文字符，这样一来一共就只有26个了。

def build_vocab

def build_vocab():
    chars = "abcdefghijklmnopqrstuvwxyz"  #字符集
    vocab = {}
    for index, char in enumerate(chars):
        vocab[char] = index + 1   #每个字对应一个序号
    vocab['unk'] = len(vocab)+1
    return vocab

仅仅是按照各个字母的顺序来给予它们对应的数字映射就可以了，最后形成的vacab中的元素一共有27个，因为还有unk的key。

def main

model = build_model(vocab, char_dim, sentence_length)    #建立模型

这个模型就是下面的类TorchModel
class TorchModel

class TorchModel(nn.Module):
    def __init__(self, input_dim, sentence_length, vocab):
        super(TorchModel, self).__init__()
        # 原始代码
        # self.embedding = nn.Embedding(len(vocab) + 1, input_dim)
        # self.layer = nn.Linear(input_dim, input_dim)
        # self.pool = nn.MaxPool1d(sentence_length)

        self.bert = BertModel.from_pretrained(r"F:\Desktop\work_space\pretrain_models\bert-base-chinese", return_dict=False)

        self.classify = nn.Linear(input_dim, 3)
        self.activation = torch.sigmoid     #sigmoid做激活函数
        self.dropout = nn.Dropout(0.5)
        self.loss = nn.functional.cross_entropy

    #当输入真实标签，返回loss值；无真实标签，返回预测值
    def forward(self, x, y=None):
        # 原始代码
        # x = self.embedding(x)  #input shape:(batch_size, sen_len) (10,6)
        # x = self.layer(x)      #input shape:(batch_size, sen_len, input_dim) (10,6,20)
        # x = self.dropout(x)    #input shape:(batch_size, sen_len, input_dim)
        # x = self.activation(x) #input shape:(batch_size, sen_len, input_dim)
        # x = self.pool(x.transpose(1,2)).squeeze() #input shape:(batch_size, sen_len, input_dim)

        sequence_output, pooler_output = self.bert(x)

        x = self.classify(pooler_output)
        y_pred = self.activation(x)
        if y is not None:
            return self.loss(y_pred, y.squeeze())
        else:
            return y_pred

首先我们利用将预训练模型的参数加载到预训练模型里面得到bert
其中input dim和cls token最后得到的维度大小要匹配上，也即是768，我们的分类数量是3，所以分类层映射到的维度为3

后面就非常正常了，我们先来回顾一下训练数据是如何产生的

def build_dataset

def build_dataset(sample_length, vocab, sentence_length):
    dataset_x = []
    dataset_y = []
    for i in range(sample_length):
        x, y = build_sample(vocab, sentence_length)
        dataset_x.append(x)
        dataset_y.append([y])
    return torch.LongTensor(dataset_x), torch.LongTensor(dataset_y)

这是一个batch的训练数据产生的步骤。

def build_sample

#从所有字中选取sentence_length个字
#反之为负样本
def build_sample(vocab, sentence_length):
    #随机从字表选取sentence_length个字，可能重复
    x = [random.choice(list(vocab.keys())) for _ in range(sentence_length)]
    #A类样本
    if set("abc") & set(x) and not set("xyz") & set(x):
        y = 0
    #B类样本
    elif not set("abc") & set(x) and set("xyz") & set(x):
        y = 1
    #C类样本
    else:
        y = 2
    x = [vocab.get(word, vocab['unk']) for word in x]   #将字转换成序号，为了做embedding
    return x, y

相当于是从字典里面随机抽6个字母组成一个训练样本，最后返回的x是一个一维列表，里面装的是抽取到的各个字母或者unk，y是一个数。然后将x里面的字母全部换成对应的数字映射存并返回就可以了

那么最后build_dataset返回的就是dataset_x和dataset_y均是二维的tensor，表示一个batch的训练数据

然后将这一个batch的训练数据输入到self.bert中得到对应的sequence_output（20，6，768）和pooler_output（20，768）

然后pooler_output经过线性层得到x.shape=[20,3]，表示20个样本的预测，最后经过激活函数得到预测值y_pred，如果有标签输入就计算误差，没有就是在验证。

后面的步骤就省略了。

tokenizer.py

在transformers这个包里面还有一个类BertTokenizer，是transformers自带的一个序列化工具

tokenizer = BertTokenizer.from_pretrained(r"F:\Desktop\work_space\pretrain_models\bert-base-chinese")

string = "咱呀么老百姓今儿个真高兴"
#分字
tokens = tokenizer.tokenize(string)
print("分字：", tokens)#分字： ['咱', '呀', '么', '老', '百', '姓', '今', '儿', '个', '真', '高', '兴']

#编码，前后自动添加了[cls]和[sep]
encoding = tokenizer.encode(string)
print("编码：", encoding)#编码： [101, 1493, 1435, 720, 5439, 4636, 1998, 791, 1036, 702, 4696, 7770, 1069, 102]
#这里所说的编码以及下面的编码都是指的是输入的字符在映射字典中的数字编码


#文本对编码, 形式[cls] string1 [sep] string2 [sep]
string1 = "今天天气真不错"
string2 = "明天天气怎么样"
encoding = tokenizer.encode(string1, string2)
print("文本对编码：", encoding)#文本对编码： [101, 791, 1921, 1921, 3698, 4696, 679, 7231, 102, 3209, 1921, 1921, 3698, 2582, 720, 3416, 102]

#同时输出attention_mask和token_type编码
encoding = tokenizer.encode_plus(string1, string2)
print("全部编码：", encoding)#全部编码： {'input_ids': [101, 791, 1921, 1921, 3698, 4696, 679, 7231, 102, 3209, 1921, 1921, 3698, 2582, 720, 3416, 102], 'token_type_ids': [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1], 'attention_mask': [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]}

BERT的优势

①预训练利用了大量的无标注文本数据
②相比于单纯的词向量而言，BERT的加工使得字符编码对应的输出结合了语境与字序
③Transformer模型结构具有很强的拟合能力，词与词之间的距离不会造成关系计算上的损失，比如马尔可夫假设，如果定语太长，容易造成有关系的两个字词构造不出联系，Transformer则不管你距离多远，都会计算到和你的注意力

BERT的劣势

①预训练需要时间，数据和机器（但是开源的模型缓解了这一问题）
②难以应用在生成式任务（这是由于bert训练的任务特点决定的，我们其中的任务是根据前后问预测中间的字，但是这种方式不适用于生成式任务，也就是给你信息让你来得到结果，相当于是单侧的）
③参数数量太大，运算复杂，满足不了部分真实场景性能需求（主要是运算较慢）
④没有下游任务做fine tune，效果依然不是很理想

GPT

其本质和bert几乎类似，主要在于训练任务的改变，GPT就仅仅是单纯地用句子前面所有的字来预测后面的字，相当于采用的是单向的原则。

GPT2

继续使用单项语言模型
略微对transformer机构进行改动
模型更深，更大，数据更多

Roberta

完全没有改变BERT的结构，仅仅是改变了模型的训练过程
①采用了更多的数据，更大的batch，更久的训练
②去掉了判断前后句逻辑的任务
③使用了更长的样本
④动态改变了mask位置（bert中mask的位置一开始是随机选取的，但是一旦选中了整个训练过程所有的epoch都使用的这个mask的位置，Roberta则每一轮训练都对不同的位置进行mask，间接增加了训练集的数量）

启示：挖掘旧的方法的潜力，有时比创新还要有效
能够最大限度的发挥一种算法的能力，也是算法工程师能力的一种体现

ALBERT

其主要的目的是为了解决BERT模型过大的问题，想办法减小参数量
①跨层的参数共享，即连续使用的encoder中使用相同的某些层，例如全连接层，第一个encoder使用以后再第二个encoder层使用的时候把这个全连接层再接上，相当于多个人用一双筷子，精度肯定会减小，但是减小不了多少，同时参数确可以成倍的减小
②Embedding层的因式分解，例如一开始的词表大小为3000，隐藏单元的个数为1024，如果映射的时候一共会出现30000x1024个参数，但是如果先把编码维度设置为512，然后再用512映射到1024，那么总共的参数只有30000x512+512x1024

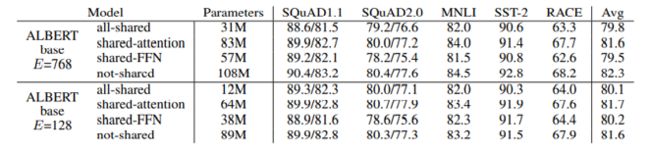
虽然工程角度来讲价值不大，但是证明了参数量并非模型能力的绝对衡量标准。

同时其在训练的时候也改变了训练任务，还是那个判断前后句的任务。因为原始任务中前后两句话关系不大，预测起来太简单了，所以讲现在将本来就是前后句关系的两句话颠倒顺序作为负样本，相当于将负样本预测起来更难了。

GPT3

1750亿参数量是GPT2的116倍，其他基本啥都没变

预训练的发展方向

①更多的数据，更大的模型
②不同的预训练任务
③尽可能适应更多的下游任务
④预训练模型训练完毕以后如何避免训练过多的下游数据，换句话说我们希望预训练模型拿来就能用

新的研究方向：Prompt

https://github.com/Jackfantas/Bert-Chinese-Prompt-Mask.git