狄利克雷语义增强的在线流文本聚类

狄利克雷语义增强的在线流文本聚类

本文参考： “An Online Semantic-enhanced Dirichlet Model for Short Text Stream Clustering”
论文连接：https://www.aclweb.org/anthology/2020.acl-main.70.pdf
GitHub：https://github.com/JayKumarr/OSDM

dirichlet过程先验知识

目标描述

$S_t=\{d_t{\}}_{t=1}^{\infty }$ 表示$d_t$表示t时刻到达的document，而每一个$d_t表示\{w_1,w_2,\dots ,w_n\}$,表示有n个word，而且每个document所包含的word的数量是不一样的。聚类任务的关键就是将相似的文章聚成几个类族，用公式来表示即为$Z=\{z_t{\}}_{t=1}^{\infty }$,其中$z_t$表示一个类别，即$z_t=\{d_1^{z_t},d_2^{z_t},\dots ,d_n^{z_t}\}$,有n篇文章属于$z_t$类别,注意每篇文章的类别只能是一个，故$z_i和z_j$之间没有交集。

先验知识Dirichlet过程

混合模型基础

如果用高斯混合模型举例来说，单个高斯模型，可以表示为$P(x|\theta )=\frac{1}{\sqrt{2\pi {\sigma }^2}}exp(-\frac{(x-\mu {)}^2}{2{\sigma }^2})$,如果x为高维数据，则是$P(x|\theta )=\frac{1}{2\pi {\sigma }^{D/2}|{\Sigma }^{1/2}|}exp(-\frac{(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )}{2})$,而高斯混合模型可以描述为$P(x|\theta )={\sum }_{k=1}^K{\alpha }_k\varphi (x|{\theta }_k)$，表示有k个单个高斯模型，用来描述多个属性，${\alpha }_k$表示观测数据集属于k个子模型的概率。

Dirichlet过程模型

Dirichlet分布是Beta分布在高维情形的推广，就是一个混合模型.现在介绍一下beta分布，在贝叶斯框架常作为概率的概率分布。举个例子如抛硬币，如果用贝叶斯分布求其后验分布p过程中，即$P(q|x)P(x)=P(q)P(x|q)$（求正面的概率，通过很少次数抛硬币实验次数是很难得出p=1/2这个结论),在这个例子中假如x为硬币的正面，我们可以假设先验概率p(q)为零到一的均匀分布，同时可以确定$P(x|q)$的分布，模拟n次抛硬币，P(x)无关可以舍弃，将等式右边式子整合既可以得到beta分布，最后为$P(q|x)=\frac{(x{)}^{\alpha -1}(1-x{)}^{\beta -1}}{B(\alpha ,\beta )}$。进一步升华，则可以假设是一个骰子，有六个面，则如同上面所说的混合模型一样，可以得到Direchlet模型，$Dir(X,\alpha )=\frac{{\prod }_i^d{x}_i^{\alpha -1}}{B(\alpha )}$，其中B是为了使概率为1的标准概率模型，是分子的积分。

产生Dirichlet过程三种方式

PUS

poly urn模型构造狄利克雷过程，假设我们有一个罐子，（初始时刻从base分布中取出一个球放入罐子中）从里面拿出一个球，如果是黑色，那么我们产生一个新的颜色球，并和原来的球一起放入罐子中，如果不是黑球那么再拿一个和这个球颜色一样的球放入罐子中，如果拿出的是黑球，不再是重新拿一个新的颜色，而是从base分布中随机选取一个颜色放入罐子中， 该过程可以描述为$p(G|\widehat{{\theta }_1},\dots ,\widehat{{\theta }_N})=DP(\alpha +N,\frac{1}{\alpha +N}(\alpha H+{\sum }_{i=1}^N\delta (\theta ,{\hat{\theta }}_i)))$。前面是一个参数，后半部分可以看为先验分布$G_0$。

CRP

中国餐馆构造狄利克雷模型，顾客进入餐馆可以按照一定的概率$\frac{n_k}{\alpha +N}$选择某个餐桌或者$\frac{\alpha }{\alpha +N}$新的餐桌，具体不再阐述。

stick breaking

使用折断模型也可以推出狄利克雷过程：[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

对于一根木棍，每次以不同比例$\tau$概率进行截断成俩节，则${\pi }_i={\tau }_i{\prod }_{j=1}^{i-1}(1-{\tau }_j)$,可以知道所有的$\pi$累加和为1。可以将$\pi$看做random probability measure，我们可以将其写为$\pi \sim GEM(\gamma )$,定义分布函数为$G(N)={\sum }_{k=1}^{\infty }{\pi }_k\delta (N-N_k),N_k\sim N_0$可以用以下方式来描述：
$N_k|\beta \sim Dir(\beta )$每一个类别的概率的概率分布
$z_d|\theta \sim Mult(\theta )$属于一个类别是多项分布

方法

模型简述

本论文有俩个主要亮点：

• 通过捕获单词的重合率获取语义信息，因此word产生和重合权重被考虑到其中
• 通过一个一个实例进行聚类，而不是通过一个batch进行聚类，逐步的动态更新每次到达的document的数量。

模型公式

属于已存在的类别概率

过去通过定义document和class之间的相似度来进行分类，这个相似度会设置阈值，但是这对文本流来说是很难定义相似度衡量方法。假设document是由DPMM生成的，同时我们考虑了语义特征，和术语的独特性。具体公式如下：
$p(z_d=z|z,d,\alpha ,\beta )=(\frac{m_z}{D-1+\alpha D})\cdot (\frac{{\prod }_{w\in d}{\prod }_{j=1}^{N_d^w}(n_z^w\cdot lC{F}_w+\beta +j-1)}{{\prod }_{i=1}^{N_d}(n_z+V\beta +i-1)})\cdot (1+{\sum }_{w_i\in d\wedge w_j\in d}c{w}_{ij})$
对于公式中第一部分来说，$m_z$是z类别中的document数量，而D是已经分好的类中的所有的文本数量，这个公式的意义即CRP中选择占有的桌子。第二部分的公式是狄利克雷过程，$n_z^w$是z类别中w单词的数量，$N_d^w$是document中w的数量，V代表已分类中单词的数量，$n_z$表示类别中所有单词的数量，$n_z^w$代表类别中w单词的数量。ICF计算术语在过去已分类文本中的比重，计算公式是$log(\frac{|Z|}{|w\in Z|}$其中|z|代表类别的数量。z产生document的概率可以表示为$p(d|N_z)={\prod }_{w\in d}Mult(w|N_z)$我们定义在类别和文章之间的语义权重。第三部分公式中
其中$n_{d^{\prime }}^{w_i}$表示在document中的单词的频率计数。

属于新类的概率

接下我们定义，如何产生一个新的类，新的类公式由DPMM,超参数在类中应该的动态变化故，$\theta \sim GEM(\alpha D)$,公式如下：[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1qXbSQE6-1666415337046)(img3.png)]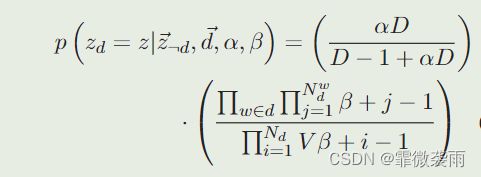

通过最终比较是新类还是属于过去的某一类概率哪一个比较大来最终进行判断，该document属于哪一个类别。

代码私聊 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vqCq0bJY-1666416095025)(https://bkimg.cdn.bcebos.com/pic/6609c93d70cf3bc79f3da3719d55ada1cd11738bfcab?x-bce-process=image/watermark,image_d2F0ZXIvYmFpa2UxODA=,g_7,xp_5,yp_5#pic_center)]