数据结构与算法(java版)第二季 - 6 并查集

需求分析

假设是存在n个村庄,有些村庄之间是有连接的路,有些村庄之间是不存在连接的路,如下图所示:

 设计一个数据结构,能够快速执行下面两个操作:

①查询两个村庄之间是否有连接的路[遍历一下数组之中的元素,看看他们是否在一个数组之中]

②连接两个村庄

数组、链表、平衡二叉树、集合（Set）？ ---- 查询、连接的时间复杂度都是：O(n)

并查集能够办到查询、连接的均摊时间复杂度都是 O (α (n))  ， α (n) < 5

并查集（Union Find）

并查集也叫作不相交集合（ Disjoint Set ）

并查集有两个核心的操作:

查找(Find):查找相应的元素是属于哪一个集合(这里的集合并不是指Set这种数据结构,而是广义的数据结构)

合并(Union):将两个元素所在的集合的元素变成一个集合

有2种常见的实现思路

 Quick Find

✓ 查找（Find）的时间复杂度： O(1)

✓ 合并（Union）的时间复杂度： O(n)

 Quick Union(建议使用)

✓ 查找（Find）的时间复杂度： O(logn) ，可以优化至 O (α (n))  ， α (n) < 5

✓ 合并（Union）的时间复杂度： O(logn) ，可以优化至 O (α (n))  ， α (n) < 5

如何存储数据

◼ 假设并查集处理的数据都是整型，那么可以用整型数组来存储数据

上面的含义是:0 1 3 属于集合1, 2 属于集合2, 4属于集合5, 5 6 7 属于集合6.上面是使用相应的箭头划分出来集合的归属范围的. 上面之中的4 5 6 7 也是可以看成是一个集合的过程.

因此，并查集是可以用数组实现的树形结构（二叉堆、优先级队列也是可以用数组实现的树形结构).

读懂小马哥教程之中一些定义,之后就是开始相应的代码的编写:

①接口

②初始化 

在进行相应的初始化的时候,每个元素各自属于一个集合,而且是一个单元素的集合.

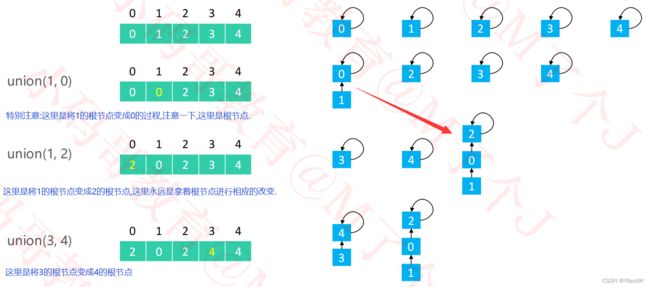
Quick - Union的一个操作:

这里的union操作室将前面的父节点变成后面的节点

注意上面的union(1,2)的操作过程,就是将左边的父节点,变成后面的节点.

上面的是元素,下面是相应的根节点.

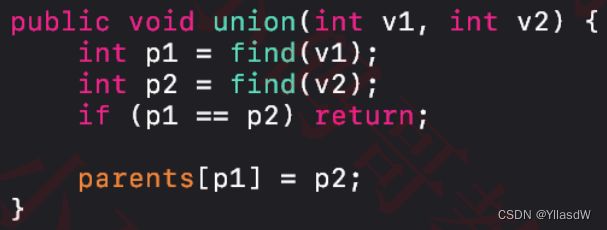
 相应的代码部分单独讲解:
这里不能简简单单将v1的父节点直接变成v2,应当将节点都是v1的变成相应的v2的节点.上面的合并操作的代码复杂度是O(n).

Quick  - Find

代码实现

package com.mj.union;

public class UnionFind1 {
	//声明相应的父节点
	protected int[] parents;

	//进行相应的Union的构造
	public UnionFind1(int capacity) {
		if (capacity < 0) {
			throw new IllegalArgumentException("capacity must be >= 1");
		}
		
		parents = new int[capacity];
		for (int i = 0; i < parents.length; i++) {//将自己的元素放入到自己之中,就是自己只想自己的过程.
			parents[i] = i;
		}
	}
	
	/**
	 * 查找v所属的集合（根节点）
	 * @param v
	 * @return 根节点
	 */
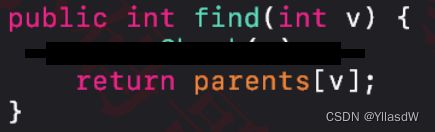
	public  int find(int v)
	{
		rangeCheck(v);
		return parents[v];

	}

	/**
	 * 合并v1、v2所在的集合
	 */
	public void union(int v1, int v2)
	{
		int p1 = find(v1);
		int p2 = find(v2);
		
		if(p1 == p2) return;
		
		for(int i = 0;i < parents.length;i++)
		{
			if(parents[i] == p1)
			{
				parents[i] = p2;
			}
		}
	}
	
	/**
	 * 检查v1、v2是否属于同一个集合
	 */
	public boolean isSame(int v1, int v2) {
		return find(v1) == find(v2);
	}

	protected void rangeCheck(int v) {
		if (v < 0 || v >= parents.length) {
			throw new IllegalArgumentException("v is out of bounds");
		}
	}
}

主函数之中的测试代码:

public static void main(String[] args) {
		UnionFind1 uf = new UnionFind1(12);
		uf.union(0, 1);
		uf.union(0, 3);
		uf.union(0, 4);
		uf.union(2, 3);
		uf.union(2, 5);

		uf.union(6, 7);

		uf.union(8, 10);
		uf.union(9, 10);
		uf.union(9, 11);

		System.out.println(uf.isSame(0,6));
		System.out.println(uf.isSame(0,5));
	}

为了简单,这里我们直接定义一个接口,变成一个抽象类:

package com.mj.union;

public abstract class UnionFind {
	//声明相应的父节点
	protected int[] parents;

	//进行相应的Union的构造
	public UnionFind(int capacity) {
		if (capacity < 0) {
			throw new IllegalArgumentException("capacity must be >= 1");
		}
		
		parents = new int[capacity];
		for (int i = 0; i < parents.length; i++) {//将自己的元素放入到自己之中,就是自己只想自己的过程.
			parents[i] = i;
		}
	}
	
	/**
	 * 查找v所属的集合（根节点）
	 * @param v
	 * @return 根节点
	 */
	public abstract int find(int v);

	/**
	 * 合并v1、v2所在的集合
	 */
	public abstract void union(int v1, int v2);
	
	/**
	 * 检查v1、v2是否属于同一个集合
	 */
	public boolean isSame(int v1, int v2) {
		return find(v1) == find(v2);
	}

	protected void rangeCheck(int v) {
		if (v < 0 || v >= parents.length) {
			throw new IllegalArgumentException("v is out of bounds");
		}
	}
}

使用类对于上面的方法进行实现

QuickFind的实现

package com.mj.union;

/**
 * Quick Find
 * @author Y
 *
 */
public class UnionFind_QF extends UnionFind {
	public UnionFind_QF(int capacity) {
		super(capacity);
	}

	/*
	 * 父节点就是根节点
	 */
	public int find(int v) {
		rangeCheck(v);
		return parents[v];
	}

	/**
	 * 将v1所在集合的所有元素，都嫁接到v2的父节点上
	 */
	public void union(int v1, int v2) {
		int p1 = find(v1);
		int p2 = find(v2);
		if (p1 == p2) return;
		
		for (int i = 0; i < parents.length; i++) {
			if (parents[i] == p1) {
				parents[i] = p2;
			}
		}
	}
}

Quick Union ------ Union的实现

这里的QuickUnion的实现是如下所示:

时间复杂度：O(logn)

注意:这里的union的使用是将前面的跟节点变成后面的一个根节点的过程.,这里应当区分其与quickFind的区别.通过上面图示,是很好区分二者的区别的.

Quick Union ------ Find的操作

会得到如下的结果:

◼ find(0) == 2

◼ find(1) == 2

◼ find(3) == 2

◼ find(2) == 2

◼ 时间复杂度： O(logn)

 相应的代码实现的过程是:

代码的实现:

package com.mj.union;

/**Quick Union
 * @author Y
 */
public class UnionFind_QU extends UnionFind {

	public UnionFind_QU(int capacity) {
		super(capacity);
	}

	//通过parent链条不断地向上找，直到找到根节点
	 
	public int find(int v) {
		rangeCheck(v);
		while (v != parents[v]) {
			v = parents[v];
		}
		return v;
	}

	// 将v1的根节点嫁接到v2的根节点上
	 
	public void union(int v1, int v2) {
		int p1 = find(v1);
		int p2 = find(v2);
		if (p1 == p2) return;
		parents[p1] = p2;
	}

}

在开发之中我们是一般使用union的。

Quick Union - - 优化

◼ 在Union的过程中，可能会出现树不平衡的情况，甚至退化成链表

◼ 有2种常见的优化方案

 基于size的优化：元素少的树 嫁接到 元素多的树

 基于rank的优化 ：矮的树 嫁接到 高的树     ----------------   乍一听是差不多的，但是元素的多少和树的高矮是没有关系的

基于Size的代码：

package com.mj.union;

/* Quick Union - 基于size的优化
 * @author Y
 */
public class UnionFind_QU_S extends UnionFind_QU {
	//首先是定义相应的元素的个数
	private int[] sizes;

	public UnionFind_QU_S(int capacity) {
		super(capacity);
		
		sizes = new int[capacity];//这就是以capacity为根节点的元素是多少

		for (int i = 0; i < sizes.length; i++) {//初始的根节点
			sizes[i] = 1;
		}
	}

	//我们这里只是进行优化Union的过程，Find的过程是不用动的
	//将v1的根节点嫁接到v2的根节点上
	public void union(int v1, int v2) {
		int p1 = find(v1);
		int p2 = find(v2);
		if (p1 == p2) return;
		
		//元素的多少进行嫁接
		if (sizes[p1] < sizes[p2]) {
			parents[p1] = p2;
			sizes[p2] += sizes[p1];
		} else {
			parents[p2] = p1;
			sizes[p1] += sizes[p2];
		}
	}

}

基于size的算法是如下所示：可能会导致不平衡现象的出现。

基于Rank的优化

 代码如下所示:

package com.mj.union;

public class UnionFind_QU_R extends UnionFind_QU {
	private int[] ranks;

	public UnionFind_QU_R(int capacity) {
		super(capacity);

		ranks = new int[capacity];
		for (int i = 0; i < ranks.length; i++) {
			ranks[i] = 1;
		}
	}
	
	public void union(int v1, int v2) {
		int p1 = find(v1);
		int p2 = find(v2);
		if (p1 == p2) return;
		
		//ranks之后是不需要进行任何的改动
		if (ranks[p1] < ranks[p2]) {
			parents[p1] = p2;
		} else if (ranks[p1] > ranks[p2]) {
			parents[p2] = p1;
		} else {
			parents[p1] = p2;
			ranks[p2] += 1;
		}
	}
}

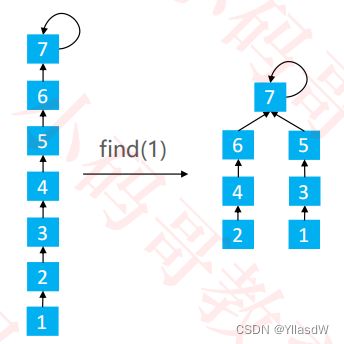
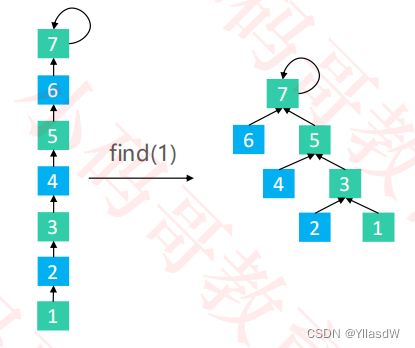
路径压缩

虽然是有了基于Rank的优化,树会相对平衡一些.但是随着Union的次数的增多,树的高度是不断变高的.进而导致相应的find操作变慢,尤其是底层节点(因为find是不断向上找到跟节点的)

路径压缩:在使用find的时候,将路径上所有的节点都是指向根节点,从而降低树的高度的过程.

 代码如下所示:

package com.mj.union;

//基于rank的优化 - 路径压缩(Path Compression)

public class UnionFind_QU_R_PC extends UnionFind_QU_R {

	public UnionFind_QU_R_PC(int capacity) {
		super(capacity);
	}
	
	@Override
	public int find(int v) { // v == 1, parents[v] == 2
		rangeCheck(v);
		if (parents[v] != v) {
			parents[v] = find(parents[v]);
		}
		return parents[v];
	}
}

上面的路径压缩使得路径上的所有节点都指向根节点,所以实现成本比较高.

还是存在两种更加好的方法,不但能够降低树高,实现成本也是比路径压缩低的:路径分裂(Path Spliting) 路径减半(Path Having)

路径分裂

路径分裂：使路径上的每个节点都指向其祖父节点（parent的parent）

这里的高度变化程度不是很大,因此这种变化的成本是比较低的.

package com.mj.union;
//基于Rank的优化---路径优化
public class UnionFind_QU_R_PS extends UnionFind_QU_R {

	public UnionFind_QU_R_PS(int capacity) {
		super(capacity);
	}
	
	@Override
	public int find(int v) { 
		rangeCheck(v);
		while (v != parents[v]) {
			int p = parents[v];
			parents[v] = parents[parents[v]];//父节点变成祖父节点
			v = p;
		}
		return v;
	}
}

路径减半

路径减半：使路径上每隔一个节点就指向其祖父节点（parent的parent）

package com.mj.union;

// 基于Rank的优化 - 路径减半(Path Halving)

public class UnionFind_QU_R_PH extends UnionFind_QU_R {

	public UnionFind_QU_R_PH(int capacity) {
		super(capacity);
	}
	
	@Override
	public int find(int v) { 
		rangeCheck(v);
		while (v != parents[v]) {
			//逐次使用这个过程进行相应的叠加
			parents[v] = parents[parents[v]];
			v = parents[v];

		}
		return v;
	}
}

一般使用路径压缩、分裂或减半 + 基于rank或者size的优化

自定义对象的使用

◼ 之前的使用都是基于整型数据，如果其他自定义类型也想使用并查集呢？

 方案一：通过一些方法将自定义类型转为整型后使用并查集（比如生成哈希值）

 方案二：使用链表+映射（Map)

package com.mj.union;

import java.util.HashMap;
import java.util.Map;
import java.util.Objects;

public class
GenericUnionFind {
	private Map> nodes = new HashMap<>();

	//进行相应的初始化
	public void makeSet(V v) {
		if (nodes.containsKey(v)) return;
		nodes.put(v, new Node<>(v));
	}
	
	/**
	 * 找出v的根节点
	 */
	private Node findNode(V v) {
		Node node = nodes.get(v);
		if (node == null) return null;
		while (!Objects.equals(node.value, node.parent.value)) {
			node.parent = node.parent.parent;
			node = node.parent;
		}
		return node;
	}
	
	public V find(V v) {
		Node node = findNode(v);
		return node == null ? null : node.value;
	}
	
	public void union(V v1, V v2) {
		Node p1 = findNode(v1);
		Node p2 = findNode(v2);
		if (p1 == null || p2 == null) return;
		if (Objects.equals(p1.value, p2.value)) return;
		
		if (p1.rank < p2.rank) {
			p1.parent = p2;
		} else if (p1.rank > p2.rank) {
			p2.parent = p1;
		} else {
			p1.parent = p2;
			p2.rank += 1;
		}
	}
	
	public boolean isSame(V v1, V v2) {
		return Objects.equals(find(v1), find(v2));
	}
	
	private static class Node {
		V value;
		Node parent = this;
		int rank = 1;
		Node(V value) {
			this.value = value;
		}
	}
}