图神经网络（二）—GCN-pytorch版本代码详解

写在前面…
在研究生的工作中使用到了图神经网络，所以平时会看一些与图神经网络相关的论文和代码。写这个系列的目的是为了帮助自己再理一遍算法的基本思想和流程，如果同时也能对其他人提供帮助是极好的~博主也是在学习过程中，有些地方有误还请大家批评指正！

• github: https://github.com/OuYangg/GNNs

1 GCN基本介绍

• 论文标题：Semi-supervised classification with graph convolutional networks
• 作者：Thomas N. Kipf, Max Welling

GCN是一种基于谱域的图卷积神经网络。在spectral-based GCN模型中，会将每个节点的输入看作是信号，并且在进行卷积操作之前，会利用转置后的归一化拉普拉斯矩阵的特征向量将节点的信号进行傅里叶变换，卷积完了之后再用归一化拉普拉斯矩阵的特征向量转换回来。其中，将信号进行傅里叶变换的公式如下：
$$F(x)=U^{T}x$$
$$F^{-1}(x)=Ux$$
其中，$U$为归一化拉普拉斯矩阵$L=I_N-D^{-1/2}A{D}^{-1/2}$的特征向量。基于卷积理论，卷积操作被定义为：
$$gx=F^{-1}(F(g)F(x))=U(U^{T}g{U}^{T}x),$$
其中，$U^{T}g$为谱域的过滤器，若将$U^{T}g$简化为一个可学习的对角矩阵$g_w$，则有
$$gx=U{g}_w{U}^{T}x$$.
一个比较有名的spectral-based GCN模型是ChebNet的思想就是利用切比雪夫多项式来作为参数，得到
$$gx=\sum _{k=0}^K{w}_k{T}_k(L)x$$,
其中，$T_k(x)=2x{T}_{k-1}(x)-T_{k-2}(x),T_0(x)=1,T_1(x)=x$，$L=\frac{2}{{\lambda }_{max}}L-I_N$，${\lambda }_{max}$为$L$的最大特征值。

GCN是在ChebNet的基础上，令$K=1$，${\lambda }_{max}\approx 2$，得到
$$g_{w}x=w_{0}x+w_{1}Lx$$，其中，$L$被简化为了$D^{-1/2}A{D}^{-1/2}$，得到
$$g_{w}x=w(I_N+D^{-1/2}A{D}^{-1/2})x$$，令$I_N+D^{-1/2}A{D}^{-1/2}=D^{-1/2}A{D}^{-1/2}$，得到
$$H=\sigma \{D^{-1/2}A{D}^{-1/2}XW\}$$
其中，$X\in R^{N\times F}$为输入，即节点的特征矩阵，$W\in R^{F\times F^{\prime }}$为参数，$F^{\prime }$为第一层输出size，$\sigma$为ReLU激活函数。以上就是GCN的前向传播公式。

上面一大堆公式看不懂其实不要紧！！
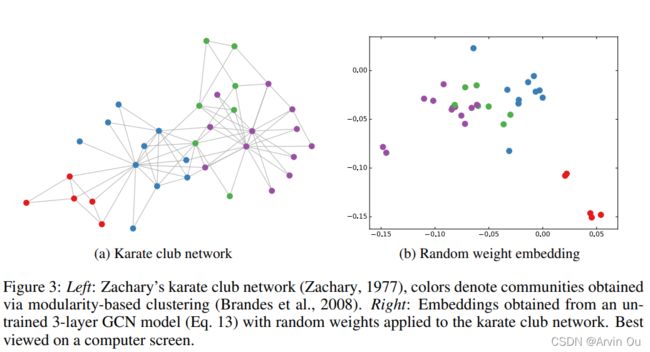
大家只要知道GCN是一个比较简单且好用的图神经网络模型就可以了。至于有多好用，可以看下面这张图，下图为未经过训练的三层GCN，其中所有的参数均为随机的参数，可以看到他还没训练就可以对节点有一个非常准确的分类，非常的震惊有没有。

2 代码解析

• 代码参考地址：pyGCN
• 导入所需的库

import math
import time
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import scipy.sparse as sp
import argparse

2.1 导入数据

def encode_onehot(labels):
	"""使用one-hot对标签进行编码"""
    classes = set(labels)
    classes_dict = {c: np.identity(len(classes))[i, :] for i, c in
                    enumerate(classes)}
    labels_onehot = np.array(list(map(classes_dict.get, labels)),
                             dtype=np.int32)
    return labels_onehot

def normalize(mx):
    """行归一化"""
    rowsum = np.array(mx.sum(1))
    r_inv = np.power(rowsum, -1).flatten()
    r_inv[np.isinf(r_inv)] = 0.
    r_mat_inv = sp.diags(r_inv)
    mx = r_mat_inv.dot(mx)
    return mx

def sparse_mx_to_torch_sparse_tensor(sparse_mx):
    """将一个scipy sparse matrix转化为torch sparse tensor."""
    sparse_mx = sparse_mx.tocoo().astype(np.float32)
    indices = torch.from_numpy(
        np.vstack((sparse_mx.row, sparse_mx.col)).astype(np.int64))
    values = torch.from_numpy(sparse_mx.data)
    shape = torch.Size(sparse_mx.shape)
    return torch.sparse.FloatTensor(indices, values, shape)

def load_data(path="./cora/", dataset="cora"):
    """读取引文网络数据cora"""
    print('Loading {} dataset...'.format(dataset))
    idx_features_labels = np.genfromtxt("{}{}.content".format(path, dataset),
                                        dtype=np.dtype(str)) # 使用numpy读取.txt文件
    features = sp.csr_matrix(idx_features_labels[:, 1:-1], dtype=np.float32) # 获取特征矩阵
    labels = encode_onehot(idx_features_labels[:, -1]) # 获取标签

    # build graph
    idx = np.array(idx_features_labels[:, 0], dtype=np.int32)
    idx_map = {j: i for i, j in enumerate(idx)}
    edges_unordered = np.genfromtxt("{}{}.cites".format(path, dataset),
                                    dtype=np.int32)
    edges = np.array(list(map(idx_map.get, edges_unordered.flatten())),
                     dtype=np.int32).reshape(edges_unordered.shape)
    adj = sp.coo_matrix((np.ones(edges.shape[0]), (edges[:, 0], edges[:, 1])),
                        shape=(labels.shape[0], labels.shape[0]),
                        dtype=np.float32)

    # build symmetric adjacency matrix
    adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)

    features = normalize(features)
    adj = normalize(adj + sp.eye(adj.shape[0]))

    idx_train = range(140)
    idx_val = range(200, 500)
    idx_test = range(500, 1500)

    features = torch.FloatTensor(np.array(features.todense()))
    labels = torch.LongTensor(np.where(labels)[1])
    adj = sparse_mx_to_torch_sparse_tensor(adj)

    idx_train = torch.LongTensor(idx_train)
    idx_val = torch.LongTensor(idx_val)
    idx_test = torch.LongTensor(idx_test)

    return adj, features, labels, idx_train, idx_val, idx_test

2.2 GCN模型框架

class GCNLayer(nn.Module):
	"""GCN层"""
    def __init__(self,input_features,output_features,bias=False):
        super(GCNLayer,self).__init__()
        self.input_features = input_features
        self.output_features = output_features
        self.weights = nn.Parameter(torch.FloatTensor(input_features,output_features))
        if bias:
            self.bias = nn.Parameter(torch.FloatTensor(output_features))
        else:
            self.register_parameter('bias',None)
        self.reset_parameters()

    def reset_parameters(self):
    	"""初始化参数"""
        std = 1./math.sqrt(self.weights.size(1))
        self.weights.data.uniform_(-std,std)
        if self.bias is not None:
            self.bias.data.uniform_(-std,std)

    def forward(self,adj,x):
        support = torch.mm(x,self.weights)
        output = torch.spmm(adj,support)
        if self.bias is not None:
            return output+self.bias
        return output

class GCN(nn.Module):
	"""两层GCN模型"""
    def __init__(self,input_size,hidden_size,num_class,dropout,bias=False):
        super(GCN,self).__init__()
        self.input_size=input_size
        self.hidden_size=hidden_size
        self.num_class = num_class
        self.gcn1 = GCNLayer(input_size,hidden_size,bias=bias)
        self.gcn2 = GCNLayer(hidden_size,num_class,bias=bias)
        self.dropout = dropout
    def forward(self,adj,x):
        x = F.relu(self.gcn1(adj,x))
        x = F.dropout(x,self.dropout,training=self.training)
        x = self.gcn2(adj,x)
        return F.log_softmax(x,dim=1)

2.3 评估与训练

def accuracy(output, labels):
    preds = output.max(1)[1].type_as(labels)
    correct = preds.eq(labels).double()
    correct = correct.sum()
    return correct / len(labels)

def train_gcn(epoch):
    t = time.time()
    model.train()
    optimizer.zero_grad()
    output = model(adj,features)
    loss = F.nll_loss(output[idx_train],labels[idx_train])
    acc = accuracy(output[idx_train],labels[idx_train])
    loss.backward()
    optimizer.step()
    loss_val = F.nll_loss(output[idx_val],labels[idx_val])
    acc_val = accuracy(output[idx_val], labels[idx_val])
    print('Epoch: {:04d}'.format(epoch+1),
          'loss_train: {:.4f}'.format(loss.item()),
          'acc_train: {:.4f}'.format(acc.item()),
          'loss_val: {:.4f}'.format(loss_val.item()),
          'acc_val: {:.4f}'.format(acc_val.item()),
          'time: {:.4f}s'.format(time.time() - t))


def test():
    model.eval()
    output = model(adj,features)
    loss_test = F.nll_loss(output[idx_test], labels[idx_test])
    acc_test = accuracy(output[idx_test], labels[idx_test])
    print("Test set results:",
          "loss= {:.4f}".format(loss_test.item()),
          "accuracy= {:.4f}".format(acc_test.item()))

if __name__ == '__main__':
    # 训练预设
    parser = argparse.ArgumentParser()
    parser.add_argument('--no-cuda', action='store_true', default=False,
                        help='Disables CUDA training.')
    parser.add_argument('--fastmode', action='store_true', default=False,
                        help='Validate during training pass.')
    parser.add_argument('--seed', type=int, default=42, help='Random seed.')
    parser.add_argument('--epochs', type=int, default=200,
                        help='Number of epochs to train.')
    parser.add_argument('--lr', type=float, default=0.01,
                        help='Initial learning rate.')
    parser.add_argument('--weight_decay', type=float, default=5e-4,
                        help='Weight decay (L2 loss on parameters).')
    parser.add_argument('--hidden', type=int, default=16,
                        help='Number of hidden units.')
    parser.add_argument('--dropout', type=float, default=0.5,
                        help='Dropout rate (1 - keep probability).')

    args = parser.parse_args()
    np.random.seed(args.seed)
    adj, features, labels, idx_train, idx_val, idx_test = load_data()
    model = GCN(features.shape[1],args.hidden,labels.max().item() + 1,dropout=args.dropout)
    optimizer = optim.Adam(model.parameters(),lr=args.lr,weight_decay=args.weight_decay)
    for epoch in range(args.epochs):
        train_gcn(epoch)

结果如下：

参考资料

[1] Hamilton W L, Ying R, Leskovec J. Inductive representation learning on large graphs[J]. arXiv preprint arXiv:1706.02216, 2017.
[2] https://github.com/tkipf/pygcn