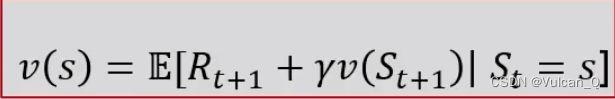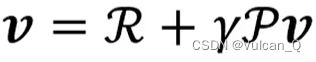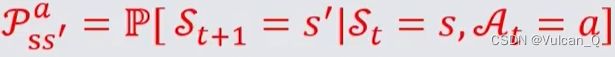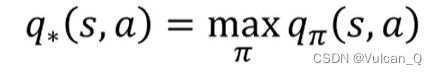【从RL到DRL】强化学习基础（二）——马尔可夫决策过程与相关贝尔曼方程

绪言

马尔可夫决策过程（Markov decision processes，MDP）

• MDP是强化学习问题在数学上的理想化形式
• MDP中的环境使完全可观测的
• 几乎所有的强化学习问题都可以在数学上表示为马尔可夫决策过程

---

马尔可夫过程

马尔可夫性质

未来只与现在有关，与过去无关

定义：状态St具有马尔可夫性，当且仅当：
给定当前时刻状态，将来与历史无关，状态是对过去的充分统计:对于马尔可夫状态与其后继状态s’，他们的状态转移概率定义为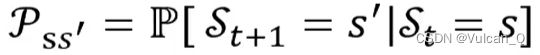：。状态转移矩阵P定义了马尔可夫状态s到其所有后继状态s’的转移概率：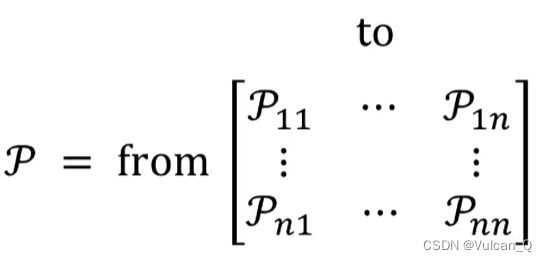
矩阵的每一行总和为1.矩阵的维度为|s|·|s|，其中s为状态数量

马尔可夫过程

• 马尔可夫过程是一种无记忆的随机过程
• 马尔可夫过程可以分为三类
  • 时间、状态都离散的马尔可夫过程（马尔可夫链）
  • 时间连续、状态离散的马尔可夫过程（连续时间的马尔可夫链）
  • 时间、状态都连续的马尔可夫过程
  • 

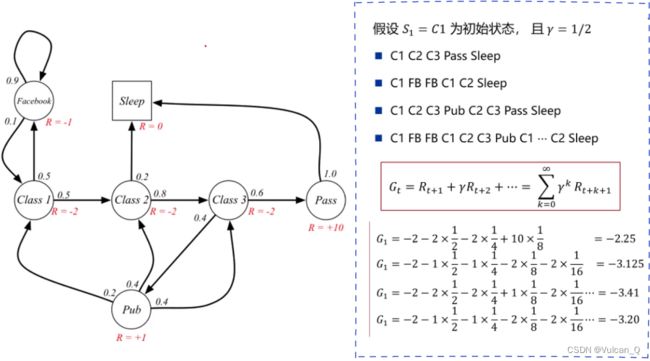
定义： 从初始状态S1 = c1开始，我们可以从马尔可夫链中采样一些子序列，每个子序列又称为幕（Episodes）。在有“幕”或者有“回合”概念的状态集中，一般都会有一个“终止状态”，在马尔可夫链中一般用方框表示，状态转移箭头“只进不出”。

---

马尔可夫奖励过程（Markov Reward Process，MRP）

马尔可夫奖励过程是具有价值的马尔可夫链

马尔可夫奖励过程（Markov Reward Process，MRP）由元组(S,P,R,γ)构成

• S是有限状态的集合

• P是状态转移矩阵

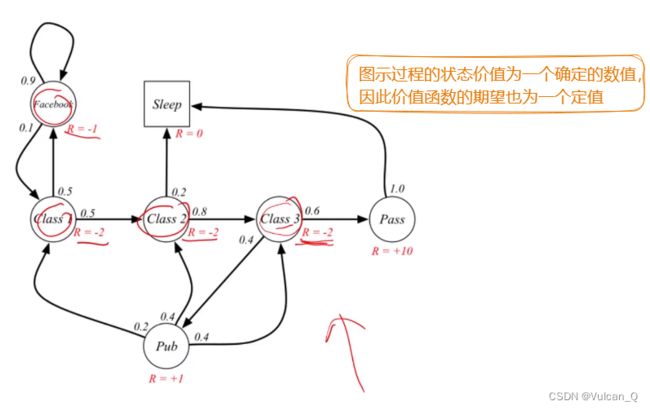
• Rs是奖励函数，Rs = E[Rt+1 | St = s]。到达St这个状态后系统给智能体的奖励值的期望（系统给分具有一定的随机性）

• γ是折扣因子，γ∈[0 , 1]

• 回报：在一个马尔可夫奖励过程中，从t时刻的状态St开始，直至终止状态时，所有奖励的衰减之和G_t称为 回报（Return），其中即用到了折扣因子γ

• 折扣率或者衰减率γ的作用

  • 避免有环的马尔可夫过程计算收益时出现无限循环
  • 从金融投资回报的角度讲，即时奖励比延时奖励更吸引人
  • 动物/人类行为中都表现出对及时奖励的偏好
  • 可以表达未来的不确定性
  • γ ∈ [0,1]，γ = 0表示只看眼前收益

回报计算举例：

价值函数

价值函数V(s)给出状态s的长期价值(long-term value)
价值函数输入为某个状态，输出为这个状态的价值

在马尔可夫奖励过程之中，一个状态的 期望回报 被称为这个状态的价值函数

价值函数是强化学习的核心概念

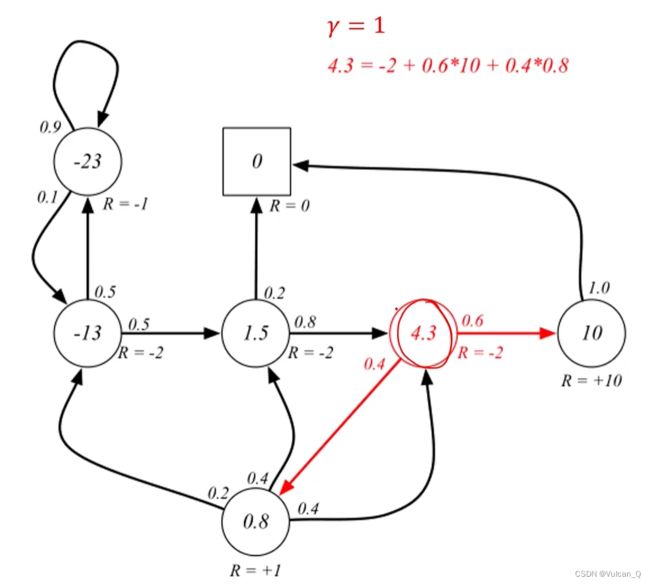
贝尔曼方程(Bellman Equation)

求解价值函数

• 当前状态的价值 = 求期望 (到达当前状态时的得分 + 衰减率×下一个状态的价值）
• 方程本身：

价值函数

即时奖励Rt+1

后继状态的折扣值γv（S _t+1）

• 推导过程：

• 应用举例：

• 为了真正计算过程中的方便，往往使用贝尔曼方程的变形形式：其中Pss’为状态转移矩阵。上文的状态结构计算如下：

• 如果各个状态的价值不满足贝尔曼方程意味着这个价值函数不能描述这个状态，说明计算有误

• 贝尔曼方程的矩阵表示：

• 其中v是一个列向量，每个状态对应一个条目：

贝尔曼方程的解

在上文的矩阵表达形式下，贝尔曼方程就变成了一个可以直观求解的矩阵方程。该方程是线性方程 ，可以直接求解：
对于 |S| 个状态，计算复杂度为O(|S|^3)，直接求解仅适用于小型马尔可夫奖励过程 ，对于大型的MRP，有很多迭代方法，例如：

• 动态规划（Dynamic Programming）
• 蒙特卡洛评估(Monte-Carlo evaluation)
• 时序差分学习（Temporal-Difference Learning）

---

马尔可夫决策过程（MDP）

基本组成与概念

马尔可夫决策过程（MDP）是具有决策的马尔可夫奖励过程（MRP），其所有状态满足马尔可夫性质。马尔可夫决策过程由元组(S,A,P,R,γ) 构成。

• S是有限状态的集合
• A是有限动作的集合
• P是状态转移矩阵：
• Rs是奖励函数：
• γ是折扣因子，γ∈[0,1]

应用举例：

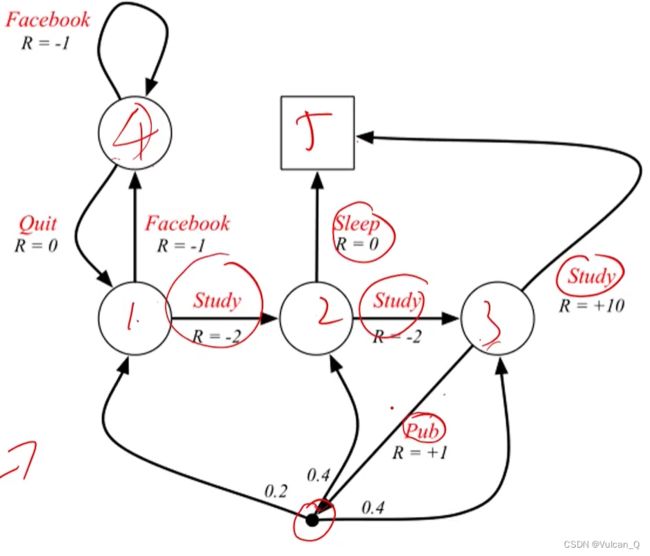
对应的动作集合：A={Study,Pub,Sleep,Quit,Facebook}。注意上图中四线交汇的节点含义：说明在其他状态通过某一动作到达该节点处后，下一个状态由系统决定，即该节点表示一个系统随机选择的过程。

策略

定义：策略π是一个函数，表示输入状态为s的情况下采取动作a的概率：

• 策略完全定义了智能体的行为
• 马尔可夫决策过程中，策略仅取决于当前状态（而不是历史记录）

给定一个马尔可夫决策过程：M = (S,A,P,R,γ) 和一个策略π。状态序列S₁,S₂……是一个马尔可夫随机过程π>。状态和奖励序列是一个马尔可夫奖励过程π,R^π,γ>

• 上式中 P^π_ss’ 意为从状态s到状态s’的转移概率，右侧的求和符号内， π(a|s) 意为处于状态s时智能体执行动作a的概率，P^a_ss’意为智能体执行完动作a后，由系统决定的从状态s到状态s’的概率（可以理解为与前文所述的节点处，需要系统依概率决定下一状态）
• R^π_ss’与R^a_ss’的含义与之类似

MDP的价值函数

定义·状态价值函数：
在马尔可夫决策过程中，一个价值函数V_π(S)是从状态s出发，遵循策略π得到的期望回报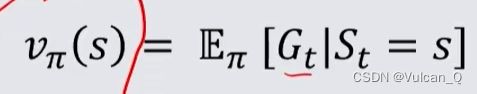
定义·动作价值函数：
在马尔可夫决策过程中，一个动作价值函数q_π(s,a)是从状态s开始，遵循策略π，对当前状态s执行动作a得到的期望回报：

状态价值函数可以用来评判不同的动作决策π的优劣，而动作价值函数则描述的是具体的动作策略π内执行不同动作的优劣，可以用来对具体的策略进行优化

贝尔曼期望方程（Bellman Expectation Equation）

前文的贝尔曼方程没有动作的概念

• 状态函数可以分解为：即时奖励 + 后继状态×后继状态折扣值：
• 动作价值函数可以进行类似分解：
• 动作价值函数与状态价值函数的联系：状态价值函数在意义上其实包含了两层随机性，即：接下来执行动作的随机性 + 执行完相应动作后到状态s’的随机性。因此，如果我们在状态s时指定了要执行的动作a后，状态价值函数的第一层随机性就被拿掉了，这时它便与动作价值函数意义相同，这一关系用数学表示为：
• 递推公式：
• 联立递推：
• 计算应用

最优价值函数(Optimal Value Function)

最优价值和函数是所有策略产生的状态价值函数中，使状态s价值最大的函数：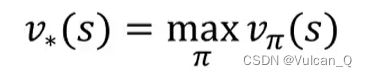

• 最优动作价值函数是指所有策略产生的动作价值函数中，使状态-行为对价值最大的函数：
• 最优价值函数明确了MDP的最优可能表现 ，一旦最优价值函数知晓，则认为MDP已完成求解

最优策略（Optimal Policy ）

定义：策略之间的偏序，当且仅当对于任意的状态s都有：
定义：最优策略。在有限状态和动作的MDP中，至少存在一个策略不劣于其他所有的策略，即这就是最优策略。所有的最优策略有相同的最优状态价值函数与动作价值函数

• 寻找最优策略
  • 可以通过最大化q_*(s,a)来找到最佳策略（arg表示取的是使得后面式子最大时的a的值），这个方法也是一种 贪婪策略
  • 任何MDP始终都有确定性的最佳策略
  • 如果我们知道q_*(s,a)，我们将立即获得最优策略

贝尔曼最优方程

这是基于前文的贪婪策略变形后的方程，因为此时的π(a|s)只有0或1，省略变形后便直接等于max函数的值。同理可以得到最优动作价值函数的变形形式：
递推后
计算应用：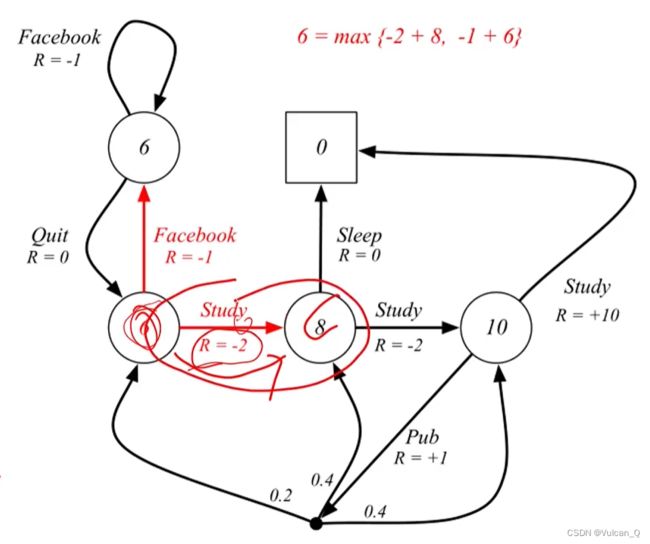

求解贝尔曼最优方程

• 贝尔曼最优方程是非线性的
• 不能使用与策略优化相同的直接矩阵解决方案
• 通过一些迭代方法来解决
  • 价值迭代
  • 策略迭代
  • Q学习
  • Sarsa

---

总结

贝尔曼期望方程总结

贝尔曼最优方程总结