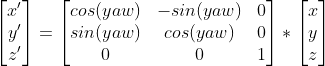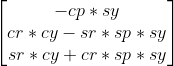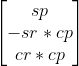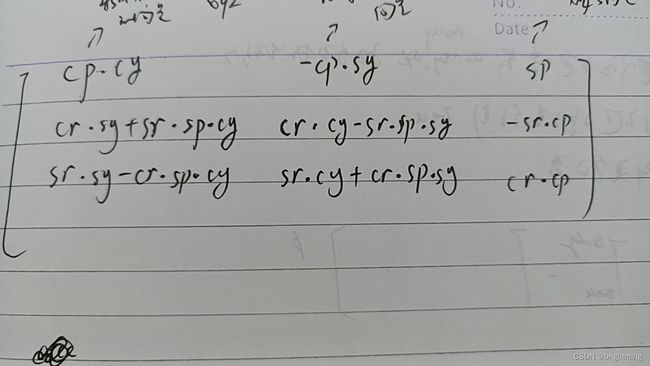利用imu估计roll、pitch的理解

这次好好的梳理一下。
先从两种旋转开始说起。

**参考：https://blog.51cto.com/xxpcb/2903395**

1、坐标轴不动，向量绕原点旋转后的关系

旋转前坐标为(x,y,z)，旋转后为(x',y',z')。

旋转情况为：

绕z轴旋转yaw，绕y轴旋转pitch，绕x轴旋转roll。

这里明显可知道，每次都是绕的是固定的原坐标系轴，即可以说是外旋。这个也是这里可以统一概念的地方。

那么旋转矩阵为：

绕z轴旋转后的情况是：

在这个基础上，绕y轴旋转：

在这个基础上，绕x轴旋转：

把矩阵乘起来，就得到完整的矩阵。从等式可以看出来，是Rot_old_to_new的。

2、坐标轴旋转，原来的向量在新的坐标系下的表示

这个本质上，要计算出新的坐标轴的基向量在原坐标轴的表示。

在上一步已经知道了向量的旋转前后的表示关系。如果把这个向量变成坐标轴，再根据以上变化矩阵计算出新的坐标轴的位置，放在转换矩阵中，可以得到rot_new_to_old。没错是，new_to_old，因为是把新的坐标轴的基向量在原坐标系下的值放进去的。

还是按照z->y->x的旋转顺序，可以一次得到(1,0,0),(0,1,0),(0,0,1)旋转后分别是：

 ===》新的x坐标轴在原坐标系的表示

 ===》新的y坐标轴在原坐标系的表示

 ===》新的z坐标轴在原坐标系的表示。

构建一个Rot3x3矩阵，把这三列，放进去，就得到了Rot_new_to_old矩阵：

 

回到标题的问题，坐标轴旋转后，原来的向量是在新的坐标系怎么表示呢？

就是这样了，取个逆，得到Rot_old_to_new，再乘上原来的向量，就得到了在新坐标系下的表示。

3、利用这些信息来计算静止状态下的imu的roll、pitch角度

目标是求出，imu的坐标系，相对于Enu坐标系的转换，即Rot_body_to_enu。

已知道在imu下测量到的重力情况为：grav_body=[acc_x,acc_y,acc_z]，这个在body坐标系下；

在Enu坐标系下，grav_enu重力的情况为：[0,0,-g] （重力方向向下，enu的z轴向上）。

按照上面的说法，R_new_to_old，可以直接获取，利用关系计算：

grav_enu=R_new_to_old*grav_body

得到：

0=gx=cp*cy*ax-cp*sy*ay+sp*az

0=(cr*sy+sr*sp*cy)*ax+(cr*cy-sr*sp*sy)*ay+sr*cp*az

-g=(sr*sy-cr*sp*cy)*ax+(sr*cy+cr*sp*sy)*ay+cr*cp*az

这个不是很好算。

转换一下思路：

以grav_body为开始坐标，计算grav_enu相对于它的旋转情况，那就比较简单:

grav_body(当做是old) = R_new_to_old * grav_enu(当做是new) 

算出这个R_new_to_old后，求个逆，就得到了 grav_body->grav_enu的变化。

因为grav_enu 中的x\y都是0，所以可以得：

ax=sp*gz

ay=-sr*cp*gz

az=cr*cp*gz

那么：pitch=asin(ax/gz) roll=-atan(ay/az)

将角度带入那个R_new_to_old（这里的new、old都是相对来说的，哪个都可以作为new和old），就可以得到这个rot矩阵。此时的含义是env_to_body。

求逆以后，得到body_to_env，再获里面的roll、pitch，就是body相对于enu旋转的角度。

（会不会太绕了，起码思路清晰连贯了）

Eigen::Matrix3d calc_rot_body_to_enu(Eigen::Vector3d grav_in_old,Eigen::Vector3d grav_in_body){
    
    Eigen::Vector3d acc_mea_in_body=grav_in_body;
    // std::cout<<"grav_in_old = "<